text
stringlengths 1
7.94M
| lang
stringclasses 5
values |
|---|---|
Women of color remain underrepresented in technology and leadership, to the detriment of employers and the economy. IT executive Monica Eaton-Cardone explains how greater diversity can translate to financial and business advantages.
By 2060, women of color will account for over half of the U.S. female population; yet they hold just 11% of all science and engineering jobs, 10% of mid-level managerial positions, 5% of senior and executive management positions, and 4% of board seats.(1) Monica Eaton-Cardone, an IT executive specializing in risk management and fraud prevention, says this disparity harms businesses and the economy. She notes that research findings(2–9) make a strong case for the economic and competitive advantages of supporting multicultural women in technology and business.
Eaton-Cardone advises employers to review the research demonstrating the economic and business advantages of diversity, and to look to industry leaders for best practices in hiring, retaining and promoting women and minorities. She also urges women of color to explore the many programs and nonprofit groups that have emerged in recent years—including Women of Color in Computing(2)—and to leverage these resources in their ongoing push for greater representation in the workplace.
Monica Eaton-Cardone frequently discusses financial technology (FinTech) advances and opportunities for women in technology and business at industry conferences and events. She has been a featured panelist at TRUSTECH, the IATA World Financial Symposium and TRANSACT, and is also available for interviews and future speaking engagements. For more information, visit http://monicaec.com.
Monica Eaton-Cardone is an accomplished entrepreneur, speaker, author and industry thought leader who is internationally recognized for her expertise in risk management, chargeback mitigation, fraud prevention and merchant education. Eaton-Cardone found her calling as an entrepreneur when she sold her first business at the age of 19. She later became an eCommerce merchant; and after grappling with chargebacks and fraud, she took it upon herself to develop a comprehensive, robust solution that combined agile technologies and human insights. Today, Eaton-Cardone’s innovations are helping thousands of organizations achieve sustainable growth, and she continues to pioneer loss-prevention best practices as CIO of Global Risk Technologies and COO of Chargebacks911. Eaton-Cardone is a champion of women in IT and business leadership, and aims to inspire the next generation of young innovators through her nonprofit organization, Get Paid for Grades. Get to know her at http://www.monicaec.com.
1. Catalyst. Quick Take: Women of Color in the United States; October 12, 2017.
2. McAlear, Frieda; Allison Scott; et al. Data Brief: Women of Color in Computing; August 2018.
3. Herring, Cedric. “Does Diversity Pay?: Race, Gender, and the Business Case for Diversity”; American Sociological Review; April 1, 2009.
4. Hunt, Vivian; Lareina Yee; et al. Delivering Through Diversity; McKinsey & Company report; January 2018.
5. Noland, Marcus; Tyler Moran; and Barbara Kotschwar. Is Gender Diversity Profitable? Evidence From a Global Survey; Peterson Institute for International Economics report; February 2016.
6. PricewaterhouseCoopers. PwC Women in Work Index: Closing the Gender Pay Gap; March 2018.
7. The Nielsen Company. African-American Women: Our Science, Her Magic; September 21, 2017.
8. American Express OPEN. The 2017 State of Women-Owned Businesses Report; November 8, 2017.
9. Johnson, Emily. “IT Pros Are More Equipped to Address Diversity Than You’d Think”; InformationWeek; May 3, 2018. | english |
IJ_BCautoMacro
==============
ImageJ Automatic Brightness & Contrast Enhancement in ImageJ macro
"Auto" button in the brightness and contrast interface and the contrast enhancement provided in the menu as "Process > Enhance Contrast" use different algorithms. This macro mimics the algorithm used for the former enhancement.
See the link below:
<http://imagej.1557.x6.nabble.com/Auto-Brightness-Contrast-and-setMinAndMax-td4968628.html>
May 16th, 2012 Version 1.0
- Author: Damien Guimond & Kota Miura
- Contact: miura@embl.de
- Lisence: GNU General Public License, version 2
- <http://www.gnu.org/licenses/old-licenses/gpl-2.0.en.html>
| code |
\begin{document}
\author{Valentin Gutev}
\address{Department of Mathematics, Faculty of Science, University of
Malta, Msida MSD 2080, Malta}
\email{valentin.gutev@um.edu.mt}
\subjclass[2010]{54C60, 54C65, 54D20, 54F45, 55M10, 55U10}
\keywords{Lower locally constant mapping, continuous selection,
connectedness in finite dimension, $C$-space, finite $C$-space,
finite-dimensional space, simplicial complex, nerve.}
\title[Constructing Selections Stepwise Over Cones]{Constructing
Selections Stepwise Over Cones of Simplicial Complexes}
\begin{abstract}
It is obtained a natural generalisation of Uspenskij's selection
characterisation of paracompact $C$-spaces. The method developed to
achieve this result is also applied to give a simplified proof of a
similar characterisation of paracompact finite $C$-space obtained
previously by Valov. Another application is a characterisation of
finite-dimensional paracompact spaces which generalises both a
remark done by Michael and a result obtained by the author.
\end{abstract}
\date{\today}
\maketitle
\section{Introduction}
All spaces in this paper are Hausdorff topological spaces. A space $X$
has property $C$, or is a \emph{$C$-space}, \label{page-c-space}
if for any sequence $\{\mathscr{U} _n:n<\omega\}$ of open covers of
$X$ there exists a sequence $\{\mathscr{V} _n:n<\omega\}$ of open
pairwise-disjoint families in $X$ such that each $\mathscr{V} _n$
refines $\mathscr{U} _n$ and $\bigcup_{n<\omega}\mathscr{V} _n$ is a
cover of $X$. The $C$-space property was originally defined by W.\
Haver \cite{haver:1974} for compact metric spaces, subsequently Addis
and Gresham \cite{addis-gresham:78} reformulated Haver's definition
for arbitrary spaces. It should be remarked that a $C$-space $X$ is
paracompact if and only if it is countably paracompact and normal, see
e.g.\ \cite[Proposition 1.3]{MR2352366}. Every finite-dimensional
paracompact space, as well as every countable-dimensional metrizable
space, is a $C$-space \cite{addis-gresham:78}, but there exists a
compact metric $C$-space which is not countable-dimensional
\cite{pol:81}.
In what follows, we will use $\Phi:X\sto Y$ to designate that $\Phi$
is a map from $X$ to the nonempty subsets of $Y$, i.e.\ a
\emph{set-valued mapping}. A map $f:X\to Y$ is a \emph{selection} for
$\Phi:X\sto Y$ if $f(x)\in \Phi(x)$, for all $x\in X$. A mapping
$\Phi:X\sto Y$ is \emph{lower locally constant}, see \cite{gutev:05},
if the set $\{x\in X:K\subset \Phi(x)\}$ is open in $X$, for every
compact subset $K\subset Y$. This property appeared in a paper of
Uspenskij \cite{uspenskij:98}; later on, it was used by some authors
(see, for instance, \cite{chigogidze-valov:00a,valov:00}) under the
name ``strongly l.s.c.'', while in papers of other authors strongly
l.s.c.\ was already used for a different property of set-valued
mappings (see, for instance, \cite{gutev:95e}). Regarding our
terminology, let us remark that a singleton-valued mapping (i.e.\ a
usual map) is lower locally constant precisely when it is locally
constant.
Finally, let us recall that a space $S$ is \emph{aspherical} if every
continuous map of the $k$-sphere ($k\geq 0$) in $S$ can be extended to
a continuous map of the $(k+1)$-ball in $S$. The following theorem
was obtained by Uspenskij \cite[Theorem 1.3]{uspenskij:98}.
\begin{theorem}[\cite{uspenskij:98}]
\label{theorem-Select-Ext-v6:1}
A paracompact space $X$ is a $C$-space if and only if for every
topological space $Y$, each lower locally constant aspherical-valued
mapping $\Phi : X\sto Y$ has a continuous selection.
\end{theorem}
For $k\ge 0$ and subsets $S, B\subset Y$, we will write that
$S\embed{k} B$ if every continuous map of the $k$-sphere in $S$ can be
extended to a continuous map of the $(k+1)$-ball in $B$. Similarly,
for mappings $\varphi, \psi :X\sto Y$, we will write
$\varphi \embed{k}\psi$ to express that $\varphi(x)\embed{k}\psi(x)$,
for every $x\in X$. In these terms, we shall say that a sequence of
mappings $\varphi_n: X\sto Y$, $n<\omega$, is \emph{aspherical} if
$\varphi_n\embed{n}\varphi_{n+1}$, for every $n<\omega$. Also, to each
sequence of mappings $\varphi_n:X\sto Y$, $n<\omega$, we will
associate its union $\bigcup_{n<\omega}\varphi_n:X\sto Y$, defined
pointwise by
$\left[\bigcup_{n<\omega}\varphi_n\right]
(x)=\bigcup_{n<\omega}\varphi_n(x)$, $x\in X$.
In the present paper, we will show that the mapping $\Phi:X\sto Y$ in
Theorem~\ref{theorem-Select-Ext-v6:1} can be replaced by an aspherical
sequence of lower locally constant mappings $\varphi_n:X\sto Y$,
$n<\omega$. Namely, the following theorem will be proved.
\begin{theorem}
\label{theorem-Select-Ext-v6:2}
A paracompact space $X$ is a $C$-space if and only if for every
topological space $Y$, each aspherical sequence $\varphi_n:X\sto Y$,
$n<\omega$, of lower locally constant mappings admits a continuous
selection for its union $\bigcup_{n<\omega}\varphi_n$.
\end{theorem}
By taking $\varphi_n=\varphi_{n+1}$, $n<\omega$, the selection
property in Theorem \ref{theorem-Select-Ext-v6:2} immedia\-tely
implies that of Theorem \ref{theorem-Select-Ext-v6:1}. Implicitly, the
selection property in Theorem~\ref{theorem-Select-Ext-v6:1} also
implies that of Theorem \ref{theorem-Select-Ext-v6:2} because both
these properties are equivalent to $X$ being a $C$-space. However,
the author is not aware of any explicit argument show\-ing this. In this
regard and in contrast to Theorem \ref{theorem-Select-Ext-v6:1}, the
proof of Theorem~\ref{theorem-Select-Ext-v6:2} is straightforward
in both directions. Here is briefly the idea behind this
proof.
In the next section, we deal with a simple construction of continuous
extensions of maps over cones of simplicial complexes, see Proposition
\ref{proposition-Select-Ext-v3:1}. This construction is applied in
Section \ref{sec:skeletal-selections} to special simplicial complexes
which are defined in Section \ref{sec:finite-asph-sequ}. Namely, in
Section \ref{sec:finite-asph-sequ}, to each cover
$\bigcup_{n<\omega} \mathscr{U}_n$ of $X$ consisting of families
$\mathscr{U}_n$, $n<\omega$, of subsets of $X$, we associate a
subcomplex $\Delta(\mathscr{U}_{<\omega})$ of the nerve
$\mathscr{N}(\mathscr{U}_{<\omega})$, where $\mathscr{U}_{<\omega}$
stands for the disjoint union $\bigsqcup_{n<\omega}\mathscr{U}_n$, see
Example~\ref{example-Select-Ext-v12:1}. Intuitively,
$\Delta(\mathscr{U}_{<\omega})$ consists of those simplices
$\sigma\in \mathscr{N}(\mathscr{U}_{<\omega})$ which have at most one
vertex in each $\mathscr{U}_n$, $n<\omega$. One benefit of this
subcomplex is that
$\Delta(\mathscr{V}_{<\omega})= \mathscr{N}(\mathscr{V}_{<\omega})$,
whenever the families $\mathscr{V}_n$, $n<\omega$, are as in the
defining property of $C$-spaces, i.e.\ pairwise-disjoint, see
Proposition \ref{proposition-Select-Ext-v16:3}. Another benefit is
that each sequence of covers $\mathscr{U}_n$, $n<\omega$, of $X$
generates a natural aspherical sequence of mappings on $X$. This is
done by considering the sequence of subcomplexes
$\Delta(\mathscr{U}_{\leq n})$, $n<\omega$, where each
$\Delta(\mathscr{U}_{\leq n})$ is defined as above with respect to the
indexed cover $\mathscr{U}_{\leq n}=\bigsqcup_{k=0}^n \mathscr{U}_k$
of $X$. Then each $\Delta(\mathscr{U}_{\leq n})$, $n<\omega$,
generates a simplicial-valued mapping
$\Delta_{[\mathscr{U}_{\leq n}]}:X\sto \Delta(\mathscr{U}_{\leq n})$
which assigns to each $x\in X$ the simplicial complex
$\Delta_{[\mathscr{U}_{\leq n}]}(x)$ of those simplices
$\sigma\in \Delta(\mathscr{U}_{\leq n})$ for which
$x\in \bigcap\sigma$. Finally, we consider the geometric realisation
$\left|\Delta(\mathscr{U}_{\leq n})\right|$ of
$\Delta(\mathscr{U}_{\leq n})$ and the set-valued mapping
$\left|\Delta_{[\mathscr{U}_{\leq n}]}\right|:X\sto
\left|\Delta(\mathscr{U}_{\leq n})\right|\subset
\left|\Delta(\mathscr{U}_{<\omega})\right|$ corresponding to the
``geometric realisation'' of $\Delta_{[\mathscr{U }_{\leq n}]}$.
Thus, for open locally finite covers $\mathscr{U}_n$, ${n<\omega}$, of
$X$, the sequence
$\left|\Delta_{[\mathscr{U}_{\leq n}]}\right|:X\sto
\left|\Delta(\mathscr{U}_{<\omega})\right|$, $n<\omega$, is always
aspherical and consists of lower locally constant mappings,
Propositions \ref{proposition-Select-Ext-v16:1} and
\ref{proposition-Select-Ext-v16:2}. In Section
\ref{sec:skeletal-selections}, by restricting $X$ to be a paracompact
space, we show that each aspherical sequence $\varphi_n:X\sto Y$,
$n<\omega$, of lower locally constant mappings admits a sequence
$\mathscr{F}_n$, $n<\omega$, of closed locally finite interior covers
of $X$ and a continuous map
$f:\left|\Delta(\mathscr{F}_{<\omega})\right|\to Y$ such that each
composite mapping
${f\circ \left|\Delta_{[\mathscr{F}_{\leq n}]}\right|:X\sto Y}$ is a
set-valued selection for $\varphi_n$, $n<\omega$, see Theorem
\ref{theorem-Select-Ext-v14:1}. This is applied in
Section~\ref{sec:select-canon-maps} to show that the selection problem
in Theorem \ref{theorem-Select-Ext-v6:2} is now equivalent to that of
the mappings
$\left|\Delta_{[\mathscr{U}_{\leq n}]}\right|:X\sto
\left|\Delta(\mathscr{U}_{<\omega})\right|$, $n<\omega$, corresponding
to open locally finite covers $\mathscr{U}_n$, $n<\omega$, of $X$,
Theorem \ref{theorem-Select-Ext-vgg-rev:1}. In the same section, this
selection problem is further reduced to the existence of canonical
maps $f:X\to \left|\Delta(\mathscr{U}_{<\omega})\right|$, Corollary
\ref{corollary-Select-Ext-v22:1}. Finally, in Section
\ref{sec:canon-maps-sequ}, it is shown that the existence of canonical
maps $f:X\to \left|\Delta(\mathscr{U}_{<\omega})\right|$ is equivalent
to $C$-like properties of $X$, Theorem
\ref{theorem-Select-Ext-v18:2}. Theorem \ref{theorem-Select-Ext-v6:2}
is then obtained as a special case of Theorem
\ref{theorem-Select-Ext-v18:2}, see Corollary
\ref{corollary-Select-Ext-v18:1}. Here, let us explicitly remark that
two other special cases of Theorem \ref{theorem-Select-Ext-v18:2} are
covering two other similar results --- Corollary
\ref{corollary-Select-Ext-v18:2} (a selection theorem of Valov
\cite[Theorem 1.1]{valov:00} about finite $C$-spaces) and Corollary
\ref{corollary-Select-Ext-v18:3} (generalising both a remark done by
Michael in \cite[Remark 2]{uspenskij:98} and a result obtained by the
author in \cite[Theorem~3.1]{gutev:2018a}).
\section{Extensions of maps over cones of simplicial complexes}
\label{sec:extensions-maps-over}
By a \emph{simplicial complex} we mean a collection $\Sigma$ of
nonempty finite subsets of a set $S$ such that $\tau\in \Sigma$,
whenever $\varnothing\neq \tau\subset \sigma\in \Sigma$. The set
$\bigcup\Sigma $ is the \emph{vertex set} of $\Sigma$, while each
element of $\Sigma$ is called a \emph{simplex}. The
\emph{$k$-skeleton} $\Sigma^k$ of $\Sigma$ ($k\geq 0$) is the
simplicial complex
$\Sigma^{k}=\{\sigma\in \Sigma:\card(\sigma)\leq k+1\}$, where
$\card(\sigma)$ is the cardinality of $\sigma$. In the sequel, for
simplicity, we will identify the vertex set of $\Sigma$ with its
$0$-skeleton $\Sigma^0$, and will say that $\Sigma$ is a
\emph{$k$-dimensional} if $\Sigma=\Sigma^k$.
The vertex set $\Sigma^0$ of each simplicial complex $\Sigma$ can be
embedded as a linearly independent subset of some linear normed
space. Then to any simplex $\sigma\in \Sigma$, we may associate the
corresponding \emph{geometric simplex} $|\sigma|$ which is the
convex hull of $\sigma$. Thus, $\card(\sigma)=k+1$ if and only if
$|\sigma|$ is a \emph{$k$-dimensional simplex}. Finally, we set
$|\Sigma|=\bigcup\{|\sigma|:\sigma\in \Sigma\}$ which is called the
\emph{geometric realisation} of $\Sigma$. As a topological space, we
will always consider $|\Sigma|$ endowed with the \emph{Whitehead
topology} \cite{MR1576810,MR0030759}. This is the topology in which
a subset $U\subset |\Sigma|$ is open if and only if $U\cap |\sigma|$
is open in $|\sigma|$, for every $\sigma\in \Sigma$.
The \emph{cone} $Z*v$ over a space $Z$ with a vertex $v$ is the
quotient space of $Z\times[0,1]$ obtained by identifying all points of
$Z\times\{1\}$ into a single point $v$. For a simplicial complex
$\Sigma$ and a point $v$ with $v\notin \Sigma^0$, the \emph{cone} on
$\Sigma$ with a vertex $v$ is the simplicial complex defined by
\[
\Sigma*v=\Sigma\cup\left\{\sigma\cup \{v\}:
\sigma\in\Sigma\right\}\cup \{\{v\}\}.
\]
Evidently, we have that $|\Sigma|*v=|\Sigma*v|$.
\begin{proposition}
\label{proposition-Select-Ext-v3:1}
Let ${S_0,\dots,S_{n+1}\subset Y}$ with
${\varnothing\neq S_0\embed{0} S_1\embed{1} \cdots \embed{n}
S_{n+1}}$, and $g:|\Sigma|\to S_n$ be a continuous map from an
$n$-dimensional simplicial complex $\Sigma$ such that
$g(|\Sigma^k|)\subset S_k$, for every $k\leq n$. If
$v\notin \Sigma^0$, then $g$ can be extended to a continuous map
$h:|\Sigma*v|\to S_{n+1}$ such that $h(|(\Sigma*v)^k|)\subset S_k$,
for every $k\leq n+1$.
\end{proposition}
\begin{proof}
By a finite induction, extend each restriction
$g_k=g\uhr\left|\Sigma^k\right|$ to a continuous map
${h_k:\left|(\Sigma*v)^k\right|\to S_k}$, $k\leq n$, such that
$h_k\uhr \left|(\Sigma*v)^{k-1}\right|=h_{k-1}$, $k>0$. Briefly,
define $h_0:(\Sigma*v)^0\to S_0$ by $h_0\uhr \Sigma^0= g_0$ and
$h_0(v)\in S_0$. Whenever $u\in \Sigma^0$ is a vertex of $\Sigma$,
the map $h_0:\{u,v\}\to S_0$ can be extended to a continuous map
$h_{(1,u)}:|\{u,v\}|\to S_1$ because $S_0\embed{0} S_1$. Then the
map $h_1:\left|(\Sigma*v)^1\right|\to S_1$ defined by
$h_1\uhr (\Sigma*v)^0=h_0$, $h_1\uhr |\Sigma^1|=g_1$ and
$h_1\uhr |\{u,v\}|=h_{(1,u)}$, $u\in \Sigma^0$, is a continuous
extension of both $h_0$ and $g_1$. The construction can be carried
on by induction to get a continuous extension
$h_n:|(\Sigma*v)^n|\to S_n$ of $g=g_n$ with the required
properties. Finally, if $\sigma\in \Sigma*v$ is an
$(n+1)$-dimensional simplex, then $h_n$ is defined on the boundary
$|\sigma|\cap |(\Sigma*v)^n|$ of $|\sigma|$ which is homeomorphic to
the $n$-sphere. Hence, it can be extended to a continuous map
$h_\sigma:|\sigma|\to S_{n+1}$ because $S_n\embed{n} S_{n+1}$. The
required map $h:|\Sigma*v|\to S_{n+1}$ is now defined by
$h\uhr |(\Sigma*v)^n|=h_n$ and $h\uhr |\sigma|=h_\sigma$, for every
$(n+1)$-dimensional simplex $\sigma\in \Sigma*v$.
\end{proof}
\section{Nerves of sequences of covers}
\label{sec:finite-asph-sequ}
The set $\Sigma_S$ of all nonempty finite subsets of a set $S$ is a
simplicial complex. Another natural example is the \emph{nerve} of an
indexed cover $\{U_\alpha:\alpha\in \mathscr{A}\}$ of a
set $X$, which is the subcomplex of $\Sigma_\mathscr{A}$ defined by
\begin{equation}
\label{eq:Select-Ext-v1:1}
\mathscr{N}(\mathscr{A})= \left\{\sigma\in
\Sigma_\mathscr{A}:\bigcap_{\alpha\in
\sigma}U_\alpha\neq\varnothing\right\}.
\end{equation}
Following Lefschetz \cite{MR0007093}, the intersection
$\bigcap_{\alpha\in \sigma}U_\alpha$ is called the \emph{kernel} of
$\sigma$, and is often denoted by $\ker[\sigma]=\bigcap_{\alpha\in
\sigma}U_\alpha$. In case $\mathscr{U}$ is an unindexed cover of
$X$, its nerve is denoted by $\mathscr{N}(\mathscr{U})$. In this case,
$\mathscr{U}$ is indexed by itself, and each simplex $\sigma\in
\mathscr{N}(\mathscr{U})$ is merely a nonempty finite subset of
$\mathscr{U}$ with $\ker[\sigma]=\bigcap \sigma\neq
\varnothing$.
Here, an important role will be played by a subcomplex of the nerve of
a special indexed cover of $X$. The prototype of this subcomplex can be
found in some of the considerations in the proof of
\cite[Theorem 2.1]{uspenskij:98}.
\begin{example}
\label{example-Select-Ext-v12:1}
Whenever $0<\kappa\leq \omega$, let $\mathscr{U}_n$, $n<\kappa$, be
families of subsets of $X$ such that
$\bigcup_{n<\kappa}\mathscr{U}_n$ is a cover of $X$, and let
$\bigsqcup_{n<\kappa}\mathscr{U}_n$ be the \emph{disjoint union} of
these families (obtained, for instance, by identifying each
$\mathscr{U}_n$ with $\mathscr{U}_n\times\{n\}$, $n<\kappa$). The
nerve of this indexed cover of $X$ defines a natural simplicial
complex
\begin{equation}
\label{eq:Select-Ext-v12:2}
\mathscr{N}\left(\mathscr{U}_{<\kappa}\right)=
\mathscr{N}\left(\bigsqcup_{n<\kappa}\mathscr{U}_n\right).
\end{equation}
A simplex $\sigma\in \mathscr{N}(\mathscr{U}_{<\kappa})$ can be
described as the disjoint union $\sigma=\bigsqcup_{i=1}^m \sigma_i$
of finitely many simplices
$\sigma_i\in \mathscr{N}(\mathscr{U}_{n_i})$,
for $n_1<\dots <n_m<\kappa$, such that
$\bigcap_{i=1}^m \ker[\sigma_i]\neq \varnothing$. The simplicial
complex $\mathscr{N}(\mathscr{U}_{<\kappa})$ contains a natural
subcomplex $\Delta(\mathscr{U}_{<\kappa})$, define by
\begin{equation}
\label{eq:Select-Ext-v12:4}
\Delta(\mathscr{U}_{<\kappa})=\big\{\sigma\in
\mathscr{N}(\mathscr{U}_{<\kappa}):
\card(\sigma\cap \mathscr{U}_n\times\{n\})\leq 1,\
n<\kappa\big\}.
\end{equation}
In other words, the subcomplex $\Delta(\mathscr{U}_{<\kappa})$
consists of those simplices
$\sigma\in \mathscr{N}\left(\mathscr{U}_{<\kappa}\right)$ which are
composed of finitely many vertices
$U_i=(U_{i},n_i)\in \mathscr{U}_{n_i}$, $i\leq m$, where
$n_1<\dots <n_m<\kappa$. In the special case of $\kappa=n+1<\omega$,
we will simply write
$\mathscr{N}(\mathscr{U}_{\leq
n})=\mathscr{N}(\mathscr{U}_{<\kappa})$ and
$\Delta(\mathscr{U}_{\leq n})=\Delta(\mathscr{U}_{<\kappa})$.\qed
\end{example}
The subcomplex $\Delta(\mathscr{U}_{<\kappa})$ in Example
\ref{example-Select-Ext-v12:1} is naturally related to the definition
of $C$-spaces. The following proposition is an immediate consequence
of \eqref{eq:Select-Ext-v12:4}.
\begin{proposition}
\label{proposition-Select-Ext-v16:3}
Let $0<\kappa\leq \omega$ and $\mathscr{V}_n$, $n<\kappa$, be a
sequence of pairwise-disjoint families of subsets of $X$, whose
union forms a cover of $X$. Then
\begin{equation}
\label{eq:Select-Ext-v12:3}
\Delta(\mathscr{V}_{<\kappa})=\mathscr{N}(\mathscr{V}_{<\kappa}).
\end{equation}
\end{proposition}
For a simplicial complex $\Sigma$, a mapping $\Omega:X\sto \Sigma$
will be called \emph{simplicial-valued} if $\Omega(p)$ is a subcomplex
of $\Sigma$, for each $p\in X$. Such a mapping $\Omega:X\sto \Sigma$
generates a mapping $|\Omega|:X\sto |\Sigma|$ defined by
\begin{equation}
\label{eq:Select-Ext-v16:2}
|\Omega|(p)=\left|\Omega(p)\right|= \bigcup_{\sigma\in
\Omega(p)}|\sigma|,\quad p\in X.
\end{equation}
Here is a natural example. Each indexed cover
$\{U_\alpha:\alpha\in \mathscr{A}\}$ of $X$ generates a natural
simplicial-valued mapping
$\Sigma_\mathscr{A}:X\sto \Sigma_\mathscr{A}$, defined by
\begin{equation}
\label{eq:Select-Ext-v15:2}
\Sigma_\mathscr{A}(p)=\left\{\sigma\in \Sigma_\mathscr{A}:
p\in\bigcap_{\alpha\in
\sigma}U_\alpha\right\}, \quad p\in X.
\end{equation}
In fact, each $\Sigma_\mathscr{A}(p)$ is a subcomplex of
$\mathscr{N}(\mathscr{A})$, so
$\Sigma_\mathscr{A}:X\sto \mathscr{N}(\mathscr{A})$.
The benefit of the mapping in \eqref{eq:Select-Ext-v15:2} comes in the
setting of the simplicial complex $\Delta(\mathscr{U}_{<\kappa})$ in
Example \ref{example-Select-Ext-v12:1} associated to a sequence of
covers $\mathscr{U}_n$, $n<\kappa$, of $X$ for some
$0<\kappa\leq \omega$. Namely, we may define the corresponding
simplicial-valued mapping
$\Delta_{[\mathscr{U}_{<\kappa}]}:X\sto \Delta(\mathscr{U}_{<\kappa})$
by the same pattern as in \eqref{eq:Select-Ext-v15:2}, i.e.
\begin{equation}
\label{eq:Select-Ext-v15:3}
\Delta_{[\mathscr{U}_{<\kappa}]}(p)= \big\{\sigma\in
\Delta(\mathscr{U}_{<\kappa}):
p\in\ker[\sigma]\big\}, \quad p\in X.
\end{equation}
Just like before, we will write
$\Delta_{[\mathscr{U}_{\leq n}]}=\Delta_{[\mathscr{U}_{<\kappa}]}$
whenever $\kappa=n+1<\omega$.
We now have the following natural relationship with aspherical
sequences of lower locally constant mappings.
\begin{proposition}
\label{proposition-Select-Ext-v16:1}
Let $\mathscr{U}_n$, $n<\omega$, be a sequence of covers of a set
$X$. Then
\begin{equation}
\label{eq:Select-Ext-v16:1}
\Delta_{[\mathscr{U}_{\leq n}]}(p)*U\subset \Delta_{[\mathscr{U}_{\leq
n+1}]}(p), \quad\text{whenever $p\in U\in \mathscr{U}_{n+1}$ and
$n<\omega$.}
\end{equation}
Accordingly,
$\left|\Delta_{[\mathscr{U}_{\leq n}]}\right|:X\sto
|\Delta(\mathscr{U}_{\leq n})|\subset
|\Delta(\mathscr{U}_{<\omega})|$, $n<\omega$, is an aspherical
sequence of mappings.
\end{proposition}
\begin{proof}
The property in \eqref{eq:Select-Ext-v16:1} follows from the fact
that $U=(U,n+1)\notin \bigsqcup_{k=0}^n\mathscr{U}_k$, whenever
$p\in U\in \mathscr{U}_{n+1}$. Since
$\left|\Delta_{[\mathscr{U}_{\leq
n}]}(p)*U\right|=\left|\Delta_{[\mathscr{U}_{\leq
n}]}(p)\right|*U$ is contractible, this implies that
$\left|\Delta_{[\mathscr{U}_{\leq n}]}(p)\right|\embed{n} \left|
\Delta_{[\mathscr{U}_{\leq n}]}(p)*U\right| \subset
\left|\Delta_{[\mathscr{U}_{\leq n+1}]}(p)\right|$.
\end{proof}
\begin{proposition}
\label{proposition-Select-Ext-v16:2}
Let $\mathscr{U}_0,\dots, \mathscr{U}_n$ be a sequence of
point-finite open covers of a space $X$. Then the mapping
$\left|\Delta_{[\mathscr{U}_{\leq n}]}\right|:X\sto
|\Delta(\mathscr{U}_{\leq n})|$ is lower locally constant.
\end{proposition}
\begin{proof}
Whenever $p\in X$, the set
$V_p=\bigcap\left\{U\in \bigcup_{k\leq n}\mathscr{U}_k:
p\in U\right\}$ is a neighbourhood of $p$. Take a point
$q\in V_p$. Then by \eqref{eq:Select-Ext-v15:3},
$\sigma\in \Delta_{[\mathscr{U}_{\leq n}]}(p)$ implies that
$\sigma\in \Delta_{[\mathscr{U}_{\leq n}]}(q)$ because $q\in
V_p\subset \ker[\sigma]$. Thus,
$\Delta_{[\mathscr{U}_{\leq n}]}(p)\subset
\Delta_{[\mathscr{U}_{\leq n}]}(q)$ and, accordingly,
$\left|\Delta_{[\mathscr{U}_{\leq n}]}\right|$ is lower locally
constant.
\end{proof}
We conclude this section with a remark about the importance of
disjoint unions in the definition of the subcomplex
$\Delta(\mathscr{U}_{<\kappa})$ in Example
\ref{example-Select-Ext-v12:1}.
\begin{remark}
\label{remark-Select-Ext-v19:1}
For a sequence of covers $\mathscr{U}_n$, $n<\kappa$, of $X$, where
$0<\kappa\leq \omega$, one can define the subcomplex
$\Delta(\mathscr{U}_{<\kappa})\subset
\mathscr{N}(\mathscr{U}_{<\kappa})$ by considering
$\mathscr{N}(\mathscr{U}_{<\kappa})$ to be the nerve of the usual
unindexed cover $\bigcup_{n<\kappa}\mathscr{U}_n$, rather than the
disjoint union $\bigsqcup_{n<\kappa}\mathscr{U}_n$. However, this
will not work to establish a property similar to that in Proposition
\ref{proposition-Select-Ext-v16:1}, also for the essential results
in the next sections (see, for instance, Theorem
\ref{theorem-Select-Ext-v14:1} and Lemma
\ref{lemma-Select-Ext-v4:1}). Namely, suppose that $\mathscr{U}_0$
and $\mathscr{U}_1$ are covers of $X$ which contain elements
$U_i\in \mathscr{U}_i$, $i=0,1$, with $U_0\cap U_1\neq \varnothing$
and $U_i\notin \mathscr{U}_{1-i}$. Then
$\sigma=\{U_0,U_1\}\in \Delta(\mathscr{U}_{\leq 1})$. However, if
$\mathscr{U}_2$ is a cover of $X$ with $U_0,U_1\in \mathscr{U}_2$,
and $\Delta(\mathscr{U}_{\leq 2})$ is defined on the basis of
unindexed covers, then
$\Delta(\mathscr{U}_{\leq 1})\not\subset \Delta(\mathscr{U}_{\leq
2})$ because
$\sigma=\{U_0,U_1\}\notin \Delta(\mathscr{U}_{\leq
2})$. \qed
\end{remark}
\section{Skeletal selections}
\label{sec:skeletal-selections}
For mappings $\varphi,\psi:X\sto Y$, we will write
$\varphi\subset \psi$ to express that $\varphi(p)\subset \psi(p)$, for
every $p\in X$. In this case, the mapping $\varphi$ is called a
\emph{set-valued selection}, or a \emph{multi-selection}, for
$\psi$. Also, let us recall that a cover $\mathscr{F}$ of a space $X$
is called \emph{interior} if the collection of the interiors of the
elements of $\mathscr{F}$ is a cover of $X$.
The following theorem will be proved in this section.
\begin{theorem}
\label{theorem-Select-Ext-v14:1}
Let $X$ be a paracompact space and $\varphi_n:X\sto Y$, $n<\omega$,
be an aspherical sequence of lower locally constant mappings in a
space $Y$. Then there exists a sequence $\mathscr{F}_n$, $n<\omega$,
of closed locally finite interior covers of $X$ and a continuous map
${f:\big|\Delta(\mathscr{F}_{<\omega})\big|\to Y}$ such that
\begin{equation}
\label{eq:Select-Ext-v14:1}
f\circ \left|\Delta_{[\mathscr{F}_{\leq n}]}\right|\subset
\varphi_n,\quad \text{for every $n<\omega$.}
\end{equation}
\end{theorem}
Let us explicitly remark that, here,
$\Delta_{[\mathscr{F}_{\leq n}]}:X\sto \Delta(\mathscr{F}_{\leq
n})\subset \Delta(\mathscr{F}_{<\omega})$
is the simplicial-valued mapping associated to the covers
$\mathscr{F}_k$, $k\leq n$, see \eqref{eq:Select-Ext-v15:3}, while
$f\circ \left|\Delta_{[\mathscr{F}_{\leq n}]}\right|$ is the composite
mapping
\begin{center}
\begin{tikzcd}
&&\lvert\Delta(\mathscr{F}_{<\omega})\rvert \arrow[d, "f"]\\
{X} \arrow[urr, rightsquigarrow,
"\left\lvert\Delta_{\skobi{\mathscr{F}_{\leq n}}}\right\rvert", bend left=15]
\arrow[rr, rightsquigarrow, "f\circ
\left\lvert\Delta_{\skobi{\mathscr{F}_{\leq n}}} \right\rvert"] &&
Y
\end{tikzcd}
\end{center}
According to the definition of
$\Delta_{[\mathscr{F}_{\leq n}]}:X\sto \Delta(\mathscr{F}_{\leq n})$,
see also \eqref{eq:Select-Ext-v16:2}, the property in
\eqref{eq:Select-Ext-v14:1} means that
$f(|\sigma|) \subset \varphi_n(p)$, for every
$\sigma \in \Delta(\mathscr{F}_{\leq n})$ and
$p\in\ker[\sigma]$.
Turning to the proof of Theorem \ref{theorem-Select-Ext-v14:1}, let us
observe that the simplicial complex $\Delta(\mathscr{F}_{\leq n})$ is
$n$-dimensional, see \eqref{eq:Select-Ext-v12:4} of Example
\ref{example-Select-Ext-v12:1}. In what follows, its $k$-skeleton will
be denoted by $\Delta^k(\mathscr{F}_{\leq n})$. In these terms,
following the idea of an $n$-skeletal selection in \cite{gutev:2018a},
we shall say that a continuous map
$f:|\Delta(\mathscr{F}_{\leq n})|\to Y$ is a \emph{skeletal selection}
for a sequence of mappings $\varphi_0,\dots,\varphi_n:X\sto Y$ if
\begin{equation}
\label{eq:Select-Ext-v4:3}
f(|\sigma|) \subset \varphi_k(p),\ \text{for every $\sigma \in
\Delta^k(\mathscr{F}_{\leq n})$,
$k\leq n$, and $p\in\ker[\sigma]$.}
\end{equation}
Precisely as in \eqref{eq:Select-Ext-v15:3}, for each $k\leq n$ we may
associate the simplicial-valued mapping
$\Delta^k_{[\mathscr{F}_{\leq n}]}:X\sto \Delta^k(\mathscr{F}_{\leq
n})$, which assigns to each $p$ in $ X$ the $k$-skeleton
$\Delta^k_{[\mathscr{F}_{\leq n}]}(p)$ of the subcomplex
$\Delta_{[\mathscr{F}_{\leq n}]}(p)\subset \Delta(\mathscr{F}_{\leq
n})$. Then the property in \eqref{eq:Select-Ext-v4:3} means that the
composite mapping
$f\circ \left|\Delta^k_{[\mathscr{F}_{\leq n}]}\right|:X\sto
\left|\Delta^k(\mathscr{F}_{\leq n})\right|$ is a set-valued selection
for $\varphi_k$, for every $k\leq n$.
Finally, let us recall that a \emph{simplicial map}
$g:\Sigma_1\to \Sigma_2$ is a map $g:\Sigma_1^0\to \Sigma_2^0$ between
the vertices of simplicial complexes $\Sigma_1$ and $\Sigma_2$ such
that $g(\sigma)\in \Sigma_2$, for each $\sigma\in \Sigma_1$. If such a
map $g:\Sigma_1^0\to \Sigma_2^0$ is bijective, then the inverse
$g^{-1}$ is also a simplicial map, and we say that $g$ is a
\emph{simplicial isomorphism}. If $g$ is only injective, then $g$
embeds $\Sigma_1$ into $\Sigma_2$, so that we may consider $\Sigma_1$
as a subcomplex of $\Sigma_2$. Each simplicial map
$g:\Sigma_1\to \Sigma_2$ generates a continuous map
$|g|:|\Sigma_1|\to |\Sigma_2|$ which is affine on each geometric
simplex $|\sigma|$, for $\sigma\in \Sigma_1$.
\begin{lemma}
\label{lemma-Select-Ext-v4:1}
Let $Y$ be a space, $\mathscr{F}_0,\dots,\mathscr{F}_{n}$ be a
sequence of closed locally finite covers of a paracompact space $X$,
and $\varphi_0,\dots, \varphi_{n+1}:X\sto Y$ be a sequence of lower
locally constant mappings with $\varphi_k \embed{k}\varphi_{k+1}$
for every $k\leq n$. If ${f_n:|\Delta(\mathscr{F}_{\leq n})|\to Y}$
is a skeletal selection for $\varphi_0,\dots,\varphi_n$, then there
exists a closed locally finite interior cover $\mathscr{F}_{n+1}$ of
$X$ and a continuous extension
$f_{n+1}:|\Delta(\mathscr{F}_{\leq n+1})|\to Y$ of $f_n$ which is a
skeletal selection for $\varphi_0,\dots,\varphi_{n+1}$.
\end{lemma}
\begin{proof}
Let
$\Delta_{[\mathscr{F}_{\leq n}]}:X\sto \Delta(\mathscr{F}_{\leq n})$
be the associated simplicial-valued mapping, defined as in
\eqref{eq:Select-Ext-v15:3}. Whenever $p\in X$, the subcomplex
\begin{equation}
\label{eq:Select-Ext-v16:3}
\Delta_p=\Delta_{[\mathscr{F}_{\leq n}]}(p)
\end{equation}
is $n$-dimensional such that, by \eqref{eq:Select-Ext-v4:3},
$f_n\left(\left|\Delta^k_p\right|\right)\subset \varphi_k(p)$,
$k\leq n$. Moreover, by hy\-pothesis,
$\varphi_k(p) \embed{k}\varphi_{k+1}(p)$ for every $k\leq n$. Since
$p\notin \Delta_p^0$, it follows from Proposition
\ref{proposition-Select-Ext-v3:1} that $f_n\uhr |\Delta_p|$ can be
extended to a continuous map ${f_p:|\Delta_p* p|\to Y}$ such that
\begin{equation}
\label{eq:Select-Ext-v2:2}
f_p\left(\left|(\Delta_p*
p)^k\right|\right)\subset
\varphi_k(p),\quad \text{for every
$0\leq k\leq n+1$.}
\end{equation}
Since all covers are locally finite and closed, the point
$p\in X$ is contained in the open set
\begin{equation}
\label{eq:Select-Ext-v3:2}
O_p=X\setminus \bigcup\left\{F\in \mathscr{F}_0\cup\dots
\cup\mathscr{F}_n: p\notin F\right\}.
\end{equation}
For the same reason, $\Delta_p*p$ is a finite simplicial
complex. Accordingly, each set
$f_p\left(\left|(\Delta_p*p)^k\right|\right)$, $k\leq n+1$, is
compact. Hence, by \eqref{eq:Select-Ext-v2:2} and the hypothesis
that each mapping $\varphi_k$, $k\leq n+1$, is lower locally
constant, we may shrink $O_p$ to a neighbourhood $V_p$ of $p$,
defined by
\begin{equation}
\label{eq:Select-Ext-v1:3}
V_{p}= \left\{x\in O_p:
f_p\left(\left|(\Delta_p*p)^k\right|\right)\subset
\varphi_k(x),\ \text{for every $k\leq n+1$}\right\}.
\end{equation}
Finally, since $X$ is paracompact, it has an open locally finite
cover $\mathscr{U}_{n+1}$ such that $\{V_{p}: p\in X\}$ is refined
by the associated cover
$\mathscr{F}_{n+1}=\left\{\overline{U}: U\in
\mathscr{U}_{n+1}\right\}$ of the closures of the elements of
$\mathscr{U}_{n+1}$. So, there is a map $p:\mathscr{F}_{n+1}\to X$
such that
\begin{equation}
\label{eq:st-app-vgg-rev:4}
F\subset V_{p(F)}\subset O_{p(F)},\quad \text{for every $F\in
\mathscr{F}_{n+1}$.}
\end{equation}
Having already defined the cover $\mathscr{F}_{n+1}$, we are going
to extend $f_n$ to a skeletal selection
$f_{n+1}:\big|\Delta(\mathscr{F}_{\leq n+1})\big|\to Y$ for the
sequence $\varphi_0,\dots,\varphi_{n+1}$. To this end, take an
$F\in \mathscr{F}_{n+1}$, and define the set
\[
\Delta_F=\big\{\tau\in \Delta(\mathscr{F}_{\leq n}):
\tau\cup\{F\}\in \Delta(\mathscr{F}_{\leq n+1})\big\}.
\]
It is evident that $\Delta_F$ is a subcomplex of
$\Delta(\mathscr{F}_{\leq n})$ with $F\notin \Delta_F^0$, hence the
cone $\Delta_F*F$ is a subcomplex of
$\Delta(\mathscr{F}_{\leq n+1})$. Thus, to extend $f_n$ to a
skeletal selection
$f_{n+1}:\big|\Delta(\mathscr{F}_{\leq n+1})\big|\to Y$ for the
sequence $\varphi_0,\dots,\varphi_{n+1}$, it now suffices to extend
each $f_n\uhr |\Delta_F|$, $F\in \mathscr{F}_{n+1}$, to a continuous
map $f_F:|\Delta_F*F|\to Y$ satisfying the condition in
\eqref{eq:Select-Ext-v4:3} with respect to the simplices of
$\Delta_F*F$. To this end, let us observe that
\begin{equation}
\label{eq:Select-Ext-v3:3}
\Delta_F\subset \Delta_{p(F)}=\Delta_{[\mathscr{F}_{\leq n}]}(p(F)).
\end{equation}
Indeed, for $T\in\tau\in \Delta_F$, we have that
$\varnothing\neq T\cap F\subset T\cap O_{p(F)}$, see
\eqref{eq:st-app-vgg-rev:4}. Hence, by \eqref{eq:Select-Ext-v3:2},
$p(F)\in T$ and according to \eqref{eq:Select-Ext-v15:3} and
\eqref{eq:Select-Ext-v16:3}, $\tau\in \Delta_{p(F)}$.
We are now ready to define the required maps
$f_F:|\Delta_F*F|\to Y$, $F\in \mathscr{F}_{n+1}$. Namely, by
\eqref{eq:Select-Ext-v3:3}, we can embed $\Delta_{F}*F$ into the
cone $\Delta_{p(F)}*p(F)$ by identifying $p(F)$ with $F$. Let
$\ell:\Delta_F*F\to \Delta_{p(F)}*p(F)$ be the corresponding
simplicial embedding defined by $\ell\uhr \Delta^0_F$ to be the
identity of $\Delta^0_F$, and $\ell(F)=p(F)$. Next, define a
continuous extension $f_F:|\Delta_F*F|\to Y$ of $f_n\uhr |\Delta_F|$
by $f_F=f_{p(F)}\circ |\ell|$. Take a simplex
$\sigma\in (\Delta_F*F)^k$ for some $k\leq n+1$, and a point
$x\in \ker[ \sigma]$. If $\sigma\in \Delta_F$, by the properties of
$f_n$, see \eqref{eq:Select-Ext-v4:3},
$f_F(|\sigma|)=f_n(|\sigma|)\subset \varphi_k(x)$. If $F\in \sigma$,
then $x\in F\subset V_{p(F)}$ and, by \eqref{eq:Select-Ext-v1:3}, we
have again that
$f_F(|\sigma|)= f_{p(F)}(|\ell|(|\sigma|)) \subset
\varphi_k(x)$. The proof is complete.
\end{proof}
Complementary to Lemma \ref{lemma-Select-Ext-v4:1} is the following
well-known property, see the proof of \cite[Theorem 2.1]{uspenskij:98}
and that of \cite[Theorem 3.1]{gutev:05}. The property itself was
stated explicitly in \cite[Proposition 3.2]{gutev:2018a}, and is an
immediate consequence of the definition of lower locally constant
mappings.
\begin{proposition}
\label{proposition-Select-Ext-v4:1}
If $X$ is a paracompact space and $\varphi:X\sto Y$ is a lower
locally constant mapping, then there exists a closed locally finite
interior cover $\mathscr{F}$ of $X$ and a
\textup{(}continuous\textup{)} map
$f:\Delta(\mathscr{F})=\mathscr{F}\to Y$ such that
$f(F)\in \varphi(x)$, for every $x\in F\in \mathscr{F}$.
\end{proposition}
\begin{proof}[Proof of Theorem \ref{theorem-Select-Ext-v14:1}]
Inductively, using Proposition \ref{proposition-Select-Ext-v4:1} and
Lemma \ref{lemma-Select-Ext-v4:1}, there exists a sequence
$\mathscr{F}_n$, $n<\omega$, of closed locally finite interior
covers of $X$ and continuous maps
$f_n:\big|\Delta(\mathscr{F}_{\leq n})\big|\to Y$, $n<\omega$, such
that each $f_n$ is a skeletal selection for the sequence
$\varphi_0,\dots,\varphi_n$, and each $f_{n+1}$ is an extension of
$f_n$. Since
$\Delta(\mathscr{F}_{<\omega})=\bigcup_{n<\omega}
\Delta(\mathscr{F}_{\leq n})$, we may define a map
$f:\big|\Delta(\mathscr{F}_{<\omega})\big|\to Y$ by
$f\uhr \big|\Delta(\mathscr{F}_{\leq n})\big|= f_n$, for every
$n<\omega$. Then $f$ is continuous and clearly has the property in
\eqref{eq:Select-Ext-v14:1}.
\end{proof}
\section{Selections and canonical maps}
\label{sec:select-canon-maps}
Suppose that $X$ is a (paracompact) space with the property that for
any space $Y$, each aspherical sequence $\varphi_n:X\sto Y$,
$n<\omega$, of lower locally constant mappings admits a continuous
selection for its union $\bigcup_{n<\omega}\varphi_n$. As we will see
in the next section (Corollaries \ref{corollary-Select-Ext-v18:1},
\ref{corollary-Select-Ext-v18:2} and \ref{corollary-Select-Ext-v18:3}
and Example \ref{example-Select-Ext-v18:1}), each one of the following
statements determines a different dimension-like property of
$X$.
\begin{enumerate}[label=\upshape{(\thesection.\arabic*)}]
\item\label{item:Select-Ext-v18:1} There exists an aspherical sequence
$\varphi_n:X\sto Y$, $n<\omega$, of lower locally constant mappings
such that no $\varphi_n$, $n<\omega$, has a continuous
selection.
\item\label{item:Select-Ext-v18:2} For each aspherical sequence
$\varphi_k:X\sto Y$, $k<\omega$, of lower locally constant mappings
there exists an $n<\omega$ such that $\varphi_n$ has a continuous
selection.
\item\label{item:Select-Ext-v18:3} There exists an $n<\omega$ such
that for each aspherical sequence $\varphi_k:X\sto Y$, $k<\omega$,
of lower locally constant mappings, the mapping $\varphi_n$ has a
continuous selection.
\end{enumerate}
Here, we deal with the following general result reducing these
selection problems only to simpli\-cial-valued mappings associated to
open locally finite covers of $X$.
\begin{theorem}
\label{theorem-Select-Ext-vgg-rev:1}
For a space $Y$, a paracompact space $X$ and $0<\mu\leq \omega+1$,
the following are equivalent\textup{:}
\begin{enumerate}
\item\label{item:Select-Ext-v14:1} If $\varphi_n:X\sto Y$,
$n<\omega$, is an aspherical sequence of lower locally constant
mappings, then $\bigcup_{n<\kappa}\varphi_n$ has a
continuous selection for some $0<\kappa<\mu$.
\item\label{item:Select-Ext-v14:2} If $\mathscr{U}_n$, $n<\omega$,
is a sequence of open locally finite covers of $X$, then
${\left|\Delta_{[\mathscr{U}_{<\kappa}]}\right|:X\sto
\big|\Delta(\mathscr{U}_{<\kappa}) \big|}$ has a continuous
selection for some $0<\kappa<\mu$.
\end{enumerate}
\end{theorem}
The proof of Theorem \ref{theorem-Select-Ext-vgg-rev:1} is based on
the results of the previous two sections and the following
observation.
\begin{proposition}
\label{proposition-Select-Ext-v21:1}
Let $\mathscr{U}_n$, $n<\omega$, be a sequence of covers of $X$,
$0<\kappa\leq \omega$, and $\mathscr{V}_n$, $n<\kappa$, be a sequence of
families of subsets of $X$ such that each $\mathscr{V}_n$ refines
$\mathscr{U}_n$ and $\bigcup_{n<\kappa}\mathscr{V}_n$ is a cover of
$X$. If\/ $\left|\Delta_{[\mathscr{V}_{<\kappa}]}\right|:X\sto
\left|\Delta(\mathscr{V}_{<\kappa})\right|$ has a continuous selection,
then so does $\left|\Delta_{[\mathscr{U}_{<\kappa}]}\right|:X\sto
\left|\Delta(\mathscr{U}_{<\kappa})\right|$.
\end{proposition}
\begin{proof}
Since each $\mathscr{V}_n$ refines $\mathscr{U}_n$, there are maps
$r_n:\mathscr{V}_n\to \mathscr{U}_n$, $n<\kappa$, such that
$V\subset r_n(V)$, for all $V\in \mathscr{V}_n$. Accordingly,
$r=\bigsqcup_{n<\kappa}r_n:\Delta(\mathscr{V}_{<\kappa})\to
\Delta(\mathscr{U}_{<\kappa})$ is a simplicial map with the property
that $\sigma\subset r(\sigma)$, for each simplex
$\sigma\in \Delta(\mathscr{V}_{<\kappa})$. In other words,
$r\circ \Delta_{[\mathscr{V}_{<\kappa}]}\subset
\Delta_{[\mathscr{U}_{<\kappa}]}$, see \eqref{eq:Select-Ext-v15:3}, and
therefore
$|r|\circ \left|\Delta_{[\mathscr{V}_{<\kappa}]}\right|\subset
\left|\Delta_{[\mathscr{U}_{<\kappa}]}\right|$. Thus, if
$h:X\to \left|\Delta(\mathscr{V}_{<\kappa})\right|$ is a continuous
selection for
$\left|\Delta_{[\mathscr{V}_{<\kappa}]}\right|:X\sto
\left|\Delta(\mathscr{V}_{<\kappa})\right|$, then the composite map
$f= |r|\circ h:X\to \left|\Delta(\mathscr{U}_{<\kappa})\right|$ is a
continuous selection for
$\left|\Delta_{[\mathscr{U}_{<\kappa}]}\right|:X\sto
\left|\Delta(\mathscr{U}_{<\kappa})\right|$.
\end{proof}
\begin{proof}[Proof of Theorem \ref{theorem-Select-Ext-vgg-rev:1}]
The implication
\ref{item:Select-Ext-v14:1}$\implies$\ref{item:Select-Ext-v14:2}
follows from Propositions \ref{proposition-Select-Ext-v16:1} and
\ref{proposition-Select-Ext-v16:2}. The converse follows easily from
Theorem \ref{theorem-Select-Ext-v14:1} and Proposition
\ref{proposition-Select-Ext-v21:1}. Namely, assume that
\ref{item:Select-Ext-v14:2} holds and $\varphi_n:X\sto Y$,
$n<\omega$, is as in \ref{item:Select-Ext-v14:1}. Since $X$ is
paracompact, by Theorem \ref{theorem-Select-Ext-v14:1}, there exists
a sequence $\mathscr{F}_n$, $n<\omega$, of closed locally finite
interior covers of $X$ and a continuous map
$f:\big|\Delta_{[\mathscr{F}_{<\omega}]}\big|\to Y$ satisfying
\eqref{eq:Select-Ext-v14:1}. For each $n<\omega$, let
$\mathscr{U}_n$ be the cover of $X$ composed by the interiors of the
elements of $\mathscr{F}_n$. Then by \ref{item:Select-Ext-v14:2},
the mapping
$\left|\Delta_{[\mathscr{U}_{<\kappa}]}\right|:X\sto
\big|\Delta(\mathscr{U}_{<\kappa}) \big|$ has a continuous selection
for some $0<\kappa<\mu$. According to Proposition
\ref{proposition-Select-Ext-v21:1}, this implies that the mapping
$\left|\Delta_{[\mathscr{F}_{<\kappa}]}\right|:X\sto
\left|\Delta(\mathscr{F}_{<\kappa})\right|$ also has a continuous
selection $h:X\to \big|\Delta(\mathscr{F}_{<\kappa}) \big|$. Evidently,
the composite map $g=f\circ h:X\to Y$ is a continuous selection for
the mapping $\bigcup_{n<\kappa}\varphi_n$.
\end{proof}
The selection problem in \ref{item:Select-Ext-v14:2} of Theorem
\ref{theorem-Select-Ext-vgg-rev:1} is naturally related to the
existence of canonical maps for the disjoint union
$\bigsqcup_{n<\kappa}\mathscr{U}_n$ of such covers. To this end, let us
briefly recall some terminology. For a simplicial complex $\Sigma$
and a simplex $\sigma\in \Sigma$, we use $\langle\sigma\rangle$ to
denote the \emph{relative interior} of the geometric simplex
$|\sigma|$. For a vertex $v\in \Sigma^0$, the set
\setcounter{equation}{3}
\begin{equation}
\label{eq:Select-Ext-v7:4}
\st\langle v\rangle
=\bigcup_{v\in \sigma\in \Sigma}\langle\sigma\rangle,
\end{equation}
is called the \emph{open star} of the vertex $v\in \Sigma^0$. One can
easily see that $\st\langle v\rangle$ is open in $|\Sigma|$ because
$\st\langle v\rangle=|\Sigma|\setminus\bigcup_{v\notin \sigma\in
\Sigma}|\sigma|$. In these terms, for an indexed cover
$\{U_\alpha:\alpha\in \mathscr{A}\}$ of a space $X$, a continuous map
$f:X\to |\mathscr{N}(\mathscr{A})|$ is called \emph{canonical} for
$\{U_\alpha:\alpha\in \mathscr{A}\}$ if
\begin{equation}
\label{eq:Select-Ext-v7:1}
f^{-1}(\st\langle \alpha\rangle)\subset U_\alpha,\quad \text{for
every $\alpha\in
\mathscr{A}$.}
\end{equation}
It is well known that each open cover of a paracompact space admits a
canonical map, which follows from the fact that such a cover has an
index-subordinated partition of unity. The interested reader is
referred to \cite[Section 2]{gutev:2018a} which contains a brief
review of several facts about canonical maps and partitions of unity.
Here, we are interested in a selection interpretation of canonical
maps. Namely, in terms of the simplicial-valued mapping
$\Sigma_\mathscr{A}:X\sto \mathscr{N}(\mathscr{A})$ associated to the
cover $\{U_\alpha:\alpha\in \mathscr{A}\}$, see
\eqref{eq:Select-Ext-v15:2}, we have the following characterisation of
canonical maps; for unindexed covers it was obtained in
\cite[Proposition 2.5]{gutev:2018a} (see also Dowker
\cite{dowker:47}), but the proof for indexed covers is essentially the
same.
\begin{proposition}
\label{proposition-Select-Ext-v11:1}
A map $f:X\to |\mathscr{N}(\mathscr{A})|$ is canonical for a cover
$\{U_\alpha:\alpha\in \mathscr{A}\}$ of a space $X$ if and only if
it is a continuous selection for the associated mapping
$|\Sigma_\mathscr{A}|:X\sto |\mathscr{N}(\mathscr{A})|$.
\end{proposition}
In the special case of a sequence of open covers $\mathscr{U}_n$,
$n<\omega$, a canonical map
$f:X\to \mathscr{N}(\mathscr{U}_{<\omega})$ for the disjoint union
$\bigsqcup_{n<\omega}\mathscr{U}_n$ will be called \emph{canonical}
for the sequence $\mathscr{U}_n$, $n<\omega$. We now have the
following further reduction of the selection problem for aspherical
sequences of mappings, which is an immediate consequence of Theorem
\ref{theorem-Select-Ext-vgg-rev:1} and Proposition
\ref{proposition-Select-Ext-v11:1}.
\begin{corollary}
\label{corollary-Select-Ext-v22:1}
For a space $Y$, a paracompact space $X$ and $0<\mu\leq \omega+1$,
the following are equivalent\textup{:}
\begin{enumerate}
\item\label{item:Select-Ext-v18:4} If $\varphi_n:X\sto Y$,
$n<\omega$, is an aspherical sequence of lower locally constant
mappings, then $\bigcup_{n<\kappa}\varphi_n$ has a
continuous selection for some $0<\kappa<\mu$.
\item\label{item:Select-Ext-v18:5} Each sequence $\mathscr{U}_n$,
$n<\omega$, of open covers of $X$ admits a canonical map
$f:X\to \big|\Delta(\mathscr{U}_{<\kappa}) \big|\subset
\left|\mathscr{N}(\mathscr{U}_{<\omega})\right|$ for some
$0<\kappa<\mu$.
\end{enumerate}
\end{corollary}
\section{Dimension and canonical maps}
\label{sec:canon-maps-sequ}
Here, we finalise the proof of Theorem \ref{theorem-Select-Ext-v6:2}
by showing that the property $C$ is equivalent to the existence of
canonical maps for special covers. To this end, for a sequence
$\mathscr{U}_n$, $n<\omega$, of open covers of $X$ and
$0<\kappa\leq \omega$, we shall say that a sequence $\mathscr{V}_n$,
$n<\kappa$, of pairwise-disjoint families of open subsets $X$ is a
\emph{$C$-refinement} of $\mathscr{U}_n$, $n<\omega$, if each family
$\mathscr{V}_n$ refines $\mathscr{U}_n$ and
$\bigcup_{n<\kappa}\mathscr{V}_n$ covers $X$.
\begin{theorem}
\label{theorem-Select-Ext-v18:2}
For a paracompact space $X$ and $0<\mu\leq \omega+1$, the following
are equivalent\textup{:}
\begin{enumerate}
\item\label{item:Select-Ext-v18:6} Each sequence $\mathscr{U}_n$,
$n<\omega$, of open covers of $X$ has a $C$-refinement
$\mathscr{V}_n$, $n<\kappa$, for some $0<\kappa<\mu$.
\item\label{item:Select-Ext-v18:7} Each sequence $\mathscr{U}_n$,
$n<\omega$, of open covers of $X$ admits a canonical map
$f:X\to \big|\Delta(\mathscr{U}_{<\kappa}) \big|$ for some
$0<\kappa<\mu$.
\end{enumerate}
\end{theorem}
\begin{proof}
To see that
\ref{item:Select-Ext-v18:6}$\implies$\ref{item:Select-Ext-v18:7},
take a sequence $\mathscr{U}_n$, $n<\omega$, of open covers of
$X$. Then by \ref{item:Select-Ext-v18:6}, $\mathscr{U}_n$,
$n<\omega$, admits a $C$-refinement $\mathscr{V}_n$, $n<\kappa$, for
some $0<\kappa<\mu$. Let $\mathscr{N}(\mathscr{V}_{<\kappa})$ be
the nerve of the disjoint union $\bigsqcup_{n<\kappa}\mathscr{V}_n$,
see \eqref{eq:Select-Ext-v12:2} of
Example~\ref{example-Select-Ext-v12:1}, and
$\Sigma_{[\mathscr{V}_{<\kappa}]}:X\sto
\mathscr{N}(\mathscr{V}_{<\kappa})$ be the simplicial-valued mapping
associated to this nerve, see \eqref{eq:Select-Ext-v15:2}. Since
$X$ is paracompact, the indexed cover
$\bigsqcup_{n<\kappa}\mathscr{V}_n$ has a canonical map. Hence, by
Proposition \ref{proposition-Select-Ext-v11:1}, the mapping
$\left|\Sigma_{[\mathscr{V}_{<\kappa}]}\right|:X\sto
\left|\mathscr{N}(\mathscr{V}_{<\kappa})\right|$ has a continuous
selection. However, by definition, each family $\mathscr{V}_n$,
$n<\kappa$, is pairwise-disjoint. Therefore, by
\eqref{eq:Select-Ext-v12:3} of Proposition
\ref{proposition-Select-Ext-v16:3},
$\Delta(\mathscr{V}_{<\kappa})=\mathscr{N}(\mathscr{V}_{<\kappa})$
and, consequently,
$\Delta_{[\mathscr{V}_{<\kappa}]}=\Sigma_{[\mathscr{V}_{<\kappa}]}$. Thus,
$\left|\Delta_{[\mathscr{V}_{<\kappa}]}\right|:X\sto
\left|\Delta(\mathscr{V}_{<\kappa})\right|$ has a continuous
selection and, according to Proposition
\ref{proposition-Select-Ext-v21:1}, the mapping
$\left|\Delta_{[\mathscr{U}_{<\kappa}]}\right|:X\sto
\left|\Delta(\mathscr{U}_{<\kappa})\right|$ has a continuous
selection as well. Finally, by Proposition
\ref{proposition-Select-Ext-v11:1}, each continuous selection for
$\left|\Delta_{[\mathscr{U}_{<\kappa}]}\right|$ is as required in
\ref{item:Select-Ext-v18:7}.
Conversely, let $\mathscr{U}_n$, $n<\omega$, and
${f:X\to \left|\Delta(\mathscr{U}_{<\kappa})\right|}$ be as in
\ref{item:Select-Ext-v18:7} for some ${0<\kappa<\mu}$. Define
$\mathscr{V}_n=\left\{f^{-1}(\st\langle U\rangle): U\in
\mathscr{U}_n\right\}$, $n<\kappa$. Since $f$ is continuous,
$\mathscr{V}_n$ is an open family in $X$; moreover, by
\eqref{eq:Select-Ext-v7:1}, it refines $\mathscr{U}_n$. It is also
evident that $\bigcup_{n<\mu}\mathscr{V}_n$ covers $X$, see
\eqref{eq:Select-Ext-v7:4}. We complete the proof by showing that
$\mathscr{V}_n$ is pairwise-disjoint as well. To this end, suppose
that
$p\in f^{-1}(\st\langle U_1\rangle)\cap f^{-1}(\st\langle
U_2\rangle)$ for some $U_1,U_2\in \mathscr{U}_n$ and $p\in X$. Then
$f(p)\in \st\langle U_1\rangle\cap \st\langle U_2\rangle$ and by
\eqref{eq:Select-Ext-v7:4}, we have that
$f(p)\in \langle\sigma_1\rangle\cap \langle\sigma_2\rangle$ for some
simplices $\sigma_1,\sigma_2\in \Delta(\mathscr{U}_{<\kappa})$ with
$U_i\in \sigma_i$, $i=1,2$. Since the collection
$\left\{\langle \sigma\rangle: \sigma\in
\Delta(\mathscr{U}_{<\kappa})\right\}$ forms a partition of
$\left|\Delta(\mathscr{U}_{<\kappa})\right|$, this implies that
$\sigma_1=\sigma_2$. Finally, according to the definition of
$\Delta(\mathscr{U}_{<\mu})$, see \eqref{eq:Select-Ext-v12:4}, we
get that $U_1=U_2$. Thus, each family $\mathscr{V}_n$, $n<\mu$, is
also pairwise-disjoint, and the proof is complete.
\end{proof}
We finalise the paper with several applications. The first one is the
following slight generalisation of Theorem
\ref{theorem-Select-Ext-v6:2}; it is an immediate consequence of
Corollary~\ref{corollary-Select-Ext-v22:1} and Theorem
\ref{theorem-Select-Ext-v18:2} (in the special case of
$\mu=\omega+1$).
\begin{corollary}
\label{corollary-Select-Ext-v18:1}
For a paracompact space $X$, the following are equivalent\textup{:}
\begin{enumerate}
\item\label{item:Select-Ext-v7:1} $X$ is a $C$-space.
\item\label{item:Select-Ext-v7:2} For every space $Y$, each
aspherical sequence $\varphi_n : X\sto Y$, $n<\omega$, of lower
locally constant mappings admits a continuous selection for its
union $\bigcup_{n<\omega} \varphi_n$.
\item\label{item:Select-Ext-v7:3} Each sequence $\mathscr{U}_n$,
$n<\omega$, of open covers of $X$ admits a canonical map
$f:X\to \big|\Delta(\mathscr{U}_{<\omega})\big|$.
\end{enumerate}
\end{corollary}
Another consequence is for the case when $0<\mu=\omega$, and deals
with the so called finite $C$-spaces. These spaces were defined by
Borst for separable metrizable spaces, see \cite{MR2280911};
subsequently, the definition was extended by Valov \cite{valov:00} for
arbitrary spaces. For simplicity, we will consider these spaces in the
realm of normal spaces. In this setting, a (normal) space $X$ is
called a \emph{finite $C$-space} if for any sequence
$\{\mathscr{U} _k:k<\omega\}$ of finite open covers of $X$ there
exists a finite sequence $\{\mathscr{V} _k:k\leq n\}$ of open
pairwise-disjoint families in $X$ such that each $\mathscr{V} _k$
refines $\mathscr{U} _k$ and $\bigcup_{k\leq n}\mathscr{V} _k$ is a
cover of $X$. It was shown by Valov in \cite[Theorem 2.4]{valov:00}
that a paracompact space $X$ is a finite $C$-space if and only if each
sequence $\{\mathscr{U} _k:k<\omega\}$ of open covers of $X$ admits a
finite $C$-refinement, i.e.\ there exists a finite sequence
$\{\mathscr{V} _k:k\leq n\}$ of open pairwise-disjoint families in $X$
such that each $\mathscr{V} _k$ refines $\mathscr{U} _k$ and
$\bigcup_{k\leq n}\mathscr{V} _k$ is a cover of $X$. Based on this, we
have the following consequence of Corollary
\ref{corollary-Select-Ext-v22:1} and Theorem
\ref{theorem-Select-Ext-v18:2} (in the special case of $\mu=\omega$).
\begin{corollary}
\label{corollary-Select-Ext-v18:2}
For a paracompact space $X$, the following are equivalent\textup{:}
\begin{enumerate}
\item\label{item:Select-Ext-v12:1} $X$ is a finite $C$-space.
\item\label{item:Select-Ext-v12:2} For each aspherical sequence
$\varphi_k : X\sto Y$, $k<\omega$, of lower locally constant
mappings in a space $Y$, there exists $n<\omega$ such that
$\varphi_n$ has a continuous selection.
\item\label{item:Select-Ext-v12:3} Each sequence $\mathscr{U}_k$,
$k<\omega$, of open covers of $X$ admits a canonical map
$f:X\to \big|\Delta(\mathscr{U}_{\leq n})\big|$ for some
$n<\omega$.
\end{enumerate}
\end{corollary}
Let us explicitly remark that the equivalence
\ref{item:Select-Ext-v12:1}$\iff$\ref{item:Select-Ext-v12:2} in
Corollary \ref{corollary-Select-Ext-v18:2} was obtained by Valov in
\cite[Theorem 1.1]{valov:00}. His arguments were following those in
\cite{uspenskij:98} for proving Theorem \ref{theorem-Select-Ext-v6:1}.
Accordingly, our approach is providing a simplification of this
proof. Regarding the proper place of finite $C$-spaces, it was shown
by Valov in \cite[Proposition 2.2]{valov:00} that a Tychonoff space
$X$ is a finite $C$-space if and only if its \v{C}ech-Stone
compactification $\beta X$ is a $C$-space. This brings a natural
distinction between the selection problems stated in
\ref{item:Select-Ext-v18:1} and \ref{item:Select-Ext-v18:2}.
\begin{example}
\label{example-Select-Ext-v18:1}
The following example of a $C$-space which is not finite $C$ was
given in \cite[Remark 3.7]{MR2080284}. Let $K_\omega$ be the
subspace of the Hilbert cube $[0,1]^\omega$ consisting of all points
which have only finitely many nonzero coordinates. Then $K_\omega$
is a $C$-space being strongly countable-dimensional, but is not a
finite $C$-space because each compactification of $K_\omega$
contains a copy of $[0,1]^\omega$ (as per \cite[Example
5.5.(1)]{MR722011}). According to Corollaries
\ref{corollary-Select-Ext-v18:1} and
\ref{corollary-Select-Ext-v18:2}, see also Theorem
\ref{theorem-Select-Ext-vgg-rev:1}, this implies that there exists a
space $Y$ and an aspherical sequence $\varphi_n:K_\omega\sto Y$,
$n<\omega$, of lower locally constant mappings such that
$\bigcup_{n<\omega}\varphi_n$ has a continuous selection, but none
of the mappings $\varphi_n$, $n<\omega$, has a continuous
selection.\qed
\end{example}
Our last application is for the case when $\mu=n+1$ for some
$n<\omega$. To this end, following \cite{gutev:2018a}, a finite
sequence $\varphi_k:X\sto Y$, $0\leq k\leq n$, of mappings will be
called \emph{aspherical} if $\varphi_k\embed{k} \varphi_{k+1}$, for
every $k<n$. By letting $\varphi_k(p)=Y*q$ be the cone on $Y$ with a
fixed vertex $q$, where $p\in X$ and $k>n$, each finite aspherical
sequence $\varphi_k:X\sto Y$, $0\leq k\leq n$, can be extended to an
aspherical sequence $\varphi_k:X\sto Y*q$, $k<\omega$. Furthermore, in
this construction, each resulting new mapping $\varphi_k$, $k>n$, is
lower locally constant being a constant set-valued mapping.
Regarding dimension properties of the domain, let us recall a result
of Ostrand \cite{ostrand:71} that for a normal space $X$ with a
covering dimension $\dim(X)\leq n$, each open locally finite cover
$\mathscr{U}$ of $X$ admits a sequence
$\mathscr{V}_0, \dots, \mathscr{V}_n$ of open pairwise-disjoint
families such that each $\mathscr{V}_k$ refines $\mathscr{U}_k$ and
$\bigcup_{k=0}^n\mathscr{V}_k$ covers $X$. This result was refined by
Addis and Gresham, see \cite[Proposition 2.12]{addis-gresham:78}, that
a paracompact space $X$ has a covering dimension $\dim(X)\leq n$ if
and only if each finite sequence $\mathscr{U}_0,\dots, \mathscr{U}_n$
of open covers of $X$ has a finite $C$-refinement, i.e.\ there exists
a finite sequence $\mathscr{V}_0,\dots, \mathscr{V}_n$ of open
pairwise-disjoint families of $X$ such that each $\mathscr{V}_k$
refines $\mathscr{U}_k$ and $\bigcup_{k=0}^n \mathscr{V}_k$ covers
$X$. Just like before, setting $\mathscr{U}_k=\mathscr{U}_n$, $k>n$,
the above characterisation of the covering dimension of paracompact
spaces remains valid for an infinite sequence $\mathscr{U}_k$,
$k<\omega$, of open covers of $X$. Accordingly, we also have the
following consequence of Corollary \ref{corollary-Select-Ext-v22:1}
and Theorem \ref{theorem-Select-Ext-v18:2} (in the special case of
$\mu=n+1<\omega$).
\begin{corollary}
\label{corollary-Select-Ext-v18:3}
For a paracompact space $X$, the following are equivalent\textup{:}
\begin{enumerate}
\item\label{item:Select-Ext-v18:8} $\dim(X)\leq n$.
\item\label{item:Select-Ext-v18:9} For each aspherical sequence
$\varphi_k : X\sto Y$, $0\leq k\leq n$, of lower locally
constant mappings in a space $Y$, the mapping $\varphi_n$ has
a continuous selection.
\item\label{item:Select-Ext-v18:10} Each sequence $\mathscr{U}_k$,
$0\leq k\leq n$, of open covers of $X$ admits a canonical map
$f:X\to \big|\Delta(\mathscr{U}_{\leq n})\big|$.
\end{enumerate}
\end{corollary}
A direct poof of the implication
\ref{item:Select-Ext-v18:8}$\implies$\ref{item:Select-Ext-v18:9} in
Corollary \ref{corollary-Select-Ext-v18:3} was given in \cite[Theorem
3.1]{gutev:2018a}. Let us also remark that in the special case when
all mappings $\varphi_k$, $0\leq k\leq n$, are equal, the equivalence
of \ref{item:Select-Ext-v18:8} and \ref{item:Select-Ext-v18:9} in
Corollary \ref{corollary-Select-Ext-v18:3} was shown in \cite[Remark
2]{uspenskij:98} and credited to Ernest Michael.
\providecommand{\bysame}{\leavevmode\hbox to3em{\hrulefill}\thinspace}
\end{document} | math |
<?php if ( ! defined('BASEPATH')) exit('No direct script access allowed');
/*
* LimeSurvey
* Copyright (C) 2007-2012 The LimeSurvey Project Team / Carsten Schmitz
* All rights reserved.
* License: GNU/GPL License v2 or later, see LICENSE.php
* LimeSurvey is free software. This version may have been modified pursuant
* to the GNU General Public License, and as distributed it includes or
* is derivative of works licensed under the GNU General Public License or
* other free or open source software licenses.
* See COPYRIGHT.php for copyright notices and details.
*/
function loadanswers()
{
Yii::trace('start', 'survey.loadanswers');
global $surveyid;
global $thissurvey, $thisstep;
global $clienttoken;
$scid=Yii::app()->request->getQuery('scid');
if (Yii::app()->request->getParam('loadall') == "reload")
{
$sLoadName=Yii::app()->request->getParam('loadname');
$sLoadPass=Yii::app()->request->getParam('loadpass');
$oCriteria= new CDbCriteria;
$oCriteria->join="LEFT JOIN {{saved_control}} ON t.id={{saved_control}}.srid";
$oCriteria->condition="{{saved_control}}.sid=:sid";
$aParams=array(':sid'=>$surveyid);
if (isset($scid)) //Would only come from email : we don't need it ....
{
$oCriteria->addCondition("{{saved_control}}.scid=:scid");
$aParams[':scid']=$scid;
}
$oCriteria->addCondition("{{saved_control}}.identifier=:identifier");
$aParams[':identifier']=$sLoadName;
if (in_array(Yii::app()->db->getDriverName(), array('mssql', 'sqlsrv', 'dblib')))
{
// To be validated with mssql, think it's not needed
$oCriteria->addCondition("(CAST({{saved_control}}.access_code as varchar(64))=:md5_code OR CAST({{saved_control}}.access_code as varchar(64))=:sha256_code)");
}
else
{
$oCriteria->addCondition("({{saved_control}}.access_code=:md5_code OR {{saved_control}}.access_code=:sha256_code)");
}
$aParams[':md5_code']=md5($sLoadPass);
$aParams[':sha256_code']=hash('sha256',$sLoadPass);
}
elseif (isset($_SESSION['survey_'.$surveyid]['srid']))
{
$oCriteria= new CDbCriteria;
$oCriteria->condition="id=:id";
$aParams=array(':id'=>$_SESSION['survey_'.$surveyid]['srid']);
}
else
{
return;
}
$oCriteria->params=$aParams;
$oResponses=SurveyDynamic::model($surveyid)->find($oCriteria);
if (!$oResponses)
{
return false;
}
else
{
//A match has been found. Let's load the values!
//If this is from an email, build surveysession first
$_SESSION['survey_'.$surveyid]['LEMtokenResume']=true;
// If survey come from reload (GET or POST); some value need to be found on saved_control, not on survey
if (Yii::app()->request->getParam('loadall') == "reload")
{
$oSavedSurvey=SavedControl::model()->find("identifier=:identifier AND (access_code=:access_code OR access_code=:sha256_code)",array(':identifier'=>$sLoadName,':access_code'=>md5($sLoadPass),':sha256_code'=>hash('sha256',$sLoadPass)));
// We don't need to control if we have one, because we do the test before
$_SESSION['survey_'.$surveyid]['scid'] = $oSavedSurvey->scid;
$_SESSION['survey_'.$surveyid]['step'] = ($oSavedSurvey->saved_thisstep>1)?$oSavedSurvey->saved_thisstep:1;
$thisstep=$_SESSION['survey_'.$surveyid]['step']-1;// deprecated ?
$_SESSION['survey_'.$surveyid]['srid'] = $oSavedSurvey->srid;// Seems OK without
$_SESSION['survey_'.$surveyid]['refurl'] = $oSavedSurvey->refurl;
}
// Get if survey is been answered
$submitdate=$oResponses->submitdate;
$aRow=$oResponses->attributes;
foreach ($aRow as $column => $value)
{
if ($column == "token")
{
$clienttoken=$value;
$token=$value;
}
elseif ($column =='lastpage' && !isset($_SESSION['survey_'.$surveyid]['step']))
{
if(is_null($submitdate) || $submitdate=="N")
{
$_SESSION['survey_'.$surveyid]['step']=($value>1? $value:1) ;
$thisstep=$_SESSION['survey_'.$surveyid]['step']-1;
}
else
{
$_SESSION['survey_'.$surveyid]['maxstep']=($value>1? $value:1) ;
}
}
elseif ($column == "datestamp")
{
$_SESSION['survey_'.$surveyid]['datestamp']=$value;
}
if ($column == "startdate")
{
$_SESSION['survey_'.$surveyid]['startdate']=$value;
}
else
{
//Only make session variables for those in insertarray[]
if (in_array($column, $_SESSION['survey_'.$surveyid]['insertarray']) && isset($_SESSION['survey_'.$surveyid]['fieldmap'][$column]))
{
if (($_SESSION['survey_'.$surveyid]['fieldmap'][$column]['type'] == 'N' ||
$_SESSION['survey_'.$surveyid]['fieldmap'][$column]['type'] == 'K' ||
$_SESSION['survey_'.$surveyid]['fieldmap'][$column]['type'] == 'D') && $value == null)
{ // For type N,K,D NULL in DB is to be considered as NoAnswer in any case.
// We need to set the _SESSION[field] value to '' in order to evaluate conditions.
// This is especially important for the deletenonvalue feature,
// otherwise we would erase any answer with condition such as EQUALS-NO-ANSWER on such
// question types (NKD)
$_SESSION['survey_'.$surveyid][$column]='';
}
else
{
$_SESSION['survey_'.$surveyid][$column]=$value;
}
} // if (in_array(
} // else
} // foreach
return true;
}
}
function makegraph($currentstep, $total)
{
global $thissurvey;
Yii::app()->getClientScript()->registerCssFile(Yii::app()->getConfig('publicstyleurl') . 'lime-progress.css');
$size = intval(($currentstep-1)/$total*100);
$graph = '<script type="text/javascript">
$(document).ready(function() {
$("#progressbar").progressbar({
value: '.$size.'
});
;});';
if (App()->getLocale()->orientation == 'rtl')
{
$graph.='
$(document).ready(function() {
$("div.ui-progressbar-value").removeClass("ui-corner-left");
$("div.ui-progressbar-value").addClass("ui-corner-right");
});';
}
$graph.='
</script>
<div id="progress-wrapper">
<span class="hide">'.sprintf(gT('You have completed %s%% of this survey'),$size).'</span>
<div id="progress-pre">';
if (App()->getLocale()->orientation == 'rtl')
{
$graph.='100%';
}
else
{
$graph.='0%';
}
$graph.='</div>
<div id="progressbar"></div>
<div id="progress-post">';
if (App()->getLocale()->orientation == 'rtl')
{
$graph.='0%';
}
else
{
$graph.='100%';
}
$graph.='</div>
</div>';
if ($size == 0) // Progress bar looks dumb if 0
{
$graph.='
<script type="text/javascript">
$(document).ready(function() {
$("div.ui-progressbar-value").hide();
});
</script>';
}
return $graph;
}
/**
* This function creates the language selector for a particular survey
*
* @param mixed $sSelectedLanguage The language in which all information is shown
*/
function makeLanguageChangerSurvey($sSelectedLanguage)
{
$surveyid = Yii::app()->getConfig('surveyID');
Yii::app()->loadHelper("surveytranslator");
$aSurveyLangs = Survey::model()->findByPk($surveyid)->getAllLanguages();
if (count($aSurveyLangs)>1) // return a dropdow only of there are more than one lanagage
{
$aAllLanguages=getLanguageData(true);
$aSurveyLangs=array_intersect_key($aAllLanguages,array_flip($aSurveyLangs)); // Sort languages by their locale name
$sClass="languagechanger";
$sHTMLCode="";
$sAction=Yii::app()->request->getParam('action','');// Different behaviour if preview
$sSelected="";
if(substr($sAction,0,7)=='preview')
{
$route="/survey/index/sid/{$surveyid}";
if ($sAction=='previewgroup' && intval(Yii::app()->request->getParam('gid',0)))
{
$route.="/action/previewgroup/gid/".intval(Yii::app()->request->getParam('gid',0));
}
if ($sAction=='previewquestion' && intval(Yii::app()->request->getParam('gid',0)) && intval(Yii::app()->request->getParam('qid',0)))
{
$route.="/action/previewquestion/gid/".intval(Yii::app()->request->getParam('gid',0))."/qid/".intval(Yii::app()->request->getParam('qid',0));
}
if (!is_null(Yii::app()->request->getParam('token')))
{
$route.="/token/".Yii::app()->request->getParam('token');
}
$sClass.=" previewmode";
// Maybe add other param (for prefilling by URL): then need a real createUrl with array
# foreach ($aSurveyLangs as $sLangCode => $aSurveyLang)
# {
# $sTargetURL=Yii::app()->getController()->createUrl($route."/lang/$sLangCode");
# $aListLang[$sTargetURL]=html_entity_decode($aSurveyLang['nativedescription'], ENT_COMPAT,'UTF-8');
# if(App()->language==$sLangCode)
# $sSelected=$sTargetURL;
# }
}
else
{
$route="/survey/index/sid/{$surveyid}";
}
$sTargetURL=Yii::app()->getController()->createUrl($route);
foreach ($aSurveyLangs as $sLangCode => $aSurveyLang)
{
$aListLang[$sLangCode]=html_entity_decode($aSurveyLang['nativedescription'], ENT_COMPAT,'UTF-8');
}
$sSelected=App()->language;
$sHTMLCode=CHtml::label(gT("Choose another language"), 'lang',array('class'=>'hide label'));
$sHTMLCode.=CHtml::dropDownList('lang', $sSelected,$aListLang,array('class'=>$sClass,'data-targeturl'=>$sTargetURL));
// We don't have to add this button if in previewmode
$sHTMLCode.= CHtml::htmlButton(gT("Change the language"),array('type'=>'submit','id'=>"changelangbtn",'value'=>'changelang','name'=>'changelang','class'=>'changelang jshide'));
return $sHTMLCode;
}
else
{
return false;
}
}
/**
* This function creates the language selector for the public survey index page
*
* @param mixed $sSelectedLanguage The language in which all information is shown
*/
function makeLanguageChanger($sSelectedLanguage)
{
$aLanguages=getLanguageDataRestricted(true,$sSelectedLanguage);// Order by native
if(count($aLanguages)>1)
{
# $sHTMLCode = "<select id='languagechanger' name='languagechanger' class='languagechanger' onchange='javascript:window.location=this.value'>\n";
# foreach(getLanguageDataRestricted(true, $sSelectedLanguage) as $sLanguageID=>$aLanguageProperties)
# {
# $sLanguageUrl=Yii::app()->getController()->createUrl('survey/index',array('lang'=>$sLanguageID));
# $sHTMLCode .= "<option value='{$sLanguageUrl}'";
# if($sLanguageID == $sSelectedLanguage)
# {
# $sHTMLCode .= " selected='selected' ";
# $sHTMLCode .= ">{$aLanguageProperties['nativedescription']}</option>\n";
# }
# else
# {
# $sHTMLCode .= ">".$aLanguageProperties['nativedescription'].' - '.$aLanguageProperties['description']."</option>\n";
# }
# }
# $sHTMLCode .= "</select>\n";
$sClass= "languagechanger";
foreach ($aLanguages as $sLangCode => $aLanguage)
$aListLang[$sLangCode]=html_entity_decode($aLanguage['nativedescription'], ENT_COMPAT,'UTF-8').' - '.$aLanguage['description'];
$sSelected=$sSelectedLanguage;
$sHTMLCode= CHtml::beginForm(App()->createUrl('surveys/publiclist'),'get');
$sHTMLCode.=CHtml::label(gT("Choose another language"), 'lang',array('class'=>'hide label'));
$sHTMLCode.= CHtml::dropDownList('lang', $sSelected,$aListLang,array('class'=>$sClass));
//$sHTMLCode.= CHtml::htmlButton(gT("Change the language"),array('type'=>'submit','id'=>"changelangbtn",'value'=>'changelang','name'=>'changelang','class'=>'jshide'));
$sHTMLCode.="<button class='changelang jshide' value='changelang' id='changelangbtn' type='submit'>".gT("Change the language")."</button>";
$sHTMLCode.= CHtml::endForm();
return $sHTMLCode;
}
else
{
return false;
}
}
/**
* checkUploadedFileValidity used in SurveyRuntimeHelper
*/
function checkUploadedFileValidity($surveyid, $move, $backok=null)
{
global $thisstep;
if (!isset($backok) || $backok != "Y")
{
$fieldmap = createFieldMap($surveyid,'full',false,false,$_SESSION['survey_'.$surveyid]['s_lang']);
if (isset($_POST['fieldnames']) && $_POST['fieldnames']!="")
{
$fields = explode("|", $_POST['fieldnames']);
foreach ($fields as $field)
{
if ($fieldmap[$field]['type'] == "|" && !strrpos($fieldmap[$field]['fieldname'], "_filecount"))
{
$validation= getQuestionAttributeValues($fieldmap[$field]['qid']);
$filecount = 0;
$json = $_POST[$field];
// if name is blank, its basic, hence check
// else, its ajax, don't check, bypass it.
if ($json != "" && $json != "[]")
{
$phparray = json_decode(stripslashes($json));
if ($phparray[0]->size != "")
{ // ajax
$filecount = count($phparray);
}
else
{ // basic
for ($i = 1; $i <= $validation['max_num_of_files']; $i++)
{
if (!isset($_FILES[$field."_file_".$i]) || $_FILES[$field."_file_".$i]['name'] == '')
continue;
$filecount++;
$file = $_FILES[$field."_file_".$i];
// File size validation
if ($file['size'] > $validation['max_filesize'] * 1000)
{
$filenotvalidated = array();
$filenotvalidated[$field."_file_".$i] = sprintf(gT("Sorry, the uploaded file (%s) is larger than the allowed filesize of %s KB."), $file['size'], $validation['max_filesize']);
$append = true;
}
// File extension validation
$pathinfo = pathinfo(basename($file['name']));
$ext = $pathinfo['extension'];
$validExtensions = explode(",", $validation['allowed_filetypes']);
if (!(in_array($ext, $validExtensions)))
{
if (isset($append) && $append)
{
$filenotvalidated[$field."_file_".$i] .= sprintf(gT("Sorry, only %s extensions are allowed!"),$validation['allowed_filetypes']);
unset($append);
}
else
{
$filenotvalidated = array();
$filenotvalidated[$field."_file_".$i] .= sprintf(gT("Sorry, only %s extensions are allowed!"),$validation['allowed_filetypes']);
}
}
}
}
}
else
$filecount = 0;
if (isset($validation['min_num_of_files']) && $filecount < $validation['min_num_of_files'] && LimeExpressionManager::QuestionIsRelevant($fieldmap[$field]['qid']))
{
$filenotvalidated = array();
$filenotvalidated[$field] = gT("The minimum number of files has not been uploaded.");
}
}
}
}
if (isset($filenotvalidated))
{
if (isset($move) && $move == "moveprev")
$_SESSION['survey_'.$surveyid]['step'] = $thisstep;
if (isset($move) && $move == "movenext")
$_SESSION['survey_'.$surveyid]['step'] = $thisstep;
return $filenotvalidated;
}
}
if (!isset($filenotvalidated))
return false;
else
return $filenotvalidated;
}
/**
* Takes two single element arrays and adds second to end of first if value exists
* Why not use array_merge($array1,array_filter($array2);
*/
function addtoarray_single($array1, $array2)
{
//
if (is_array($array2))
{
foreach ($array2 as $ar)
{
if ($ar && $ar !== null)
{
$array1[]=$ar;
}
}
}
return $array1;
}
/**
* Marks a tokens as completed and sends a confirmation email to the participiant.
* If $quotaexit is set to true then the user exited the survey due to a quota
* restriction and the according token is only marked as 'Q'
*
* @param mixed $quotaexit
*/
function submittokens($quotaexit=false)
{
$surveyid=Yii::app()->getConfig('surveyID');
if(isset($_SESSION['survey_'.$surveyid]['s_lang']))
{
$thissurvey=getSurveyInfo($surveyid,$_SESSION['survey_'.$surveyid]['s_lang']);
}
else
{
$thissurvey=getSurveyInfo($surveyid);
}
$clienttoken = $_SESSION['survey_'.$surveyid]['token'];
$sitename = Yii::app()->getConfig("sitename");
$emailcharset = Yii::app()->getConfig("emailcharset");
// Shift the date due to global timeadjust setting
$today = dateShift(date("Y-m-d H:i:s"), "Y-m-d H:i", Yii::app()->getConfig("timeadjust"));
// check how many uses the token has left
$token = Token::model($surveyid)->findByAttributes(array('token' => $clienttoken));
if ($quotaexit==true)
{
$token->completed = 'Q';
$token->usesleft--;
}
else
{
if ($token->usesleft <= 1)
{
// Finish the token
if (isTokenCompletedDatestamped($thissurvey))
{
$token->completed = $today;
} else {
$token->completed = 'Y';
}
if(isset($token->participant_id))
{
$slquery = SurveyLink::model()->find('participant_id = :pid AND survey_id = :sid AND token_id = :tid', array(':pid'=> $token->participant_id, ':sid'=>$surveyid, ':tid'=>$token->tid));
if ($slquery)
{
if (isTokenCompletedDatestamped($thissurvey))
{
$slquery->date_completed = $today;
} else {
// Update the survey_links table if necessary, to protect anonymity, use the date_created field date
$slquery->date_completed = $slquery->date_created;
}
$slquery->save();
}
}
}
$token->usesleft--;
}
$token->save();
if ($quotaexit==false)
{
if ($token && trim(strip_tags($thissurvey['email_confirm'])) != "" && $thissurvey['sendconfirmation'] == "Y")
{
// if($token->completed == "Y" || $token->completed == $today)
// {
$from = "{$thissurvey['adminname']} <{$thissurvey['adminemail']}>";
$subject=$thissurvey['email_confirm_subj'];
$aReplacementVars=array();
$aReplacementVars["ADMINNAME"]=$thissurvey['admin'];
$aReplacementVars["ADMINEMAIL"]=$thissurvey['adminemail'];
$aReplacementVars['ADMINEMAIL'] = $thissurvey['adminemail'];
//Fill with token info, because user can have his information with anonimity control
$aReplacementVars["FIRSTNAME"]=$token->firstname;
$aReplacementVars["LASTNAME"]=$token->lastname;
$aReplacementVars["TOKEN"]=$token->token;
// added survey url in replacement vars
$surveylink = Yii::app()->createAbsoluteUrl("/survey/index/sid/{$surveyid}",array('lang'=>$_SESSION['survey_'.$surveyid]['s_lang'],'token'=>$token->token));
$aReplacementVars['SURVEYURL'] = $surveylink;
$attrfieldnames=getAttributeFieldNames($surveyid);
foreach ($attrfieldnames as $attr_name)
{
$aReplacementVars[strtoupper($attr_name)] = $token->$attr_name;
}
$dateformatdatat=getDateFormatData($thissurvey['surveyls_dateformat']);
$numberformatdatat = getRadixPointData($thissurvey['surveyls_numberformat']);
$redata=array('thissurvey'=>$thissurvey);
$subject=templatereplace($subject,$aReplacementVars,$redata,'email_confirm_subj', false, NULL, array(), true );
$subject=html_entity_decode($subject,ENT_QUOTES,$emailcharset);
if (getEmailFormat($surveyid) == 'html')
{
$ishtml=true;
}
else
{
$ishtml=false;
}
$message=$thissurvey['email_confirm'];
//$message=ReplaceFields($message, $fieldsarray, true);
$message=templatereplace($message,$aReplacementVars,$redata,'email_confirm', false, NULL, array(), true );
if (!$ishtml)
{
$message=strip_tags(breakToNewline(html_entity_decode($message,ENT_QUOTES,$emailcharset)));
}
else
{
$message=html_entity_decode($message,ENT_QUOTES, $emailcharset );
}
//Only send confirmation email if there is a valid email address
$sToAddress=validateEmailAddresses($token->email);
if ($sToAddress) {
$aAttachments = unserialize($thissurvey['attachments']);
$aRelevantAttachments = array();
/*
* Iterate through attachments and check them for relevance.
*/
if (isset($aAttachments['confirmation']))
{
foreach ($aAttachments['confirmation'] as $aAttachment)
{
$relevance = $aAttachment['relevance'];
// If the attachment is relevant it will be added to the mail.
if (LimeExpressionManager::ProcessRelevance($relevance) && file_exists($aAttachment['url']))
{
$aRelevantAttachments[] = $aAttachment['url'];
}
}
}
SendEmailMessage($message, $subject, $sToAddress, $from, $sitename, $ishtml, null, $aRelevantAttachments);
}
// } else {
// Leave it to send optional confirmation at closed token
// }
}
}
}
/**
* Send a submit notification to the email address specified in the notifications tab in the survey settings
*/
function sendSubmitNotifications($surveyid)
{
// @todo: Remove globals
global $thissurvey, $maildebug, $tokensexist;
if (trim($thissurvey['adminemail'])=='')
{
return;
}
$homeurl=Yii::app()->createAbsoluteUrl('/admin');
$sitename = Yii::app()->getConfig("sitename");
$debug=Yii::app()->getConfig('debug');
$bIsHTML = ($thissurvey['htmlemail'] == 'Y');
$aReplacementVars=array();
if ($thissurvey['allowsave'] == "Y" && isset($_SESSION['survey_'.$surveyid]['scid']))
{
$aReplacementVars['RELOADURL']="".Yii::app()->getController()->createUrl("/survey/index/sid/{$surveyid}/loadall/reload/scid/".$_SESSION['survey_'.$surveyid]['scid']."/loadname/".urlencode($_SESSION['survey_'.$surveyid]['holdname'])."/loadpass/".urlencode($_SESSION['survey_'.$surveyid]['holdpass'])."/lang/".urlencode(App()->language));
if ($bIsHTML)
{
$aReplacementVars['RELOADURL']="<a href='{$aReplacementVars['RELOADURL']}'>{$aReplacementVars['RELOADURL']}</a>";
}
}
else
{
$aReplacementVars['RELOADURL']='';
}
if (!isset($_SESSION['survey_'.$surveyid]['srid']))
$srid = null;
else
$srid = $_SESSION['survey_'.$surveyid]['srid'];
$aReplacementVars['ADMINNAME'] = $thissurvey['adminname'];
$aReplacementVars['ADMINEMAIL'] = $thissurvey['adminemail'];
$aReplacementVars['VIEWRESPONSEURL']=Yii::app()->createAbsoluteUrl("/admin/responses/sa/view/surveyid/{$surveyid}/id/{$srid}");
$aReplacementVars['EDITRESPONSEURL']=Yii::app()->createAbsoluteUrl("/admin/dataentry/sa/editdata/subaction/edit/surveyid/{$surveyid}/id/{$srid}");
$aReplacementVars['STATISTICSURL']=Yii::app()->createAbsoluteUrl("/admin/statistics/sa/index/surveyid/{$surveyid}");
if ($bIsHTML)
{
$aReplacementVars['VIEWRESPONSEURL']="<a href='{$aReplacementVars['VIEWRESPONSEURL']}'>{$aReplacementVars['VIEWRESPONSEURL']}</a>";
$aReplacementVars['EDITRESPONSEURL']="<a href='{$aReplacementVars['EDITRESPONSEURL']}'>{$aReplacementVars['EDITRESPONSEURL']}</a>";
$aReplacementVars['STATISTICSURL']="<a href='{$aReplacementVars['STATISTICSURL']}'>{$aReplacementVars['STATISTICSURL']}</a>";
}
$aReplacementVars['ANSWERTABLE']='';
$aEmailResponseTo=array();
$aEmailNotificationTo=array();
$sResponseData="";
if (!empty($thissurvey['emailnotificationto']))
{
$aRecipient=explode(";", ReplaceFields($thissurvey['emailnotificationto'],array('ADMINEMAIL' =>$thissurvey['adminemail'] ), true));
foreach($aRecipient as $sRecipient)
{
$sRecipient=trim($sRecipient);
if(validateEmailAddress($sRecipient))
{
$aEmailNotificationTo[]=$sRecipient;
}
}
}
if (!empty($thissurvey['emailresponseto']))
{
// there was no token used so lets remove the token field from insertarray
if (!isset($_SESSION['survey_'.$surveyid]['token']) && $_SESSION['survey_'.$surveyid]['insertarray'][0]=='token')
{
unset($_SESSION['survey_'.$surveyid]['insertarray'][0]);
}
//Make an array of email addresses to send to
$aRecipient=explode(";", ReplaceFields($thissurvey['emailresponseto'],array('ADMINEMAIL' =>$thissurvey['adminemail'] ), true));
foreach($aRecipient as $sRecipient)
{
$sRecipient=trim($sRecipient);
if(validateEmailAddress($sRecipient))
{
$aEmailResponseTo[]=$sRecipient;
}
}
$aFullResponseTable=getFullResponseTable($surveyid,$_SESSION['survey_'.$surveyid]['srid'],$_SESSION['survey_'.$surveyid]['s_lang']);
$ResultTableHTML = "<table class='printouttable' >\n";
$ResultTableText ="\n\n";
$oldgid = 0;
$oldqid = 0;
foreach ($aFullResponseTable as $sFieldname=>$fname)
{
if (substr($sFieldname,0,4)=='gid_')
{
$ResultTableHTML .= "\t<tr class='printanswersgroup'><td colspan='2'>".strip_tags($fname[0])."</td></tr>\n";
$ResultTableText .="\n{$fname[0]}\n\n";
}
elseif (substr($sFieldname,0,4)=='qid_')
{
$ResultTableHTML .= "\t<tr class='printanswersquestionhead'><td colspan='2'>".strip_tags($fname[0])."</td></tr>\n";
$ResultTableText .="\n{$fname[0]}\n";
}
else
{
$ResultTableHTML .= "\t<tr class='printanswersquestion'><td>".strip_tags("{$fname[0]} {$fname[1]}")."</td><td class='printanswersanswertext'>".CHtml::encode($fname[2])."</td></tr>\n";
$ResultTableText .=" {$fname[0]} {$fname[1]}: {$fname[2]}\n";
}
}
$ResultTableHTML .= "</table>\n";
$ResultTableText .= "\n\n";
if ($bIsHTML)
{
$aReplacementVars['ANSWERTABLE']=$ResultTableHTML;
}
else
{
$aReplacementVars['ANSWERTABLE']=$ResultTableText;
}
}
$sFrom = $thissurvey['adminname'].' <'.$thissurvey['adminemail'].'>';
$aAttachments = unserialize($thissurvey['attachments']);
$aRelevantAttachments = array();
/*
* Iterate through attachments and check them for relevance.
*/
if (isset($aAttachments['admin_notification']))
{
foreach ($aAttachments['admin_notification'] as $aAttachment)
{
$relevance = $aAttachment['relevance'];
// If the attachment is relevant it will be added to the mail.
if (LimeExpressionManager::ProcessRelevance($relevance) && file_exists($aAttachment['url']))
{
$aRelevantAttachments[] = $aAttachment['url'];
}
}
}
$redata=compact(array_keys(get_defined_vars()));
if (count($aEmailNotificationTo)>0)
{
$sMessage=templatereplace($thissurvey['email_admin_notification'],$aReplacementVars,$redata,'admin_notification',$thissurvey['anonymized'] == "Y",NULL, array(), true);
$sSubject=templatereplace($thissurvey['email_admin_notification_subj'],$aReplacementVars,$redata,'admin_notification_subj',($thissurvey['anonymized'] == "Y"),NULL, array(), true);
foreach ($aEmailNotificationTo as $sRecipient)
{
if (!SendEmailMessage($sMessage, $sSubject, $sRecipient, $sFrom, $sitename, true, getBounceEmail($surveyid), $aRelevantAttachments))
{
if ($debug>0)
{
echo '<br />Email could not be sent. Reason: '.$maildebug.'<br/>';
}
}
}
}
$aRelevantAttachments = array();
/*
* Iterate through attachments and check them for relevance.
*/
if (isset($aAttachments['detailed_admin_notification']))
{
foreach ($aAttachments['detailed_admin_notification'] as $aAttachment)
{
$relevance = $aAttachment['relevance'];
// If the attachment is relevant it will be added to the mail.
if (LimeExpressionManager::ProcessRelevance($relevance) && file_exists($aAttachment['url']))
{
$aRelevantAttachments[] = $aAttachment['url'];
}
}
}
if (count($aEmailResponseTo)>0)
{
$sMessage=templatereplace($thissurvey['email_admin_responses'],$aReplacementVars,$redata,'detailed_admin_notification',$thissurvey['anonymized'] == "Y",NULL, array(), true);
$sSubject=templatereplace($thissurvey['email_admin_responses_subj'],$aReplacementVars,$redata,'detailed_admin_notification_subj',$thissurvey['anonymized'] == "Y",NULL, array(), true);
foreach ($aEmailResponseTo as $sRecipient)
{
if (!SendEmailMessage($sMessage, $sSubject, $sRecipient, $sFrom, $sitename, true, getBounceEmail($surveyid), $aRelevantAttachments))
{
if ($debug>0)
{
echo '<br />Email could not be sent. Reason: '.$maildebug.'<br/>';
}
}
}
}
}
/**
* submitfailed : used in em_manager_helper.php
*/
function submitfailed($errormsg='')
{
global $debug;
global $thissurvey;
global $subquery, $surveyid;
$completed = "<br /><strong><font size='2' color='red'>"
. gT("Did Not Save")."</strong></font><br /><br />\n\n"
. gT("An unexpected error has occurred and your responses cannot be saved.")."<br /><br />\n";
if ($thissurvey['adminemail'])
{
$completed .= gT("Your responses have not been lost and have been emailed to the survey administrator and will be entered into our database at a later point.")."<br /><br />\n";
if ($debug>0)
{
$completed.='Error message: '.htmlspecialchars($errormsg).'<br />';
}
$email=gT("An error occurred saving a response to survey id","unescaped")." ".$thissurvey['name']." - $surveyid\n\n";
$email .= gT("DATA TO BE ENTERED","unescaped").":\n";
foreach ($_SESSION['survey_'.$surveyid]['insertarray'] as $value)
{
$email .= "$value: {$_SESSION['survey_'.$surveyid][$value]}\n";
}
$email .= "\n".gT("SQL CODE THAT FAILED","unescaped").":\n"
. "$subquery\n\n"
. gT("ERROR MESSAGE","unescaped").":\n"
. $errormsg."\n\n";
SendEmailMessage($email, gT("Error saving results","unescaped"), $thissurvey['adminemail'], $thissurvey['adminemail'], "LimeSurvey", false, getBounceEmail($surveyid));
//echo "<!-- EMAIL CONTENTS:\n$email -->\n";
//An email has been sent, so we can kill off this session.
killSurveySession($surveyid);
}
else
{
$completed .= "<a href='javascript:location.reload()'>".gT("Try to submit again")."</a><br /><br />\n";
$completed .= $subquery;
}
return $completed;
}
/**
* This function builds all the required session variables when a survey is first started and
* it loads any answer defaults from command line or from the table defaultvalues
* It is called from the related format script (group.php, question.php, survey.php)
* if the survey has just started.
*/
function buildsurveysession($surveyid,$preview=false)
{
Yii::trace('start', 'survey.buildsurveysession');
global $secerror, $clienttoken;
global $tokensexist;
//global $surveyid;
global $move, $rooturl;
$sLangCode=App()->language;
$languagechanger=makeLanguageChangerSurvey($sLangCode);
if(!$preview)
$preview=Yii::app()->getConfig('previewmode');
$thissurvey = getSurveyInfo($surveyid,$sLangCode);
$_SESSION['survey_'.$surveyid]['templatename']=$thissurvey['template'];// $thissurvey['template'] already fixed by model : but why put this in session ?
$_SESSION['survey_'.$surveyid]['templatepath']=getTemplatePath($thissurvey['template']).DIRECTORY_SEPARATOR;
$sTemplatePath=$_SESSION['survey_'.$surveyid]['templatepath'];
$loadsecurity = returnGlobal('loadsecurity',true);
// NO TOKEN REQUIRED BUT CAPTCHA ENABLED FOR SURVEY ACCESS
if ($tokensexist == 0 && isCaptchaEnabled('surveyaccessscreen',$thissurvey['usecaptcha']) && !isset($_SESSION['survey_'.$surveyid]['captcha_surveyaccessscreen'])&& !$preview)
{
// IF CAPTCHA ANSWER IS NOT CORRECT OR NOT SET
if (!isset($loadsecurity) ||
!isset($_SESSION['survey_'.$surveyid]['secanswer']) ||
$loadsecurity != $_SESSION['survey_'.$surveyid]['secanswer'])
{
sendCacheHeaders();
doHeader();
// No or bad answer to required security question
$redata = compact(array_keys(get_defined_vars()));
echo templatereplace(file_get_contents($sTemplatePath."startpage.pstpl"),array(),$redata,'frontend_helper[875]');
//echo makedropdownlist();
echo templatereplace(file_get_contents($sTemplatePath."survey.pstpl"),array(),$redata,'frontend_helper[877]');
if (isset($loadsecurity))
{ // was a bad answer
echo "<font color='#FF0000'>".gT("The answer to the security question is incorrect.")."</font><br />";
}
echo "<p class='captcha'>".gT("Please confirm access to survey by answering the security question below and click continue.")."</p>"
.CHtml::form(array("/survey/index","sid"=>$surveyid), 'post', array('class'=>'captcha'))."
<table align='center'>
<tr>
<td align='right' valign='middle'>
<input type='hidden' name='sid' value='".$surveyid."' id='sid' />
<input type='hidden' name='lang' value='".$sLangCode."' id='lang' />";
// In case we this is a direct Reload previous answers URL, then add hidden fields
if (isset($_GET['loadall']) && isset($_GET['scid'])
&& isset($_GET['loadname']) && isset($_GET['loadpass']))
{
echo "
<input type='hidden' name='loadall' value='".htmlspecialchars($_GET['loadall'],ENT_QUOTES, 'UTF-8')."' id='loadall' />
<input type='hidden' name='scid' value='".returnGlobal('scid',true)."' id='scid' />
<input type='hidden' name='loadname' value='".htmlspecialchars($_GET['loadname'],ENT_QUOTES, 'UTF-8')."' id='loadname' />
<input type='hidden' name='loadpass' value='".htmlspecialchars($_GET['loadpass'],ENT_QUOTES, 'UTF-8')."' id='loadpass' />";
}
echo "
</td>
</tr>";
if (function_exists("ImageCreate") && isCaptchaEnabled('surveyaccessscreen', $thissurvey['usecaptcha']))
{
echo "<tr>
<td align='center' valign='middle'><label for='captcha'>".gT("Security question:")."</label></td><td align='left' valign='middle'><table><tr><td valign='middle'><img src='".Yii::app()->getController()->createUrl('/verification/image/sid/'.$surveyid)."' alt='captcha' /></td>
<td valign='middle'><input id='captcha' type='text' size='5' maxlength='3' name='loadsecurity' value='' /></td></tr></table>
</td>
</tr>";
}
echo "<tr><td colspan='2' align='center'><input class='submit' type='submit' value='".gT("Continue")."' /></td></tr>
</table>
</form>";
echo templatereplace(file_get_contents($sTemplatePath."endpage.pstpl"),array(),$redata,'frontend_helper[1567]');
doFooter();
exit;
}
else{
$_SESSION['survey_'.$surveyid]['captcha_surveyaccessscreen']=true;
}
}
//BEFORE BUILDING A NEW SESSION FOR THIS SURVEY, LET'S CHECK TO MAKE SURE THE SURVEY SHOULD PROCEED!
// TOKEN REQUIRED BUT NO TOKEN PROVIDED
if ($tokensexist == 1 && !$clienttoken && !$preview)
{
if ($thissurvey['nokeyboard']=='Y')
{
includeKeypad();
$kpclass = "text-keypad";
}
else
{
$kpclass = "";
}
// DISPLAY REGISTER-PAGE if needed
// DISPLAY CAPTCHA if needed
if (isset($thissurvey) && $thissurvey['allowregister'] == "Y")
{
// Add the event and test if done
Yii::app()->runController("register/index/sid/{$surveyid}");
Yii::app()->end();
}
else
{
sendCacheHeaders();
doHeader();
$redata = compact(array_keys(get_defined_vars()));
echo templatereplace(file_get_contents($sTemplatePath."startpage.pstpl"),array(),$redata,'frontend_helper[1594]');
//echo makedropdownlist();
echo templatereplace(file_get_contents($sTemplatePath."survey.pstpl"),array(),$redata,'frontend_helper[1596]');
// ->renderPartial('entertoken_view');
if (isset($secerror)) echo "<span class='error'>".$secerror."</span><br />";
echo '<div id="wrapper"><p id="tokenmessage">'.gT("This is a controlled survey. You need a valid token to participate.")."<br />";
echo gT("If you have been issued a token, please enter it in the box below and click continue.")."</p>
<script type='text/javascript'>var focus_element='#token';</script>"
.CHtml::form(array("/survey/index","sid"=>$surveyid), 'post', array('id'=>'tokenform','autocomplete'=>'off'))."
<ul>
<li>";?>
<label for='token'><?php eT("Token:");?></label><input class='text <?php echo $kpclass?>' id='token' type='password' name='token' value='' />
<?php
echo "<input type='hidden' name='sid' value='".$surveyid."' id='sid' />
<input type='hidden' name='lang' value='".$sLangCode."' id='lang' />";
if (isset($_GET['newtest']) && $_GET['newtest'] == "Y")
{
echo " <input type='hidden' name='newtest' value='Y' id='newtest' />";
}
// If this is a direct Reload previous answers URL, then add hidden fields
if (isset($_GET['loadall']) && isset($_GET['scid'])
&& isset($_GET['loadname']) && isset($_GET['loadpass']))
{
echo "
<input type='hidden' name='loadall' value='".htmlspecialchars($_GET['loadall'],ENT_QUOTES, 'UTF-8')."' id='loadall' />
<input type='hidden' name='scid' value='".returnGlobal('scid',true)."' id='scid' />
<input type='hidden' name='loadname' value='".htmlspecialchars($_GET['loadname'],ENT_QUOTES, 'UTF-8')."' id='loadname' />
<input type='hidden' name='loadpass' value='".htmlspecialchars($_GET['loadpass'],ENT_QUOTES, 'UTF-8')."' id='loadpass' />";
}
echo "</li>";
if (function_exists("ImageCreate") && isCaptchaEnabled('surveyaccessscreen', $thissurvey['usecaptcha']))
{
echo "<li>
<label for='captchaimage'>".gT("Security Question")."</label><img id='captchaimage' src='".Yii::app()->getController()->createUrl('/verification/image/sid/'.$surveyid)."' alt='captcha' /><input type='text' size='5' maxlength='3' name='loadsecurity' value='' />
</li>";
}
echo "<li>
<input class='submit button' type='submit' value='".gT("Continue")."' />
</li>
</ul>
</form></div>";
echo templatereplace(file_get_contents($sTemplatePath."endpage.pstpl"),array(),$redata,'frontend_helper[1645]');
doFooter();
exit;
}
}
// TOKENS REQUIRED, A TOKEN PROVIDED
// SURVEY WITH NO NEED TO USE CAPTCHA
elseif ($tokensexist == 1 && $clienttoken &&
!isCaptchaEnabled('surveyaccessscreen',$thissurvey['usecaptcha']))
{
//check if token actually does exist
// check also if it is allowed to change survey after completion
if ($thissurvey['alloweditaftercompletion'] == 'Y' ) {
$oTokenEntry = Token::model($surveyid)->findByAttributes(array('token'=>$clienttoken));
} else {
$oTokenEntry = Token::model($surveyid)->usable()->incomplete()->findByAttributes(array('token' => $clienttoken));
}
if (!isset($oTokenEntry))
{
//TOKEN DOESN'T EXIST OR HAS ALREADY BEEN USED. EXPLAIN PROBLEM AND EXIT
killSurveySession($surveyid);
sendCacheHeaders();
doHeader();
$redata = compact(array_keys(get_defined_vars()));
echo templatereplace(file_get_contents($sTemplatePath."startpage.pstpl"),array(),$redata,'frontend_helper[1676]');
echo templatereplace(file_get_contents($sTemplatePath."survey.pstpl"),array(),$redata,'frontend_helper[1677]');
echo '<div id="wrapper"><p id="tokenmessage">'.gT("This is a controlled survey. You need a valid token to participate.")."<br /><br />\n"
."\t".gT("The token you have provided is either not valid, or has already been used.")."<br /><br />\n"
."\t".sprintf(gT("For further information please contact %s"), $thissurvey['adminname'])
." (<a href='mailto:{$thissurvey['adminemail']}'>"
."{$thissurvey['adminemail']}</a>)</p></div>\n";
echo templatereplace(file_get_contents($sTemplatePath."endpage.pstpl"),array(),$redata,'frontend_helper[1684]');
doFooter();
exit;
}
}
// TOKENS REQUIRED, A TOKEN PROVIDED
// SURVEY CAPTCHA REQUIRED
elseif ($tokensexist == 1 && $clienttoken && isCaptchaEnabled('surveyaccessscreen',$thissurvey['usecaptcha']))
{
// IF CAPTCHA ANSWER IS CORRECT
if (isset($loadsecurity) &&
isset($_SESSION['survey_'.$surveyid]['secanswer']) &&
$loadsecurity == $_SESSION['survey_'.$surveyid]['secanswer'])
{
if ($thissurvey['alloweditaftercompletion'] == 'Y' )
{
$oTokenEntry = Token::model($surveyid)->findByAttributes(array('token'=> $clienttoken));
}
else
{
$oTokenEntry = Token::model($surveyid)->incomplete()->findByAttributes(array(
'token' => $clienttoken
));
}
if (!isset($oTokenEntry))
{
sendCacheHeaders();
doHeader();
//TOKEN DOESN'T EXIST OR HAS ALREADY BEEN USED. EXPLAIN PROBLEM AND EXIT
$redata = compact(array_keys(get_defined_vars()));
echo templatereplace(file_get_contents($sTemplatePath."startpage.pstpl"),array(),$redata,'frontend_helper[1719]');
echo templatereplace(file_get_contents($sTemplatePath."survey.pstpl"),array(),$redata,'frontend_helper[1720]');
echo "\t<div id='wrapper'>\n"
."\t<p id='tokenmessage'>\n"
."\t".gT("This is a controlled survey. You need a valid token to participate.")."<br /><br />\n"
."\t".gT("The token you have provided is either not valid, or has already been used.")."<br/><br />\n"
."\t".sprintf(gT("For further information please contact %s"), $thissurvey['adminname'])
." (<a href='mailto:{$thissurvey['adminemail']}'>"
."{$thissurvey['adminemail']}</a>)\n"
."\t</p>\n"
."\t</div>\n";
echo templatereplace(file_get_contents($sTemplatePath."endpage.pstpl"),array(),$redata,'frontend_helper[1731]');
doFooter();
exit;
}
}
// IF CAPTCHA ANSWER IS NOT CORRECT
else if (!isset($move) || is_null($move))
{
unset($_SESSION['survey_'.$surveyid]['srid']);
$gettoken = $clienttoken;
sendCacheHeaders();
doHeader();
// No or bad answer to required security question
$redata = compact(array_keys(get_defined_vars()));
echo templatereplace(file_get_contents($sTemplatePath."startpage.pstpl"),array(),$redata,'frontend_helper[1745]');
echo templatereplace(file_get_contents($sTemplatePath."survey.pstpl"),array(),$redata,'frontend_helper[1746]');
// If token wasn't provided and public registration
// is enabled then show registration form
if ( !isset($gettoken) && isset($thissurvey) && $thissurvey['allowregister'] == "Y")
{
echo templatereplace(file_get_contents($sTemplatePath."register.pstpl"),array(),$redata,'frontend_helper[1751]');
}
else
{ // only show CAPTCHA
echo '<div id="wrapper"><p id="tokenmessage">';
if (isset($loadsecurity))
{ // was a bad answer
echo "<span class='error'>".gT("The answer to the security question is incorrect.")."</span><br />";
}
echo gT("This is a controlled survey. You need a valid token to participate.")."<br /><br />";
// IF TOKEN HAS BEEN GIVEN THEN AUTOFILL IT
// AND HIDE ENTRY FIELD
if (!isset($gettoken))
{
echo gT("If you have been issued a token, please enter it in the box below and click continue.")."</p>
<form id='tokenform' method='get' action='".Yii::app()->getController()->createUrl("/survey/index")."'>
<ul>
<li>
<input type='hidden' name='sid' value='".$surveyid."' id='sid' />
<input type='hidden' name='lang' value='".$sLangCode."' id='lang' />";
if (isset($_GET['loadall']) && isset($_GET['scid'])
&& isset($_GET['loadname']) && isset($_GET['loadpass']))
{
echo "<input type='hidden' name='loadall' value='".htmlspecialchars($_GET['loadall'],ENT_QUOTES, 'UTF-8')."' id='loadall' />
<input type='hidden' name='scid' value='".returnGlobal('scid',true)."' id='scid' />
<input type='hidden' name='loadname' value='".htmlspecialchars($_GET['loadname'],ENT_QUOTES, 'UTF-8')."' id='loadname' />
<input type='hidden' name='loadpass' value='".htmlspecialchars($_GET['loadpass'],ENT_QUOTES, 'UTF-8')."' id='loadpass' />";
}
echo '<label for="token">'.gT("Token")."</label><input class='text' type='password' id='token' name='token'></li>";
}
else
{
echo gT("Please confirm the token by answering the security question below and click continue.")."</p>
<form id='tokenform' method='get' action='".Yii::app()->getController()->createUrl("/survey/index")."'>
<ul>
<li>
<input type='hidden' name='sid' value='".$surveyid."' id='sid' />
<input type='hidden' name='lang' value='".$sLangCode."' id='lang' />";
if (isset($_GET['loadall']) && isset($_GET['scid'])
&& isset($_GET['loadname']) && isset($_GET['loadpass']))
{
echo "<input type='hidden' name='loadall' value='".htmlspecialchars($_GET['loadall'],ENT_QUOTES, 'UTF-8')."' id='loadall' />
<input type='hidden' name='scid' value='".returnGlobal('scid',true)."' id='scid' />
<input type='hidden' name='loadname' value='".htmlspecialchars($_GET['loadname'],ENT_QUOTES, 'UTF-8')."' id='loadname' />
<input type='hidden' name='loadpass' value='".htmlspecialchars($_GET['loadpass'],ENT_QUOTES, 'UTF-8')."' id='loadpass' />";
}
echo '<label for="token">'.gT("Token:")."</label><span id='token'>$gettoken</span>"
."<input type='hidden' name='token' value='$gettoken'></li>";
}
if (function_exists("ImageCreate") && isCaptchaEnabled('surveyaccessscreen', $thissurvey['usecaptcha']))
{
echo "<li>
<label for='captchaimage'>".gT("Security Question")."</label><img id='captchaimage' src='".Yii::app()->getController()->createUrl('/verification/image/sid/'.$surveyid)."' alt='captcha' /><input type='text' size='5' maxlength='3' name='loadsecurity' value='' />
</li>";
}
echo "<li><input class='submit' type='submit' value='".gT("Continue")."' /></li>
</ul>
</form>
</id>";
}
echo '</div>'.templatereplace(file_get_contents($sTemplatePath."endpage.pstpl"),array(),$redata,'frontend_helper[1817]');
doFooter();
exit;
}
}
//RESET ALL THE SESSION VARIABLES AND START AGAIN
unset($_SESSION['survey_'.$surveyid]['grouplist']);
unset($_SESSION['survey_'.$surveyid]['fieldarray']);
unset($_SESSION['survey_'.$surveyid]['insertarray']);
unset($_SESSION['survey_'.$surveyid]['fieldnamesInfo']);
unset($_SESSION['survey_'.$surveyid]['fieldmap-' . $surveyid . '-randMaster']);
unset($_SESSION['survey_'.$surveyid]['groupReMap']);
$_SESSION['survey_'.$surveyid]['fieldnamesInfo'] = Array();
// Multi lingual support order : by REQUEST, if not by Token->language else by survey default language
if (returnGlobal('lang',true))
{
$language_to_set=returnGlobal('lang',true);
}
elseif (isset($oTokenEntry) && $oTokenEntry)
{
// If survey have token : we have a $oTokenEntry
// Can use $oTokenEntry = Token::model($surveyid)->findByAttributes(array('token'=>$clienttoken)); if we move on another function : this par don't validate the token validity
$language_to_set=$oTokenEntry->language;
}
else
{
$language_to_set = $thissurvey['language'];
}
// Always SetSurveyLanguage : surveys controller SetSurveyLanguage too, if different : broke survey (#09769)
SetSurveyLanguage($surveyid, $language_to_set);
UpdateGroupList($surveyid, $_SESSION['survey_'.$surveyid]['s_lang']);
$sQuery = "SELECT count(*)\n"
." FROM {{groups}} INNER JOIN {{questions}} ON {{groups}}.gid = {{questions}}.gid\n"
." WHERE {{questions}}.sid=".$surveyid."\n"
." AND {{groups}}.language='".App()->getLanguage()."'\n"
." AND {{questions}}.language='".App()->getLanguage()."'\n"
." AND {{questions}}.parent_qid=0\n";
$totalquestions = Yii::app()->db->createCommand($sQuery)->queryScalar();
$sQuery= "select count(*) from {{groups}}
left join {{questions}} on {{groups}}.gid={{questions}}.gid
where {{groups}}.sid={$surveyid} and qid is null";
$iTotalGroupsWithoutQuestions = Yii::app()->db->createCommand($sQuery)->queryScalar();
// Fix totalquestions by substracting Test Display questions
$iNumberofQuestions=dbExecuteAssoc("SELECT count(*)\n"
." FROM {{questions}}"
." WHERE type in ('X','*')\n"
." AND sid={$surveyid}"
." AND language='".$_SESSION['survey_'.$surveyid]['s_lang']."'"
." AND parent_qid=0")->read();
$_SESSION['survey_'.$surveyid]['totalquestions'] = $totalquestions - (int) reset($iNumberofQuestions);
//2. SESSION VARIABLE: totalsteps
//The number of "pages" that will be presented in this survey
//The number of pages to be presented will differ depending on the survey format
switch($thissurvey['format'])
{
case "A":
$_SESSION['survey_'.$surveyid]['totalsteps']=1;
break;
case "G":
if (isset($_SESSION['survey_'.$surveyid]['grouplist']))
{
$_SESSION['survey_'.$surveyid]['totalsteps']=count($_SESSION['survey_'.$surveyid]['grouplist']);
}
break;
case "S":
$_SESSION['survey_'.$surveyid]['totalsteps']=$totalquestions;
}
if ($totalquestions == 0 || $iTotalGroupsWithoutQuestions>0) //break out and crash if there are no questions!
{
sendCacheHeaders();
doHeader();
$redata = compact(array_keys(get_defined_vars()));
echo templatereplace(file_get_contents($sTemplatePath."startpage.pstpl"),array(),$redata,'frontend_helper[1914]');
echo templatereplace(file_get_contents($sTemplatePath."survey.pstpl"),array(),$redata,'frontend_helper[1915]');
echo "\t<div id='wrapper'>\n"
."\t<p id='tokenmessage'>\n"
."\t".gT("This survey cannot be tested or completed for the following reason(s):")."<br />\n";
echo "<ul>";
if ($totalquestions == 0){
echo '<li>'.gT("There are no questions in this survey.").'</li>';
}
if ($iTotalGroupsWithoutQuestions == 0){
echo '<li>'.gT("There are empty question groups in this survey - please create at least one question within a question group.").'</li>';
}
echo "</ul>"
."\t".sprintf(gT("For further information please contact %s"), $thissurvey['adminname'])
." (<a href='mailto:{$thissurvey['adminemail']}'>"
."{$thissurvey['adminemail']}</a>)<br /><br />\n"
."\t</p>\n"
."\t</div>\n";
echo templatereplace(file_get_contents($sTemplatePath."endpage.pstpl"),array(),$redata,'frontend_helper[1925]');
doFooter();
exit;
}
//Perform a case insensitive natural sort on group name then question title of a multidimensional array
// usort($arows, 'groupOrderThenQuestionOrder');
//3. SESSION VARIABLE - insertarray
//An array containing information about used to insert the data into the db at the submit stage
//4. SESSION VARIABLE - fieldarray
//See rem at end..
if ($tokensexist == 1 && $clienttoken)
{
$_SESSION['survey_'.$surveyid]['token'] = $clienttoken;
}
if ($thissurvey['anonymized'] == "N")
{
$_SESSION['survey_'.$surveyid]['insertarray'][]= "token";
}
$qtypes=getQuestionTypeList('','array');
$fieldmap=createFieldMap($surveyid,'full',true,false,$_SESSION['survey_'.$surveyid]['s_lang']);
// Randomization groups for groups
$aRandomGroups=array();
$aGIDCompleteMap=array();
// first find all groups and their groups IDS
$criteria = new CDbCriteria;
$criteria->addColumnCondition(array('sid' => $surveyid, 'language' => $_SESSION['survey_'.$surveyid]['s_lang']));
$criteria->addCondition("randomization_group != ''");
$oData = QuestionGroup::model()->findAll($criteria);
foreach($oData as $aGroup)
{
$aRandomGroups[$aGroup['randomization_group']][] = $aGroup['gid'];
}
// Shuffle each group and create a map for old GID => new GID
foreach ($aRandomGroups as $sGroupName=>$aGIDs)
{
$aShuffledIDs=$aGIDs;
shuffle($aShuffledIDs);
$aGIDCompleteMap=$aGIDCompleteMap+array_combine($aGIDs,$aShuffledIDs);
}
$_SESSION['survey_' . $surveyid]['groupReMap'] = $aGIDCompleteMap;
$randomized = false; // So we can trigger reorder once for group and question randomization
// Now adjust the grouplist
if (count($aRandomGroups)>0 && !$preview)
{
$randomized = true; // So we can trigger reorder once for group and question randomization
// Now adjust the grouplist
Yii::import('application.helpers.frontend_helper', true); // make sure frontend helper is loaded
UpdateGroupList($surveyid, $_SESSION['survey_'.$surveyid]['s_lang']);
// ... and the fieldmap
// First create a fieldmap with GID as key
foreach ($fieldmap as $aField)
{
if (isset($aField['gid']))
{
$GroupFieldMap[$aField['gid']][]=$aField;
}
else{
$GroupFieldMap['other'][]=$aField;
}
}
// swap it
foreach ($GroupFieldMap as $iOldGid => $fields)
{
$iNewGid = $iOldGid;
if (isset($aGIDCompleteMap[$iOldGid]))
{
$iNewGid = $aGIDCompleteMap[$iOldGid];
}
$newGroupFieldMap[$iNewGid] = $GroupFieldMap[$iNewGid];
}
$GroupFieldMap = $newGroupFieldMap;
// and convert it back to a fieldmap
unset($fieldmap);
foreach($GroupFieldMap as $aGroupFields)
{
foreach ($aGroupFields as $aField)
{
if (isset($aField['fieldname'])) {
$fieldmap[$aField['fieldname']] = $aField; // isset() because of the shuffled flag above
}
}
}
unset($GroupFieldMap);
}
// Randomization groups for questions
// Find all defined randomization groups through question attribute values
$randomGroups=array();
if (in_array(Yii::app()->db->getDriverName(), array('mssql', 'sqlsrv', 'dblib')))
{
$rgquery = "SELECT attr.qid, CAST(value as varchar(255)) as value FROM {{question_attributes}} as attr right join {{questions}} as quests on attr.qid=quests.qid WHERE attribute='random_group' and CAST(value as varchar(255)) <> '' and sid=$surveyid GROUP BY attr.qid, CAST(value as varchar(255))";
}
else
{
$rgquery = "SELECT attr.qid, value FROM {{question_attributes}} as attr right join {{questions}} as quests on attr.qid=quests.qid WHERE attribute='random_group' and value <> '' and sid=$surveyid GROUP BY attr.qid, value";
}
$rgresult = dbExecuteAssoc($rgquery);
foreach($rgresult->readAll() as $rgrow)
{
// Get the question IDs for each randomization group
$randomGroups[$rgrow['value']][] = $rgrow['qid'];
}
// If we have randomization groups set, then lets cycle through each group and
// replace questions in the group with a randomly chosen one from the same group
if (count($randomGroups) > 0 && !$preview)
{
$randomized = true; // So we can trigger reorder once for group and question randomization
$copyFieldMap = array();
$oldQuestOrder = array();
$newQuestOrder = array();
$randGroupNames = array();
foreach ($randomGroups as $key=>$value)
{
$oldQuestOrder[$key] = $randomGroups[$key];
$newQuestOrder[$key] = $oldQuestOrder[$key];
// We shuffle the question list to get a random key->qid which will be used to swap from the old key
shuffle($newQuestOrder[$key]);
$randGroupNames[] = $key;
}
// Loop through the fieldmap and swap each question as they come up
foreach ($fieldmap as $fieldkey => $fieldval)
{
$found = 0;
foreach ($randomGroups as $gkey => $gval)
{
// We found a qid that is in the randomization group
if (isset($fieldval['qid']) && in_array($fieldval['qid'],$oldQuestOrder[$gkey]))
{
// Get the swapped question
$idx = array_search($fieldval['qid'],$oldQuestOrder[$gkey]);
foreach ($fieldmap as $key => $field)
{
if (isset($field['qid']) && $field['qid'] == $newQuestOrder[$gkey][$idx])
{
$field['random_gid'] = $fieldval['gid']; // It is possible to swap to another group
$copyFieldMap[$key] = $field;
}
}
$found = 1;
break;
} else
{
$found = 2;
}
}
if ($found == 2)
{
$copyFieldMap[$fieldkey]=$fieldval;
}
reset($randomGroups);
}
$fieldmap = $copyFieldMap;
}
if ($randomized === true)
{
// reset the sequencing counts
$gseq = -1;
$_gid = -1;
$qseq = -1;
$_qid = -1;
$copyFieldMap = array();
foreach ($fieldmap as $key => $val)
{
if ($val['gid'] != '')
{
if (isset($val['random_gid']))
{
$gid = $val['random_gid'];
} else {
$gid = $val['gid'];
}
if ($gid != $_gid)
{
$_gid = $gid;
++$gseq;
}
}
if ($val['qid'] != '' && $val['qid'] != $_qid)
{
$_qid = $val['qid'];
++$qseq;
}
if ($val['gid'] != '' && $val['qid'] != '')
{
$val['groupSeq'] = $gseq;
$val['questionSeq'] = $qseq;
}
$copyFieldMap[$key] = $val;
}
$fieldmap = $copyFieldMap;
unset($copyFieldMap);
$_SESSION['survey_'.$surveyid]['fieldmap-' . $surveyid . $_SESSION['survey_'.$surveyid]['s_lang']] = $fieldmap;
$_SESSION['survey_'.$surveyid]['fieldmap-' . $surveyid . '-randMaster'] = 'fieldmap-' . $surveyid . $_SESSION['survey_'.$surveyid]['s_lang'];
}
// TMSW Condition->Relevance: don't need hasconditions, or usedinconditions
$_SESSION['survey_'.$surveyid]['fieldmap']=$fieldmap;
foreach ($fieldmap as $field)
{
if (isset($field['qid']) && $field['qid']!='')
{
$_SESSION['survey_'.$surveyid]['fieldnamesInfo'][$field['fieldname']]=$field['sid'].'X'.$field['gid'].'X'.$field['qid'];
$_SESSION['survey_'.$surveyid]['insertarray'][]=$field['fieldname'];
//fieldarray ARRAY CONTENTS -
// [0]=questions.qid,
// [1]=fieldname,
// [2]=questions.title,
// [3]=questions.question
// [4]=questions.type,
// [5]=questions.gid,
// [6]=questions.mandatory,
// [7]=conditionsexist,
// [8]=usedinconditions
// [8]=usedinconditions
// [9]=used in group.php for question count
// [10]=new group id for question in randomization group (GroupbyGroup Mode)
if (!isset($_SESSION['survey_'.$surveyid]['fieldarray'][$field['sid'].'X'.$field['gid'].'X'.$field['qid']]))
{
//JUST IN CASE : PRECAUTION!
//following variables are set only if $style=="full" in createFieldMap() in common_helper.
//so, if $style = "short", set some default values here!
if (isset($field['title']))
$title = $field['title'];
else
$title = "";
if (isset($field['question']))
$question = $field['question'];
else
$question = "";
if (isset($field['mandatory']))
$mandatory = $field['mandatory'];
else
$mandatory = 'N';
if (isset($field['hasconditions']))
$hasconditions = $field['hasconditions'];
else
$hasconditions = 'N';
if (isset($field['usedinconditions']))
$usedinconditions = $field['usedinconditions'];
else
$usedinconditions = 'N';
$_SESSION['survey_'.$surveyid]['fieldarray'][$field['sid'].'X'.$field['gid'].'X'.$field['qid']]=array($field['qid'],
$field['sid'].'X'.$field['gid'].'X'.$field['qid'],
$title,
$question,
$field['type'],
$field['gid'],
$mandatory,
$hasconditions,
$usedinconditions);
}
if (isset($field['random_gid']))
{
$_SESSION['survey_'.$surveyid]['fieldarray'][$field['sid'].'X'.$field['gid'].'X'.$field['qid']][10] = $field['random_gid'];
}
}
}
// Prefill questions/answers from command line params
$reservedGetValues= array('token','sid','gid','qid','lang','newtest','action');
$startingValues=array();
if (isset($_GET))
{
foreach ($_GET as $k=>$v)
{
if (!in_array($k,$reservedGetValues) && isset($_SESSION['survey_'.$surveyid]['fieldmap'][$k]))
{
$startingValues[$k] = $v;
}
else
{ // Search question codes to use those for prefilling.
foreach($_SESSION['survey_'.$surveyid]['fieldmap'] as $sgqa => $details)
{
if ($details['title'] == $k)
{
$startingValues[$sgqa] = $v;
}
}
}
}
}
$_SESSION['survey_'.$surveyid]['startingValues']=$startingValues;
if (isset($_SESSION['survey_'.$surveyid]['fieldarray'])) $_SESSION['survey_'.$surveyid]['fieldarray']=array_values($_SESSION['survey_'.$surveyid]['fieldarray']);
//Check if a passthru label and value have been included in the query url
$oResult=SurveyURLParameter::model()->getParametersForSurvey($surveyid);
foreach($oResult->readAll() as $aRow)
{
if(isset($_GET[$aRow['parameter']]) && !$preview)
{
$_SESSION['survey_'.$surveyid]['urlparams'][$aRow['parameter']]=$_GET[$aRow['parameter']];
if ($aRow['targetqid']!='')
{
foreach ($fieldmap as $sFieldname=>$aField)
{
if ($aRow['targetsqid']!='')
{
if ($aField['qid']==$aRow['targetqid'] && $aField['sqid']==$aRow['targetsqid'])
{
$_SESSION['survey_'.$surveyid]['startingValues'][$sFieldname]=$_GET[$aRow['parameter']];
$_SESSION['survey_'.$surveyid]['startingValues'][$aRow['parameter']]=$_GET[$aRow['parameter']];
}
}
else
{
if ($aField['qid']==$aRow['targetqid'])
{
$_SESSION['survey_'.$surveyid]['startingValues'][$sFieldname]=$_GET[$aRow['parameter']];
$_SESSION['survey_'.$surveyid]['startingValues'][$aRow['parameter']]=$_GET[$aRow['parameter']];
}
}
}
}
}
}
Yii::trace('end', 'survey.buildsurveysession');
}
/**
* This function creates the form elements in the survey navigation bar
* Adding a hidden input for default behaviour without javascript
* Use button name="move" for real browser (with or without javascript) and IE6/7/8 with javascript
*/
function surveymover()
{
$surveyid=Yii::app()->getConfig('surveyID');
$thissurvey=getSurveyInfo($surveyid);
$sMoveNext="movenext";
$sMovePrev="";
$iSessionStep=(isset($_SESSION['survey_'.$surveyid]['step']))?$_SESSION['survey_'.$surveyid]['step']:false;
$iSessionMaxStep=(isset($_SESSION['survey_'.$surveyid]['maxstep']))?$_SESSION['survey_'.$surveyid]['maxstep']:false;
$iSessionTotalSteps=(isset($_SESSION['survey_'.$surveyid]['totalsteps']))?$_SESSION['survey_'.$surveyid]['totalsteps']:false;
$sClass="submit button";
$sSurveyMover = "";
// Count down
if ($thissurvey['navigationdelay'] > 0 && ($iSessionMaxStep!==false && $iSessionMaxStep == $iSessionStep))
{
$sClass.=" disabled";
App()->getClientScript()->registerScriptFile(Yii::app()->getConfig('generalscripts')."/navigator-countdown.js");
App()->getClientScript()->registerScript('navigator_countdown',"navigator_countdown(" . $thissurvey['navigationdelay'] . ");\n",CClientScript::POS_BEGIN);
}
// Previous ?
if ($thissurvey['format'] != "A" && ($thissurvey['allowprev'] != "N")
&& $iSessionStep
&& !($iSessionStep == 1 && $thissurvey['showwelcome'] == 'N')
&& !Yii::app()->getConfig('previewmode')
)
{
$sMovePrev="moveprev";
}
// Submit ?
if ($iSessionStep && ($iSessionStep == $iSessionTotalSteps)
|| $thissurvey['format'] == 'A'
)
{
$sMoveNext="movesubmit";
}
// todo Remove Next if needed (exemple quota show previous only: maybe other, but actually don't use surveymover)
if(Yii::app()->getConfig('previewmode'))
{
$sMoveNext="";
}
// Construction of mover
if($sMovePrev){
$sLangMoveprev=gT("Previous");
$sSurveyMover.= CHtml::htmlButton($sLangMoveprev,array('type'=>'submit','id'=>"{$sMovePrev}btn",'value'=>$sMovePrev,'name'=>$sMovePrev,'accesskey'=>'p','class'=>$sClass));
}
if($sMovePrev && $sMoveNext){
$sSurveyMover .= " ";
}
if($sMoveNext){
if($sMoveNext=="movesubmit"){
$sLangMovenext=gT("Submit");
$sAccessKeyNext='l';// Why l ?
}else{
$sLangMovenext=gT("Next");
$sAccessKeyNext='n';
}
$sSurveyMover.= CHtml::htmlButton($sLangMovenext,array('type'=>'submit','id'=>"{$sMoveNext}btn",'value'=>$sMoveNext,'name'=>$sMoveNext,'accesskey'=>$sAccessKeyNext,'class'=>$sClass));
}
return $sSurveyMover;
}
/**
* Caculate assessement scores
*
* @param mixed $surveyid
* @param mixed $returndataonly - only returns an array with data
*/
function doAssessment($surveyid, $returndataonly=false)
{
$baselang=Survey::model()->findByPk($surveyid)->language;
if(Survey::model()->findByPk($surveyid)->assessments!="Y")
{
return false;
}
$total=0;
if (!isset($_SESSION['survey_'.$surveyid]['s_lang']))
{
$_SESSION['survey_'.$surveyid]['s_lang']=$baselang;
}
$query = "SELECT * FROM {{assessments}}
WHERE sid=$surveyid and language='".$_SESSION['survey_'.$surveyid]['s_lang']."'
ORDER BY scope, id";
if ($result = dbExecuteAssoc($query)) //Checked
{
$aResultSet=$result->readAll();
if (count($aResultSet) > 0)
{
foreach($aResultSet as $row)
{
if ($row['scope'] == "G")
{
$assessment['group'][$row['gid']][]=array("name"=>$row['name'],
"min"=>$row['minimum'],
"max"=>$row['maximum'],
"message"=>$row['message']);
}
else
{
$assessment['total'][]=array( "name"=>$row['name'],
"min"=>$row['minimum'],
"max"=>$row['maximum'],
"message"=>$row['message']);
}
}
$fieldmap=createFieldMap($surveyid, "full",false,false,$_SESSION['survey_'.$surveyid]['s_lang']);
$i=0;
$total=0;
$groups=array();
foreach($fieldmap as $field)
{
if (in_array($field['type'],array('1','F','H','W','Z','L','!','M','O','P')))
{
$fieldmap[$field['fieldname']]['assessment_value']=0;
if (isset($_SESSION['survey_'.$surveyid][$field['fieldname']]))
{
if (($field['type'] == "M") || ($field['type'] == "P")) //Multiflexi choice - result is the assessment attribute value
{
if ($_SESSION['survey_'.$surveyid][$field['fieldname']] == "Y")
{
$aAttributes=getQuestionAttributeValues($field['qid'],$field['type']);
$fieldmap[$field['fieldname']]['assessment_value']=(int)$aAttributes['assessment_value'];
$total=$total+(int)$aAttributes['assessment_value'];
}
}
else // Single choice question
{
$usquery = "SELECT assessment_value FROM {{answers}} where qid=".$field['qid']." and language='$baselang' and code=".dbQuoteAll($_SESSION['survey_'.$surveyid][$field['fieldname']]);
$usresult = dbExecuteAssoc($usquery); //Checked
if ($usresult)
{
$usrow = $usresult->read();
$fieldmap[$field['fieldname']]['assessment_value']=$usrow['assessment_value'];
$total=$total+$usrow['assessment_value'];
}
}
}
$groups[]=$field['gid'];
}
$i++;
}
$groups=array_unique($groups);
foreach($groups as $group)
{
$grouptotal=0;
foreach ($fieldmap as $field)
{
if ($field['gid'] == $group && isset($field['assessment_value']))
{
//$grouptotal=$grouptotal+$field['answer'];
if (isset ($_SESSION['survey_'.$surveyid][$field['fieldname']]))
{
$grouptotal=$grouptotal+$field['assessment_value'];
}
}
}
$subtotal[$group]=$grouptotal;
}
}
$assessments = "";
if (isset($subtotal) && is_array($subtotal))
{
foreach($subtotal as $key=>$val)
{
if (isset($assessment['group'][$key]))
{
foreach($assessment['group'][$key] as $assessed)
{
if ($val >= $assessed['min'] && $val <= $assessed['max'] && $returndataonly===false)
{
$assessments .= "\t<!-- GROUP ASSESSMENT: Score: $val Min: ".$assessed['min']." Max: ".$assessed['max']."-->
<table class='assessments'>
<tr>
<th>".str_replace(array("{PERC}", "{TOTAL}"), array($val, $total), $assessed['name'])."
</th>
</tr>
<tr>
<td>".str_replace(array("{PERC}", "{TOTAL}"), array($val, $total), $assessed['message'])."
</td>
</tr>
</table><br />\n";
}
}
}
}
}
if (isset($assessment['total']))
{
foreach($assessment['total'] as $assessed)
{
if ($total >= $assessed['min'] && $total <= $assessed['max'] && $returndataonly===false)
{
$assessments .= "\t\t\t<!-- TOTAL ASSESSMENT: Score: $total Min: ".$assessed['min']." Max: ".$assessed['max']."-->
<table class='assessments' align='center'>
<tr>
<th>".str_replace(array("{PERC}", "{TOTAL}"), array($val, $total), stripslashes($assessed['name']))."
</th>
</tr>
<tr>
<td>".str_replace(array("{PERC}", "{TOTAL}"), array($val, $total), stripslashes($assessed['message']))."
</td>
</tr>
</table>\n";
}
}
}
if ($returndataonly==true)
{
return array('total'=>$total);
}
else
{
return $assessments;
}
}
}
/**
* Update SESSION VARIABLE: grouplist
* A list of groups in this survey, ordered by group name.
* @param int surveyid
* @param string language
*/
function UpdateGroupList($surveyid, $language)
{
unset ($_SESSION['survey_'.$surveyid]['grouplist']);
$query = "SELECT * FROM {{groups}} WHERE sid=$surveyid AND language='".$language."' ORDER BY group_order";
$result = dbExecuteAssoc($query) or safeDie ("Couldn't get group list<br />$query<br />"); //Checked
$groupList = array();
foreach ($result->readAll() as $row)
{
$group = array(
'gid' => $row['gid'],
'group_name' => $row['group_name'],
'description' => $row['description']);
$groupList[] = $group;
$gidList[$row['gid']] = $group;
}
if (!Yii::app()->getConfig('previewmode') && isset($_SESSION['survey_'.$surveyid]['groupReMap']) && count($_SESSION['survey_'.$surveyid]['groupReMap'])>0)
{
// Now adjust the grouplist
$groupRemap = $_SESSION['survey_'.$surveyid]['groupReMap'];
$groupListCopy = $groupList;
foreach ($groupList as $gseq => $info) {
$gid = $info['gid'];
if (isset($groupRemap[$gid])) {
$gid = $groupRemap[$gid];
}
$groupListCopy[$gseq] = $gidList[$gid];
}
$groupList = $groupListCopy;
}
$_SESSION['survey_'.$surveyid]['grouplist'] = $groupList;
}
/**
* FieldArray contains all necessary information regarding the questions
* This function is needed to update it in case the survey is switched to another language
* @todo: Make 'fieldarray' obsolete by replacing with EM session info
*/
function UpdateFieldArray()
{
global $surveyid;
if (isset($_SESSION['survey_'.$surveyid]['fieldarray']))
{
foreach ($_SESSION['survey_'.$surveyid]['fieldarray'] as $key => $value)
{
$questionarray = &$_SESSION['survey_'.$surveyid]['fieldarray'][$key];
$query = "SELECT title, question FROM {{questions}} WHERE qid=".$questionarray[0]." AND language='".$_SESSION['survey_'.$surveyid]['s_lang']."'";
$usrow = Yii::app()->db->createCommand($query)->queryRow();
if ($usrow)
{
$questionarray[2]=$usrow['title'];
$questionarray[3]=$usrow['question'];
}
unset($questionarray);
}
}
}
/**
* checkCompletedQuota() returns matched quotas information for the current response
* @param integer $surveyid - Survey identification number
* @param bool $return - set to true to return information, false do the quota
* @return array - nested array, Quotas->Members->Fields, includes quota information matched in session.
*/
function checkCompletedQuota($surveyid,$return=false)
{
if (!isset($_SESSION['survey_'.$surveyid]['srid']))
{
return;
}
static $aMatchedQuotas; // EM call 2 times quotas with 3 lines of php code, then use static.
if(!$aMatchedQuotas)
{
$aMatchedQuotas=array();
$quota_info=$aQuotasInfo = getQuotaInformation($surveyid, $_SESSION['survey_'.$surveyid]['s_lang']);
// $aQuotasInfo have an 'active' key, we don't use it ?
if(!$aQuotasInfo || empty($aQuotasInfo))
return $aMatchedQuotas;
// OK, we have some quota, then find if this $_SESSION have some set
$aPostedFields = explode("|",Yii::app()->request->getPost('fieldnames','')); // Needed for quota allowing update
foreach ($aQuotasInfo as $aQuotaInfo)
{
$iMatchedAnswers=0;
$bPostedField=false;
// Array of field with quota array value
$aQuotaFields=array();
// Array of fieldnames with relevance value : EM fill $_SESSION with default value even is unrelevant (em_manager_helper line 6548)
$aQuotaRelevantFieldnames=array();
foreach ($aQuotaInfo['members'] as $aQuotaMember)
{
$aQuotaFields[$aQuotaMember['fieldname']][] = $aQuotaMember['value'];
$aQuotaRelevantFieldnames[$aQuotaMember['fieldname']]=isset($_SESSION['survey_'.$surveyid]['relevanceStatus'][$aQuotaMember['qid']]) && $_SESSION['survey_'.$surveyid]['relevanceStatus'][$aQuotaMember['qid']];
}
// For each field : test if actual responses is in quota (and is relevant)
foreach ($aQuotaFields as $sFieldName=>$aValues)
{
$bInQuota=isset($_SESSION['survey_'.$surveyid][$sFieldName]) && in_array($_SESSION['survey_'.$surveyid][$sFieldName],$aValues);
if($bInQuota && $aQuotaRelevantFieldnames[$sFieldName])
{
$iMatchedAnswers++;
}
if(in_array($sFieldName,$aPostedFields))// Need only one posted value
$bPostedField=true;
}
// Count only needed quotas
if($iMatchedAnswers==count($aQuotaFields) && ( $aQuotaInfo['action']!=2 || $bPostedField ) )
{
if($aQuotaInfo['qlimit'] == 0){ // Always add the quota if qlimit==0
$aMatchedQuotas[]=$aQuotaInfo;
}else{
$iCompleted=getQuotaCompletedCount($surveyid, $aQuotaInfo['id']);
if(!is_null($iCompleted) && ((int)$iCompleted >= (int)$aQuotaInfo['qlimit'])) // This remove invalid quota and not completed
$aMatchedQuotas[]=$aQuotaInfo;
}
}
}
}
if ($return)
return $aMatchedQuotas;
if(empty($aMatchedQuotas))
return;
// Now we have all the information we need about the quotas and their status.
// We need to construct the page and do all needed action
$aSurveyInfo=getSurveyInfo($surveyid, $_SESSION['survey_'.$surveyid]['s_lang']);
$sTemplatePath=getTemplatePath($aSurveyInfo['template']);
$sClientToken=isset($_SESSION['survey_'.$surveyid]['token'])?$_SESSION['survey_'.$surveyid]['token']:"";
// $redata for templatereplace
$aDataReplacement = array(
'thissurvey'=>$aSurveyInfo,
'clienttoken'=>$sClientToken,
'token'=>$sClientToken,
);
// We take only the first matched quota, no need for each
$aMatchedQuota=$aMatchedQuotas[0];
// If a token is used then mark the token as completed, do it before event : this allow plugin to update token information
$event = new PluginEvent('afterSurveyQuota');
$event->set('surveyId', $surveyid);
$event->set('responseId', $_SESSION['survey_'.$surveyid]['srid']);// We allways have a responseId
$event->set('aMatchedQuotas', $aMatchedQuotas);// Give all the matched quota : the first is the active
App()->getPluginManager()->dispatchEvent($event);
$blocks = array();
foreach ($event->getAllContent() as $blockData)
{
/* @var $blockData PluginEventContent */
$blocks[] = CHtml::tag('div', array('id' => $blockData->getCssId(), 'class' => $blockData->getCssClass()), $blockData->getContent());
}
// Allow plugin to update message, url, url description and action
$sMessage=$event->get('message',$aMatchedQuota['quotals_message']);
$sUrl=$event->get('url',$aMatchedQuota['quotals_url']);
$sUrlDescription=$event->get('urldescrip',$aMatchedQuota['quotals_urldescrip']);
$sAction=$event->get('action',$aMatchedQuota['action']);
$sAutoloadUrl=$event->get('autoloadurl',$aMatchedQuota['autoload_url']);
// Doing the action and show the page
if ($sAction == "1" && $sClientToken)
submittokens(true);
// Construct the default message
$sMessage = templatereplace($sMessage,array(),$aDataReplacement, 'QuotaMessage', $aSurveyInfo['anonymized']!='N', NULL, array(), true );
$sUrl = passthruReplace($sUrl, $aSurveyInfo);
$sUrl = templatereplace($sUrl,array(),$aDataReplacement, 'QuotaUrl', $aSurveyInfo['anonymized']!='N', NULL, array(), true );
$sUrlDescription = templatereplace($sUrlDescription,array(),$aDataReplacement, 'QuotaUrldescription', $aSurveyInfo['anonymized']!='N', NULL, array(), true );
// Construction of default message inside quotamessage class
$sHtmlQuotaMessage = "<div class='quotamessage limesurveycore'>\n";
$sHtmlQuotaMessage.= "\t".$sMessage."\n";
$sHtmlQuotaUrl=($sUrl)? "<a href='".$sUrl."'>".$sUrlDescription."</a>" : "";
// Add the navigator with Previous button if quota allow modification.
if ($sAction == "2")
{
$sQuotaStep= isset($_SESSION['survey_'.$surveyid]['step'])?$_SESSION['survey_'.$surveyid]['step']:0; // Surely not needed
$sNavigator = CHtml::htmlButton(gT("Previous"),array('type'=>'submit','id'=>"moveprevbtn",'value'=>$sQuotaStep,'name'=>'move','accesskey'=>'p','class'=>"submit button"));
//$sNavigator .= " ".CHtml::htmlButton(gT("Submit"),array('type'=>'submit','id'=>"movesubmit",'value'=>"movesubmit",'name'=>"movesubmit",'accesskey'=>'l','class'=>"submit button"));
$sHtmlQuotaMessage.= CHtml::form(array("/survey/index","sid"=>$surveyid), 'post', array('id'=>'limesurvey','name'=>'limesurvey'));
$sHtmlQuotaMessage.= templatereplace(file_get_contents($sTemplatePath."/navigator.pstpl"),array('NAVIGATOR'=>$sNavigator,'SAVE'=>''),$aDataReplacement);
$sHtmlQuotaMessage.= CHtml::hiddenField('sid',$surveyid);
$sHtmlQuotaMessage.= CHtml::hiddenField('token',$sClientToken);// Did we really need it ?
$sHtmlQuotaMessage.= CHtml::endForm();
}
$sHtmlQuotaMessage.= "</div>\n";
// Add the plugin message before default message
$sHtmlQuotaMessage = implode("\n", $blocks) ."\n". $sHtmlQuotaMessage;
// Send page to user and end.
sendCacheHeaders();
if($sAutoloadUrl == 1 && $sUrl != "")
{
if ($sAction == "1")
killSurveySession($surveyid);
header("Location: ".$sUrl);
}
doHeader();
echo templatereplace(file_get_contents($sTemplatePath."/startpage.pstpl"),array(),$aDataReplacement);
echo templatereplace(file_get_contents($sTemplatePath."/completed.pstpl"),array("COMPLETED"=>$sHtmlQuotaMessage,"URL"=>$sHtmlQuotaUrl),$aDataReplacement);
echo templatereplace(file_get_contents($sTemplatePath."/endpage.pstpl"),array(),$aDataReplacement);
doFooter();
if ($sAction == "1")
killSurveySession($surveyid);
Yii::app()->end();
}
/**
* encodeEmail : encode admin email in public part
*
* @param mixed $mail
* @param mixed $text
* @param mixed $class
* @param mixed $params
*/
function encodeEmail($mail, $text="", $class="", $params=array())
{
$encmail ="";
for($i=0; $i<strlen($mail); $i++)
{
$encMod = rand(0,2);
switch ($encMod)
{
case 0: // None
$encmail .= substr($mail,$i,1);
break;
case 1: // Decimal
$encmail .= "&#".ord(substr($mail,$i,1)).';';
break;
case 2: // Hexadecimal
$encmail .= "&#x".dechex(ord(substr($mail,$i,1))).';';
break;
}
}
if(!$text)
{
$text = $encmail;
}
return $text;
}
/**
* GetReferringUrl() returns the referring URL
* @return string
*/
function GetReferringUrl()
{
// read it from server variable
if(isset($_SERVER["HTTP_REFERER"]))
{
if (!Yii::app()->getConfig('strip_query_from_referer_url'))
{
return $_SERVER["HTTP_REFERER"];
}
else
{
$aRefurl = explode("?",$_SERVER["HTTP_REFERER"]);
return $aRefurl[0];
}
}
else
{
return null;
}
}
/**
* Shows the welcome page, used in group by group and question by question mode
*/
function display_first_page() {
global $token, $surveyid, $thissurvey, $navigator;
$totalquestions = $_SESSION['survey_'.$surveyid]['totalquestions'];
// Fill some necessary var for template
$navigator = surveymover();
$sitename = Yii::app()->getConfig('sitename');
$languagechanger=makeLanguageChangerSurvey(App()->language);
sendCacheHeaders();
doHeader();
LimeExpressionManager::StartProcessingPage();
LimeExpressionManager::StartProcessingGroup(-1, false, $surveyid); // start on welcome page
$redata = compact(array_keys(get_defined_vars()));
$sTemplatePath=$_SESSION['survey_'.$surveyid]['templatepath'];
echo templatereplace(file_get_contents($sTemplatePath."startpage.pstpl"),array(),$redata,'frontend_helper[2757]');
echo CHtml::form(array("/survey/index","sid"=>$surveyid), 'post', array('id'=>'limesurvey','name'=>'limesurvey','autocomplete'=>'off'));
echo "\n\n<!-- START THE SURVEY -->\n";
echo templatereplace(file_get_contents($sTemplatePath."welcome.pstpl"),array(),$redata,'frontend_helper[2762]')."\n";
if ($thissurvey['anonymized'] == "Y")
{
echo templatereplace(file_get_contents($sTemplatePath."/privacy.pstpl"),array(),$redata,'frontend_helper[2765]')."\n";
}
echo templatereplace(file_get_contents($sTemplatePath."navigator.pstpl"),array(),$redata,'frontend_helper[2767]');
if ($thissurvey['active'] != "Y")
{
echo "<p style='text-align:center' class='error'>".gT("This survey is currently not active. You will not be able to save your responses.")."</p>\n";
}
echo "\n<input type='hidden' name='sid' value='$surveyid' id='sid' />\n";
if (isset($token) && !empty($token)) {
echo "\n<input type='hidden' name='token' value='$token' id='token' />\n";
}
echo "\n<input type='hidden' name='lastgroupname' value='_WELCOME_SCREEN_' id='lastgroupname' />\n"; //This is to ensure consistency with mandatory checks, and new group test
$loadsecurity = returnGlobal('loadsecurity',true);
if (isset($loadsecurity)) {
echo "\n<input type='hidden' name='loadsecurity' value='$loadsecurity' id='loadsecurity' />\n";
}
$_SESSION['survey_'.$surveyid]['LEMpostKey'] = mt_rand();
echo "<input type='hidden' name='LEMpostKey' value='{$_SESSION['survey_'.$surveyid]['LEMpostKey']}' id='LEMpostKey' />\n";
echo "<input type='hidden' name='thisstep' id='thisstep' value='0' />\n";
echo "\n</form>\n";
echo templatereplace(file_get_contents($sTemplatePath."endpage.pstpl"),array(),$redata,'frontend_helper[2782]');
echo LimeExpressionManager::GetRelevanceAndTailoringJavaScript();
LimeExpressionManager::FinishProcessingPage();
doFooter();
}
/**
* killSurveySession : reset $_SESSION part for the survey
* @param int $iSurveyID
*/
function killSurveySession($iSurveyID)
{
// Unset the session
unset($_SESSION['survey_'.$iSurveyID]);
// Force EM to refresh
LimeExpressionManager::SetDirtyFlag();
}
/**
* Resets all question timers by expiring the related cookie - this needs to be called before any output is done
* @todo Make cookie survey ID aware
*/
function resetTimers()
{
$cookie=new CHttpCookie('limesurvey_timers', '');
$cookie->expire = time()- 3600;
Yii::app()->request->cookies['limesurvey_timers'] = $cookie;
}
/**
* Set the public survey language
* Control if language exist in this survey, else set to survey default language
* if $surveyid <= 0 : set the language to default site language
* @param int $surveyid
* @param string $language
*/
function SetSurveyLanguage($surveyid, $sLanguage)
{
$surveyid=sanitize_int($surveyid);
$default_language = Yii::app()->getConfig('defaultlang');
if (isset($surveyid) && $surveyid>0)
{
$default_survey_language= Survey::model()->findByPk($surveyid)->language;
$additional_survey_languages = Survey::model()->findByPk($surveyid)->getAdditionalLanguages();
if (!isset($sLanguage) || ($sLanguage=='')
|| !( in_array($sLanguage,$additional_survey_languages) || $sLanguage==$default_survey_language)
)
{
// Language not supported, fall back to survey's default language
$_SESSION['survey_'.$surveyid]['s_lang'] = $default_survey_language;
} else {
$_SESSION['survey_'.$surveyid]['s_lang'] = $sLanguage;
}
App()->setLanguage($_SESSION['survey_'.$surveyid]['s_lang']);
$thissurvey=getSurveyInfo($surveyid, @$_SESSION['survey_'.$surveyid]['s_lang']);
Yii::app()->loadHelper('surveytranslator');
LimeExpressionManager::SetEMLanguage($_SESSION['survey_'.$surveyid]['s_lang']);
}
else
{
if(!$sLanguage)
{
$sLanguage=$default_language;
}
$_SESSION['survey_'.$surveyid]['s_lang'] = $sLanguage;
App()->setLanguage($_SESSION['survey_'.$surveyid]['s_lang']);
}
}
/**
* getMove get move button clicked
**/
function getMove()
{
#
$aAcceptedMove=array('default','movenext','movesubmit','moveprev','saveall','loadall','clearall','changelang');
// We can control is save and load are OK : todo fix according to survey settings
// Maybe allow $aAcceptedMove in Plugin
$move=Yii::app()->request->getParam('move');
foreach($aAcceptedMove as $sAccepteMove)
{
if(Yii::app()->request->getParam($sAccepteMove))
$move=$sAccepteMove;
}
if($move=='clearall' && App()->request->getPost('confirm-clearall')!='confirm'){
$move="clearcancel";
}
if($move=='default')
{
$surveyid=Yii::app()->getConfig('surveyID');
$thissurvey=getsurveyinfo($surveyid);
$iSessionStep=(isset($_SESSION['survey_'.$surveyid]['step']))?$_SESSION['survey_'.$surveyid]['step']:false;
$iSessionTotalSteps=(isset($_SESSION['survey_'.$surveyid]['totalsteps']))?$_SESSION['survey_'.$surveyid]['totalsteps']:false;
if ($iSessionStep && ($iSessionStep == $iSessionTotalSteps)|| $thissurvey['format'] == 'A')
{
$move="movesubmit";
}
else
{
$move="movenext";
}
}
return $move;
}
| code |
नवजोत कौर और गुरजीत कौर के गोल की मदद से भारतीय महिला हॉकी टीम ने इंग्लैंड दौरे के अपने आखिरी मैच में ब्रिटेन को २-२ से ड्रॉ पर रोका। भारत के लिए नवजोत (आठवां मिनट) और गुरजीत (४८वां मिनट) ने गोल दागे जबकि ब्रिटेन के लिए एलिजाबेथ नील (५५वां) और अन्ना टोमान (६०वें मिनट) ने गोल किए। इसके साथ ही भारतीय टीम ने दौरे का अंत ब्रिटेन जैसी मजबूत टीम के खिलाफ ड्रॉ के साथ किया। भारत ने पांच मैचों में से एक जीता, एक हारा और तीन ड्रॉ खेले।
पिछले मैच में पराजय का सामना करने वाली भारतीय टीम ने आक्रामक शुरुआत की और मेजबान के हाफ में ही खेल होता रहा। शुरुआती हमलों का फायदा आठवें मिनट में पेनल्टी कॉर्नर के रूप में मिला जिसे नवजोत ने गोल में बदला। दूसरे क्वॉर्टर में दोनों टीमों के बीच मुकाबला बराबरी का रहा। ब्रिटेन को तीन पेनल्टी कॉर्नर मिले लेकिन भारतीय गोलकीपर सविता ने तीनों को बचा लिया।
पढ़ें, महिला हॉकी : ग्रेट ब्रिटेन ने भारत को ३-१ से हराया
तीसरे क्वार्टर में भारत ने गेंद पर नियंत्रण बनाए रखा। हाफटाइम में हीश की जगह आई एमी टिनेंट ने ४०वें मिनट में गुरजीत का गोल बचाया। भारत ने ४८वें मिनट में एक और गोल किया। ब्रिटेन ने हालांकि आखिरी पांच मिनट में दो गोल करके भारतीय टीम के जीत के मंसूबों पर पानी फेर दिया। यह भारतीय गोलकीपर सविता का २००वां अंतरराष्ट्रीय मैच था। | hindi |
\begin{document}
\newtheorem{theorem}{Theorem}[section]
\newtheorem{proposition}[theorem]{Proposition}
\newtheorem{corollary}[theorem]{Corollary}
\newtheorem{lemma}[theorem]{Lemma}
\title{Five-Collinear Sierpinski Gasket is\Not Self-Similar}
\begin{abstract}
A geometrical conclusion: Sierpinski gasket, two Sierpinski gaskets in a line, three Sierpinski gaskets in a line, and four Sierpinski gaskets in a line are self-similar, but five Sierpinski gaskets in a line is not, which is proved in this paper.
\end{abstract}
\section{Introduction}
Sierpinski gasket, two Sierpinski gaskets in a line, three Sierpinski gaskets in a line, and four Sierpinski gaskets in a line are the attractor of some contractive IFS consisting of similitudes, but five Sierpinski gaskets in a line is not. The proof is based on induction. Five Sierpinski gaskets in a line is of fractal dimension, which makes the situation a little bit complicated. The idea of the proof is to use figures of similar shapes with five Sierpinski gaskets in a line, but of integral dimension, to analyze properties of five Sierpinski gaskets in a line.
\section{Notations And Definitions}
\subsection{Notations}
\textbf{$\mathbb{Z}$} = $\{\dots, -2, -1, 0, 1, 2, \dots \}$.\\
\textbf{$\mathbb{N}$} = $\{0, 1, 2, \dots \}$.\\
\textbf{$\mathbb{N}_+$} = $\{1, 2, \dots \}$.\\
\textbf{$\blacktriangle P_i P_j P_k$}: The solid triangle in $\mathbb{R}^2$ with vertices $P_i$, $P_j$, and $P_k$.\\
\\
Below, let $A$, $B$ be sets and $f$, $g$ be maps:\\
\textbf{$d(x,y)$}: The distance between point $x$ and point $y$.\\
\textbf{$A-B$} = $\{x\mid x\in A, x\not\in B\}$.\\
\textbf{$diam(A)$} = $\sup_{x\in A, y\in A}\{d(x,y)\}$, where $A$ is a nonempty subset in $\mathbb{R}^2$.\\
\textbf{$d(A,B)$} = $\inf_{x\in A, y\in B}\{d(x,y)\}$, where $A$, $B$ are nonempty subsets in $\mathbb{R}^2$.\\
\textbf{$f\circ g$}: The composition of $f$ and $g$, which maps $x$ to $f(g(x))$.\\
\textbf{$f^{\circ k}$}: The composition of $k$ $f$'s ($k\in \mathbb{Z}$).
\subsection{Definitions}
\label{def}
\textbf{Similitude}: a map $\mathbb{R}^2\to \mathbb{R}^2$ which is the composition of scaling, rotation, translation, and maybe reflection. That is, $f$ is a similitude if and only if there exist $\theta \in [0,2\pi), k \in (0, +\infty)$ and $x_0, y_0\in \mathbb{R}$, such that
\begin{displaymath}
f{x \choose y}=k
\left( \begin{array}{cc}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{array} \right)
{x \choose y} + {x_0 \choose y_0}
\end{displaymath}
or
\begin{displaymath}
f{x \choose y}=k
\left( \begin{array}{cc}
\cos\theta & \sin\theta \\
\sin\theta & -\cos\theta
\end{array} \right)
{x \choose y} + {x_0 \choose y_0},
\end{displaymath}
where $k$ is called the \textbf{scaling factor} of the similitude. If $k$ is strictly less than $1$, then the similitude is called $\textbf{contractive}$.\\
\textbf{IFS}(Iterated Function System)\cite{Hutchinson}: $F=\{ \mathbb{R}^2;f_1,f_2,\cdots,f_n\}$, where $f_1,f_2,\cdots,f_n:\mathbb{R}^2\to \mathbb{R}^2$ are continuous maps.\\
\textbf{Contractive IFS consisting of similitudes}: $F=\{ \mathbb{R}^2;f_1,f_2,\cdots,f_n\}$, where $f_1,f_2,\cdots,f_n:\mathbb{R}^2\to \mathbb{R}^2$ are contractive similitudes.\\
\textbf{Sierpinski gasket}: The attracor of the IFS $F=\{\mathbb{R}^2;
f_1{x \choose y}=
\left( \begin{array}{cc}
\frac{1}{2} & 0 \\
0 & \frac{1}{2}
\end{array} \right)
{x \choose y}, \\
f_2{x \choose y}=
\left( \begin{array}{cc}
\frac{1}{2} & 0 \\
0 & \frac{1}{2}
\end{array} \right)
{x \choose y}+{\frac{1}{4} \choose \frac{\sqrt{3}}{4}},
f_3{x \choose y}=
\left( \begin{array}{cc}
\frac{1}{2} & 0 \\
0 & \frac{1}{2}
\end{array} \right)
{x \choose y} + {\frac{1}{2} \choose 0}\}$ (see Figure \ref{figure1}).
\begin{center}
\makeatletter\deffigure{figure}\makeatother
\scalebox{0.15}{\includegraphics{figure_1.png}}
\caption{Sierpinski gasket}\label{figure1}
\end{center}
\textbf{Two-Sierpinski}: The union of Sierpinski gasket and Sierpinski gasket translated along positive $x$ axis by $1$ unit (see Figure \ref{figure2}).
\begin{center}
\makeatletter\deffigure{figure}\makeatother
\scalebox{0.17}{\includegraphics{figure_2.png}}
\caption{Two-Sierpinski}\label{figure2}
\end{center}
\textbf{$N$-Sierpinski}: The union of $(n-1)$-Sierpinski and Sierpinski gasket translated along positive $x$ axis by $n-1$ unit (see Figure \ref{figure3} when $n=3$). Five-Sierpinski will be denoted by \textbf{$E$} in this paper (see Figure \ref{figure4}). Let \textbf{$C$} be the figure obtained from Sierpinski gasket dilated by factor $8$. Then $E \subset C$ (see Figure \ref{figure5}, the whole figure is $C$, and the brown part is $E$).
\begin{center}
\makeatletter\deffigure{figure}\makeatother
\scalebox{0.25}{\includegraphics{figure_3.png}}
\caption{Three-Sierpinski}\label{figure3}
\end{center}
\begin{center}
\makeatletter\deffigure{figure}\makeatother
\scalebox{0.27}{\includegraphics{figure_4.png}}
\caption{Five-Sierpinski (denoted by $E$)}\label{figure4}
\end{center}
\begin{center}
\makeatletter\deffigure{figure}\makeatother
\scalebox{0.2}{\includegraphics{figure_5.png}}
\caption{Five-Sierpinski (denoted by $E$) inside Sierpinski gasket dilated by factor $8$ (denoted by $C$)}\label{figure5}
\end{center}
\textbf{Figures $A_n$ and $B_n$} ($n\in \mathbb{Z}$ and $n \ge -3$): Since $C$ is a ``bigger'' version of Sierpinski gasket, it can be constructed as the intersection of a sequence of sets, the first four of which are listed in Figure \ref{figure6}. Denote this sequence of sets by $A_n$ ($n\in \mathbb{Z}$ and $n \ge -3$). Notice each $A_n$ is the union of $3^{n+3}$ solid equilateral triangles of the same size, whose topological interiors are disjoint each other. Denote the union of all vertices of these solid equilateral triangles by $B_n$ ($n\in \mathbb{Z}$ and $n \ge -3$), the first four of which are listed in Figure \ref{figure7}.
\begin{center}
\makeatletter\deffigure{figure}\makeatother
\scalebox{0.7}{\includegraphics{figure_6.png}}
\caption{$A_{-3}$, $A_{-2}$, $A_{-1}$, and $A_{0}$}\label{figure6}
\end{center}
\begin{center}
\makeatletter\deffigure{figure}\makeatother
\scalebox{0.2}{\includegraphics{figure_7.png}}
\caption{$B_{-3}$, $B_{-2}$, $B_{-1}$, and $B_{0}$}\label{figure7}
\end{center}
\textbf{Map $T$}: $\mathbb{R}^2 \to \mathbb{R}^2$,
\begin{equation}\label{def t}
T{x \choose y}=\frac{1}{2}
\left( \begin{array}{cc}
\cos\frac{2\pi}{3} & -\sin\frac{2\pi}{3} \\
\sin\frac{2\pi}{3} & \cos\frac{2\pi}{3}
\end{array} \right)
{x \choose y} + {\frac{3}{4} \choose \frac{\sqrt{3}}{4}}.
\end{equation}
Then $T$ is a contractive similitude with scaling factor $\frac{1}{2}$ and $T$ is bijective.
\section{Key Theorem}
As indicated in Figure \ref{figure1}, Figure \ref{figure2}, and Figure \ref{figure3}, Sierpinski gasket, two-Sierpinski, and three-Sierpinski are the attractor of some contractive IFS consisting of similitudes. These IFSs can be constructed as follows. In each figure, find similitudes that can map the whole figure to a region of the same colour. The number of similitudes is the number of different colours. Then the desired IFS is constructed by these similitudes. We can also construct a contractive IFS consisting of similitudes having four-Sierpinski as its attractor. This case is similar to three-Sierpinski.
However, as indicated in the following theorem, five-Sierpinski cannot be the attractor of any contractive IFS consisting of similitudes.
\begin{theorem}\label{theorem1}
Five-Sierpinski is not the attractor of any contractive IFS consisting of similitudes.
\end{theorem}
The proof of this theorem needs several lemmas.
\begin{lemma}\label{lemma1}
Denote five-Sierpinski by $E$. If $f$ is a similitude with scaling factor $k\le \frac{1}{80}$ such that $f(E)\subset E$ and $f(E)\cap \blacktriangle P_6 P_7 P_8 \neq \emptyset$ (see Figure \ref{figure4}), then $f(E)\subset \blacktriangle P_1 P_4 P_5 \cap E$. Further more, $T^{-1}(f(E))\subset \blacktriangle P_1 P_2 P_3 \cap E \subset E$.
\end{lemma}
\begin{proof}
First observe that $diam(E)=5$. Since $f$ is a similitude, for any $x,y\in \mathbb{R}^2$, $d(f(x),f(y))=k d(x,y)$. So, $diam(f(E))=\sup_{x\in f(E),y\in f(E)}\{d(x,y)\}=\sup_{x\in E,y\in E}\{d(f(x),f(y))\}=\sup_{x\in E,y\in E}\{k d(x,y)\}=k \sup_{x\in E,y\in E}\{d(x,y)\}=k\cdot diam(E)\le \frac{5}{80}=\frac{1}{16}$.
As $f(E)\cap \blacktriangle P_6 P_7 P_8 \neq \emptyset$, suppose $x_0 \in f(E)\cap \blacktriangle P_6 P_7 P_8$. Then, for all $x_1 \in f(E)$, $d(x_1,x_0)\le diam(f(E))=\frac{1}{16}$. Since $d(\blacktriangle P_6 P_7 P_8 , E-\blacktriangle P_1 P_4 P_5)=\frac{\sqrt{3}}{16}$, for all $x_2 \in (E-\blacktriangle P_1 P_4 P_5 )$, we have $d(x_2,x_0)\ge \frac{\sqrt{3}}{16}$. So, $f(E) \cap (E-\blacktriangle P_1 P_4 P_5 )= \emptyset$. Now, $f(E)\subset E$, so $f(E)\subset \blacktriangle P_1 P_4 P_5 \cap E$.
Since $\blacktriangle P_1 P_4 P_5 \cap E\subset T(E)$ ($T$ is defined in \ref{def t}), $f(E)\subset \blacktriangle P_1 P_4 P_5 \cap T(E)$. So, $T^{-1}(f(E))\subset T^{-1}(\blacktriangle P_1 P_4 P_5 \cap T(E))=T^{-1}(\blacktriangle P_1 P_4 P_5 )\cap E=\blacktriangle P_1 P_2 P_3 \cap E \subset E$.
\end{proof}
\begin{lemma}\label{lemma2}
Denote five-Sierpinski by $E$. If $f$ is a contractive similitude such that $f(E)\subset E$, then there exists $m\in \mathbb{N}_+$ such that the scaling factor of $f$ is $\frac{1}{2^m}$ and $f(P_1),f(P_2),f(P_3)\in B_m$ (See Figure \ref{figure4} and Figure \ref{figure7}).
\end{lemma}
\begin{proof}
As you can see in Figure \ref{figure5}, $E\subset C$, so $f(E)\subset E\subset C$. Because $C=\cap^{\infty}_{n=-3}A_n$, $f(E)\subset A_n$ for all $n\in \{ -3,-2,-1,0,\cdots \}$.
Each $A_n$ is the union of $3^{n+3}$ solid equilateral triangles of the same size, whose topological interiors are disjoint each other (see Figure \ref{figure6}). Consider three points $f(P_1),f(P_2),f(P_3)$. Now $f(P_1),f(P_2),f(P_3)$ are different points since $f$ is bijective. They are either in the same solid triangle or not. Suppose $N$ is the greatest integer in $\{ -3,-2,-1,0,\cdots \}$ such that $f(P_1),f(P_2),f(P_3)$ are in the same solid triangle of $A_N$ (note that such $N$ exists because $f(P_1),f(P_2),f(P_3)$ have positive distance each other and the diameter of solid triangles of $A_n$ tends to $0$ as $n$ tends to $\infty$). Then $f(P_1),f(P_2),f(P_3)$ are not in the same solid triangle of $A_{N+1}$.
Suppose $\blacktriangle Q_1 Q_4 Q_6$ is the solid triangle of $A_N$ where $f(P_1),f(P_2),f(P_3)$ are in (see Figure \ref{figure8}). Then $\blacktriangle Q_1 Q_2 Q_3$, $\blacktriangle Q_2 Q_4 Q_5$, $\blacktriangle Q_3 Q_5 Q_6$ are solid triangles of $A_{N+1}$. So $f(P_1),f(P_2),f(P_3)$ are not in the same one of $\blacktriangle Q_1 Q_2 Q_3$, $\blacktriangle Q_2 Q_4 Q_5$, $\blacktriangle Q_3 Q_5 Q_6$.
\begin{center}
\makeatletter\deffigure{figure}\makeatother
\scalebox{1}{\includegraphics{figure_8.png}}
\caption{$\blacktriangle Q_1 Q_4 Q_6$}\label{figure8}
\end{center}
Suppose two of $f(P_1),f(P_2),f(P_3)$ are in the same one of $\blacktriangle Q_1 Q_2 Q_3$, $\blacktriangle Q_2 Q_4 Q_5$, $\blacktriangle Q_3 Q_5 Q_6$ and the other one of $f(P_1),f(P_2),f(P_3)$ is in another one of $\blacktriangle Q_1 Q_2 Q_3$, $\blacktriangle Q_2 Q_4 Q_5$, $\blacktriangle Q_3 Q_5 Q_6$. Without loss of generality, suppose $f(P_1),f(P_2)\in \blacktriangle Q_2 Q_4 Q_5$ and $f(P_3)\in \blacktriangle Q_3 Q_5 Q_6$. Since $f$ is a similitude, $f$ maps straight lines to straight lines. Because $f(E)\subset A_{N+1}$, $f$ maps segment $P_1 P_3$ to a segment in $A_{N+1}$ and maps segment $P_2 P_3$ to another segment in $A_{N+1}$. Now, segment $f(P_1)f(P_3)\subset A_{N+1}$ and segment $f(P_2)f(P_3)\subset A_{N+1}$.
If $f(P_3)=Q_3$, then $f(P_1)=Q_2$ and $f(P_2)=Q_5$, or $f(P_1)=Q_5$ and $f(P_2)=Q_2$. Both cases are impossible since $f(P_8)\in f(E)\subset A_{N+1}$ (see Figure \ref{figure4} for $P_8$). If $f(P_3)\neq Q_3$, then $f(P_1),f(P_2),f(P_3)$ are in segment $Q_4 Q_6$, which is also impossible.
Therefore, $f(P_1),f(P_2),f(P_3)$ are in different ones of $\blacktriangle Q_1 Q_2 Q_3$, $\blacktriangle Q_2 Q_4 Q_5$, $\blacktriangle Q_3 Q_5 Q_6$. Without loss of generality, suppose $f(P_1)\in \blacktriangle Q_1 Q_2 Q_3$, $f(P_2)\in \blacktriangle Q_2 Q_4 Q_5$, $f(P_3)\in \blacktriangle Q_3 Q_5 Q_6$. Then, using similar arguments as above, we can prove $f(P_1)=Q_1$, $f(P_2)=Q_4$, $f(P_3)=Q_6$.
Now, the scaling factor of $f$ is $\frac{1}{2^N}$ and $f(P_1),f(P_2),f(P_3)\in B_N$. As $f$ is contractive, $N\ge 1$. So, the lemma is proved.
\end{proof}
\begin{lemma}\label{lemma3}
For all $k\in \mathbb{N}_+$,
$$T^{\circ (k+1)}(\blacktriangle P_6 P_7 P_8)\subset T^{\circ k}(\blacktriangle P_6 P_7 P_8)\subset \cdots \subset \blacktriangle P_6 P_7 P_8$$ and
$$T^{\circ (k+1)}(\blacktriangle P_6 P_7 P_8 \cap E)\subset T^{\circ k}(\blacktriangle P_6 P_7 P_8 \cap E)\subset \cdots \subset \blacktriangle P_6 P_7 P_8 \cap E.$$
\end{lemma}
\begin{proof}
First observe that $T(\blacktriangle P_6 P_7 P_8)\subset \blacktriangle P_6 P_7 P_8$. For all $k\in \mathbb{N}_+$, by applying $T$, $T^{\circ 2}$, $\cdots$, $T^{\circ k}$ to both sides of this relation respectively, we have $T^{\circ 2}(\blacktriangle P_6 P_7 P_8)\subset T(\blacktriangle P_6 P_7 P_8)$, $T^{\circ 3}(\blacktriangle P_6 P_7 P_8)\subset T^{\circ 2}(\blacktriangle P_6 P_7 P_8)$, $\cdots$, $T^{\circ (k+1)}(\blacktriangle P_6 P_7 P_8)\subset T^{\circ k}(\blacktriangle P_6 P_7 P_8)$. Thus, $T^{\circ (k+1)}(\blacktriangle P_6 P_7 P_8)\subset T^{\circ k}(\blacktriangle P_6 P_7 P_8)\subset \cdots \subset \blacktriangle P_6 P_7 P_8$.
Similarly, since $T(\blacktriangle P_6 P_7 P_8 \cap E)\subset \blacktriangle P_6 P_7 P_8 \cap E$, we have $T^{\circ (k+1)}(\blacktriangle P_6 P_7 P_8 \cap E)\subset T^{\circ k}(\blacktriangle P_6 P_7 P_8 \cap E)\subset \cdots \subset \blacktriangle P_6 P_7 P_8 \cap E$.
\end{proof}
\begin{lemma}\label{lemma4}
If $f$ is a contractive similitude such that $f(E)\subset E$ and the scaling factor of $f$ is $\frac{1}{2^m}$ for some $m\in \mathbb{N}_+$, then $T^{\circ m}(\blacktriangle P_6 P_7 P_8)\cap f(E)=\emptyset$.
\end{lemma}
\begin{proof}
When $m\le 6$, according to Lemma \ref{lemma2}, $f(P_1),f(P_2),f(P_3)\in B_m$. Since $f$ is a similitude in $\mathbb{R}^2$, it is uniquely determined by the images of three noncollinear points $P_1,P_2,P_3$. As $f(P_1),f(P_2),f(P_3)\in B_m$ and $B_m$ consists of finitely many points, the possible choices of $f(P_1),f(P_2),f(P_3)$ are finite. So, the possible choices of $f$ are finite. Check directly among all possible choices of $f$ and find the statement $T^{\circ m}(\blacktriangle P_6 P_7 P_8)\cap f(E)=\emptyset$ always holds.
For any integer $M\ge 6$, suppose the lemma holds when $m=M$. When $m=M+1$, $f$ has scaling factor $\frac{1}{2^m}=\frac{1}{2^{M+1}}\le \frac{1}{2^7}\le \frac{1}{80}$.
If $f(E)\cap \blacktriangle P_6 P_7 P_8 =\emptyset$, then the lemma is proved since $T^{\circ m}(\blacktriangle P_6 P_7 P_8)\subset \blacktriangle P_6 P_7 P_8$.
If $f(E)\cap \blacktriangle P_6 P_7 P_8 \neq \emptyset$, then according to Lemma \ref{lemma1}, $T^{-1}(f(E))\subset E$. Let $g=T^{-1}\circ f$. Then $g$ is a contractive similitude such that $g(E)\subset E$ and the scaling factor of $g$ is $\frac{1}{2^{m-1}}=\frac{1}{2^M}$. By the hypothesis, $T^{\circ M}(\blacktriangle P_6 P_7 P_8)\cap g(E)=\emptyset$. Since $T$ is bijective, $T^{\circ m}(\blacktriangle P_6 P_7 P_8)\cap f(E)=T^{\circ (M+1)}(\blacktriangle P_6 P_7 P_8)\cap T(g(E))=T(T^{\circ M}(\blacktriangle P_6 P_7 P_8)\cap g(E))=T(\emptyset)=\emptyset$.
The lemma is proved by induction.
\end{proof}
\begin{lemma}\label{lemma4'}
If $f$ is a contractive similitude such that $f(E)\subset E$, then there exists $K\in \mathbb{N}_+$ such that $T^{\circ K}(\blacktriangle P_6 P_7 P_8)\cap f(E)=\emptyset$.
\end{lemma}
\begin{proof}
Suppose $f$ has scaling factor $k$. According to Lemma \ref{lemma2}, there exists $m\in \mathbb{N}_+$ such that $k=\frac{1}{2^m}$. According to Lemma \ref{lemma4}, $T^{\circ m}(\blacktriangle P_6 P_7 P_8)\cap f(E)=\emptyset$. Let $K=m$ and the lemma is proved.
\end{proof}
\begin{lemma}\label{lemma4''}
If $f$ is a contractive similitude such that $f(E)\subset E$, then there exists $K\in \mathbb{N}_+$ such that for all $k\ge K$, $T^{\circ k}(\blacktriangle P_6 P_7 P_8)\cap f(E)=\emptyset$.
\end{lemma}
\begin{proof}
This lemma is proved directly from Lemma \ref{lemma3} and Lemma \ref{lemma4'}.
\end{proof}
Now, let's prove the key theorem.
\begin{proof}[Proof of Theorem \ref{theorem1}]
Suppose there exists a contractive IFS $F=\{\mathbb{R}^2 ;f_1 ,f_2 ,\cdots ,f_n \}$ ($f_1 ,f_2 ,\cdots ,f_n$ are contractive similitudes) such that $E$ is the attractor of $F$. Then $f_1(E)\cup f_2(E)\cup \cdots \cup f_n(E)=E$. So, for all $m=1,2,\cdots ,n$, $f_m(E)\subset E$. According to Lemma \ref{lemma4''}, there exist $K_m \in \mathbb{N}_+$ such that for all $k\ge K_m$, $T^{\circ k}(\blacktriangle P_6 P_7 P_8)\cap f_m(E)=\emptyset$. Let $K=\max \{K_1,K_2,\cdots K_n\}$. Then for all $m=1,2,\cdots ,n$, $T^{\circ K}(\blacktriangle P_6 P_7 P_8)\cap f_m(E)=\emptyset$. So, $T^{\circ K}(\blacktriangle P_6 P_7 P_8)\cap (f_1(E)\cup f_2(E)\cup \cdots \cup f_n(E))=\emptyset$, or
\begin{equation}
T^{\circ K}(\blacktriangle P_6 P_7 P_8)\cap E=\emptyset.\label{theorem1 eq1}
\end{equation}
According to Lemma \ref{lemma3}, $T^{\circ K}(\blacktriangle P_6 P_7 P_8 \cap E)\subset \blacktriangle P_6 P_7 P_8 \cap E\subset E$. Since $\blacktriangle P_6 P_7 P_8 \cap E\neq \emptyset$, $T^{\circ K}(\blacktriangle P_6 P_7 P_8 \cap E)\neq \emptyset$. Thus, $T^{\circ K}(\blacktriangle P_6 P_7 P_8 \cap E) \cap E=T^{\circ K}(\blacktriangle P_6 P_7 P_8 \cap E)\neq \emptyset$. As $T^{\circ K}(\blacktriangle P_6 P_7 P_8 \cap E)\subset T^{\circ K}(\blacktriangle P_6 P_7 P_8)$, $T^{\circ K}(\blacktriangle P_6 P_7 P_8)\cap E\neq \emptyset$, which contradicts \ref{theorem1 eq1}.
The contradiction implies five-Sierpinski is not the attractor of any contractive IFS consisting of similitudes.
\end{proof}
\end{document} | math |
हनुमा विहारी को इस कारण से भारत के टेस्ट टीम का प्रमुख खिलाड़ी बना लिया गया है
होम > न्यूज़ > हनुमा विहारी की टीम इंडिया में जगह हुई पक्की, इस वजह से विराट चाहते हुए भी नहीं कर सकते नजरअंदाज
भारतीय टीम के युवा बल्लेबाज हनुमा विहारी ने वेस्टइंडीज के खिलाफ पहले टेस्ट में शानदार बल्लेबाजी की प्लेइंग इलेवन में रोहित शर्मा और हनुमा विहारी में किसी एक को ही मौका मिल सकता था और टीम मैनेजमेंट ने विहारी को मौका देना का फैसला किया. इसकी वजह थी कि वह जरूरत पड़ने पर कुछ ओवर की गेंदबाजी भी कर सकते थे.
मनन वोहरा के कारण हनुमा विहारी को टीम में मिली जगह
हनुमा विहारी अंडर-१९ विश्व कप २०१२ में भारतीय टीम का हिस्सा थे. इस टीम ने ऑस्ट्रेलिया को हराकर विश्व कप भी अपने नाम किया था हालाँकि, विहारी टीम में चुने जाने की पहली पसंद नहीं थे.
किंग्स इलेवन पंजाब समेत आईपीएल की कई टीमों के लिए खेल चुके मनन वोहरा की जगह उन्हें विश्व कप टीम में जगह मिली थी. वोहरा ने अपना अंगूठा चोटिल कर लिया था और इसके बाद विहारी को विश्व कप खेलने का मौका मिल गया.
किस्मत ने दिया हरदम से साथ
अपने डेब्यू टेस्ट में ही इंग्लैंड के खिलाफ उन्होंने तीन विकेट लिए थे. इसमें अंतिम टेस्ट खेल रहे एलिस्टर कुक का भी विकेट शामिल था.
ऑस्ट्रेलिया में सलामी बल्लेबाजों के फ्लॉप होने के बाद उन्होंने बॉक्सिंग डे टेस्ट में पारी की शुरुआत की थी और ६८ गेंदों का सामना करके ८ ही रन बनाये लेकिन नये गेंद के खिलाफ खड़े रहने के लिए कप्तान विराट ने उनकी जमकर तारीफ की थी.
हनुमा विहारी बन गए टीम के प्रमुख खिलाड़ी
विहारी हाल ही में एंटीगुआ में वेस्टइंडीज के खिलाफ पहले टेस्ट में एक बार फिर अपनी टीम के बचाव में आए. दोनों पारियों में, उन्होंने भारत को हार से बचाया और अजिंक्य रहाणे के साथ उपयोगी साझेदारी की. उन्होंने पहले ३२ रन बनाकर रहाणे के साथ ८२ रन जोड़े (८१) और फिर ९३ के साथ दूसरे निबंध में रहाणे (१०२) के साथ १३५ रन जोड़े.
उनके पास अपने पहले टेस्ट शतक को दर्ज करने का एक शानदार मौका था, लेकिन टीम के स्कोरिंग में तेजी लाने की कोशिश करते हुए, वह अपना विकेट दे बैठे, अंतरराष्ट्रीय क्रिकेट में अपना पहला साल पूरा करने के साथ ही, २५ वर्षीय विहारी भारत के टेस्ट सेट-अप यानी कि भारत के टेस्ट टीम के प्रमुख सदस्य बन गए हैं.
वीरेंद्र सहवाग ने बताई विराट-रोहित, अपने और धोनी के बीच उठी आपसी मतभेद की सच्चाई
बंगाल के २१ साल के इस गेंदबाज ने अनिल कुंबले के एक पारी में १० विकेट लेने के कारनामे को दोहराया
इंडियन प्रीमियर लीग २०१४: सर्वश्रेष्ठ गेंदबाजी
विडियो: राहुल के १५० रनों के बीच कही आप ये सीन तो मिस नहीं कर गये
सौरव गांगुली ने कोलकाता में किया क्रिकेट स्कूल का उद्घाटन | hindi |
ییتھ صفہس آو ٲخرَس پیٹھ ٧ مارچ ٢٠١٣ ١٦:٤٨ بجے اؠڑیٹ کرنہ. | kashmiri |
/*
* To change this license header, choose License Headers in Project Properties.
* To change this template file, choose Tools | Templates
* and open the template in the editor.
*/
package com.web.mavenproject6.other;
import com.taskadapter.redmineapi.IssueManager;
import com.taskadapter.redmineapi.RedmineException;
import com.taskadapter.redmineapi.RedmineManagerFactory;
import com.taskadapter.redmineapi.bean.CustomField;
import com.taskadapter.redmineapi.bean.Issue;
import com.taskadapter.redmineapi.bean.IssueCategory;
import com.taskadapter.redmineapi.bean.IssueFactory;
import com.taskadapter.redmineapi.bean.Project;
import com.taskadapter.redmineapi.bean.Tracker;
import com.taskadapter.redmineapi.bean.User;
import java.util.Date;
import java.util.List;
import org.json.JSONArray;
import org.json.JSONException;
import org.json.JSONObject;
import org.springframework.beans.factory.annotation.Autowired;
import org.springframework.core.env.Environment;
import org.springframework.stereotype.Component;
/**
*
* @author Aleks
*/
//@Component
public class RedmineManager {
@Autowired
private Environment env;
private com.taskadapter.redmineapi.RedmineManager mgr;
private IssueManager issueManager;
public RedmineManager() {
this.mgr = RedmineManagerFactory.createWithApiKey(
env.getProperty("redmine.uri"),
env.getProperty("redmine.api.accessKey")
);
this.issueManager = mgr.getIssueManager();
}
public List<Issue> getIssues(String projectKey) throws RedmineException {
return issueManager.getIssues(projectKey, null);
}
public Issue newIssue(int projectId, String subject, JSONObject j, Object... o) throws RedmineException, JSONException {
Issue is = IssueFactory.create(projectId, subject);
is.setAuthor(mgr.getUserManager().getCurrentUser());
is.setCreatedOn(new Date());
if (o != null) {
for (Object obj : o) {
if (obj instanceof User) {
is.setAssignee((User) obj);
}
if (obj instanceof IssueCategory) {
is.setCategory((IssueCategory) obj);
}
if (obj instanceof Project) {
is.setProject((Project) obj);
}
if (obj instanceof Tracker) {
is.setTracker((Tracker) obj);
}
}
}
if (j != null) {
is.setDescription(j.isNull("description") ? "" : j.getString("description"));
is.setDoneRatio(j.isNull("doneRatio") ? 0 : Integer.parseInt(j.getString("doneRatio")));
is.setStatusName(j.isNull("statusName") ? "" : j.getString("statusName"));
}
return issueManager.createIssue(is);
}
public Issue getIssue(Integer id) throws RedmineException {
return issueManager.getIssueById(id);
}
public void removerIssue(Integer id) throws RedmineException{
issueManager.deleteIssue(id);
}
public com.taskadapter.redmineapi.RedmineManager getManager(){
return mgr;
}
}
| code |
शो पर नरेंद्र मोदी को बुलाना चाहते हैं: कपिल शर्मा
अपने मशहूर टीवी शो में बॉलीवुड से लेकर खेल जगत तक की दिग्गज हस्तियों को बुला चुके कॉमेडियन कपिल शर्मा अब नेताओं को अपने शो पर मेहमान के तौर पर बुलाना चाहते हैं। इसी क्रम में उनकी एक बड़ी इच्छा प्रधानमंत्री नरेंद्र मोदी को अपने शो पर बुलाने की है क्योंकि कपिल को उनकी कहानी प्रेरणादायी लगती है।
हाल ही में कपिल ने कहा, मैं अपने नए शो में नरेंद्र मोदी को बुलाना चाहता हूं। मैं हाल ही में टीवी देख रहा था। मैंने एलेन के शो पर बराक आेबामा को देखा। यह शानदार है। हमारे यहां भी लोगों से जुडऩे वाले नेता होने चाहिए। कपिल ने कहा, यदि मोदी मेरे शो पर आते हैं तो हम राजनीति, दल आदि पर बात नहीं करेंगे। मैं जानना चाहूंगा कि एक छोटे से शहर से आने वाला एक आदमी कैसे इतना लंबा सफर तय करके हमारे देश का प्रधानमंत्री बन गया? यह एक प्रेरक कहानी है। मैं उनसे बात करने की कोशिश करूंगा।
कपिल ने कहा कि उन्हें इस बात की खुशी है कि कलर्स चैनल पर आने वाला उनका शो कॉमेडी नाइट्स विद कपिल खत्म हो गया है क्योंकि अब उन्हें कुछ नया करने का अवसर मिल रहा है। उन्होंने कहा, उस शो के खत्म होने से मुझे अच्छा लग रहा है क्योंकि उस शो में किरदार तय थे और अब हमें कुछ अलग करने का मौका मिल रहा है। हमारे इस नए शो को लेकर हर कोई उत्साहित है। हम एक अलग किस्म का शो बना रहे हैं।
हमने नहीं दिया धोखा : करिश्मा-उपेन
पुनीत वशिष्ठ ने कहा बिग बॉस के घर को अलविदा
बिग बॉस सीजन १० के दरवाजे आम जन के लिए खुलेंगे | hindi |
Perhaps you have already guessed that I like to read. Yes, I love to read and love to share my impressions of the books. You can find my profile on Goodreads.
But now let me tell you some words about books that I read in 2015. | english |
نو شکلہ تہٕ نو انمانہ | kashmiri |
\begin{equation}gin{exam}in{document}
\title{Gromov hyperbolicity, John spaces and quasihyperbolic geodesics}
\author{Qingshan Zhou}
\address{Qingshan Zhou, School of Mathematics and Big Data, Foshan University, Foshan, Guangdong 528000, People's Republic
of China} \email{q476308142@qq.com}
\author{Yaxiang Li${}^{\mathbf{*}}$}
\address{Yaxiang Li, Department of Mathematics, Hunan First Normal University, Changsha,
Hunan 410205, People's Republic
of China} \email{yaxiangli@163.com}
\author{Antti Rasila}
\address{Antti Rasila, College of Science, Guangdong Technion -- Israel Institute of Technology, Shantou, Guangdong 515063, People's Republic
of China} \email{antti.rasila@gtiit.edu.cn; antti.rasila@iki.fi}
\def\@arabic\c@footnote{}
\footnotetext{ \texttt{\tiny File:~\jobname .tex,
printed: \number\year-\number\month-\number\day,
\thehours.\ifnum\theminutes<10{0}\fi\theminutes}
} \makeatletter\def\@arabic\c@footnote{\@arabic\c@footnote}\makeatother
\date{}
\subjclass[2010]{Primary: 30C65, 30L10, 30F45; Secondary: 30C20} \keywords{ Quasihyperbolic metric, Gromov hyperbolic spaces, John spaces, quasihyperbolic geodesic.\\
${}^{\mathbf{*}}$ Corresponding author}
\begin{equation}gin{exam}in{abstract} We show that every quasihyperbolic geodesic in a John space admitting a roughly starlike Gromov hyperbolic quasihyperbolization is a cone arc. This result provides a new approach to the elementary metric geometry question, formulated in \cite[Question 2]{Hei89}, which has been studied by Gehring, Hag, Martio and Heinonen. As an application, we obtain a simple geometric condition connecting uniformity of the space with the existence of Gromov hyperbolic quasihyperbolization.
\end{abstract}
\thanks{The research was partly supported by NNSF of
China (Nos. 11601529, 11671127, 11571216).}
\maketitle{} \pagestyle{myheadings} \markboth{}{}
\section{Introduction}
The unit disk or Poincar\'e disk $\mathbb{D}$ serves as a canonical model in studying of conformal mappings and hyperbolic geometry in complex analysis. It is noncomplete metric space with the metric inherited from the two dimensional Euclidean space $\mathbb{R}^2$. On the other hand, the unit disk equipped with the Poincar\'e metric is complete Riemannian $2$-manifold with constant negative curvature. This observation can be used in investigating the hyperbolic metric on planar domains and conformal mappings between them. A generalization of this idea to higher dimensional spaces, involving quasihyperbolic metrics and Gromov hyperbolicity, was studied by Bonk, Heinonen and Koskela in \cite{BHK}.
Well-known geometric properties of a hyperbolic geodesic $[x,y]\in \mathbb{D}$ with respect to the Euclidean metric are:
\begin{equation}gin{exam}in{itemize}
\item $\ell([x,y])\leq C|x-y|$,
\item $\min\{\ell([x,z]),\ell([z,y])\}\leq C{\operatorname{dist}}(z,\partial \mathbb{D})$
\end{itemize}
for all $z\in [x,y]$, where $C$ is a universal constant. The first of the above conditions says that hyperbolic geodesic essentially minimizes the length of all curves connecting the endpoints, namely, the Gehring-Haymann condition. The second one is called the cone condition or the double twisted condition.
Martio and Sarvas studied in \cite{MS78} global injectivity properties of locally injective mappings. They considered a class of domains of $\mathbb{R}^n$, named by {\it uniform domains}, which means every pair of points can be connected by a curve satisfies the above two conditions for some constant $C\geq 1$. In \cite{GO}, Gehring and Osgood investigated the geometric properties of {\it quasihyperbolic metric}, which was introduced by Gehring and Palka \cite{GP76}, and proved that every quasihyperbolic geodesic in a Euclidean uniform domain also satisfies the above two conditions.
It should be noted that the class of domains on $\mathbb{R}^n$, which only satisfies the second condition known as {\it John domains} is large and of independent interest. For instance, the slit disk on $\mathbb{R}^2$ is an example of such domain. This class was first considered by John \cite{Jo61} in the context of elasticity theory. Many characterizations of uniform and John domains can be found in the literature and the importance of these classes of domains in function theory is well established, see for example \cite{GGKN17, LVZ17}.
From a geometric point of view, it is natural question, whether each quasihyperbolic geodesic of a John domain is a cone arc. This question was pointed out already in 1989 by Gehring, Hag and Martio \cite{GHM}:
\begin{equation}gin{ques}\leftarrowbel{q-1}
Suppose $D\subset \mathbb{R}^n$ is a $c$-John domain and that $\gamma$ is a quasihyperbolic geodesic in $D$. Is $\gamma$ a $b$-cone arc for some $b=b(c)$?
\end{ques}
They proved in \cite[Theorem $4.1$]{GHM} that quasihyperbolic geodesic in a plane simply connected John domain is a cone arc. They also constructed several examples to show that a similar result does not hold in higher dimensions. Furthermore, Heinonen has posed the following closely related problem concerning John disks:
\begin{equation}gin{ques}\leftarrowbel{q-2}$($\cite[Question 2]{Hei89}$)$
Suppose $D\subset \mathbb{R}^n$ is a $c$-John domain which is quasiconformally equivalent to the unit ball $\mathbb{B}$ and that $\gamma$ is a quasihyperbolic geodesic in $D$. Is $\gamma$ a $b$-cone arc for some constant $b$?
\end{ques}
With the help of the conformal modulus of path families and Ahlfors $n$-regularity of $n$-dimensional Hausdorff measure of $\mathbb{R}^n$, Bonk, Heinonen and Koskela \cite[Theorem $7.12$]{BHK} gave an affirmative answer to Question \ref{q-2} for bounded domains with the constant dependence of the space dimension $n$. Recently, Guo \cite[Remark 3.10]{Guo15} provided a geometric method to deal with this question. His method was based on the result that a noncomplete metric space with a roughly starlike Gromov hyperbolic quasihyperbolization satisfies the Gehring-Hayman condition and the ball separation condition. These properties were established by Koskela, Lammi and Manojlovi\'{c} in \cite[Theorem $1.2$]{KLM14}. The constant $b$ in their results depends on the dimension $n$ as well. The second author of this paper considered a related question for quasihyperbolic quasigeodesics in the setting of Banach spaces \cite{Li}. Note that quasihyperbolic geodesics may not exist in infinite-dimensional spaces, even with assumption of convexity \cite{RT2}.
The concept of uniformity in a metric space setting was first introduced by Bonk, Heinonen and Koskela \cite{BHK}, where they connected the uniformity to the negative curvature of the space that is understood in the sense of Gromov. Moreover, they generalized the result of Gehring and Osgood and showed that every quasihyperbolic geodesic in a $c$-uniform space must be a $C$-uniform arc with $C=C(c)$, see \cite[Theorem 2.10]{BHK}. They also proved that $c$-uniform space is a Gromov $\delta$-hyperbolic with respect to its quasihyperbolic metric for some constant $\delta=\delta(c)$, see \cite[Theorem 3.6]{BHK}.
In view of the above results, it is natural to consider the following more general question:
\begin{equation}gin{ques}\leftarrowbel{q-3}
Let $D$ be a locally compact, rectifiably connected noncomplete metric space. If $D$ is an $a$-John space and $(D,k)$ is $\delta$-hyperbolic, is every quasihyperbolic geodesic $\gamma$ a $b$-cone arc with $b$ depending only on $a$ and $\delta$?
\end{ques}
In this paper, we study these questions. Our main result is the following:
\begin{equation}gin{exam}in{thm}\leftarrowbel{thm-1} Let $D$ be a locally compact, rectifiably connected noncomplete metric space. If $D$ is $a$-John and $(D,k)$ is $K$-roughly starlike and $\delta$-hyperbolic, then every quasihyperbolic geodesic in $D$ is a $b$-cone arc where $b$ depends only on $a, \delta$ and $K$.
\end{thm}
Every proper domain $D$ in $\mathbb{R}^n$ is a locally compact, rectifiably connected noncomplete metric space. Following terminology of \cite{BB03}, we call a locally compact, rectifiably connected noncomplete metric space $(D,d)$ {\it minimally nice}.
For a minimally nice space $(D,d)$, we say that $D$ has a {\it Gromov hyperbolic quasihyperbolization}, if $(D,k)$ is $\delta$-hyperbolic for some constant $\delta\geq 0$, where $k$ is the quasihyperbolic metric (for definition see Subsection \ref{sub-2.2}).
\begin{equation}gin{rem}
The class of minimally nice John metric spaces, which admit a roughly starlike Gromov hyperbolic quasihyperbolization, is very wide. For example, it includes (inner) uniform domains (more generally, uniform metric spaces),
simply connected John domains in the plane, and Gromov $\delta$-hyperbolic John domains in $\mathbb{R}^n$.
\end{rem}
\begin{equation}gin{rem}
In view of the above, Theorem \ref{thm-1} states that all of the quasihyperbolic geodesics in the mentioned spaces are cone arcs. Moreover, Theorem \ref{thm-1} answers positively to question \ref{q-2} and also to question \ref{q-3} under a relatively mild condition.
\end{rem}
\begin{equation}gin{rem} The main tool in the proof of Theorem \ref{thm-1} is the uniformization process of (Gromov) hyperbolic spaces, which was introduced by Bonk, Heinonen and Koskela in \cite{BHK}. They proved that each proper, geodesic and roughly starlike $\delta$-hyperbolic space is quasihyperbolically equivalent to a $c$-uniform space; see \cite[4.5 and 4.37]{BHK}. The uniformization process of Bonk, Heinonen and Koskela has many applications and is an important tool in many related papers, see e.g. \cite{BB03, KLM14}.
\end{rem}
From \cite[Theorem 3.22]{Vai05} it follows that every $\delta$-hyperbolic domain of ${\mathbb R}^n$ is $K$-roughly starlike with $K$ depending only on $\delta$. Then we have the following corollary of Theorem \ref{thm-1}.
\begin{equation}gin{exam}in{cor} Every quasihyperbolic geodesic in an $a$-John, $\delta$-hyperbolic domain $D$ of ${\mathbb R}^n$ is a $b$-cone arc with $b$ depending only on $a$ and $\delta$. \end{cor}
\begin{equation}gin{rem} A proper domain $D$ in $\mathbb{R}^n$ is called $\delta$-{\it hyperbolic} for some $\delta\geq 0$, if $D$ has a Gromov hyperbolic quasihyperbolization. We remark that the above result is an improvement of \cite[Lemma $3.9$]{Guo15} whenever $\varphi(t)=Ct$ for some positive constant $C$. Also, we do not require the domain to be bounded.
\end{rem}
\begin{equation}gin{rem} There are many applications of the above mentioned classes of domains of $\mathbb{R}^n$ in the quasiconformal mappings and potential theory,
see e.g. \cite{BHK, CP17,GNV94,Guo15, NV}. A crucial ingredient in the related arguments is based on the fact that quasihyperbolic geodesics in Gromov hyperbolic John domains of $\mathbb{R}^n$ are inner uniform curves.
\end{rem}
As another motivation of this stude, we remark that Bonk, Heinonen and Koskela established the following characterization of Gromov hyperbolic domains on the $2$-sphere in \cite{BHK}.
\begin{equation}gin{exam}in{Thm}\leftarrowbel{Thm-1} $($\cite[Theorem 1.12]{BHK}$)$ Gromov hyperbolic domains on the $2$-sphere are precisely the conformal images of inner uniform slit domains.
\end{Thm}
A {\it slit domain} is a proper subdomain $D$ of Riemann sphere such that each component of its complement is a point or a line segment parallel to the real or imaginary axis. It is well known that every domain in Riemann sphere is conformally equivalent to a slit domain. In \cite{BHK}, Bonk, Heinonen and Koskela also pointed out that their proof of Theorem \Ref{Thm-1} is ``surprisingly indirect, using among other things the theory of modulus and Loewner spaces as developed recently in \cite{HK}, plus techniques from harmonic analysis", and ask for an elementary proof as well.
In \cite{BB03}, Balogh and Buckley proved that a minimally nice metric space has a Gromov hyperbolic quasihyperbolization if and only if it satisfies the Gehring-Hayman condition and a ball separation condition. Their proof is also based on an analytic assumption that the space supports a suitable Poincar\'{e} inequality. Recently, Koskela, Lammi and Manojlovi\'{c} in \cite{KLM14} observed that Poincar\'{e} inequalities are not critical for this characterization of Gromov hyperbolicity, see \cite[Theorem 1.2]{KLM14}.
By using the above results, and as an application of Theorem \ref{thm-1}, we give the following simple geometric condition connecting the uniformity of a space to its other properties:
\begin{equation}gin{exam}in{thm}\leftarrowbel{thm-2} Let $Q>1$ and let $(X,d,\mu)$ be a proper, $Q$-regular $A$-annularly quasiconvex length metric measure space. Let $D$ be a bounded proper subdomain of $X$. Then $D$ is uniform if and only if it is John or linearly locally connected, quasiconvex, and has a Gromov hyperbolic quasihyperbolization.
\end{thm}
\begin{equation}gin{rem} With the aid of Theorem \ref{thm-1} and some auxiliary results obtained in \cite{KLM14}, the proof of Theorem \ref{thm-2} is essentially elementary and only needs the techniques from metric geometry and some estimates concerning the quasihyperbolic metrics. It is not difficult to find that Theorem \Ref{Thm-1} is a direct corollary of Theorem \ref{thm-2}.
\end{rem}
This paper is organized as follows. Section 2 contains notation and the basic definitions and auxiliary lemmas. In Section 3, we will prove Theorem \ref{thm-1}. The proof of Theorem \ref{thm-2} is presented in Section 4.
\section{Preliminaries}
\subsection{Metric geometry} Let $(D, d)$ be a metric space, and let $B(x,r)$ and $\overline{B}(x,r)$ be the open ball and closed ball (of radius $r$ centered at the point $x$) in $D$, respectively. For a set $A$ in $D$, we use $\overline{A}$ to denote the metric completion of $A$ and $\partial A=\overline{A}\setminus A$ to be its metric boundary. A metric space $D$ is called {\it proper} if its closed balls are compact. Following terminology of \cite{BB03}, we call a locally compact, rectifiably connected noncomplete metric space $(D,d)$ {\it minimally nice}.
By a curve, we mean a continuous function $\gamma:$ $[a,b]\to D$. If $\gamma$ is an embedding of $I$,
it is also called an {\it arc}.
The image set $\gamma(I)$ of $\gamma$ is also denoted by $\gamma$. A curve $\gamma$ is called {\it rectifiably}, if the length $\ell_d(\gamma)<\infty$.
A metric space $(D, d)$ is called {\it rectifiably connected} if every pair of points in $D$ can be joined with a rectifiable
curve $\gamma$.
The length function associated with a rectifiable curve $\gamma$: $[a,b]\to D$ is $z_{\gamma}$: $[a,b]\to [0, \ell(\gamma)]$, given by
$z_{\gamma}(t)=\ell(\gamma|_{[a,t]})$.
For any rectifiable curve $\gamma:$ $[a,b]\to D$, there is a unique map $\gamma_s:$ $[0, \ell(\gamma)]\to D$ such that $\gamma=\gamma_s\circ z_{\gamma}$. Obviously,
$\ell(\gamma_s|_{[0,t]})=t$ for $t\in [0, \ell(\gamma)]$. The curve $\gamma_s$ is called the {\it arclength parametrization} of $\gamma$.
For a rectifiable curve $\gamma$ in $D$, the line integral over $\gamma$ of each Borel function $\varrho:$ $D\to [0, \infty)$ is
$$\int_{\gamma}\varrho ds=\int_{0}^{\ell(\gamma)}\varrho\circ \gamma_s(t) dt.$$
We say an arc $\gamma$ is {\it geodesic} joining $x$ and $y$ in $D$ means that $\gamma$ is a map from an interval $I$ to $D$ such that $\gamma(0)=x$, $\gamma(l)=y$ and
$$\;\;\;\;\;\;\;\;d(\gamma(t),\gamma(t'))=|t-t'|\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mbox{for all}\;\;t,t'\in I.$$
Every rectifiably connected metric space $(D, d)$ admits a natural (or intrinsic) metric, its so-called length distance given by
$$\ell(x, y) := \inf\ell(\gamma)$$ where $ \gamma$ is a rectifiable curve joining $ x, y $ in $D.$
A metric space $(D, d)$ is a {\it length space} provided that $d(x, y) = \ell(x, y)$ for all points $x, y\in D$. It is also common to call such a $d$ an intrinsic distance function.
\subsection{Quasihyperbolic metric, quasigeodesics and solid arcs}\leftarrowbel{sub-2.2}
Suppose $\gamma $ is a rectifiable curve in a minimally nice space $(D,d)$, its {\it quasihyperbolic length} is the number:
$$\ell_{k_D}(\gamma)=\int_{\gamma}\frac{|dz|}{d_D(z)},
$$ where $d_D(z)={\operatorname{dist}}(x,\partial D)$ is the distance from $z$ to the boundary of $D$.
For each pair of points $x$, $y$ in $D$, the {\it quasihyperbolic distance}
$k_D(x,y)$ between $x$ and $y$ is defined by
$$k_D(x,y)=\inf\ell_{k_D}(\gamma),
$$
where the infimum is taken over all rectifiable curves $\gamma$
joining $x$ to $y$ in $D$.
We remark that the resulting space $(D,k_D)$ is complete, proper and geodesic (cf. \cite[Proposition $2.8$]{BHK}).
We recall the following basic estimates for quasihyperbolic distance that
first used by Gehring and Palka \cite[2.1]{GP76} (see also \cite[(2.3), (2.4)]{BHK}):
\begin{equation}\leftarrowbel{li-1} k_D(x,y)\geq \log{\mathcal B}ig(1+\frac{d(x,y)}
{\min\{d_D(x), d_D(y)\}}{\mathcal B}ig)\geq \log|\frac{d_D(x)}{d_D(y)}|.\end{equation}
In fact, more generally, we have
\begin{equation}\leftarrowbel{li-2} \ell_{k_D}(\gamma)\geq \log{\mathcal B}ig(1+\frac{\ell(\gamma)}
{\min\{d_D(x), d_D(y)\}}{\mathcal B}ig)
\end{equation}
Moreover, we have the following estimate:
\begin{equation}gin{exam}in{lem}\leftarrowbel{newlemlabel}
Let $D$ be a minimally nice length space. Then for $x,y\in D$ with $d(x,y) < d_D(x)$, we have
$$k_D(x,y)\leq \frac{d(x,y)}{d_D(x)-d(x,y)}.$$
\end{lem}
\begin{equation}gin{pf} Let $0<\epsilon<\frac{1}{2}(d_D(x)-d(x,y))$. Since $D$ is a length space, there is a curve $\alpha$ joining $x$ and $y$ such that $\ell(\alpha)\leq d(x,y)+\epsilon$. Thus we have $\ell(\alpha)<d_D(x)$, which implies that $\alpha\subset B(x,d_D(x))\cap D$. Hence, we compute
$$k_D(x,y)\leq \int_{\alpha}\frac{|dz|}{d_D(z)}\leq \frac{\ell(\alpha)}{d_D(x)-\ell(\alpha)}<\frac{d(x,y)+\epsilon}{d_D(x)-d(x,y)-\epsilon}.$$
By letting $\epsilon\to 0$, we get the desired inequality.
\end{pf}
\begin{equation}gin{exam}in{defn} \leftarrowbel{def1.4}
Suppose $\gamma$ is an arc in a minimally nice space $D$. The arc may be closed, open or half open. Let $\overline{x}=(x_0,$ $\ldots,$ $x_n)$,
$n\geq 1$, be a finite sequence of successive points of $\gamma$.
For $h\geq 0$, we say that $\overline{x}$ is {\it $h$-coarse} if
$k_D(x_{j-1}, x_j)\geq h$ for all $1\leq j\leq n$. Let $\Phi_{k_D}(\gamma,h)$
denote the family of all $h$-coarse sequences of $\gamma$. Set
$$z_{k_D}(\overline{x})=\sum^{n}_{j=1}k_D(x_{j-1}, x_j)$$ and
$$\ell_{k_D}(\gamma, h)=\sup \{z_{k_D}(\overline{x}): \overline{x}\in \Phi_{k_D}(\gamma,h)\}$$
with the agreement that $\ell_{k_D}(\gamma, h)=0$ if
$\Phi_{k_D}(\gamma,h)=\emptyset$. Then the number $\ell_{k_D}(\gamma, h)$ is the
{\it $h$-coarse quasihyperbolic length} of $\gamma$. \end{defn}
\begin{equation}gin{exam}in{defn} \leftarrowbel{def1.5} Let $D$ be a minimally nice space. An arc $\gamma\subset D$
is {\it $(\nu, h)$-solid} with $\nu\geq 1$ and $h\geq 0$ if
$$\ell_{k_D}(\gamma[x,y], h)\leq \nu\;k_D(x,y)$$ for all $x$, $y\in \gamma$. \end{defn}
Let $\leftarrowmbda\geq 1$ and $\mu\geq 0$.
A curve $\gamma$ in $D$ is a {\it $(\leftarrowmbda, \mu)$-quasigeodesic} if
$$\ell_{k_D}(x,y) \leq \leftarrowmbda k_D(x,y)+\mu$$
for all $x,y\in \gamma.$ If $\leftarrowmbda=1$, $\mu=0$, then $\gamma$ is a quasihyperbolic geodesic.
\begin{equation}gin{exam}in{defn}Let $D$ and $D'$ be two minimally nice metric spaces. We say
that a homeomorphism $f: D\to D'$ is an {\it $M$-quasihyperbolic mapping},
or briefly {\it $M$-QH}, if there exists a constant $M\geq 1$ such that for all $x$, $y\in D$,
$$\frac{1 }{M}k_D(x,y)\leq k_{D'}(f(x),f(y))\leq M\;k_D(x,y) .$$\end{defn}
In the following, we use $x$, $y$, $z$, $\ldots$ to
denote the points in $D$, and $x'$, $y'$, $z'$, $\ldots$ the images
of $x$, $y$, $z$, $\ldots$ in $D'$, respectively, under $f$. For
arcs $\alpha$, $\begin{equation}ta$, $\gamma$, $\ldots$ in $D$, we also use
$\alpha'$, $\begin{equation}ta'$, $\gamma'$, $\ldots$ to denote their images in
$D'$.
Under quasihyperbolic mappings, we have the following useful relationship between $(\leftarrowmbda, \mu)$-quasigeodesics and solid arcs.
\begin{equation}gin{exam}in{lem}\leftarrowbel{ll-001} Suppose that $G$ and $G'$ are minimally nice metric spaces. If $f:\;G\to G'$ is $M$-QH, and $\gamma$ is a $(\leftarrowmbda, \mu)$-quasigeodesic in $G$, then there are constants $\nu=\nu(\leftarrowmbda, \mu, M)$ and $h=h(\leftarrowmbda, \mu, M)$ such that
the image $\gamma'$ of $\gamma$ under $f$ is $(\nu,h)$-solid in $G'$.
\end{lem}
\begin{equation}gin{pf}
Let $\gamma$ be a $(\leftarrowmbda,\mu)$-quasigeodesic and let $$h=M(\leftarrowmbda+\mu)\;\; \mbox{and}\;\; \nu=M^2(\leftarrowmbda+\mu).$$
To show that $\gamma'$ is $(\nu,h)$-solid, we only need to verify that for $x$, $y\in \gamma$,
\begin{equation}\leftarrowbel{new-eq-3}\ell_{k_{G'}}(\gamma'[x',y'],h)\leq\nu k_{G'}(x',y').\end{equation} We prove this by considering two cases.
The first case is: $k_G(x,y)<1$. Then for $z$, $w\in\gamma[x, y]$, we have
$$k_{G'}(z',w')\leq Mk_G(z,w)\leq M(\leftarrowmbda k_G(x,y)+\mu)<M(\leftarrowmbda+\mu)=h,$$
and so
\begin{equation}\leftarrowbel{ma-3}\ell_{k_{G'}}(\gamma'[x',y'],h)=0.\end{equation}
Now, we consider the other case: $k_G(x,y)\geq 1$. Then with the aid of \cite[Theorem 4.9]{Vai6}, we have
\begin{equation}gin{eqnarray}\leftarrowbel{ma-4}
\ell_{k_{G'}}(\gamma'[x',y'],h) &\leq&
M\ell_{k_G}(\gamma[x,y])\leq M(\leftarrowmbda k_G(x,y)+\mu)\\ \nonumber &\leq& M(\leftarrowmbda+\mu)k_{G}(x,y) \leq M^2(\leftarrowmbda+\mu)k_{G'}(x',y').\end{eqnarray}
It follows from \eqref{ma-3} and \eqref{ma-4} that \eqref{new-eq-3} holds, completing the proof.\end{pf}
\subsection{Uniform spaces and John spaces}
In this subsection we first recall the definitions of John spaces, cone arcs and uniform spaces. We also give some results related to some special arcs which will be useful later in the proof of the main result.
\begin{equation}gin{exam}in{defn} Let $a\geq 1$. A minimally nice space $(D,d)$ is called {\it $a$-John} if each pair of points $x,y\in D$ can be joined by a rectifiable arc $\alpha$ in $D$ such that for all $z\in \alpha$
$$\min\{\ell(\alpha[x,z]), \ell(\alpha[z,y])\}\leq a d_D(z),$$
where $\alpha[x,z]$ and $\alpha[z,y]$ denote two subarcs of $\alpha$ divided by the point $z$. The arc $\alpha$ is called an {\it $a$-cone} arc.
\end{defn}
\begin{equation}gin{exam}in{defn} Let $c\geq 1$. A minimally nice space $(D,d)$ is called {\it $c$-uniform} if each pair of points $x,y\in D$ can be joined by a $c$-uniform arc. An arc $\alpha$ is called {\it $c$-uniform} if it is a $c$-cone arc and satisfies the $c$-quasiconvexity, that is, $\ell(\alpha)\leq c d(x,y).$
\end{defn}
\begin{equation}gin{exam}in{Lem}\leftarrowbel{Lem-uniform}$($\cite[(2.16)]{BHK}$)$\; If $D$ is a $c$-uniform metric space, then for all $x,y\in D$, we have
$$ k_{D}(x,y)\leq 4c^2 \log{\mathcal B}ig(1+\frac{d(x,y)}{\min\{d_{D}(x),d_{D}(y)\}}{\mathcal B}ig).$$\end{Lem}
The following properties of solid arcs in uniform metric spaces is from \cite{LVZ2} which will be used in our proofs.
\begin{equation}gin{exam}in{Lem}\leftarrowbel{Lem13''}$($\cite[Lemma 3]{LVZ2}$)$\, Suppose that $D$ is a $c$-uniform space, and that $\gamma$ is a $(\nu,h)$-solid arc in $D$ with endpoints $x$, $y$. Let $d_D(x_0)=\max_{p\in \gamma}d_D(p)$. Then there exist constants
$a_1=a_1( c, \nu, h)\geq 1$ and $a_2=a_2(c, \nu, h)\geq 1$ such that
\begin{equation}gin{exam}in{enumerate} \item
${\operatorname{diam}}(\gamma[x,u])\leq a_1 d_D(u)$ for $u\in \gamma[x,x_0],$ and ${\operatorname{diam}}(\gamma[y,v])\leq a_1 d_D(v)$ for $v\in \gamma[y, x_0]$;
\item ${\operatorname{diam}}(\gamma)\leq \max\big\{a_2 d(x,y), 2(e^h-1)\min\{d_D(x),d_D(y)\}\big\}.$
\end{enumerate}
\end{Lem}
Next we discuss the properties of cone arcs.
\begin{equation}gin{exam}in{lem}\leftarrowbel{eq-8} Let $\alpha[x,y]$ be an $a$-cone arc in $D$ and let $z_0$ bisect the arclength of
$\alpha[x,y]$. Then for each $z_1$, $z_2\in\alpha[x,z_0]$ $($or
$\alpha[y,z_0]$$)$ with $z_2\in \alpha[z_1,z_0]$, we have $$k_D(z_1,z_2)\leq \ell_k(\alpha[z_1,z_2])\leq 2a \log\big(1+\frac{2\ell(\alpha[z_1,z_2])}{d_D(z_1)}\big)$$ and $$\ell_{k}(\alpha[z_1,z_2])\leq
4a^2k_{D}(z_1,z_2)+4a^2.$$
\end{lem}
\begin{equation}gin{pf} By symmetry, we only need to verify the assertion in the case $z_1$, $z_2\in\alpha[x,z_0]$. To this end, for $z_2\in \alpha[z_1,z_0]$ be given, we have
$$d_D(z_2)\geq \frac{1}{a}\ell(\alpha[z_1,z_2]).$$
If $z_2\subset
B(z_1, \frac{1}{2}d_D(z_1))$, thus one finds that $d_D(z_2)\geq
\frac{1}{2}d_D(z_1)$.
Otherwise, we have
$d_D(z_2)\geq\frac{1}{2a}d_D(z_1)$. Hence in both cases we obtain
$$d_D(z_2)\geq \frac{1}{4a}[2\ell(\alpha[z_1,z_2])+d_D(z_1)],$$
which yields that
\begin{equation}gin{exam}in{eqnarray*}k_{D}(z_1,z_2) &\leq& \ell_k(\alpha[z_1,z_2])= \int_{\alpha[z_1,z_2]}\frac{|dz|}{d_D(z)}\\ \nonumber
&\leq& 2a\log{\mathcal B}ig(1+\frac{2\ell(\alpha[z_1,z_2])}{d_D(z_1)}{\mathcal B}ig)\\ \nonumber
&\leq& 4a^2\log{\mathcal B}ig(1+\frac{d_D(z_2)}{d_D(z_1)}{\mathcal B}ig)\\ \nonumber &\leq&
4a^2k_{D}(z_1,z_2)+4a^2,\end{eqnarray*}
as desired.
\end{pf}
\begin{equation}gin{exam}in{lem} \leftarrowbel{lem13-0-0}Suppose that
$f: D\to D'$ is an $M$-QH from an $a$-John minimally nice space $D$ to a $c$-uniform space $D'$. Let $\alpha$ be an $a$-cone arc in $D$ with end points $x$ and $y$, $z_0$ bisect the arclength of
$\alpha$, and let $d_{D'}(v'_1)=\max\{d_{D'}(u'): u'\in\alpha'[x',z'_0]\}$ and
$d_{D'}(v'_2)=\max\{d_{D'}(u'): u'\in\alpha'[y',z'_0]\}$. Then there is a constant $a_3=a_3(a,c,M)$ such that
\begin{equation}gin{exam}in{enumerate}
\item for each $z'\in \alpha'[x', v'_1]$,
$d' (x',z')\leq a_3\;d_{D'}(z')$
and for each $z'\in \alpha'[v'_1, z'_0]$, $d' (z'_0,z')\leq a_3\;d_{D'}(z')$.
\item for each $z'\in \alpha'[y', v'_2]$,
$d' (y',z')\leq a_3\;d_{D'}(z')$
and for each $z'\in \alpha'[v'_2, z'_0]$, $d' (z'_0,z')\leq a_3\;d_{D'}(z')$. \end{enumerate}
\end{lem}
\begin{equation}gin{pf} First, in the light of Lemma \ref{eq-8}, we see that $\alpha[x,z_0]$ and $\alpha[z_0,y]$ are $(4a^2,4a^2)$-quasigeodesics. Since $f: D\to D'$ is $M$-QH, we thus know from Lemma \ref{ll-001} that $\alpha'[x',z'_0]$ and $\alpha'[z'_0,y']$ are solid arcs. Moreover, by the choices of $v_1'$ and $v_2'$, $(1)$ and $(2)$ follows from Lemma \Ref{Lem13''}.
\end{pf}
\subsection{Uniformization theory of Bonk, Heinonen and Koskela }
Let $(X,d)$ be a geodesic metric space and let $\delta\geq 0$. If for all triples of geodesics $[x,y], [y,z], [z,x]$ in $(X,d)$ satisfies: every point in $[x,y]$ is within distance $\delta$ from $[y,z]\cup [z,x]$, then the space $(X,d)$ is called a {\it $\delta$-hyperbolic space}. For simplicity, in the rest of this paper when we say that a minimally nice space $X$ is {\it Gromov
hyperbolic} we mean that the space is $\delta$-hyperbolic with respect to the quasihyperbolic metric for some nonnegative constant $\delta$.
In \cite{BHK}, Bonk, Heinonen and Koskela introduced the concept of rough starlikeness of a Gromov hyperbolic space with respect to a given base point. Let $X$ be a proper, geodesic $\delta$-hyperbolic space, and let $w\in X$, we say that $X$ is {\it $K$-roughly starlike} with respect to $w$ if for each $x\in X$ there is some point $\xi\in\partial^* X$ and a geodesic ray $\gamma=[w,\xi]$ with ${\operatorname{dist}}(x,\gamma)\leq K$.
They also proved that both bounded uniform spaces and every hyperbolic domain $($a domain equipped with its quasi-hyperbolic metric is a Gromov hyperbolic space$)$ in ${\mathbb R}^n$ are roughly starlike. It turns out that this property serves as an important tool in several research, for instance \cite{BB03}, \cite{ZR} and \cite{KLM14}.
Next we recall the conformal deformations which were introduced by Bonk, Heinonen and Koskela (cf. \cite[Chapter $4$]{BHK}). Let $(X,d)$ be a minimally nice space and $w\in X$. Consider the family of conformal deformations of $(X,k)$ by the densities
$$\rho_\epsilon(x)=e^{-\epsilon k(x,w)}\;\;(\epsilon>0).$$
For $u$, $v\in X$, let
$$d_\epsilon(u,v)=\inf\int_{\gamma} \rho_\epsilon ds_k,$$
where $ds_k$ is the arc-length element with respect to the metric $k$ and the infimum is taken over all rectifiable curves $\gamma$ in $X$ with endpoints $u$ and $v$.
Then $d_\epsilon$ are metrics on $X$, and we denote the resulting metric spaces
by $X_\epsilon=(X,d_\epsilon)$.
The next result shows that the deformations $X_{\epsilon}$ are uniform spaces and each proper, geodesic and roughly starlike $\delta$-hyperbolic space is {\it quasihyperbolically equivalent} to a $c$-uniform space; see \cite[Propositions 4.5 and 4.37]{BHK}.
\begin{equation}gin{exam}in{Lem}\leftarrowbel{lem-1}$($\cite[Propositions $4.5$ and $4.37$]{BHK} or \cite[Lemma $4.12$]{BB03}$)$
Suppose $(X,d)$ is minimally nice, locally compact and that $(X,k)$ is both $\delta$-Gromov hyperbolic and $K$-roughly starlike, for some $\delta\geq 0$, $K>0$. Then $X_\epsilon$ has diameter at most $2/\epsilon$ and there are positive numbers $c, \epsilon_0$ depending only on $\delta, K$ such that $X_\epsilon$ is $c$-uniform for all $0<\epsilon\leq \epsilon_0$. Furthermore, there exists $c_0=c_0(\delta,K)\in(0,1)$ such that the quasihyperbolic metrics $k$ and $k_\epsilon$ satisfy the quasi-isometric condition
$$c_0\epsilon k(x,y)\leq k_\epsilon(x,y)\leq e \epsilon k(x,y).$$
\end{Lem}
\section{The proof of Theorem \ref{thm-1}}
Let $(D,d)$ be a minimally nice $a$-John metric space and $(D,k)$ $K$-roughly starlike, $\delta$-hyperbolic where $k$ is the quasihyperbolic metric of $D$. Then by Lemma \Ref{lem-1}, we know that there is a positive number $\epsilon=\epsilon(\delta)$ such that $(D,d_{\epsilon})$ is a $c$-uniform metric space and the identity map from $(D,d)$ to $(D,d_{\epsilon})$ is $M$-QH, where $c$ and $M$ depend only on $\delta$ and $K$. For simplicity, we denote $D=(D,d)$, $(D',d')=(D,d_{\epsilon})$ and $f$ the identity map from $D$ to $D'$.
We may assume without loss of generality that $D$ is a length space, because the length of an arc and the quasihyperbolic metrics associated to the original metric and the length metric coincide.
Fix $z_1$, $z_2\in D$ and let $\gamma$ be a quasihyperbolic geodesic joining
$z_1$, $z_2$ in $D$. Let $b=4a_4e^{a_4}$, $a_4=a_5^{8c^2M}$,
$a_5=a_6^{4a^2M}$ and $a_6=(8a_1^2a_3)^{16c^2M}a^2$, where $a_1$ and $a_3$ are the constants from Lemmas \Ref{Lem13''} and \ref{lem13-0-0}, respectively. In the following, we shall prove that $\gamma$ is a
$b$-cone arc, that is, for each $y\in\gamma$,
$$\min\{\ell(\gamma[z_1, y]),\; \ell(\gamma[z_2,
y])\}\leq b\,d_D(y).$$
Let $x_0\in \gamma$ be a point such that
$d_D(x_0)=\max\limits_{z\in \gamma}d_D(z).
$
By symmetry, we only need to prove that for $y\in\gamma[z_1,x_0]$, \begin{equation}gin{eqnarray} \leftarrowbel{John}\ell(\gamma[z_1, y])\leq b\,d_D(y).\end{eqnarray}
To this end, let $m \geq 0$
be an integer such that
$$2^{m}\, d_D(z_1)
\leq d_D(x_0)< 2^{m+1}\, d_D(z_1).
$$
And let $y_0$ be the first point in $\gamma[z_1,x_0]$ from $z_1$ to
$x_0$ with
$$d_D(y_0)=2^{m}\, d_D(z_1).
$$
Observe that if $d_D(x_0)=d_D(z_1)$, then $y_0=z_1=x_0$.
Let $y_1=z_1$. If $z_1=y_0$, we let $y_2=x_0$. It is possible that
$y_2=y_1$. If $z_1\not= y_0$, then we let $y_2,\ldots ,y_{m+1}$ be
the points such that for each $i\in \{2,\ldots,m+1\}$, $y_i$
denotes the first point in $\gamma[z_1,x_0]$ from $y_1$ to $x_0$
satisfying
$$d_D(y_i)=2^{i-1}\, d_D(y_1).$$
Then $y_{m+1}=y_0$. We let $y_{m+2}=x_0$. It is possible that
$y_{m+2}=y_{m+1}=x_0=y_0$. This possibility occurs once
$x_0=y_0$.
From the choice of $y_i$ we observe that for $y\in \gamma[y_i,y_{i+1}]$ $(i\in\{1, 2, \ldots, m+1\})$, \begin{equation}\leftarrowbel{li-newadd-1} d_D(y)<d_D(y_{i+1})=2d_D(y_i)\end{equation}
and so for all $i\in\{1, 2, \ldots, m+1\}$,
\begin{equation}\leftarrowbel{li-newadd-2} k_{D}(y_i,y_{i+1}) =\ell_k(\gamma[y_i,y_{i+1}])\geq \frac{\ell(\gamma[y_i,y_{i+1}])}{2d_D(y_i)}.\end{equation}
To prove Theorem \ref{thm-1}, we shall estimate upper bound of the quasihyperbolic distance between $y_i$ and $y_{i+1}$, which state as follows.
\begin{equation}gin{exam}in{lem}\leftarrowbel{eq-0}For each $i\in \{1,\ldots, m+1\}$, $k_{D}(y_i,y_{i+1})\leq a_4$.\end{lem}
We note that Theorem \ref{thm-1} can be obtained from Lemma \ref{eq-0} as follows.
First, we observe from \eqref{li-newadd-2} and Lemma \ref{eq-0} that for all $i\in\{1,\ldots, m+1\}$,
\begin{equation}\leftarrowbel{li-1'} \ell(\gamma[y_i,y_{i+1}])\leq
2a_4 \,d_D(y_i).\end{equation}
Further, for each $y\in \gamma[y_1,x_{0}]$, there is some $i\in
\{1,\ldots,m+1\}$ such that $y\in \gamma[y_i,y_{i+1}]$. It follows from \eqref{li-1} that
$$ \log \frac{d_D(y_i)}{d_D(y)}\leq k_D(y,y_i)\leq
\, k_D(y_i,y_{i+1})\leq a_4 ,$$ whence
$$d_D(y_i)\leq e^{ a_4 }d_D(y).$$
From which and (\ref{li-1'}) it follows that
\begin{equation}gin{eqnarray}\leftarrowbel{eq(li-3)} \ell(\gamma[z_1,y])&=&
\ell(\gamma[y_1,y_2])+\ell(\gamma[y_2,y_3])+\ldots+\ell(\gamma[y_i,y])
\\
\nonumber &\leq& 2a_4 (d_D(y_1)+d_D(y_2)+\ldots+d_D(y_i))\\ \nonumber
&\leq& 4a_4 \,d_D(y_i)\leq 4a_4 e^{a_4 }\,d_D(y),\end{eqnarray} as desired. This proves \eqref{John} and so Theorem \ref{thm-1} follows.
Hence to complete the proof of Theorem \ref{thm-1}, we only need to prove Lemma \ref{eq-0}.
\subsection{The proof of Lemma \ref{eq-0}}
Without loss of generality, we may assume that
$d_{D'}(y'_i)\leq d_{D'}(y'_{i+1})$. We note that if $ d (y_i, y_{i+1})<\frac{1}{2}d_D(y_i),$ then by Lemma \ref{newlemlabel} we have
$$k_D(y_i, y_{i+1})\leq 1,$$
as desired. Therefore, we assume in the following that
\begin{equation}gin{eqnarray}\leftarrowbel{eq(4-2)}d (y_i, y_{i+1})\geq \frac{1}{2}d_D(y_i).\end{eqnarray}
Let $\alpha_i$ be an
$a$-cone arc joining $y_i$ and $y_{i+1}$ in $D$ and let $v_i$ bisect the arclength of
$\alpha_i$. Then Lemma \ref{eq-8} implies that
\begin{equation}gin{eqnarray}\leftarrowbel{hl-eq(4-1-2)}\;\;\;\;\;k_{D}(y_i,y_{i+1})&\leq&
k_{D}(y_i,v_i)+k_{D}(v_i,y_{i+1})\\ \nonumber &\leq& 2a\bigg(\log {\mathcal B}ig( 1+\frac{2\ell(\alpha_i[y_i,v_i])}
{d_D(y_i)}{\mathcal B}ig)+\log
{\mathcal B}ig( 1+\frac{2\ell(\alpha_i[y_{i+1},v_i])} {d_D(y_{i+1})}{\mathcal B}ig)\bigg)\\ \nonumber &\leq& 4a\log {\mathcal B}ig(
1+\frac{\ell(\alpha_i)} {d_D(y_i)}{\mathcal B}ig). \nonumber
\end{eqnarray}
Now we divide the proof of Lemma \ref{eq-0} into two cases.
\begin{equation}gin{ca} \leftarrowbel{ca1} $\ell(\alpha_i)< a_5 d (y_i, y_{i+1}).$\end{ca}
Then by \eqref{li-newadd-2} and \eqref{hl-eq(4-1-2)} we compute
\begin{equation}gin{eqnarray}\leftarrowbel{eq(h-h-4-2')}
\frac{d(y_i,y_{i+1})}{2d_D(y_i)}&\leq& k_{D}(y_i,y_{i+1})
\leq 4a \log {\mathcal B}ig( 1+\frac{\ell(\alpha_i)} {d_D(y_i)}{\mathcal B}ig) \\ \nonumber
&\leq& 4a \log {\mathcal B}ig( 1+\frac{ a_5d(y_i,y_{i+1})} {d_D(y_i)}{\mathcal B}ig).\end{eqnarray} A necessary condition for \eqref{eq(h-h-4-2')} is
$$ d (y_i,y_{i+1})\leq a_5^2\,d_D(y_i).$$
Hence we deduce from (\ref{eq(h-h-4-2')}) that $k_{D}(y_i,y_{i+1})\leq
a_4$, as desired.
\begin{equation}gin{ca} \leftarrowbel{ca2} $\ell(\alpha_i)\geq a_5 d (y_i, y_{i+1}).$\end{ca}
We prove in this case by contradiction. Suppose on the contrary that
\begin{equation}gin{eqnarray}\leftarrowbel{eq(h-4-2)}k_{D}(y_i,y_{i+1})> a_4.\end{eqnarray}
Then by Lemma \Ref{Lem-uniform}, we get
\begin{equation}gin{exam}in{eqnarray*}a_4<k_{D}(y_i,y_{i+1})\leq M k_{D'}(y'_i,y'_{i+1})
\leq 4c^2M\log{\mathcal B}ig(1+\frac{d' (y'_i,y'_{i+1})}{d_{D'}(y'_i)}{\mathcal B}ig),\end{eqnarray*}
and so
\begin{equation}gin{eqnarray}\leftarrowbel{eq(h-4-1')}d' (y'_i,y'_{i+1})\geq a_5d_{D'}(y'_i).\end{eqnarray}
Therefore, by the choice of $v_i\in\alpha_i$ we obtain
$$d_D(v_i)\geq \frac{\ell(\alpha_i)}{2a}\geq \frac{a_5}{2a} d (y_i,y_{i+1})>a_6\, d (y_i,y_{i+1}),$$
we deduce from which and \eqref{eq(4-2)} that there exists a point
$v_{i,0}\in \alpha_i[y_i,v_i]$ such that
\begin{equation}\leftarrowbel{eq-11} d_D(v_{i,0})=a_6\, d (y_i,y_{i+1}).\end{equation}
Moreover, we claim that
\begin{equation}\leftarrowbel{claim1}k_{D}(y_i,v_{i,0})\leq \frac{1}{a_5}k_{D}(y_i,y_{i+1}).\end{equation}
Otherwise, we would see from Lemma \ref{eq-8} and \eqref{eq-11} that
\begin{equation}gin{exam}in{eqnarray*}k_{D}(y_i,y_{i+1})&<& a_5 k_{D}(y_i,v_{i,0})\leq 4aa_5 \log{\mathcal B}ig(1+\frac{\ell(\alpha_i[y_{i},v_{i,0}])}{d_D(y_i)}{\mathcal B}ig)
\\ \nonumber
&\leq& 4aa_5 \log{\mathcal B}ig(1+\frac{ad(v_{i,0})}{d_D(y_i)}{\mathcal B}ig)
\leq
4a^2a_5a_6\log{\mathcal B}ig(1+\frac{ d (y_i,y_{i+1})}{d_D(y_i)}{\mathcal B}ig),
\end{eqnarray*} which together with \eqref{li-newadd-2} show that $$\frac{d(y_i,y_{i+1})}{d_D(y_i)}\leq 8a^2a_5a_6\log{\mathcal B}ig(1+\frac{ d (y_i,y_{i+1})}{d_D(y_i)}{\mathcal B}ig).$$
A necessary condition for the above inequality is $$ d (y_i,y_{i+1})\leq a_5^2\,d_D(y_i).$$
This shows that $k_{D}(y_i,y_{i+1})\leq
a_4$, which contradicts $\eqref{eq(h-4-2)}$. Thus we get (\ref{claim1}).
Then it follows from Lemma \Ref{Lem-uniform}, and \eqref{claim1} that
\begin{equation}gin{exam}in{eqnarray*} k_{D'}(y'_i,v'_{i,0})&<& Mk_{D}(y_i,v_{i,0})
\leq\frac{M}{a_5}k_{D}(y_i,y_{i+1}) \\ &\leq& \frac{M^2}{ a_5}k_{D'}(y'_i,y'_{i+1})
\leq \frac{4c^2M^2}{ a_5}\log{\mathcal B}ig(1+\frac{d' (y'_i,y'_{i+1})}{d_{D'}(y'_i)}{\mathcal B}ig).
\end{eqnarray*}
Hence, by using an elementary compute we see from \eqref{li-1} and \eqref{eq(h-4-1')} that \begin{equation}gin{exam}in{eqnarray*}
\log {\mathcal B}ig(1+\frac{d' (y'_i,v'_{i,0})}{d_{D'}(y'_i)}{\mathcal B}ig) \leq k_{D'}(y'_i,v'_{i,0})\leq \log{\mathcal B}ig(1+\frac{d' (y'_i,y'_{i+1})}{a_5d_{D'}(y'_i)}{\mathcal B}ig),
\end{eqnarray*}
which implies that
\begin{equation}gin{eqnarray}\leftarrowbel{eq(hl-41-5)}d' (y'_i,v'_{i,0})<
\frac{1}{a_5}d' (y'_i,y'_{i+1}).\end{eqnarray}
Moreover, we deduce from (\ref{eq(hl-41-5)}) and
(\ref{eq(h-4-1')}) that
\begin{equation}gin{eqnarray}\leftarrowbel{eq--2} d_{D'}(v'_{i,0})\leq
d' (y'_i,v'_{i,0})+d_{D'}(y'_i)\leq
\frac{2}{a_5}d' (y'_i,y'_{i+1}).\end{eqnarray}
We recall that $v_i$ is the point in the cone arc $\alpha_i[y_i,y_{i+1}]$ which bisect the arclength of $\alpha_i$. Next we need to estimate the location of the image point $v'_i$ in $\alpha'_i$. We claim that
\begin{equation}gin{exam}in{cl}\leftarrowbel{eq--6}
$d'(y'_i,v'_i)<\frac{1}{2}d' (y'_i,y'_{i+1}).$ \end{cl}
We prove this claim by a method of contradiction. Suppose on the contrary that \begin{equation}\leftarrowbel{neweqlabel}d' (y'_i,v'_i)\geq
\frac{1}{2}d' (y'_i,y'_{i+1}).\end{equation} Let $u'_{0,i}\in\gamma'[y'_{i},
y'_{i+1}]$ be a point satisfying $$d_{D'}(u'_{0,i})=\max\{d_{D'}(w'):w'\in\gamma'[y'_{i},
y'_{i+1}]\}.$$
Then we see from Lemma \Ref{Lem13''}
that
\begin{equation}\leftarrowbel{e---1} d_{D'}(u'_{0,i})\geq \frac{1}{a_1}\max\{d' (y'_{i+1},u'_{0,i}),
d' (u'_{0,i},y'_i)\} \geq
\frac{d' (y'_i,y'_{i+1})}{2a_1}.\end{equation} This together with (\ref{eq(h-4-1')}) shows that there exists some point
$y'_{0,i}\in \gamma'[y'_i,u'_{0,i}]$ satisfying
\begin{equation}gin{eqnarray}\leftarrowbel{eq(W-l-6-1)}d_{D'}(y'_{0,i})=\frac{d' (y'_i,y'_{i+1})}{2a_1}.
\end{eqnarray}
It follows from Lemma \Ref{Lem13''} that\begin{equation}gin{eqnarray}\leftarrowbel{eq(W-l-6-1add)}d' (y'_i,y'_{0,i})\leq
a_1\,d_{D'}(y'_{0,i}).\end{eqnarray}
Let $v'_0\in\alpha'_i[y'_{i}, v'_{i}]$ satisfy $d_{D'}(v'_0)=\max\{d_{D'}(u'):u'\in\alpha'_i[y'_{i}, v'_{i}]\}$, see Figure \ref{fig01}. Then we see from Lemma
\ref{lem13-0-0} that for each $z'\in \alpha'_i[ v'_i, v'_0]$, \begin{equation}gin{eqnarray}\leftarrowbel{cla-3}d' (v'_i,z')\leq a_3 d_{D'}(z').\end{eqnarray} On the other hand, we recall that $v'_{i,0}$ is the point such that $v_{i,0}\in \alpha_i[y_i,v_i]$ and satisfying \eqref{eq-11} and \eqref{eq(hl-41-5)}. Then by \eqref{eq(hl-41-5)} and \eqref{eq--2} we have
\begin{equation}gin{exam}in{eqnarray*}d' (v'_i,v'_{i,0})&\geq&
d' (v'_i,y'_i)-d' (v'_{i,0},y'_i)\geq (\frac{1}{2}-\frac{1}{a_5})d' (y'_i,y'_{i+1})>a_3 d_{D'}(v'_{i,0}).
\end{eqnarray*}
That means $v'_0\in \alpha'_i[ v'_{i,0}, v'_i]$.
Moreover, we know from Lemma
\ref{lem13-0-0} and \eqref{neweqlabel} that $$d_{D'}(v'_0)\geq \frac{1}{a_3}\max\{d' (v'_{i},v'_0),
d' (v'_0,y'_i)\}\geq \frac{d' (y'_i,v_i')}{2a_3}\geq
\frac{d' (y'_i,y'_{i+1})}{4a_3}.$$
Hence, it follows from (\ref{eq--2}) that there exists some point $u'_0\in
\alpha'_i[v'_{i,0},v'_{0}]$ such that \begin{equation}gin{eqnarray}\leftarrowbel{eq(W-l-6-2)}
d_{D'}(u'_0)=\frac{d' (y'_i,y'_{i+1})}{4a_3},\end{eqnarray} and so Lemma \ref{lem13-0-0} leads to
$$d' (y'_i,u'_0)\leq a_3\,d_{D'}(u'_0).$$
This together with \eqref{eq(W-l-6-1)}, \eqref{eq(W-l-6-1add)} and \eqref{eq(W-l-6-2)} show that
$$d' (u'_0,y'_{0,i})\leq d' (u'_0,y'_i)+d' (y'_i,y'_{0,i})\leq 3a_3d_{D'}(u'_0).$$
Now we are ready to finish the proof of Claim \ref{eq--6}. It follows from \eqref{li-1} and Lemma \Ref{Lem-uniform} that
\begin{equation}gin{exam}in{eqnarray*}
\log \frac{d_D(u_0)}{d_D(y_{0,i})}&\leq& k_{D}(y_{0,i},u_0)
\leq M k_{D'}(y'_{0,i},u'_0) \\ \nonumber
&\leq& 4c^2M\log{\mathcal B}ig(1+\frac{d' (u'_0,y'_{0,i})}{\min\{d_{D'}(u'_0),
d_{D'}(y'_{0,i})\}}{\mathcal B}ig)\\ \nonumber &<&4c^2M\log (1+3a_3),
\end{eqnarray*}
which yields that
\begin{equation}gin{eqnarray}\leftarrowbel{eq(W-l-6-4)}d_D(u_0)\leq (1+3a_3)^{4c^2M}d_D(y_{0,i})<a_6d_D(y_{0,i}).\end{eqnarray}
On the other hand, by Lemma \ref{eq-8} we can get
\begin{equation}gin{exam}in{eqnarray*}
k_{D}(v_{i,0},u_0)\geq 4{a}^2\log{\mathcal B}ig(1+\frac{d_D(u_0)}{d_D(v_{i,0})}{\mathcal B}ig)\end{eqnarray*}
and by \eqref{li-1}, \eqref{eq--2} and \eqref{eq(W-l-6-2)} we have
that
\begin{equation}gin{exam}in{eqnarray*} k_{D}(v_{i,0},u_0) \geq k_{D'}(v'_{i,0},u'_0)
\geq\log\frac{d_{D'}(u'_0)}{d_{D'}(v'_{i,0})}
\geq\log\frac{a_5}{8a_3},\end{eqnarray*} which yields $$d_D(u_0)\geq
a_6d_D(v_{i,0}).$$ Therefore, we infer from \eqref{eq(4-2)} and
\eqref{eq-11} that
\begin{equation}gin{exam}in{align*} d_D(u_0)\geq a_6d_D(v_{i,0})=a_6^2 d (y_i, y_{i+1})
\geq \frac{ a_6^2}{4}d_D(y_{i+1})\geq \frac{
a_6^2}{4}d_D(y_{0,i}),\end{align*} which contradicts
(\ref{eq(W-l-6-4)}). Hence Claim \ref{eq--6} holds.
Now we continue the proof of Lemma \ref{eq-0}.
We first see from Claim \ref{eq--6} that
$$d' (y'_{i+1},v'_i)\geq d'(y'_i,y'_{i+1})-d' (y'_i,v'_i)>
\frac{d' (y'_i,y'_{i+1})}{2}\geq d' (y'_i,v'_i).$$ Let $q'_0\in
\alpha'_i[y'_i,v'_i]$ and $u'_1\in\alpha'_i[y'_{i+1},v'_i]$ be points such that
\begin{equation}gin{eqnarray}\leftarrowbel{112}\;\;\;\;\frac{d' (y'_i,v'_i)}{2a_3}= d' (q'_0,v_i')\,\,\;{\rm and}\,\,\; \frac{d'(y'_i,v'_i)}{2a_3}= d' (u'_1,v_i').\end{eqnarray}
Then \begin{equation}gin{exam}in{align*} d'(y'_i,q_0')\geq d'(y'_i,v_i')-d'(q'_0,v_i')=(2a_3-1)d'(q'_0,v_i')>d'(q'_0,v_i')\end{align*}
and \begin{equation}gin{exam}in{align*} d'(y'_{i+1},u_1')>d'(u'_1,v_i').\end{align*}
Thus we get from Lemma \ref{lem13-0-0} that
\begin{equation}gin{eqnarray}\leftarrowbel{eq(W-l-6'-0)}\;\;\;\;\;\;\;\;\;\;\;\; d_{D'}(q'_0)\geq \frac{d' (q'_0,v_i')}{a_3}\geq
\frac{d' (y'_i,v'_i)}{2a^2_3} \,\; \mbox{and}\;\,
d_{D'}(u'_1)\geq\frac{d' (u'_1,v_i')}{a_3}\geq
\frac{d' (y'_i,v'_i)}{2a_3^2}.\end{eqnarray}
Then it follows from Lemma \Ref{Lem-uniform}, \eqref{li-1}, \eqref{112} and \eqref{eq(W-l-6'-0)} that
\begin{equation}gin{eqnarray} \leftarrowbel{eq--7}
{\mathcal B}ig|\log\frac{d_D(u_1)}{d_D(q_0)}{\mathcal B}ig| &\leq&k_{D}(u_1,q_0) \leq M k_{D'}(u'_1, q'_0)
\\\nonumber &\leq& 4c^2M\log{\mathcal B}ig(1+\frac{d' (u'_1,q'_0)}{\min\{d_{D'}(q'_0), d_{D'}(u'_1)\}}{\mathcal B}ig)
\\\nonumber &\leq& 4c^2M\log{\mathcal B}ig(1+\frac{d' (u'_1,v'_i)+d' (v'_i,q'_0)}{\min\{d_{D'}(q'_0), d_{D'}(u'_1)\}}{\mathcal B}ig)
\\\nonumber &\leq& 4c^2M\log (1+2a_3 ),
\end{eqnarray}
which implies that
\begin{equation}gin{eqnarray}\leftarrowbel{eq(W-l-6'-2)}\frac{d_D(u_1)}{(1+2a_3 )^{4c^2M}}\leq
d_D(q_0)\leq (1+2a_3 )^{4c^2M}e^Cd_D(u_1).\end{eqnarray}
On the other hand, by \eqref{eq(h-4-1')}, \eqref{e---1} and Claim \ref{eq--6} we have
$$d' (u'_{0,i},y'_i)\geq d_{D'}(u'_{0,i})-d_{D'}(y'_i)\geq (\frac{1}{2a_1}-\frac{1}{a_5})d' (y'_{i+1},y'_i)>\frac{1}{2a_1}d' (y'_{i},v'_i).$$
Then there exists $p'_0\in
\gamma'[y'_i,u'_{0,i}]$ such that
\begin{equation}gin{eqnarray}\leftarrowbel{132}d' ( y'_i,p'_0)=\frac{d' (y'_i,v'_i)}{2a_1},\end{eqnarray}
see Figure \ref{fig02}.
This combined with \eqref{112} and Lemma \Ref{Lem13''} shows that $$d' (p'_0,q'_0)\leq d' ( p'_0,y'_i)+d' (y'_i,v'_i)+d' (v'_i,q'_0)\leq (1+\frac{1}{a_1}+\frac{1}{a_3})d' (y'_i,v'_i),$$
and
$$d' (y'_i,p'_0 )\leq a_1 d_{D'}(p'_0).$$ Then \eqref{eq(W-l-6'-0)} and \eqref{132} we have $$\min\{d_{D'}(q'_0),d_{D'}(p'_0)\}\geq \min\{\frac{1}{2a_1^2},\frac{1}{2a_3^2}\}d'(y_i',v_i')
>\frac{1}{2a_1^2a_3^2}d'(y_i',v_i').$$ Therefore, Lemma \ref{newlemlabel} and \eqref{li-1} lead to
\begin{equation}gin{exam}in{eqnarray*}\log \frac{d_D(q_0)}{d_D(p_{0})}&\leq& k_{D}(q_0, p_{0})
\leq M k_{D'}(q'_0,p'_0)\\
\nonumber &\leq&
4c^2M\log{\mathcal B}ig(1+\frac{d' (p'_0,q'_0)}{\min\{d_{D'}(q'_0),d_{D'}(p'_0)\}}{\mathcal B}ig)
\\
\nonumber &\leq& 4c^2M\log(6a_1^2a_3^2).\end{eqnarray*}
We infer
from \eqref{eq-11} that
\begin{equation}gin{exam}in{eqnarray}\leftarrowbel{eq-new-add2}d_D(q_0)&\leq&
(6a_1^2a_3^2)^{4c^2M} d_D(p_0)\\ \nonumber&\leq&
2(6a_1^2a_3^2)^{4c^2M} d_D(y_i)
\\ \nonumber&\leq& 2(6a_1^2a_3^2)^{4c^2M} d (y_i,y_{i+1}).\end{eqnarray}
Finally, it follows from Lemma \ref{eq-8} and the choice of $q_0$ and $u_1$ that $$k_{D}(y_i, q_0)\leq 4a^2\log{\mathcal B}ig(1+\frac{d_D(
q_0)}{d_D(y_i)}{\mathcal B}ig)\;\;{\rm
and }\;\;k_{D}(u_i, y_{i+1})\leq 4a^2\log{\mathcal B}ig(1+\frac{d_D(u_i)}{d_D(y_{i+1})}{\mathcal B}ig).$$
Then by Lemma \Ref{Lem-uniform}, \eqref{eq--7}, \eqref{eq(W-l-6'-2)} and \eqref{eq-new-add2} we get
\begin{equation}gin{eqnarray}\leftarrowbel{eq(W-l-6'-2')}
k_{D}(y_i, y_{i+1})&\leq& k_{D}(y_i, q_0)+k_{D}(q_0, u_1)+k_{D}(u_1, y_{i+1})
\\ \nonumber &\leq& 4a^2 \log{\mathcal B}ig(1+\frac{d_D(
q_0)}{d_D(y_i)}{\mathcal B}ig)+4A^2M \log{\mathcal B}ig(1+2a_3{\mathcal B}ig)
\\ \nonumber &&+4a^2 \log{\mathcal B}ig(1+\frac{d_D(
u_1)}{d_D(y_{i+1})}{\mathcal B}ig)\\
\nonumber &<& a_5 \log{\mathcal B}ig(1+\frac{ d (y_i,
y_{i+1})}{d_D(y_i)}{\mathcal B}ig),\end{eqnarray} which together with \eqref{li-newadd-2} show that $$\frac{d (y_i,y_{i+1})}{2d_D(y_i)}\leq a_5 \log{\mathcal B}ig(1+\frac{ d (y_i,y_{i+1})}{d_D(y_i)}{\mathcal B}ig).$$ A necessary condition for
this inequality is $ d (y_i, y_{i+1})\leq a_5^2d_D(y_i)$.
Hence by (\ref{eq(W-l-6'-2')}), we know that
$$k_{D}(y_i, y_{i+1})\leq a_5\log(1+a_5^2)<a_4,$$
which contradicts \eqref{eq(h-4-2)}.
Therefore, we obtain Lemma \ref{eq-0} and so Theorem \ref{thm-1}.
\section{The proof of Theorem \ref{thm-2}}
In this section, we will prove Theorem \ref{thm-2} by means of Theorem \ref{thm-1} and some results demonstrated in \cite{KLM14}. We begin by recalling necessary definitions and results.
\begin{equation}gin{defn} Let $(X, d,\mu)$ be a metric measure space. Given $Q> 1$, we say that
$X$ is {\it $Q$-regular} if there exists a constant $C>0$ such that
for each $x\in X$ and $0<r\leq {\operatorname{diam}}(X)$,
$$C^{-1}r^Q\leq \mu(B(x,r))\leq Cr^Q.$$\end{defn}
\begin{equation}gin{defn}
Let $(X,d)$ be a locally compact and rectifiably connected metric space, $D\subset X$ be a domain (an open rectifiably connected set), and $C_{gh}\geq 1$ be a constant. We say that $D$ satisfies the {\it $C_{gh}$-Gehring-Hayman inequality}, if for all $x$, $y$ in $D$ and for each
quasihyperbolic geodesic $\gamma$ joining $x$ and $y$, we have
$$\ell(\gamma)\leq C_{gh}\ell(\begin{equation}ta_{x,y}),$$
where $\begin{equation}ta_{x,y}$ is any other curve joining $x$ and $y$ in $D$. In other words, quasihyperbolic geodesics are essentially the shortest curves in $D$.
\end{defn}
\begin{equation}gin{defn}
Let $(X,d)$ be a metric space, $D\subset X$ be a domain, and $C_{bs}\geq 1$ be a constant. We say that $D$ satisfies the {\it $C_{bs}$-ball separation condition}, if for all $x$, $y$ in $D$ and for each
quasihyperbolic geodesic $\gamma$ joining $x$ and $y$, we have for every $z\in \gamma$,
$$B(z,C_{bs}d_D(z)) \cap \begin{equation}ta_{x,y} \not=\emptyset ,$$
where $\begin{equation}ta_{x,y}$ is any other curve joining $x$ and $y$ in $D$.
\end{defn}
\begin{equation}gin{defn}
Let $(X,d)$ be a metric space, $D\subset X$ be a domain and let $c\geq 1$ be a constant. We say that $D$ is
\begin{equation}gin{exam}in{enumerate} \item {\it $c$-$LLC_1$}, if for all $x\in D$ and $r>0$, we have every pair of points in $B(x,r)$ can be joined by a curve in $B(x,cr)$.
\item {\it $c$-$LLC_2$}, if for all $x\in D$ and $r>0$, we have every pair of points in $D\begin{equation}gin{array}ckslash B(x,r)$ can be joined by a curve in $D\begin{equation}gin{array}ckslash B(x,\frac{r}{c})$.
\item {\it $c$-$LLC$}, if it is both $c$-$LLC_1$ and $c$-$LLC_2$.
\end{enumerate}
Moreover, $D$ is called {\it linearly locally connected} or {$LLC$}, if it is $c$-$LLC$ for some constant $c\geq 1$.
\end{defn}
\begin{equation}gin{defn} Let $c\geq 1$. A noncomplete metric space $(X,d)$ is {\it $c$-locally externally connected} ($c$-$LEC$) provided the $c$-$LLC_2$ property holds for all points $x\in X$ and all $r\in (0,d(x)/c)$.
\end{defn}
In \cite{BH}, Buckley and Herron obtained the following interesting characterization of uniform metric spaces.
\begin{equation}gin{exam}in{Thm}\leftarrowbel{bhthm4.2}$($\cite[Theorem 4.2]{BH}$)$ A minimally nice metric space $(X, d)$ is uniform and $LEC$ if and
only if it is quasiconvex, $LLC$ with respect to curves, and satisfies a weak slice condition.
These implications are quantitative.\end{Thm}
\begin{equation}gin{defn} A metric space $(X,d)$ is called {\it annular quasiconvex}, if there is a constant $\leftarrowmbda \geq
1$ so that, for any $x\in X$ and all $0 < r' < r$, each pair of points $y, z$ in
$B(x, r) \begin{equation}gin{array}ckslash B(x, r')$ can be joined with a curve $\gamma_{yz}$ in $B(x, \leftarrowmbda r)\begin{equation}gin{array}ckslash B(x, r'/\leftarrowmbda)$
such that $\ell(\gamma_{yz})\leq \leftarrowmbda d(y, z)$.
\end{defn}
It is not difficult to see that $\leftarrowmbda$-annularly quasiconvexity property implies $C$-$LLC_2$, and hence $C$-$LEC$, where $C=2\leftarrowmbda^2$.
\subsection{The proof of Theorem \ref{thm-2}}
Necessity: Suppose that $D$ is uniform. Then we know that $D$ is John and quasiconvex. Moreover, it follows from \cite[Theorem 3.6]{BHK} that $(D,k)$ is a roughly starlike Gromov hyperbolic space because $D$ is bounded, where $k$ is the quasihyperbolic metric of $D$. It remains to show that $D$ is $LLC$. Since $X$ is $A$-annularly quasiconvex, it follows that $D$ is $LEC$. Then we deduce from Theorem \Ref{bhthm4.2} that $D$ is $LLC$.
Sufficiency: To prove the uniformity of $D$, we only need to prove that every quasihyperbolic geodesic $\gamma$ in $D$ is a uniform arc. We assume that $D$ is $c$-quasiconvex and $\delta$-hyperbolic. By \cite[Theorem 1.2]{KLM14}, we find that $D$ satisfies both the $C_{gh}$-Gehring-Hayman condition and the $C_{bs}$-ball condition for some constants $C_{gh},C_{bs}\geq 1$. So to prove the sufficiency, we only need to show that each quasihyperbolic geodesic in $D$ is a cone arc.
We first assume that $D$ is $a$-John. Since $D$ is a bounded $\delta$-hyperbolic domain of $X$, we see from \cite[Theorem 3.1]{BB03} that $(D,k)$ is $K$-roughly starlike, because $X$ is annularly quasiconvex. Then from Theorem \ref{thm-1} the uniformity of $D$ follows.
We are thus left to assume that $D$ is $c_0$-LLC. Again by virtue of the Gehring-Hayman condition, we only need to show that there is a uniform upper bound for the constant $\Leftarrowmbda$ such that
$$\min\{\ell(\gamma[x,z]),\ell(\gamma[z,y])\}=\Leftarrowmbda d_D(z)$$
for each pair of points $x,y\in D$, for any quasihyperbolic geodesic $\gamma$ in $D$ joining $x$ and $y$, and for every point $z\in \gamma$.
To this end, we deduce from the $C_{gh}$-Gehring-Hayman condition that $$\ell(\gamma[x,z])\leq cC_{gh}d(x,z)\;\;{\rm and}\;\;\ell(\gamma[y,z])\leq cC_{gh}d(y,z),$$
because the subarcs $\gamma[x,z]$ and $\gamma[x,y]$ are also quasihyperbolic geodesics.
Thus we have
$$\min\{d(x,z),d(y,z)\}\geq \frac{\Leftarrowmbda}{cC_{gh}}d_D(z).$$
On the other hand, since $D$ is $c_0$-LLC, we know that there is a curve $\begin{equation}ta$ joining $x$ to $y$ with
\begin{equation}gin{eqnarray}\leftarrowbel{eq-new1}\begin{equation}ta\subset X\setminus \overline{B}(z,\frac{\Leftarrowmbda}{cc_0C_{gh}}d_D(z)).\end{eqnarray}
Furthermore, since $\gamma$ is a quasihyperbolic geodesic and $D$ satisfies the $C_{bs}$-ball separation condition, we see that $$\begin{equation}ta\cap B(z,C_{bs}d_D(z))\not=\emptyset,$$ which together with \eqref{eq-new1} show that
$$\Leftarrowmbda\leq cc_0C_{gh}C_{bs},$$
as required.
Hence, the proof of Theorem \ref{thm-2} is complete.
\begin{equation}gin{exam}in{thebibliography}{99}
\bibitem{BB03} {\sc Z. M. Balogh and S. M. Buckley}, Geometric characterizations of Gromov hyperbolicity, \textit{Invent. Math.} {\bf 153} (2003), 261--301.
\bibitem{BHK} {\sc M. Bonk, J. Heinonen and P. Koskela}, Uniformizing Gromov hyperbolic domains, \textit{Ast\'erisque} {\bf 270} (2001), 1--99.
\bibitem{BH} {\sc S. Buckley and D. Herron}, Uniform spaces and weak slice spaces,
\textit{Conform. Geom. Dyn.} {\bf 11} (2007), 191--206 (electronic).
\bibitem{BHX} {\sc S. M. Buckley, D. Herron and X. Xie}, Metric space inversions, quasihyperbolic distance, and uniform spaces, \textit{Indiana Univ. Math. J.} {\bf
57} (2008), 837--890.
\bibitem{CP17} {\sc S. Chen and S. Ponnusamy}, John disks and K-quasiconformal harmonic mappings, \textit{J. Geom. Anal.} {\bf 27} (2017), 1468--1488.
\bibitem{GHM} {\sc F. W. Gehring, K. Hag and O. Martio}, Quasihyperbolic geodesics in John domains, \textit{Math. Scand.} {\bf 36} (1989), 75--92.
\bibitem{GO} {\sc F. W. Gehring and B. G. Osgood}, Uniform domains and the quasi-hyperbolic metric, \textit{J. Analyse Math.} {\bf 36} (1979), 50--74.
\bibitem{GP76} {\sc F. W. Gehring and B. P. Palka}, Quasiconformally homogeneous domains, \textit{J. Analyse Math.} {\bf 30} (1976), 172--199.
\bibitem{GNV94} {\sc M. Ghamsari, R. N\"{a}kki and J. V\"{a}is\"{a}l\"{a}}, John disks and extension of maps, \textit{Monatsh. Math.} {\bf 117} (1994), 63--94.
\bibitem{GGKN17} {\sc P. Goldstein, C. Guo, P. Koskela and D. Nandi}, Characterizations of generalized John domains in $\mathbb {R}^ n$ via metric duality, \textit{arXiv preprint arXiv:1710.02050,} 2017.
\bibitem{Guo15} {\sc Ch. Guo}, Uniform continuity of quasiconformal mappings onto generalized John domains, \textit{Ann. Acad. Sci. Fenn. Math.} {\bf 40} (2015), 183--202.
\bibitem{Hei89} {\sc J. Heinonen}, Quasiconformal mappings onto John domains, \textit{Rev. Math. Iber.} {\bf 5} (1989), 97--123.
\bibitem{HK} {\sc J. Heinonen and P. Koskela}, Quasiconformal maps in metric spaces with controlled geometry, \textit{Acta Math.} {\bf 181} (1998), 1--61.
\bibitem{HR93} {\sc J. Heinonen and S. Rohde}, The Gehring-Hayman inequality for quasihyperbolic geodesics, \textit{Math. Proc. Camb. Phil. Soc.} {\bf 114} (1993), 393--405.
\bibitem{Jo61} {\sc F. John}, Rotation and strain, \textit{Comm. Pure. Appl. Math.} {\bf 14} (1961), 391--413.
\bibitem{KLM14} {\sc P. Koskela, P. Lammi and V. Manojlovi\'c}, Gromov hyperbolicity and quasihyperbolic geodesics, \textit{Ann. Sci. \'Ec. Norm. Sup\'er.} {\bf 47} (2014), 975--990.
\bibitem{Li} {\sc Y. Li,} Neargeodesic in John domain in Banach spaces, \textit{Internat. J. Math.} {\bf 25} (5) (2014), 1450041 (17 pages), doi: 101142/S0129167X14500414.
\bibitem{LVZ17} {\sc Y. Li, M. Vuorinen and Q. Zhou}, Characterizations of John spaces, \textit{Monatsh. Math.,} 2018, https://doi.org/10.1007/s00605-018-1231-6.
\bibitem{LVZ2} {\sc Y. Li, M. Vuorinen and Q. Zhou}, Weakly quasisymmetric maps and uniform spaces, \textit{Comput. Methods Funct. Theory,} {\bf 18} 2018, 689-715.
\bibitem{MS78} {\sc O. Martio and J. Sarvas}, Injectivity theorems in plane and space, \textit{Ann. Acad. Sci. Fenn. Ser. A I Math.} {\bf 4} (1978), 383--401.
\bibitem{NV} {\sc R. N\"{a}kki and J. V\"{a}is\"{a}l\"{a}}, John disks,
\textit{Expo. Math.} {\bf 9} (1991), 3--43.
\bibitem{RT2}
{\sc A. Rasila and J. Talponen},
{On quasihyperbolic geodesics in Banach spaces.} {\it Ann. Acad. Sci. Fenn. Math.} {\bf 39} (1) (2014), 163--173.
\bibitem{Vai6} {\sc J. V\"{a}is\"{a}l\"{a}}, Free quasiconformality
in Banach spaces. II, \textit{Ann. Acad. Sci. Fenn. Ser. A I Math.}
{\bf 16} (1991), 255--310.
\bibitem{Vai05} {\sc J. V\"{a}is\"{a}l\"{a}}, Hyperbolic and
uniform domains in Banach spaces, \textit{Ann. Acad. Sci. Fenn. Math.}
{\bf 30} (2005), 261--302.
\bibitem{ZR} {\sc J. V\"{a}is\"{a}l\"{a}}, Hyperbolic and
uniform domains in Banach spaces, \textit{Ann. Acad. Sci. Fenn. Math.}
{\bf 30} (2005), 261--302.
\end{thebibliography}
\end{document} | math |
गाजियाबाद: नौकरी का झांसा देकर हिंदू दल के पदाधिकारी ने किया युवती से रेप !!
गाजियाबाद के सिहानी थाना क्षेत्र के गांधीनगर इलाके में स्थित एक होटल में युवती से रेप का मामला सामने आया है| इस होटल में आरोपी एक युवती को नौकरी दिलाने का झांसा देकर लाया था| वहीं रात को आरोपी ने पीड़िता को कोल्ड ड्रिंक में नशीला पदार्थ पिलाकर उसके साथ दुष्कर्म किया, पीड़िता की शिकायत पर पुलिस ने आरोपी को गिरफ्तार कर जांच शुरू कर दी है|
पीड़िता का आरोप है कि वह अपनी सहेली के माध्यम से आरोपी के बारे में पता चला था और आरोपी ने ये भरोसा दिलाया था कि वह उसकी नौकरी लगवा देगा| जिसके बाद आरोपी ने होटल में बुलाकर उसके साथ दुष्कर्म किया. इसके बाद पीड़िता ने होटल के रिसेप्शन से ही अपनी बहन को फोन किया और किसी तरह से पुलिस तक पहुंची.
पीड़िता की शिकायत पर पुलिस ने मामला दर्ज कर लिया है और जांच में जुट गई है, बताया जा रहा है कि आरोपी का नाम अंकुर त्यागी है. आरोपी के बारे में बताया जा रहा है कि वह एक हिंदू दल का पदाधिकारी है, हालांकि पुलिस का कहना है कि इस बात का जिक्र तहरीर में नहीं किया गया है. पीड़ित युवती का यह भी आरोप है कि उसे गन प्वाइंट पर धमकाया जा रहा है.
युवती के मुताबिक उसे डराते हुए यह भी कहा गया था कि उसका अश्लील वीडियो बना लिया गया है| घटना के बाद से पीड़िता सहमी हुई है और ज्यादा कुछ बताने की स्थिति में नहीं है. पीड़ित युवती कुछ महीने पहले से ही आरोपी को जानती थी. फिलहाल पीड़िता शिकायत पर पुलिस ने मामला दर्ज कर लिया है और जांच जारी है | | hindi |
<?xml version="1.0" ?><!DOCTYPE TS><TS language="fi" version="2.0">
<defaultcodec>UTF-8</defaultcodec>
<context>
<name>AboutDialog</name>
<message>
<location filename="../forms/aboutdialog.ui" line="+14"/>
<source>About Academiccoin</source>
<translation>Tietoa Academiccoinista</translation>
</message>
<message>
<location line="+39"/>
<source><b>Academiccoin</b> version</source>
<translation><b>Academiccoin</b> versio</translation>
</message>
<message>
<location line="+57"/>
<source>
This is experimental software.
Distributed under the MIT/X11 software license, see the accompanying file COPYING or http://www.opensource.org/licenses/mit-license.php.
This product includes software developed by the OpenSSL Project for use in the OpenSSL Toolkit (http://www.openssl.org/) and cryptographic software written by Eric Young (eay@cryptsoft.com) and UPnP software written by Thomas Bernard.</source>
<translation>
Tämä on kokeellinen ohjelmisto.
Levitetään MIT/X11 ohjelmistolisenssin alaisuudessa. Tarkemmat tiedot löytyvät tiedostosta COPYING tai osoitteesta http://www.opensource.org/licenses/mit-license.php.
Tämä ohjelma sisältää OpenSSL projektin OpenSSL työkalupakin (http://www.openssl.org/), Eric Youngin (eay@cryptsoft.com) kehittämän salausohjelmiston sekä Thomas Bernardin UPnP ohjelmiston.
</translation>
</message>
<message>
<location filename="../aboutdialog.cpp" line="+14"/>
<source>Copyright</source>
<translation>Tekijänoikeus</translation>
</message>
<message>
<location line="+0"/>
<source>The Academiccoin developers</source>
<translation type="unfinished"/>
</message>
</context>
<context>
<name>AddressBookPage</name>
<message>
<location filename="../forms/addressbookpage.ui" line="+14"/>
<source>Address Book</source>
<translation>Osoitekirja</translation>
</message>
<message>
<location line="+19"/>
<source>Double-click to edit address or label</source>
<translation>Kaksoisnapauta muokataksesi osoitetta tai nimeä</translation>
</message>
<message>
<location line="+27"/>
<source>Create a new address</source>
<translation>Luo uusi osoite</translation>
</message>
<message>
<location line="+14"/>
<source>Copy the currently selected address to the system clipboard</source>
<translation>Kopioi valittu osoite leikepöydälle</translation>
</message>
<message>
<location line="-11"/>
<source>&New Address</source>
<translation>&Uusi Osoite</translation>
</message>
<message>
<location filename="../addressbookpage.cpp" line="+63"/>
<source>These are your Academiccoin addresses for receiving payments. You may want to give a different one to each sender so you can keep track of who is paying you.</source>
<translation>Nämä ovat Academiccoin-osoitteesi joihin voit vastaanottaa maksuja. Voit haluta antaa jokaiselle maksajalle omansa, että pystyt seuraamaan keneltä maksut tulevat.</translation>
</message>
<message>
<location filename="../forms/addressbookpage.ui" line="+14"/>
<source>&Copy Address</source>
<translation>&Kopioi Osoite</translation>
</message>
<message>
<location line="+11"/>
<source>Show &QR Code</source>
<translation>Näytä &QR-koodi</translation>
</message>
<message>
<location line="+11"/>
<source>Sign a message to prove you own a Academiccoin address</source>
<translation>Allekirjoita viesti todistaaksesi, että omistat Academiccoin-osoitteen</translation>
</message>
<message>
<location line="+3"/>
<source>Sign &Message</source>
<translation>Allekirjoita &viesti</translation>
</message>
<message>
<location line="+25"/>
<source>Delete the currently selected address from the list</source>
<translation>Poista valittu osoite listalta</translation>
</message>
<message>
<location line="+27"/>
<source>Export the data in the current tab to a file</source>
<translation>Vie auki olevan välilehden tiedot tiedostoon</translation>
</message>
<message>
<location line="+3"/>
<source>&Export</source>
<translation type="unfinished"/>
</message>
<message>
<location line="-44"/>
<source>Verify a message to ensure it was signed with a specified Academiccoin address</source>
<translation>Tarkista viestin allekirjoitus varmistaaksesi, että se allekirjoitettiin tietyllä Academiccoin-osoitteella</translation>
</message>
<message>
<location line="+3"/>
<source>&Verify Message</source>
<translation>&Varmista viesti...</translation>
</message>
<message>
<location line="+14"/>
<source>&Delete</source>
<translation>&Poista</translation>
</message>
<message>
<location filename="../addressbookpage.cpp" line="-5"/>
<source>These are your Academiccoin addresses for sending payments. Always check the amount and the receiving address before sending coins.</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+13"/>
<source>Copy &Label</source>
<translation>Kopioi &Nimi</translation>
</message>
<message>
<location line="+1"/>
<source>&Edit</source>
<translation>&Muokkaa</translation>
</message>
<message>
<location line="+1"/>
<source>Send &Coins</source>
<translation>Lähetä &Rahaa</translation>
</message>
<message>
<location line="+260"/>
<source>Export Address Book Data</source>
<translation>Vie osoitekirja</translation>
</message>
<message>
<location line="+1"/>
<source>Comma separated file (*.csv)</source>
<translation>Comma separated file (*.csv)</translation>
</message>
<message>
<location line="+13"/>
<source>Error exporting</source>
<translation>Virhe viedessä osoitekirjaa</translation>
</message>
<message>
<location line="+0"/>
<source>Could not write to file %1.</source>
<translation>Ei voida kirjoittaa tiedostoon %1.</translation>
</message>
</context>
<context>
<name>AddressTableModel</name>
<message>
<location filename="../addresstablemodel.cpp" line="+144"/>
<source>Label</source>
<translation>Nimi</translation>
</message>
<message>
<location line="+0"/>
<source>Address</source>
<translation>Osoite</translation>
</message>
<message>
<location line="+36"/>
<source>(no label)</source>
<translation>(ei nimeä)</translation>
</message>
</context>
<context>
<name>AskPassphraseDialog</name>
<message>
<location filename="../forms/askpassphrasedialog.ui" line="+26"/>
<source>Passphrase Dialog</source>
<translation>Tunnuslauseen Dialogi</translation>
</message>
<message>
<location line="+21"/>
<source>Enter passphrase</source>
<translation>Kirjoita tunnuslause</translation>
</message>
<message>
<location line="+14"/>
<source>New passphrase</source>
<translation>Uusi tunnuslause</translation>
</message>
<message>
<location line="+14"/>
<source>Repeat new passphrase</source>
<translation>Kiroita uusi tunnuslause uudelleen</translation>
</message>
<message>
<location filename="../askpassphrasedialog.cpp" line="+33"/>
<source>Enter the new passphrase to the wallet.<br/>Please use a passphrase of <b>10 or more random characters</b>, or <b>eight or more words</b>.</source>
<translation>Anna lompakolle uusi tunnuslause.<br/>Käytä tunnuslausetta, jossa on ainakin <b>10 satunnaista mekkiä</b> tai <b>kahdeksan sanaa</b>.</translation>
</message>
<message>
<location line="+1"/>
<source>Encrypt wallet</source>
<translation>Salaa lompakko</translation>
</message>
<message>
<location line="+3"/>
<source>This operation needs your wallet passphrase to unlock the wallet.</source>
<translation>Tätä toimintoa varten sinun täytyy antaa lompakon tunnuslause sen avaamiseksi.</translation>
</message>
<message>
<location line="+5"/>
<source>Unlock wallet</source>
<translation>Avaa lompakko</translation>
</message>
<message>
<location line="+3"/>
<source>This operation needs your wallet passphrase to decrypt the wallet.</source>
<translation>Tätä toimintoa varten sinun täytyy antaa lompakon tunnuslause salauksen purkuun.</translation>
</message>
<message>
<location line="+5"/>
<source>Decrypt wallet</source>
<translation>Pura lompakon salaus</translation>
</message>
<message>
<location line="+3"/>
<source>Change passphrase</source>
<translation>Vaihda tunnuslause</translation>
</message>
<message>
<location line="+1"/>
<source>Enter the old and new passphrase to the wallet.</source>
<translation>Anna vanha ja uusi tunnuslause.</translation>
</message>
<message>
<location line="+46"/>
<source>Confirm wallet encryption</source>
<translation>Vahvista lompakon salaus</translation>
</message>
<message>
<location line="+1"/>
<source>Warning: If you encrypt your wallet and lose your passphrase, you will <b>LOSE ALL OF YOUR BITCOINS</b>!</source>
<translation>Varoitus: Jos salaat lompakkosi ja menetät tunnuslauseesi, <b>MENETÄT KAIKKI BITCOINISI</b>!</translation>
</message>
<message>
<location line="+0"/>
<source>Are you sure you wish to encrypt your wallet?</source>
<translation>Haluatko varmasti salata lompakkosi?</translation>
</message>
<message>
<location line="+15"/>
<source>IMPORTANT: Any previous backups you have made of your wallet file should be replaced with the newly generated, encrypted wallet file. For security reasons, previous backups of the unencrypted wallet file will become useless as soon as you start using the new, encrypted wallet.</source>
<translation>TÄRKEÄÄ: Kaikki vanhat lompakon varmuuskopiot pitäisi korvata uusilla suojatuilla varmuuskopioilla. Turvallisuussyistä edelliset varmuuskopiot muuttuvat turhiksi, kun aloitat suojatun lompakon käytön.</translation>
</message>
<message>
<location line="+100"/>
<location line="+24"/>
<source>Warning: The Caps Lock key is on!</source>
<translation>Varoitus: Caps Lock on käytössä!</translation>
</message>
<message>
<location line="-130"/>
<location line="+58"/>
<source>Wallet encrypted</source>
<translation>Lompakko salattu</translation>
</message>
<message>
<location line="-56"/>
<source>Academiccoin will close now to finish the encryption process. Remember that encrypting your wallet cannot fully protect your academiccoins from being stolen by malware infecting your computer.</source>
<translation>Academiccoin sulkeutuu lopettaakseen salausprosessin. Muista, että salattukaan lompakko ei täysin suojaa sitä haittaohjelmien aiheuttamilta varkauksilta.</translation>
</message>
<message>
<location line="+13"/>
<location line="+7"/>
<location line="+42"/>
<location line="+6"/>
<source>Wallet encryption failed</source>
<translation>Lompakon salaus epäonnistui</translation>
</message>
<message>
<location line="-54"/>
<source>Wallet encryption failed due to an internal error. Your wallet was not encrypted.</source>
<translation>Lompakon salaaminen epäonnistui sisäisen virheen vuoksi. Lompakkoasi ei salattu.</translation>
</message>
<message>
<location line="+7"/>
<location line="+48"/>
<source>The supplied passphrases do not match.</source>
<translation>Annetut tunnuslauseet eivät täsmää.</translation>
</message>
<message>
<location line="-37"/>
<source>Wallet unlock failed</source>
<translation>Lompakon avaaminen epäonnistui.</translation>
</message>
<message>
<location line="+1"/>
<location line="+11"/>
<location line="+19"/>
<source>The passphrase entered for the wallet decryption was incorrect.</source>
<translation>Annettu tunnuslause oli väärä.</translation>
</message>
<message>
<location line="-20"/>
<source>Wallet decryption failed</source>
<translation>Lompakon salauksen purku epäonnistui.</translation>
</message>
<message>
<location line="+14"/>
<source>Wallet passphrase was successfully changed.</source>
<translation>Lompakon tunnuslause vaihdettiin onnistuneesti.</translation>
</message>
</context>
<context>
<name>AcademiccoinGUI</name>
<message>
<location filename="../academiccoingui.cpp" line="+233"/>
<source>Sign &message...</source>
<translation>&Allekirjoita viesti...</translation>
</message>
<message>
<location line="+280"/>
<source>Synchronizing with network...</source>
<translation>Synkronoidaan verkon kanssa...</translation>
</message>
<message>
<location line="-349"/>
<source>&Overview</source>
<translation>&Yleisnäkymä</translation>
</message>
<message>
<location line="+1"/>
<source>Show general overview of wallet</source>
<translation>Lompakon tilanteen yleiskatsaus</translation>
</message>
<message>
<location line="+20"/>
<source>&Transactions</source>
<translation>&Rahansiirrot</translation>
</message>
<message>
<location line="+1"/>
<source>Browse transaction history</source>
<translation>Selaa rahansiirtohistoriaa</translation>
</message>
<message>
<location line="+7"/>
<source>Edit the list of stored addresses and labels</source>
<translation>Muokkaa tallennettujen nimien ja osoitteiden listaa</translation>
</message>
<message>
<location line="-14"/>
<source>Show the list of addresses for receiving payments</source>
<translation>Näytä Academiccoinien vastaanottamiseen käytetyt osoitteet</translation>
</message>
<message>
<location line="+31"/>
<source>E&xit</source>
<translation>L&opeta</translation>
</message>
<message>
<location line="+1"/>
<source>Quit application</source>
<translation>Sulje ohjelma</translation>
</message>
<message>
<location line="+4"/>
<source>Show information about Academiccoin</source>
<translation>Näytä tietoa Academiccoin-projektista</translation>
</message>
<message>
<location line="+2"/>
<source>About &Qt</source>
<translation>Tietoja &Qt</translation>
</message>
<message>
<location line="+1"/>
<source>Show information about Qt</source>
<translation>Näytä tietoja QT:ta</translation>
</message>
<message>
<location line="+2"/>
<source>&Options...</source>
<translation>&Asetukset...</translation>
</message>
<message>
<location line="+6"/>
<source>&Encrypt Wallet...</source>
<translation>&Salaa lompakko...</translation>
</message>
<message>
<location line="+3"/>
<source>&Backup Wallet...</source>
<translation>&Varmuuskopioi Lompakko...</translation>
</message>
<message>
<location line="+2"/>
<source>&Change Passphrase...</source>
<translation>&Vaihda Tunnuslause...</translation>
</message>
<message>
<location line="+285"/>
<source>Importing blocks from disk...</source>
<translation>Tuodaan lohkoja levyltä</translation>
</message>
<message>
<location line="+3"/>
<source>Reindexing blocks on disk...</source>
<translation>Ladataan lohkoindeksiä...</translation>
</message>
<message>
<location line="-347"/>
<source>Send coins to a Academiccoin address</source>
<translation>Lähetä kolikoita Academiccoin-osoitteeseen</translation>
</message>
<message>
<location line="+49"/>
<source>Modify configuration options for Academiccoin</source>
<translation>Muuta Academiccoinin konfiguraatioasetuksia</translation>
</message>
<message>
<location line="+9"/>
<source>Backup wallet to another location</source>
<translation>Varmuuskopioi lompakko toiseen sijaintiin</translation>
</message>
<message>
<location line="+2"/>
<source>Change the passphrase used for wallet encryption</source>
<translation>Vaihda lompakon salaukseen käytettävä tunnuslause</translation>
</message>
<message>
<location line="+6"/>
<source>&Debug window</source>
<translation>&Testausikkuna</translation>
</message>
<message>
<location line="+1"/>
<source>Open debugging and diagnostic console</source>
<translation>Avaa debuggaus- ja diagnostiikkakonsoli</translation>
</message>
<message>
<location line="-4"/>
<source>&Verify message...</source>
<translation>Varmista &viesti...</translation>
</message>
<message>
<location line="-165"/>
<location line="+530"/>
<source>Academiccoin</source>
<translation>Academiccoin</translation>
</message>
<message>
<location line="-530"/>
<source>Wallet</source>
<translation>Lompakko</translation>
</message>
<message>
<location line="+101"/>
<source>&Send</source>
<translation>&Lähetä</translation>
</message>
<message>
<location line="+7"/>
<source>&Receive</source>
<translation>&Vastaanota</translation>
</message>
<message>
<location line="+14"/>
<source>&Addresses</source>
<translation>&Osoitteet</translation>
</message>
<message>
<location line="+22"/>
<source>&About Academiccoin</source>
<translation>&Tietoa Academiccoinista</translation>
</message>
<message>
<location line="+9"/>
<source>&Show / Hide</source>
<translation>&Näytä / Piilota</translation>
</message>
<message>
<location line="+1"/>
<source>Show or hide the main Window</source>
<translation>Näytä tai piilota Academiccoin-ikkuna</translation>
</message>
<message>
<location line="+3"/>
<source>Encrypt the private keys that belong to your wallet</source>
<translation>Suojaa yksityiset avaimet, jotka kuuluvat lompakkoosi</translation>
</message>
<message>
<location line="+7"/>
<source>Sign messages with your Academiccoin addresses to prove you own them</source>
<translation>Allekirjoita viestisi omalla Academiccoin -osoitteellasi todistaaksesi, että omistat ne</translation>
</message>
<message>
<location line="+2"/>
<source>Verify messages to ensure they were signed with specified Academiccoin addresses</source>
<translation>Varmista, että viestisi on allekirjoitettu määritetyllä Academiccoin -osoitteella</translation>
</message>
<message>
<location line="+28"/>
<source>&File</source>
<translation>&Tiedosto</translation>
</message>
<message>
<location line="+7"/>
<source>&Settings</source>
<translation>&Asetukset</translation>
</message>
<message>
<location line="+6"/>
<source>&Help</source>
<translation>&Apua</translation>
</message>
<message>
<location line="+9"/>
<source>Tabs toolbar</source>
<translation>Välilehtipalkki</translation>
</message>
<message>
<location line="+17"/>
<location line="+10"/>
<source>[testnet]</source>
<translation>[testnet]</translation>
</message>
<message>
<location line="+47"/>
<source>Academiccoin client</source>
<translation>Academiccoin-asiakas</translation>
</message>
<message numerus="yes">
<location line="+141"/>
<source>%n active connection(s) to Academiccoin network</source>
<translation><numerusform>%n aktiivinen yhteys Academiccoin-verkkoon</numerusform><numerusform>%n aktiivista yhteyttä Academiccoin-verkkoon</numerusform></translation>
</message>
<message>
<location line="+22"/>
<source>No block source available...</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+12"/>
<source>Processed %1 of %2 (estimated) blocks of transaction history.</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+4"/>
<source>Processed %1 blocks of transaction history.</source>
<translation>Käsitelty %1 lohkoa rahansiirtohistoriasta</translation>
</message>
<message numerus="yes">
<location line="+20"/>
<source>%n hour(s)</source>
<translation><numerusform>%n tunti</numerusform><numerusform>%n tuntia</numerusform></translation>
</message>
<message numerus="yes">
<location line="+4"/>
<source>%n day(s)</source>
<translation type="unfinished"><numerusform></numerusform><numerusform></numerusform></translation>
</message>
<message numerus="yes">
<location line="+4"/>
<source>%n week(s)</source>
<translation><numerusform>%n viikko</numerusform><numerusform>%n viikkoa</numerusform></translation>
</message>
<message>
<location line="+4"/>
<source>%1 behind</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+14"/>
<source>Last received block was generated %1 ago.</source>
<translation>Viimeisin vastaanotettu lohko tuotettu %1.</translation>
</message>
<message>
<location line="+2"/>
<source>Transactions after this will not yet be visible.</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+22"/>
<source>Error</source>
<translation>Virhe</translation>
</message>
<message>
<location line="+3"/>
<source>Warning</source>
<translation>Varoitus</translation>
</message>
<message>
<location line="+3"/>
<source>Information</source>
<translation>Tietoa</translation>
</message>
<message>
<location line="+70"/>
<source>This transaction is over the size limit. You can still send it for a fee of %1, which goes to the nodes that process your transaction and helps to support the network. Do you want to pay the fee?</source>
<translation type="unfinished"/>
</message>
<message>
<location line="-140"/>
<source>Up to date</source>
<translation>Rahansiirtohistoria on ajan tasalla</translation>
</message>
<message>
<location line="+31"/>
<source>Catching up...</source>
<translation>Saavutetaan verkkoa...</translation>
</message>
<message>
<location line="+113"/>
<source>Confirm transaction fee</source>
<translation>Vahvista maksukulu</translation>
</message>
<message>
<location line="+8"/>
<source>Sent transaction</source>
<translation>Lähetetyt rahansiirrot</translation>
</message>
<message>
<location line="+0"/>
<source>Incoming transaction</source>
<translation>Saapuva rahansiirto</translation>
</message>
<message>
<location line="+1"/>
<source>Date: %1
Amount: %2
Type: %3
Address: %4
</source>
<translation>Päivä: %1
Määrä: %2
Tyyppi: %3
Osoite: %4</translation>
</message>
<message>
<location line="+33"/>
<location line="+23"/>
<source>URI handling</source>
<translation>URI käsittely</translation>
</message>
<message>
<location line="-23"/>
<location line="+23"/>
<source>URI can not be parsed! This can be caused by an invalid Academiccoin address or malformed URI parameters.</source>
<translation>URIa ei voitu jäsentää! Tämä voi johtua kelvottomasta Academiccoin-osoitteesta tai virheellisistä URI parametreista.</translation>
</message>
<message>
<location line="+17"/>
<source>Wallet is <b>encrypted</b> and currently <b>unlocked</b></source>
<translation>Lompakko on <b>salattu</b> ja tällä hetkellä <b>avoinna</b></translation>
</message>
<message>
<location line="+8"/>
<source>Wallet is <b>encrypted</b> and currently <b>locked</b></source>
<translation>Lompakko on <b>salattu</b> ja tällä hetkellä <b>lukittuna</b></translation>
</message>
<message>
<location filename="../academiccoin.cpp" line="+111"/>
<source>A fatal error occurred. Academiccoin can no longer continue safely and will quit.</source>
<translation>Peruuttamaton virhe on tapahtunut. Academiccoin ei voi enää jatkaa turvallisesti ja sammutetaan.</translation>
</message>
</context>
<context>
<name>ClientModel</name>
<message>
<location filename="../clientmodel.cpp" line="+104"/>
<source>Network Alert</source>
<translation>Verkkohälytys</translation>
</message>
</context>
<context>
<name>EditAddressDialog</name>
<message>
<location filename="../forms/editaddressdialog.ui" line="+14"/>
<source>Edit Address</source>
<translation>Muokkaa osoitetta</translation>
</message>
<message>
<location line="+11"/>
<source>&Label</source>
<translation>&Nimi</translation>
</message>
<message>
<location line="+10"/>
<source>The label associated with this address book entry</source>
<translation>Tähän osoitteeseen liitetty nimi</translation>
</message>
<message>
<location line="+7"/>
<source>&Address</source>
<translation>&Osoite</translation>
</message>
<message>
<location line="+10"/>
<source>The address associated with this address book entry. This can only be modified for sending addresses.</source>
<translation>Osoite, joka liittyy tämän osoitekirjan merkintään. Tätä voidaan muuttaa vain lähtevissä osoitteissa.</translation>
</message>
<message>
<location filename="../editaddressdialog.cpp" line="+21"/>
<source>New receiving address</source>
<translation>Uusi vastaanottava osoite</translation>
</message>
<message>
<location line="+4"/>
<source>New sending address</source>
<translation>Uusi lähettävä osoite</translation>
</message>
<message>
<location line="+3"/>
<source>Edit receiving address</source>
<translation>Muokkaa vastaanottajan osoitetta</translation>
</message>
<message>
<location line="+4"/>
<source>Edit sending address</source>
<translation>Muokkaa lähtevää osoitetta</translation>
</message>
<message>
<location line="+76"/>
<source>The entered address "%1" is already in the address book.</source>
<translation>Osoite "%1" on jo osoitekirjassa.</translation>
</message>
<message>
<location line="-5"/>
<source>The entered address "%1" is not a valid Academiccoin address.</source>
<translation>Antamasi osoite "%1" ei ole validi Academiccoin-osoite.</translation>
</message>
<message>
<location line="+10"/>
<source>Could not unlock wallet.</source>
<translation>Lompakkoa ei voitu avata.</translation>
</message>
<message>
<location line="+5"/>
<source>New key generation failed.</source>
<translation>Uuden avaimen luonti epäonnistui.</translation>
</message>
</context>
<context>
<name>GUIUtil::HelpMessageBox</name>
<message>
<location filename="../guiutil.cpp" line="+424"/>
<location line="+12"/>
<source>Academiccoin-Qt</source>
<translation>Academiccoin-Qt</translation>
</message>
<message>
<location line="-12"/>
<source>version</source>
<translation>versio</translation>
</message>
<message>
<location line="+2"/>
<source>Usage:</source>
<translation>Käyttö:</translation>
</message>
<message>
<location line="+1"/>
<source>command-line options</source>
<translation>komentorivi parametrit</translation>
</message>
<message>
<location line="+4"/>
<source>UI options</source>
<translation>Käyttöliittymäasetukset</translation>
</message>
<message>
<location line="+1"/>
<source>Set language, for example "de_DE" (default: system locale)</source>
<translation>Set language, for example "de_DE" (default: system locale)</translation>
</message>
<message>
<location line="+1"/>
<source>Start minimized</source>
<translation>Käynnistä pienennettynä</translation>
</message>
<message>
<location line="+1"/>
<source>Show splash screen on startup (default: 1)</source>
<translation>Näytä aloitusruutu käynnistettäessä (oletus: 1)</translation>
</message>
</context>
<context>
<name>OptionsDialog</name>
<message>
<location filename="../forms/optionsdialog.ui" line="+14"/>
<source>Options</source>
<translation>Asetukset</translation>
</message>
<message>
<location line="+16"/>
<source>&Main</source>
<translation>&Yleiset</translation>
</message>
<message>
<location line="+6"/>
<source>Optional transaction fee per kB that helps make sure your transactions are processed quickly. Most transactions are 1 kB.</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+15"/>
<source>Pay transaction &fee</source>
<translation>Maksa rahansiirtopalkkio</translation>
</message>
<message>
<location line="+31"/>
<source>Automatically start Academiccoin after logging in to the system.</source>
<translation>Käynnistä Academiccoin kirjautumisen yhteydessä.</translation>
</message>
<message>
<location line="+3"/>
<source>&Start Academiccoin on system login</source>
<translation>&Käynnistä Academiccoin kirjautumisen yhteydessä</translation>
</message>
<message>
<location line="+35"/>
<source>Reset all client options to default.</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+3"/>
<source>&Reset Options</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+13"/>
<source>&Network</source>
<translation>&Verkko</translation>
</message>
<message>
<location line="+6"/>
<source>Automatically open the Academiccoin client port on the router. This only works when your router supports UPnP and it is enabled.</source>
<translation>Avaa Academiccoin-asiakasohjelman portti reitittimellä automaattisesti. Tämä toimii vain, jos reitittimesi tukee UPnP:tä ja se on käytössä.</translation>
</message>
<message>
<location line="+3"/>
<source>Map port using &UPnP</source>
<translation>Portin uudelleenohjaus &UPnP:llä</translation>
</message>
<message>
<location line="+7"/>
<source>Connect to the Academiccoin network through a SOCKS proxy (e.g. when connecting through Tor).</source>
<translation>Ota yhteys Academiccoin-verkkoon SOCKS-proxyn läpi (esimerkiksi kun haluat käyttää Tor-verkkoa).</translation>
</message>
<message>
<location line="+3"/>
<source>&Connect through SOCKS proxy:</source>
<translation>&Ota yhteys SOCKS-proxyn kautta:</translation>
</message>
<message>
<location line="+9"/>
<source>Proxy &IP:</source>
<translation>Proxyn &IP:</translation>
</message>
<message>
<location line="+19"/>
<source>IP address of the proxy (e.g. 127.0.0.1)</source>
<translation>Välityspalvelimen IP-osoite (esim. 127.0.0.1)</translation>
</message>
<message>
<location line="+7"/>
<source>&Port:</source>
<translation>&Portti</translation>
</message>
<message>
<location line="+19"/>
<source>Port of the proxy (e.g. 9050)</source>
<translation>Proxyn Portti (esim. 9050)</translation>
</message>
<message>
<location line="+7"/>
<source>SOCKS &Version:</source>
<translation>SOCKS &Versio:</translation>
</message>
<message>
<location line="+13"/>
<source>SOCKS version of the proxy (e.g. 5)</source>
<translation>Proxyn SOCKS-versio (esim. 5)</translation>
</message>
<message>
<location line="+36"/>
<source>&Window</source>
<translation>&Ikkuna</translation>
</message>
<message>
<location line="+6"/>
<source>Show only a tray icon after minimizing the window.</source>
<translation>Näytä ainoastaan ilmaisinalueella ikkunan pienentämisen jälkeen.</translation>
</message>
<message>
<location line="+3"/>
<source>&Minimize to the tray instead of the taskbar</source>
<translation>&Pienennä ilmaisinalueelle työkalurivin sijasta</translation>
</message>
<message>
<location line="+7"/>
<source>Minimize instead of exit the application when the window is closed. When this option is enabled, the application will be closed only after selecting Quit in the menu.</source>
<translation>Ikkunaa suljettaessa vain pienentää Academiccoin-ohjelman ikkunan lopettamatta itse ohjelmaa. Kun tämä asetus on valittuna, ohjelman voi sulkea vain valitsemalla Lopeta ohjelman valikosta.</translation>
</message>
<message>
<location line="+3"/>
<source>M&inimize on close</source>
<translation>P&ienennä suljettaessa</translation>
</message>
<message>
<location line="+21"/>
<source>&Display</source>
<translation>&Käyttöliittymä</translation>
</message>
<message>
<location line="+8"/>
<source>User Interface &language:</source>
<translation>&Käyttöliittymän kieli</translation>
</message>
<message>
<location line="+13"/>
<source>The user interface language can be set here. This setting will take effect after restarting Academiccoin.</source>
<translation>Tässä voit määritellä käyttöliittymän kielen. Muutokset astuvat voimaan seuraavan kerran, kun Academiccoin käynnistetään.</translation>
</message>
<message>
<location line="+11"/>
<source>&Unit to show amounts in:</source>
<translation>Yksikkö jona academiccoin-määrät näytetään</translation>
</message>
<message>
<location line="+13"/>
<source>Choose the default subdivision unit to show in the interface and when sending coins.</source>
<translation>Valitse mitä yksikköä käytetään ensisijaisesti academiccoin-määrien näyttämiseen.</translation>
</message>
<message>
<location line="+9"/>
<source>Whether to show Academiccoin addresses in the transaction list or not.</source>
<translation>Näytetäänkö Academiccoin-osoitteet rahansiirrot listassa vai ei.</translation>
</message>
<message>
<location line="+3"/>
<source>&Display addresses in transaction list</source>
<translation>&Näytä osoitteet rahansiirrot listassa</translation>
</message>
<message>
<location line="+71"/>
<source>&OK</source>
<translation>&OK</translation>
</message>
<message>
<location line="+7"/>
<source>&Cancel</source>
<translation>&Peruuta</translation>
</message>
<message>
<location line="+10"/>
<source>&Apply</source>
<translation>&Hyväksy</translation>
</message>
<message>
<location filename="../optionsdialog.cpp" line="+53"/>
<source>default</source>
<translation>oletus</translation>
</message>
<message>
<location line="+130"/>
<source>Confirm options reset</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Some settings may require a client restart to take effect.</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+0"/>
<source>Do you want to proceed?</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+42"/>
<location line="+9"/>
<source>Warning</source>
<translation>Varoitus</translation>
</message>
<message>
<location line="-9"/>
<location line="+9"/>
<source>This setting will take effect after restarting Academiccoin.</source>
<translation>Tämä asetus astuu voimaan seuraavalla kerralla, kun Academiccoin käynnistetään.</translation>
</message>
<message>
<location line="+29"/>
<source>The supplied proxy address is invalid.</source>
<translation>Antamasi proxy-osoite on virheellinen.</translation>
</message>
</context>
<context>
<name>OverviewPage</name>
<message>
<location filename="../forms/overviewpage.ui" line="+14"/>
<source>Form</source>
<translation>Lomake</translation>
</message>
<message>
<location line="+50"/>
<location line="+166"/>
<source>The displayed information may be out of date. Your wallet automatically synchronizes with the Academiccoin network after a connection is established, but this process has not completed yet.</source>
<translation>Näytetyt tiedot eivät välttämättä ole ajantasalla. Lompakkosi synkronoituu Academiccoin-verkon kanssa automaattisesti yhteyden muodostamisen jälkeen, mutta synkronointi on vielä meneillään.</translation>
</message>
<message>
<location line="-124"/>
<source>Balance:</source>
<translation>Saldo:</translation>
</message>
<message>
<location line="+29"/>
<source>Unconfirmed:</source>
<translation>Vahvistamatta:</translation>
</message>
<message>
<location line="-78"/>
<source>Wallet</source>
<translation>Lompakko</translation>
</message>
<message>
<location line="+107"/>
<source>Immature:</source>
<translation>Epäkypsää:</translation>
</message>
<message>
<location line="+13"/>
<source>Mined balance that has not yet matured</source>
<translation>Louhittu saldo, joka ei ole vielä kypsynyt</translation>
</message>
<message>
<location line="+46"/>
<source><b>Recent transactions</b></source>
<translation><b>Viimeisimmät rahansiirrot</b></translation>
</message>
<message>
<location line="-101"/>
<source>Your current balance</source>
<translation>Tililläsi tällä hetkellä olevien Academiccoinien määrä</translation>
</message>
<message>
<location line="+29"/>
<source>Total of transactions that have yet to be confirmed, and do not yet count toward the current balance</source>
<translation>Niiden saapuvien rahansiirtojen määrä, joita Academiccoin-verkko ei vielä ole ehtinyt vahvistaa ja siten eivät vielä näy saldossa.</translation>
</message>
<message>
<location filename="../overviewpage.cpp" line="+116"/>
<location line="+1"/>
<source>out of sync</source>
<translation>Ei ajan tasalla</translation>
</message>
</context>
<context>
<name>PaymentServer</name>
<message>
<location filename="../paymentserver.cpp" line="+107"/>
<source>Cannot start academiccoin: click-to-pay handler</source>
<translation type="unfinished"/>
</message>
</context>
<context>
<name>QRCodeDialog</name>
<message>
<location filename="../forms/qrcodedialog.ui" line="+14"/>
<source>QR Code Dialog</source>
<translation>QR-koodi Dialogi</translation>
</message>
<message>
<location line="+59"/>
<source>Request Payment</source>
<translation>Vastaanota maksu</translation>
</message>
<message>
<location line="+56"/>
<source>Amount:</source>
<translation>Määrä:</translation>
</message>
<message>
<location line="-44"/>
<source>Label:</source>
<translation>Tunniste:</translation>
</message>
<message>
<location line="+19"/>
<source>Message:</source>
<translation>Viesti:</translation>
</message>
<message>
<location line="+71"/>
<source>&Save As...</source>
<translation>&Tallenna nimellä...</translation>
</message>
<message>
<location filename="../qrcodedialog.cpp" line="+62"/>
<source>Error encoding URI into QR Code.</source>
<translation>Virhe käännettäessä URI:a QR-koodiksi.</translation>
</message>
<message>
<location line="+40"/>
<source>The entered amount is invalid, please check.</source>
<translation>Syötetty määrä on virheellinen. Tarkista kirjoitusasu.</translation>
</message>
<message>
<location line="+23"/>
<source>Resulting URI too long, try to reduce the text for label / message.</source>
<translation>Tuloksen URI liian pitkä, yritä lyhentää otsikon tekstiä / viestiä.</translation>
</message>
<message>
<location line="+25"/>
<source>Save QR Code</source>
<translation>Tallenna QR-koodi</translation>
</message>
<message>
<location line="+0"/>
<source>PNG Images (*.png)</source>
<translation>PNG kuvat (*png)</translation>
</message>
</context>
<context>
<name>RPCConsole</name>
<message>
<location filename="../forms/rpcconsole.ui" line="+46"/>
<source>Client name</source>
<translation>Pääteohjelman nimi</translation>
</message>
<message>
<location line="+10"/>
<location line="+23"/>
<location line="+26"/>
<location line="+23"/>
<location line="+23"/>
<location line="+36"/>
<location line="+53"/>
<location line="+23"/>
<location line="+23"/>
<location filename="../rpcconsole.cpp" line="+339"/>
<source>N/A</source>
<translation>Ei saatavilla</translation>
</message>
<message>
<location line="-217"/>
<source>Client version</source>
<translation>Pääteohjelman versio</translation>
</message>
<message>
<location line="-45"/>
<source>&Information</source>
<translation>T&ietoa</translation>
</message>
<message>
<location line="+68"/>
<source>Using OpenSSL version</source>
<translation>Käytössä oleva OpenSSL-versio</translation>
</message>
<message>
<location line="+49"/>
<source>Startup time</source>
<translation>Käynnistysaika</translation>
</message>
<message>
<location line="+29"/>
<source>Network</source>
<translation>Verkko</translation>
</message>
<message>
<location line="+7"/>
<source>Number of connections</source>
<translation>Yhteyksien lukumäärä</translation>
</message>
<message>
<location line="+23"/>
<source>On testnet</source>
<translation>Käyttää testiverkkoa</translation>
</message>
<message>
<location line="+23"/>
<source>Block chain</source>
<translation>Lohkoketju</translation>
</message>
<message>
<location line="+7"/>
<source>Current number of blocks</source>
<translation>Nykyinen Lohkojen määrä</translation>
</message>
<message>
<location line="+23"/>
<source>Estimated total blocks</source>
<translation>Arvioitu lohkojen kokonaismäärä</translation>
</message>
<message>
<location line="+23"/>
<source>Last block time</source>
<translation>Viimeisimmän lohkon aika</translation>
</message>
<message>
<location line="+52"/>
<source>&Open</source>
<translation>&Avaa</translation>
</message>
<message>
<location line="+16"/>
<source>Command-line options</source>
<translation>Komentorivi parametrit</translation>
</message>
<message>
<location line="+7"/>
<source>Show the Academiccoin-Qt help message to get a list with possible Academiccoin command-line options.</source>
<translation>Näytä Academiccoin-Qt komentoriviparametrien ohjesivu, jossa on listattuna mahdolliset komentoriviparametrit.</translation>
</message>
<message>
<location line="+3"/>
<source>&Show</source>
<translation>&Näytä</translation>
</message>
<message>
<location line="+24"/>
<source>&Console</source>
<translation>&Konsoli</translation>
</message>
<message>
<location line="-260"/>
<source>Build date</source>
<translation>Kääntöpäiväys</translation>
</message>
<message>
<location line="-104"/>
<source>Academiccoin - Debug window</source>
<translation>Academiccoin - Debug ikkuna</translation>
</message>
<message>
<location line="+25"/>
<source>Academiccoin Core</source>
<translation>Academiccoin-ydin</translation>
</message>
<message>
<location line="+279"/>
<source>Debug log file</source>
<translation>Debug lokitiedosto</translation>
</message>
<message>
<location line="+7"/>
<source>Open the Academiccoin debug log file from the current data directory. This can take a few seconds for large log files.</source>
<translation>Avaa lokitiedosto nykyisestä data-kansiosta. Tämä voi viedä useamman sekunnin, jos lokitiedosto on iso.</translation>
</message>
<message>
<location line="+102"/>
<source>Clear console</source>
<translation>Tyhjennä konsoli</translation>
</message>
<message>
<location filename="../rpcconsole.cpp" line="-30"/>
<source>Welcome to the Academiccoin RPC console.</source>
<translation>Tervetuloa Academiccoin RPC konsoliin.</translation>
</message>
<message>
<location line="+1"/>
<source>Use up and down arrows to navigate history, and <b>Ctrl-L</b> to clear screen.</source>
<translation>Ylös- ja alas-nuolet selaavat historiaa ja <b>Ctrl-L</b> tyhjentää ruudun.</translation>
</message>
<message>
<location line="+1"/>
<source>Type <b>help</b> for an overview of available commands.</source>
<translation>Kirjoita <b>help</b> nähdäksesi yleiskatsauksen käytettävissä olevista komennoista.</translation>
</message>
</context>
<context>
<name>SendCoinsDialog</name>
<message>
<location filename="../forms/sendcoinsdialog.ui" line="+14"/>
<location filename="../sendcoinsdialog.cpp" line="+124"/>
<location line="+5"/>
<location line="+5"/>
<location line="+5"/>
<location line="+6"/>
<location line="+5"/>
<location line="+5"/>
<source>Send Coins</source>
<translation>Lähetä Academiccoineja</translation>
</message>
<message>
<location line="+50"/>
<source>Send to multiple recipients at once</source>
<translation>Lähetä monelle vastaanottajalle</translation>
</message>
<message>
<location line="+3"/>
<source>Add &Recipient</source>
<translation>Lisää &Vastaanottaja</translation>
</message>
<message>
<location line="+20"/>
<source>Remove all transaction fields</source>
<translation>Poista kaikki rahansiirtokentät</translation>
</message>
<message>
<location line="+3"/>
<source>Clear &All</source>
<translation>&Tyhjennnä Kaikki</translation>
</message>
<message>
<location line="+22"/>
<source>Balance:</source>
<translation>Saldo:</translation>
</message>
<message>
<location line="+10"/>
<source>123.456 ACC</source>
<translation>123,456 ACC</translation>
</message>
<message>
<location line="+31"/>
<source>Confirm the send action</source>
<translation>Vahvista lähetys</translation>
</message>
<message>
<location line="+3"/>
<source>S&end</source>
<translation>&Lähetä</translation>
</message>
<message>
<location filename="../sendcoinsdialog.cpp" line="-59"/>
<source><b>%1</b> to %2 (%3)</source>
<translation><b>%1</b> to %2 (%3)</translation>
</message>
<message>
<location line="+5"/>
<source>Confirm send coins</source>
<translation>Hyväksy Academiccoinien lähettäminen</translation>
</message>
<message>
<location line="+1"/>
<source>Are you sure you want to send %1?</source>
<translation>Haluatko varmasti lähettää %1?</translation>
</message>
<message>
<location line="+0"/>
<source> and </source>
<translation> ja </translation>
</message>
<message>
<location line="+23"/>
<source>The recipient address is not valid, please recheck.</source>
<translation>Vastaanottajan osoite on virheellinen. Tarkista osoite.</translation>
</message>
<message>
<location line="+5"/>
<source>The amount to pay must be larger than 0.</source>
<translation>Maksettavan summan tulee olla suurempi kuin 0 Academiccoinia.</translation>
</message>
<message>
<location line="+5"/>
<source>The amount exceeds your balance.</source>
<translation>Määrä ylittää käytettävissä olevan saldon.</translation>
</message>
<message>
<location line="+5"/>
<source>The total exceeds your balance when the %1 transaction fee is included.</source>
<translation>Kokonaismäärä ylittää saldosi kun %1 maksukulu lisätään summaan.</translation>
</message>
<message>
<location line="+6"/>
<source>Duplicate address found, can only send to each address once per send operation.</source>
<translation>Sama osoite toistuu useamman kerran. Samaan osoitteeseen voi lähettää vain kerran per maksu.</translation>
</message>
<message>
<location line="+5"/>
<source>Error: Transaction creation failed!</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+5"/>
<source>Error: The transaction was rejected. This might happen if some of the coins in your wallet were already spent, such as if you used a copy of wallet.dat and coins were spent in the copy but not marked as spent here.</source>
<translation>Virhe: Rahansiirto hylättiin. Tämä voi tapahtua jos jotkin academiccoineistasi on jo käytetty, esimerkiksi jos olet käyttänyt kopiota wallet.dat-lompakkotiedostosta ja academiccoinit on merkitty käytetyksi vain kopiossa.</translation>
</message>
</context>
<context>
<name>SendCoinsEntry</name>
<message>
<location filename="../forms/sendcoinsentry.ui" line="+14"/>
<source>Form</source>
<translation>Lomake</translation>
</message>
<message>
<location line="+15"/>
<source>A&mount:</source>
<translation>M&äärä:</translation>
</message>
<message>
<location line="+13"/>
<source>Pay &To:</source>
<translation>Maksun saaja:</translation>
</message>
<message>
<location line="+34"/>
<source>The address to send the payment to (e.g. 1NS17iag9jJgTHD1VXjvLCEnZuQ3rJDE9L)</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+60"/>
<location filename="../sendcoinsentry.cpp" line="+26"/>
<source>Enter a label for this address to add it to your address book</source>
<translation>Anna nimi tälle osoitteelle, jos haluat lisätä sen osoitekirjaan</translation>
</message>
<message>
<location line="-78"/>
<source>&Label:</source>
<translation>&Nimi:</translation>
</message>
<message>
<location line="+28"/>
<source>Choose address from address book</source>
<translation>Valitse osoite osoitekirjasta</translation>
</message>
<message>
<location line="+10"/>
<source>Alt+A</source>
<translation>Alt+A</translation>
</message>
<message>
<location line="+7"/>
<source>Paste address from clipboard</source>
<translation>Liitä osoite leikepöydältä</translation>
</message>
<message>
<location line="+10"/>
<source>Alt+P</source>
<translation>Alt+P</translation>
</message>
<message>
<location line="+7"/>
<source>Remove this recipient</source>
<translation>Poista </translation>
</message>
<message>
<location filename="../sendcoinsentry.cpp" line="+1"/>
<source>Enter a Academiccoin address (e.g. 1NS17iag9jJgTHD1VXjvLCEnZuQ3rJDE9L)</source>
<translation>Anna Academiccoin-osoite (esim. 1NS17iag9jJgTHD1VXjvLCEnZuQ3rJDE9L)</translation>
</message>
</context>
<context>
<name>SignVerifyMessageDialog</name>
<message>
<location filename="../forms/signverifymessagedialog.ui" line="+14"/>
<source>Signatures - Sign / Verify a Message</source>
<translation>Allekirjoitukset - Allekirjoita / Varmista viesti</translation>
</message>
<message>
<location line="+13"/>
<source>&Sign Message</source>
<translation>&Allekirjoita viesti</translation>
</message>
<message>
<location line="+6"/>
<source>You can sign messages with your addresses to prove you own them. Be careful not to sign anything vague, as phishing attacks may try to trick you into signing your identity over to them. Only sign fully-detailed statements you agree to.</source>
<translation>Voit allekirjoittaa viestit omalla osoitteellasi todistaaksesi että omistat ne. Ole huolellinen, että et allekirjoita mitään epämääräistä, phishing-hyökkääjät voivat huijata sinua allekirjoittamaan luovuttamalla henkilöllisyytesi. Allekirjoita selvitys täysin yksityiskohtaisesti mihin olet sitoutunut.</translation>
</message>
<message>
<location line="+18"/>
<source>The address to sign the message with (e.g. 1NS17iag9jJgTHD1VXjvLCEnZuQ3rJDE9L)</source>
<translation>Osoite, jolla viesti allekirjoitetaan (esimerkiksi 1NS17iag9jJgTHD1VXjvLCEnZuQ3rJDE9L)</translation>
</message>
<message>
<location line="+10"/>
<location line="+213"/>
<source>Choose an address from the address book</source>
<translation>Valitse osoite osoitekirjasta</translation>
</message>
<message>
<location line="-203"/>
<location line="+213"/>
<source>Alt+A</source>
<translation>Alt+A</translation>
</message>
<message>
<location line="-203"/>
<source>Paste address from clipboard</source>
<translation>Liitä osoite leikepöydältä</translation>
</message>
<message>
<location line="+10"/>
<source>Alt+P</source>
<translation>Alt+P</translation>
</message>
<message>
<location line="+12"/>
<source>Enter the message you want to sign here</source>
<translation>Kirjoita tähän viesti minkä haluat allekirjoittaa</translation>
</message>
<message>
<location line="+7"/>
<source>Signature</source>
<translation>Allekirjoitus</translation>
</message>
<message>
<location line="+27"/>
<source>Copy the current signature to the system clipboard</source>
<translation>Kopioi tämänhetkinen allekirjoitus leikepöydälle</translation>
</message>
<message>
<location line="+21"/>
<source>Sign the message to prove you own this Academiccoin address</source>
<translation>Allekirjoita viesti todistaaksesi, että omistat tämän Academiccoin-osoitteen</translation>
</message>
<message>
<location line="+3"/>
<source>Sign &Message</source>
<translation>Allekirjoita &viesti</translation>
</message>
<message>
<location line="+14"/>
<source>Reset all sign message fields</source>
<translation>Tyhjennä kaikki allekirjoita-viesti-kentät</translation>
</message>
<message>
<location line="+3"/>
<location line="+146"/>
<source>Clear &All</source>
<translation>&Tyhjennä Kaikki</translation>
</message>
<message>
<location line="-87"/>
<source>&Verify Message</source>
<translation>&Varmista viesti</translation>
</message>
<message>
<location line="+6"/>
<source>Enter the signing address, message (ensure you copy line breaks, spaces, tabs, etc. exactly) and signature below to verify the message. Be careful not to read more into the signature than what is in the signed message itself, to avoid being tricked by a man-in-the-middle attack.</source>
<translation>Syötä allekirjoittava osoite, viesti ja allekirjoitus alla oleviin kenttiin varmistaaksesi allekirjoituksen aitouden. Varmista että kopioit kaikki kentät täsmälleen oikein, myös rivinvaihdot, välilyönnit, tabulaattorit, jne.</translation>
</message>
<message>
<location line="+21"/>
<source>The address the message was signed with (e.g. 1NS17iag9jJgTHD1VXjvLCEnZuQ3rJDE9L)</source>
<translation>Osoite, jolla viesti allekirjoitettiin (esimerkiksi 1NS17iag9jJgTHD1VXjvLCEnZuQ3rJDE9L)</translation>
</message>
<message>
<location line="+40"/>
<source>Verify the message to ensure it was signed with the specified Academiccoin address</source>
<translation>Tarkista viestin allekirjoitus varmistaaksesi, että se allekirjoitettiin tietyllä Academiccoin-osoitteella</translation>
</message>
<message>
<location line="+3"/>
<source>Verify &Message</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+14"/>
<source>Reset all verify message fields</source>
<translation>Tyhjennä kaikki varmista-viesti-kentät</translation>
</message>
<message>
<location filename="../signverifymessagedialog.cpp" line="+27"/>
<location line="+3"/>
<source>Enter a Academiccoin address (e.g. 1NS17iag9jJgTHD1VXjvLCEnZuQ3rJDE9L)</source>
<translation>Anna Academiccoin-osoite (esim. 1NS17iag9jJgTHD1VXjvLCEnZuQ3rJDE9L)</translation>
</message>
<message>
<location line="-2"/>
<source>Click "Sign Message" to generate signature</source>
<translation>Klikkaa "Allekirjoita Viesti luodaksesi allekirjoituksen </translation>
</message>
<message>
<location line="+3"/>
<source>Enter Academiccoin signature</source>
<translation>Syötä Academiccoin-allekirjoitus</translation>
</message>
<message>
<location line="+82"/>
<location line="+81"/>
<source>The entered address is invalid.</source>
<translation>Syötetty osoite on virheellinen.</translation>
</message>
<message>
<location line="-81"/>
<location line="+8"/>
<location line="+73"/>
<location line="+8"/>
<source>Please check the address and try again.</source>
<translation>Tarkista osoite ja yritä uudelleen.</translation>
</message>
<message>
<location line="-81"/>
<location line="+81"/>
<source>The entered address does not refer to a key.</source>
<translation>Syötetyn osoitteen avainta ei löydy.</translation>
</message>
<message>
<location line="-73"/>
<source>Wallet unlock was cancelled.</source>
<translation>Lompakon avaaminen peruttiin.</translation>
</message>
<message>
<location line="+8"/>
<source>Private key for the entered address is not available.</source>
<translation>Yksityistä avainta syötetylle osoitteelle ei ole saatavilla.</translation>
</message>
<message>
<location line="+12"/>
<source>Message signing failed.</source>
<translation>Viestin allekirjoitus epäonnistui.</translation>
</message>
<message>
<location line="+5"/>
<source>Message signed.</source>
<translation>Viesti allekirjoitettu.</translation>
</message>
<message>
<location line="+59"/>
<source>The signature could not be decoded.</source>
<translation>Allekirjoitusta ei pystytty tulkitsemaan.</translation>
</message>
<message>
<location line="+0"/>
<location line="+13"/>
<source>Please check the signature and try again.</source>
<translation>Tarkista allekirjoitus ja yritä uudelleen.</translation>
</message>
<message>
<location line="+0"/>
<source>The signature did not match the message digest.</source>
<translation>Allekirjoitus ei täsmää viestin tiivisteeseen.</translation>
</message>
<message>
<location line="+7"/>
<source>Message verification failed.</source>
<translation>Viestin varmistus epäonnistui.</translation>
</message>
<message>
<location line="+5"/>
<source>Message verified.</source>
<translation>Viesti varmistettu.</translation>
</message>
</context>
<context>
<name>SplashScreen</name>
<message>
<location filename="../splashscreen.cpp" line="+22"/>
<source>The Academiccoin developers</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>[testnet]</source>
<translation>[testnet]</translation>
</message>
</context>
<context>
<name>TransactionDesc</name>
<message>
<location filename="../transactiondesc.cpp" line="+20"/>
<source>Open until %1</source>
<translation>Avoinna %1 asti</translation>
</message>
<message>
<location line="+6"/>
<source>%1/offline</source>
<translation>%1/offline</translation>
</message>
<message>
<location line="+2"/>
<source>%1/unconfirmed</source>
<translation>%1/vahvistamaton</translation>
</message>
<message>
<location line="+2"/>
<source>%1 confirmations</source>
<translation>%1 vahvistusta</translation>
</message>
<message>
<location line="+18"/>
<source>Status</source>
<translation>Tila</translation>
</message>
<message numerus="yes">
<location line="+7"/>
<source>, broadcast through %n node(s)</source>
<translation><numerusform>lähetetty %n noodin läpi</numerusform><numerusform>lähetetty %n noodin läpi</numerusform></translation>
</message>
<message>
<location line="+4"/>
<source>Date</source>
<translation>Päivämäärä</translation>
</message>
<message>
<location line="+7"/>
<source>Source</source>
<translation>Lähde</translation>
</message>
<message>
<location line="+0"/>
<source>Generated</source>
<translation>Generoitu</translation>
</message>
<message>
<location line="+5"/>
<location line="+17"/>
<source>From</source>
<translation>Lähettäjä</translation>
</message>
<message>
<location line="+1"/>
<location line="+22"/>
<location line="+58"/>
<source>To</source>
<translation>Saaja</translation>
</message>
<message>
<location line="-77"/>
<location line="+2"/>
<source>own address</source>
<translation>oma osoite</translation>
</message>
<message>
<location line="-2"/>
<source>label</source>
<translation>nimi</translation>
</message>
<message>
<location line="+37"/>
<location line="+12"/>
<location line="+45"/>
<location line="+17"/>
<location line="+30"/>
<source>Credit</source>
<translation>Credit</translation>
</message>
<message numerus="yes">
<location line="-102"/>
<source>matures in %n more block(s)</source>
<translation><numerusform>kypsyy %n lohkon kuluttua</numerusform><numerusform>kypsyy %n lohkon kuluttua</numerusform></translation>
</message>
<message>
<location line="+2"/>
<source>not accepted</source>
<translation>ei hyväksytty</translation>
</message>
<message>
<location line="+44"/>
<location line="+8"/>
<location line="+15"/>
<location line="+30"/>
<source>Debit</source>
<translation>Debit</translation>
</message>
<message>
<location line="-39"/>
<source>Transaction fee</source>
<translation>Maksukulu</translation>
</message>
<message>
<location line="+16"/>
<source>Net amount</source>
<translation>Netto määrä</translation>
</message>
<message>
<location line="+6"/>
<source>Message</source>
<translation>Viesti</translation>
</message>
<message>
<location line="+2"/>
<source>Comment</source>
<translation>Viesti</translation>
</message>
<message>
<location line="+2"/>
<source>Transaction ID</source>
<translation>Siirtotunnus</translation>
</message>
<message>
<location line="+3"/>
<source>Generated coins must mature 120 blocks before they can be spent. When you generated this block, it was broadcast to the network to be added to the block chain. If it fails to get into the chain, its state will change to "not accepted" and it won't be spendable. This may occasionally happen if another node generates a block within a few seconds of yours.</source>
<translation>Generoitujen kolikoiden täytyy kypsyä 120 lohkon ajan ennen kuin ne voidaan lähettää. Kun loit tämän lohkon, se lähetettiin verkkoon lisättäväksi lohkoketjuun. Jos se ei päädy osaksi lohkoketjua, sen tila vaihtuu "ei hyväksytty" ja sitä ei voida lähettää. Näin voi joskus käydä, jos toinen noodi löytää lohkon muutamaa sekuntia ennen tai jälkeen sinun lohkosi löytymisen.</translation>
</message>
<message>
<location line="+7"/>
<source>Debug information</source>
<translation>Debug tiedot</translation>
</message>
<message>
<location line="+8"/>
<source>Transaction</source>
<translation>Rahansiirto</translation>
</message>
<message>
<location line="+3"/>
<source>Inputs</source>
<translation>Sisääntulot</translation>
</message>
<message>
<location line="+23"/>
<source>Amount</source>
<translation>Määrä</translation>
</message>
<message>
<location line="+1"/>
<source>true</source>
<translation>tosi</translation>
</message>
<message>
<location line="+0"/>
<source>false</source>
<translation>epätosi</translation>
</message>
<message>
<location line="-209"/>
<source>, has not been successfully broadcast yet</source>
<translation>, ei ole vielä onnistuneesti lähetetty</translation>
</message>
<message numerus="yes">
<location line="-35"/>
<source>Open for %n more block(s)</source>
<translation type="unfinished"><numerusform></numerusform><numerusform></numerusform></translation>
</message>
<message>
<location line="+70"/>
<source>unknown</source>
<translation>tuntematon</translation>
</message>
</context>
<context>
<name>TransactionDescDialog</name>
<message>
<location filename="../forms/transactiondescdialog.ui" line="+14"/>
<source>Transaction details</source>
<translation>Rahansiirron yksityiskohdat</translation>
</message>
<message>
<location line="+6"/>
<source>This pane shows a detailed description of the transaction</source>
<translation>Tämä ruutu näyttää yksityiskohtaisen tiedon rahansiirrosta</translation>
</message>
</context>
<context>
<name>TransactionTableModel</name>
<message>
<location filename="../transactiontablemodel.cpp" line="+225"/>
<source>Date</source>
<translation>Päivämäärä</translation>
</message>
<message>
<location line="+0"/>
<source>Type</source>
<translation>Laatu</translation>
</message>
<message>
<location line="+0"/>
<source>Address</source>
<translation>Osoite</translation>
</message>
<message>
<location line="+0"/>
<source>Amount</source>
<translation>Määrä</translation>
</message>
<message numerus="yes">
<location line="+57"/>
<source>Open for %n more block(s)</source>
<translation type="unfinished"><numerusform></numerusform><numerusform></numerusform></translation>
</message>
<message>
<location line="+3"/>
<source>Open until %1</source>
<translation>Avoinna %1 asti</translation>
</message>
<message>
<location line="+3"/>
<source>Offline (%1 confirmations)</source>
<translation>Ei yhteyttä verkkoon (%1 vahvistusta)</translation>
</message>
<message>
<location line="+3"/>
<source>Unconfirmed (%1 of %2 confirmations)</source>
<translation>Vahvistamatta (%1/%2 vahvistusta)</translation>
</message>
<message>
<location line="+3"/>
<source>Confirmed (%1 confirmations)</source>
<translation>Vahvistettu (%1 vahvistusta)</translation>
</message>
<message numerus="yes">
<location line="+8"/>
<source>Mined balance will be available when it matures in %n more block(s)</source>
<translation><numerusform>Louhittu saldo on käytettävissä kun se kypsyy %n lohkon päästä</numerusform><numerusform>Louhittu saldo on käytettävissä kun se kypsyy %n lohkon päästä</numerusform></translation>
</message>
<message>
<location line="+5"/>
<source>This block was not received by any other nodes and will probably not be accepted!</source>
<translation>Tätä lohkoa ei vastaanotettu mistään muusta solmusta ja sitä ei mahdollisesti hyväksytä!</translation>
</message>
<message>
<location line="+3"/>
<source>Generated but not accepted</source>
<translation>Generoitu mutta ei hyväksytty</translation>
</message>
<message>
<location line="+43"/>
<source>Received with</source>
<translation>Vastaanotettu osoitteella</translation>
</message>
<message>
<location line="+2"/>
<source>Received from</source>
<translation>Vastaanotettu</translation>
</message>
<message>
<location line="+3"/>
<source>Sent to</source>
<translation>Saaja</translation>
</message>
<message>
<location line="+2"/>
<source>Payment to yourself</source>
<translation>Maksu itsellesi</translation>
</message>
<message>
<location line="+2"/>
<source>Mined</source>
<translation>Louhittu</translation>
</message>
<message>
<location line="+38"/>
<source>(n/a)</source>
<translation>(ei saatavilla)</translation>
</message>
<message>
<location line="+199"/>
<source>Transaction status. Hover over this field to show number of confirmations.</source>
<translation>Rahansiirron tila. Siirrä osoitin kentän päälle nähdäksesi vahvistusten lukumäärä.</translation>
</message>
<message>
<location line="+2"/>
<source>Date and time that the transaction was received.</source>
<translation>Rahansiirron vastaanottamisen päivämäärä ja aika.</translation>
</message>
<message>
<location line="+2"/>
<source>Type of transaction.</source>
<translation>Rahansiirron laatu.</translation>
</message>
<message>
<location line="+2"/>
<source>Destination address of transaction.</source>
<translation>Rahansiirron kohteen Academiccoin-osoite</translation>
</message>
<message>
<location line="+2"/>
<source>Amount removed from or added to balance.</source>
<translation>Saldoon lisätty tai siitä vähennetty määrä.</translation>
</message>
</context>
<context>
<name>TransactionView</name>
<message>
<location filename="../transactionview.cpp" line="+52"/>
<location line="+16"/>
<source>All</source>
<translation>Kaikki</translation>
</message>
<message>
<location line="-15"/>
<source>Today</source>
<translation>Tänään</translation>
</message>
<message>
<location line="+1"/>
<source>This week</source>
<translation>Tällä viikolla</translation>
</message>
<message>
<location line="+1"/>
<source>This month</source>
<translation>Tässä kuussa</translation>
</message>
<message>
<location line="+1"/>
<source>Last month</source>
<translation>Viime kuussa</translation>
</message>
<message>
<location line="+1"/>
<source>This year</source>
<translation>Tänä vuonna</translation>
</message>
<message>
<location line="+1"/>
<source>Range...</source>
<translation>Alue...</translation>
</message>
<message>
<location line="+11"/>
<source>Received with</source>
<translation>Vastaanotettu osoitteella</translation>
</message>
<message>
<location line="+2"/>
<source>Sent to</source>
<translation>Saaja</translation>
</message>
<message>
<location line="+2"/>
<source>To yourself</source>
<translation>Itsellesi</translation>
</message>
<message>
<location line="+1"/>
<source>Mined</source>
<translation>Louhittu</translation>
</message>
<message>
<location line="+1"/>
<source>Other</source>
<translation>Muu</translation>
</message>
<message>
<location line="+7"/>
<source>Enter address or label to search</source>
<translation>Anna etsittävä osoite tai tunniste</translation>
</message>
<message>
<location line="+7"/>
<source>Min amount</source>
<translation>Minimimäärä</translation>
</message>
<message>
<location line="+34"/>
<source>Copy address</source>
<translation>Kopioi osoite</translation>
</message>
<message>
<location line="+1"/>
<source>Copy label</source>
<translation>Kopioi nimi</translation>
</message>
<message>
<location line="+1"/>
<source>Copy amount</source>
<translation>Kopioi määrä</translation>
</message>
<message>
<location line="+1"/>
<source>Copy transaction ID</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Edit label</source>
<translation>Muokkaa nimeä</translation>
</message>
<message>
<location line="+1"/>
<source>Show transaction details</source>
<translation>Näytä rahansiirron yksityiskohdat</translation>
</message>
<message>
<location line="+139"/>
<source>Export Transaction Data</source>
<translation>Vie rahansiirron tiedot</translation>
</message>
<message>
<location line="+1"/>
<source>Comma separated file (*.csv)</source>
<translation>Comma separated file (*.csv)</translation>
</message>
<message>
<location line="+8"/>
<source>Confirmed</source>
<translation>Vahvistettu</translation>
</message>
<message>
<location line="+1"/>
<source>Date</source>
<translation>Aika</translation>
</message>
<message>
<location line="+1"/>
<source>Type</source>
<translation>Laatu</translation>
</message>
<message>
<location line="+1"/>
<source>Label</source>
<translation>Nimi</translation>
</message>
<message>
<location line="+1"/>
<source>Address</source>
<translation>Osoite</translation>
</message>
<message>
<location line="+1"/>
<source>Amount</source>
<translation>Määrä</translation>
</message>
<message>
<location line="+1"/>
<source>ID</source>
<translation>ID</translation>
</message>
<message>
<location line="+4"/>
<source>Error exporting</source>
<translation>Virhe tietojen viennissä</translation>
</message>
<message>
<location line="+0"/>
<source>Could not write to file %1.</source>
<translation>Ei voida kirjoittaa tiedostoon %1.</translation>
</message>
<message>
<location line="+100"/>
<source>Range:</source>
<translation>Alue:</translation>
</message>
<message>
<location line="+8"/>
<source>to</source>
<translation>kenelle</translation>
</message>
</context>
<context>
<name>WalletModel</name>
<message>
<location filename="../walletmodel.cpp" line="+193"/>
<source>Send Coins</source>
<translation>Lähetä Academiccoineja</translation>
</message>
</context>
<context>
<name>WalletView</name>
<message>
<location filename="../walletview.cpp" line="+42"/>
<source>&Export</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Export the data in the current tab to a file</source>
<translation>Vie auki olevan välilehden tiedot tiedostoon</translation>
</message>
<message>
<location line="+193"/>
<source>Backup Wallet</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+0"/>
<source>Wallet Data (*.dat)</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+3"/>
<source>Backup Failed</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+0"/>
<source>There was an error trying to save the wallet data to the new location.</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+4"/>
<source>Backup Successful</source>
<translation>Varmuuskopio Onnistui</translation>
</message>
<message>
<location line="+0"/>
<source>The wallet data was successfully saved to the new location.</source>
<translation type="unfinished"/>
</message>
</context>
<context>
<name>academiccoin-core</name>
<message>
<location filename="../academiccoinstrings.cpp" line="+94"/>
<source>Academiccoin version</source>
<translation>Academiccoinin versio</translation>
</message>
<message>
<location line="+102"/>
<source>Usage:</source>
<translation>Käyttö:</translation>
</message>
<message>
<location line="-29"/>
<source>Send command to -server or academiccoind</source>
<translation>Lähetä käsky palvelimelle tai academiccoind:lle</translation>
</message>
<message>
<location line="-23"/>
<source>List commands</source>
<translation>Lista komennoista</translation>
</message>
<message>
<location line="-12"/>
<source>Get help for a command</source>
<translation>Hanki apua käskyyn</translation>
</message>
<message>
<location line="+24"/>
<source>Options:</source>
<translation>Asetukset:</translation>
</message>
<message>
<location line="+24"/>
<source>Specify configuration file (default: academiccoin.conf)</source>
<translation>Määritä asetustiedosto (oletus: academiccoin.conf)</translation>
</message>
<message>
<location line="+3"/>
<source>Specify pid file (default: academiccoind.pid)</source>
<translation>Määritä pid-tiedosto (oletus: academiccoin.pid)</translation>
</message>
<message>
<location line="-1"/>
<source>Specify data directory</source>
<translation>Määritä data-hakemisto</translation>
</message>
<message>
<location line="-9"/>
<source>Set database cache size in megabytes (default: 25)</source>
<translation>Aseta tietokannan välimuistin koko megatavuina (oletus: 25)</translation>
</message>
<message>
<location line="-28"/>
<source>Listen for connections on <port> (default: 9115 or testnet: 19115)</source>
<translation>Kuuntele yhteyksiä portista <port> (oletus: 9115 tai testnet: 19115)</translation>
</message>
<message>
<location line="+5"/>
<source>Maintain at most <n> connections to peers (default: 125)</source>
<translation>Pidä enintään <n> yhteyttä verkkoihin (oletus: 125)</translation>
</message>
<message>
<location line="-48"/>
<source>Connect to a node to retrieve peer addresses, and disconnect</source>
<translation>Yhdistä noodiin hakeaksesi naapurien osoitteet ja katkaise yhteys</translation>
</message>
<message>
<location line="+82"/>
<source>Specify your own public address</source>
<translation>Määritä julkinen osoitteesi</translation>
</message>
<message>
<location line="+3"/>
<source>Threshold for disconnecting misbehaving peers (default: 100)</source>
<translation>Kynnysarvo aikakatkaisulle heikosti toimiville verkoille (oletus: 100)</translation>
</message>
<message>
<location line="-134"/>
<source>Number of seconds to keep misbehaving peers from reconnecting (default: 86400)</source>
<translation>Sekuntien määrä, kuinka kauan uudelleenkytkeydytään verkkoihin (oletus: 86400)</translation>
</message>
<message>
<location line="-29"/>
<source>An error occurred while setting up the RPC port %u for listening on IPv4: %s</source>
<translation>Virhe valmisteltaessa RPC-portin %u avaamista kuunneltavaksi: %s</translation>
</message>
<message>
<location line="+27"/>
<source>Listen for JSON-RPC connections on <port> (default: 9114 or testnet: 19114)</source>
<translation>Kuuntele JSON-RPC -yhteyksiä portista <port> (oletus: 9114 or testnet: 19114)</translation>
</message>
<message>
<location line="+37"/>
<source>Accept command line and JSON-RPC commands</source>
<translation>Hyväksy merkkipohjaiset- ja JSON-RPC-käskyt</translation>
</message>
<message>
<location line="+76"/>
<source>Run in the background as a daemon and accept commands</source>
<translation>Aja taustalla daemonina ja hyväksy komennot</translation>
</message>
<message>
<location line="+37"/>
<source>Use the test network</source>
<translation>Käytä test -verkkoa</translation>
</message>
<message>
<location line="-112"/>
<source>Accept connections from outside (default: 1 if no -proxy or -connect)</source>
<translation>Hyväksy yhteyksiä ulkopuolelta (vakioasetus: 1 jos -proxy tai -connect ei määritelty)</translation>
</message>
<message>
<location line="-80"/>
<source>%s, you must set a rpcpassword in the configuration file:
%s
It is recommended you use the following random password:
rpcuser=academiccoinrpc
rpcpassword=%s
(you do not need to remember this password)
The username and password MUST NOT be the same.
If the file does not exist, create it with owner-readable-only file permissions.
It is also recommended to set alertnotify so you are notified of problems;
for example: alertnotify=echo %%s | mail -s "Academiccoin Alert" admin@foo.com
</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+17"/>
<source>An error occurred while setting up the RPC port %u for listening on IPv6, falling back to IPv4: %s</source>
<translation>Virhe ilmennyt asetettaessa RPC-porttia %u IPv6:n kuuntelemiseksi, palataan takaisin IPv4:ään %s</translation>
</message>
<message>
<location line="+3"/>
<source>Bind to given address and always listen on it. Use [host]:port notation for IPv6</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+3"/>
<source>Cannot obtain a lock on data directory %s. Academiccoin is probably already running.</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+3"/>
<source>Error: The transaction was rejected! This might happen if some of the coins in your wallet were already spent, such as if you used a copy of wallet.dat and coins were spent in the copy but not marked as spent here.</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+4"/>
<source>Error: This transaction requires a transaction fee of at least %s because of its amount, complexity, or use of recently received funds!</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+3"/>
<source>Execute command when a relevant alert is received (%s in cmd is replaced by message)</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+3"/>
<source>Execute command when a wallet transaction changes (%s in cmd is replaced by TxID)</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+11"/>
<source>Set maximum size of high-priority/low-fee transactions in bytes (default: 27000)</source>
<translation>Aseta suurin korkean prioriteetin / matalan palkkion siirron koko tavuissa (vakioasetus: 27000)</translation>
</message>
<message>
<location line="+6"/>
<source>This is a pre-release test build - use at your own risk - do not use for mining or merchant applications</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+5"/>
<source>Warning: -paytxfee is set very high! This is the transaction fee you will pay if you send a transaction.</source>
<translation>Varoitus: -paytxfee on asetettu erittäin korkeaksi! Tämä on maksukulu jonka tulet maksamaan kun lähetät siirron.</translation>
</message>
<message>
<location line="+3"/>
<source>Warning: Displayed transactions may not be correct! You may need to upgrade, or other nodes may need to upgrade.</source>
<translation>Varoitus: Näytetyt siirrot eivät välttämättä pidä paikkaansa! Sinun tai toisten noodien voi olla tarpeen asentaa päivitys.</translation>
</message>
<message>
<location line="+3"/>
<source>Warning: Please check that your computer's date and time are correct! If your clock is wrong Academiccoin will not work properly.</source>
<translation>Varoitus: Tarkista että tietokoneesi kellonaika ja päivämäärä ovat paikkansapitäviä! Academiccoin ei toimi oikein väärällä päivämäärällä ja/tai kellonajalla.</translation>
</message>
<message>
<location line="+3"/>
<source>Warning: error reading wallet.dat! All keys read correctly, but transaction data or address book entries might be missing or incorrect.</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+3"/>
<source>Warning: wallet.dat corrupt, data salvaged! Original wallet.dat saved as wallet.{timestamp}.bak in %s; if your balance or transactions are incorrect you should restore from a backup.</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+14"/>
<source>Attempt to recover private keys from a corrupt wallet.dat</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+2"/>
<source>Block creation options:</source>
<translation>Lohkon luonnin asetukset:</translation>
</message>
<message>
<location line="+5"/>
<source>Connect only to the specified node(s)</source>
<translation>Yhidstä ainoastaan määrättyihin noodeihin</translation>
</message>
<message>
<location line="+3"/>
<source>Corrupted block database detected</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Discover own IP address (default: 1 when listening and no -externalip)</source>
<translation>Hae oma IP osoite (vakioasetus: 1 kun kuuntelemassa ja ei -externalip)</translation>
</message>
<message>
<location line="+1"/>
<source>Do you want to rebuild the block database now?</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+2"/>
<source>Error initializing block database</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Error initializing wallet database environment %s!</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Error loading block database</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+4"/>
<source>Error opening block database</source>
<translation>Virhe avattaessa lohkoindeksiä</translation>
</message>
<message>
<location line="+2"/>
<source>Error: Disk space is low!</source>
<translation>Varoitus: Levytila on vähissä!</translation>
</message>
<message>
<location line="+1"/>
<source>Error: Wallet locked, unable to create transaction!</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Error: system error: </source>
<translation>Virhe: Järjestelmävirhe</translation>
</message>
<message>
<location line="+1"/>
<source>Failed to listen on any port. Use -listen=0 if you want this.</source>
<translation>Ei onnistuttu kuuntelemaan missään portissa. Käytä -listen=0 jos haluat tätä.</translation>
</message>
<message>
<location line="+1"/>
<source>Failed to read block info</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Failed to read block</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Failed to sync block index</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Failed to write block index</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Failed to write block info</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Failed to write block</source>
<translation>Lohkon kirjoitus epäonnistui</translation>
</message>
<message>
<location line="+1"/>
<source>Failed to write file info</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Failed to write to coin database</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Failed to write transaction index</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Failed to write undo data</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+2"/>
<source>Find peers using DNS lookup (default: 1 unless -connect)</source>
<translation>Hae naapureita DNS hauilla (vakioasetus: 1 paitsi jos -connect)</translation>
</message>
<message>
<location line="+1"/>
<source>Generate coins (default: 0)</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+2"/>
<source>How many blocks to check at startup (default: 288, 0 = all)</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>How thorough the block verification is (0-4, default: 3)</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+19"/>
<source>Not enough file descriptors available.</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+8"/>
<source>Rebuild block chain index from current blk000??.dat files</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+16"/>
<source>Set the number of threads to service RPC calls (default: 4)</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+26"/>
<source>Verifying blocks...</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Verifying wallet...</source>
<translation type="unfinished"/>
</message>
<message>
<location line="-69"/>
<source>Imports blocks from external blk000??.dat file</source>
<translation>Tuodaan lohkoja ulkoisesta blk000??.dat tiedostosta</translation>
</message>
<message>
<location line="-76"/>
<source>Set the number of script verification threads (up to 16, 0 = auto, <0 = leave that many cores free, default: 0)</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+77"/>
<source>Information</source>
<translation>Tietoa</translation>
</message>
<message>
<location line="+3"/>
<source>Invalid -tor address: '%s'</source>
<translation>Virheellinen -tor osoite '%s'</translation>
</message>
<message>
<location line="+1"/>
<source>Invalid amount for -minrelaytxfee=<amount>: '%s'</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Invalid amount for -mintxfee=<amount>: '%s'</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+8"/>
<source>Maintain a full transaction index (default: 0)</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+2"/>
<source>Maximum per-connection receive buffer, <n>*1000 bytes (default: 5000)</source>
<translation>Suurin vastaanottopuskuri yksittäiselle yhteydelle, <n>*1000 tavua (vakioasetus: 5000)</translation>
</message>
<message>
<location line="+1"/>
<source>Maximum per-connection send buffer, <n>*1000 bytes (default: 1000)</source>
<translation>Suurin lähetyspuskuri yksittäiselle yhteydelle, <n>*1000 tavua (vakioasetus: 1000)</translation>
</message>
<message>
<location line="+2"/>
<source>Only accept block chain matching built-in checkpoints (default: 1)</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Only connect to nodes in network <net> (IPv4, IPv6 or Tor)</source>
<translation>Yhdistä vain noodeihin verkossa <net> (IPv4, IPv6 tai Tor)</translation>
</message>
<message>
<location line="+2"/>
<source>Output extra debugging information. Implies all other -debug* options</source>
<translation>Tulosta enemmän debug tietoa. Aktivoi kaikki -debug* asetukset</translation>
</message>
<message>
<location line="+1"/>
<source>Output extra network debugging information</source>
<translation>Tulosta lisää verkkoyhteys debug tietoa</translation>
</message>
<message>
<location line="+2"/>
<source>Prepend debug output with timestamp</source>
<translation>Lisää debuggaustiedon tulostukseen aikaleima</translation>
</message>
<message>
<location line="+5"/>
<source>SSL options: (see the Academiccoin Wiki for SSL setup instructions)</source>
<translation>SSL asetukset (katso Academiccoin Wikistä tarkemmat SSL ohjeet)</translation>
</message>
<message>
<location line="+1"/>
<source>Select the version of socks proxy to use (4-5, default: 5)</source>
<translation>Valitse käytettävän SOCKS-proxyn versio (4-5, vakioasetus: 5)</translation>
</message>
<message>
<location line="+3"/>
<source>Send trace/debug info to console instead of debug.log file</source>
<translation>Lähetä jäljitys/debug-tieto konsoliin, debug.log-tiedoston sijaan</translation>
</message>
<message>
<location line="+1"/>
<source>Send trace/debug info to debugger</source>
<translation>Lähetä jäljitys/debug-tieto debuggeriin</translation>
</message>
<message>
<location line="+5"/>
<source>Set maximum block size in bytes (default: 250000)</source>
<translation>Aseta suurin lohkon koko tavuissa (vakioasetus: 250000)</translation>
</message>
<message>
<location line="+1"/>
<source>Set minimum block size in bytes (default: 0)</source>
<translation>Asetan pienin lohkon koko tavuissa (vakioasetus: 0)</translation>
</message>
<message>
<location line="+2"/>
<source>Shrink debug.log file on client startup (default: 1 when no -debug)</source>
<translation>Pienennä debug.log tiedosto käynnistyksen yhteydessä (vakioasetus: 1 kun ei -debug)</translation>
</message>
<message>
<location line="+1"/>
<source>Signing transaction failed</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+2"/>
<source>Specify connection timeout in milliseconds (default: 5000)</source>
<translation>Määritä yhteyden aikakataisu millisekunneissa (vakioasetus: 5000)</translation>
</message>
<message>
<location line="+4"/>
<source>System error: </source>
<translation>Järjestelmävirhe:</translation>
</message>
<message>
<location line="+4"/>
<source>Transaction amount too small</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Transaction amounts must be positive</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>Transaction too large</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+7"/>
<source>Use UPnP to map the listening port (default: 0)</source>
<translation>Käytä UPnP:tä kuunneltavan portin avaamiseen (vakioasetus: 0)</translation>
</message>
<message>
<location line="+1"/>
<source>Use UPnP to map the listening port (default: 1 when listening)</source>
<translation>Käytä UPnP:tä kuunneltavan portin avaamiseen (vakioasetus: 1 kun kuuntelemassa)</translation>
</message>
<message>
<location line="+1"/>
<source>Use proxy to reach tor hidden services (default: same as -proxy)</source>
<translation>Käytä proxyä tor yhteyksien avaamiseen (vakioasetus: sama kuin -proxy)</translation>
</message>
<message>
<location line="+2"/>
<source>Username for JSON-RPC connections</source>
<translation>Käyttäjätunnus JSON-RPC-yhteyksille</translation>
</message>
<message>
<location line="+4"/>
<source>Warning</source>
<translation>Varoitus</translation>
</message>
<message>
<location line="+1"/>
<source>Warning: This version is obsolete, upgrade required!</source>
<translation>Varoitus: Tämä versio on vanhentunut, päivitys tarpeen!</translation>
</message>
<message>
<location line="+1"/>
<source>You need to rebuild the databases using -reindex to change -txindex</source>
<translation type="unfinished"/>
</message>
<message>
<location line="+1"/>
<source>wallet.dat corrupt, salvage failed</source>
<translation type="unfinished"/>
</message>
<message>
<location line="-50"/>
<source>Password for JSON-RPC connections</source>
<translation>Salasana JSON-RPC-yhteyksille</translation>
</message>
<message>
<location line="-67"/>
<source>Allow JSON-RPC connections from specified IP address</source>
<translation>Salli JSON-RPC yhteydet tietystä ip-osoitteesta</translation>
</message>
<message>
<location line="+76"/>
<source>Send commands to node running on <ip> (default: 127.0.0.1)</source>
<translation>Lähetä käskyjä solmuun osoitteessa <ip> (oletus: 127.0.0.1)</translation>
</message>
<message>
<location line="-120"/>
<source>Execute command when the best block changes (%s in cmd is replaced by block hash)</source>
<translation>Suorita käsky kun paras lohko muuttuu (%s cmd on vaihdettu block hashin kanssa)</translation>
</message>
<message>
<location line="+147"/>
<source>Upgrade wallet to latest format</source>
<translation>Päivitä lompakko uusimpaan formaattiin</translation>
</message>
<message>
<location line="-21"/>
<source>Set key pool size to <n> (default: 100)</source>
<translation>Aseta avainpoolin koko arvoon <n> (oletus: 100)</translation>
</message>
<message>
<location line="-12"/>
<source>Rescan the block chain for missing wallet transactions</source>
<translation>Skannaa uudelleen lohkoketju lompakon puuttuvien rahasiirtojen vuoksi</translation>
</message>
<message>
<location line="+35"/>
<source>Use OpenSSL (https) for JSON-RPC connections</source>
<translation>Käytä OpenSSL:ää (https) JSON-RPC-yhteyksille</translation>
</message>
<message>
<location line="-26"/>
<source>Server certificate file (default: server.cert)</source>
<translation>Palvelimen sertifikaatti-tiedosto (oletus: server.cert)</translation>
</message>
<message>
<location line="+1"/>
<source>Server private key (default: server.pem)</source>
<translation>Palvelimen yksityisavain (oletus: server.pem)</translation>
</message>
<message>
<location line="-151"/>
<source>Acceptable ciphers (default: TLSv1+HIGH:!SSLv2:!aNULL:!eNULL:!AH:!3DES:@STRENGTH)</source>
<translation>Hyväksyttävä salaus (oletus:
TLSv1+HIGH:!SSLv2:!aNULL:!eNULL:!AH:!3DES:@STRENGTH)</translation>
</message>
<message>
<location line="+165"/>
<source>This help message</source>
<translation>Tämä ohjeviesti</translation>
</message>
<message>
<location line="+6"/>
<source>Unable to bind to %s on this computer (bind returned error %d, %s)</source>
<translation>Kytkeytyminen %s tällä tietokonella ei onnistu (kytkeytyminen palautti virheen %d, %s)</translation>
</message>
<message>
<location line="-91"/>
<source>Connect through socks proxy</source>
<translation>Yhdistä socks proxyn läpi</translation>
</message>
<message>
<location line="-10"/>
<source>Allow DNS lookups for -addnode, -seednode and -connect</source>
<translation>Salli DNS kyselyt -addnode, -seednode ja -connect yhteydessä</translation>
</message>
<message>
<location line="+55"/>
<source>Loading addresses...</source>
<translation>Ladataan osoitteita...</translation>
</message>
<message>
<location line="-35"/>
<source>Error loading wallet.dat: Wallet corrupted</source>
<translation>Virhe ladattaessa wallet.dat-tiedostoa: Lompakko vioittunut</translation>
</message>
<message>
<location line="+1"/>
<source>Error loading wallet.dat: Wallet requires newer version of Academiccoin</source>
<translation>Virhe ladattaessa wallet.dat-tiedostoa: Tarvitset uudemman version Academiccoinista</translation>
</message>
<message>
<location line="+93"/>
<source>Wallet needed to be rewritten: restart Academiccoin to complete</source>
<translation>Lompakko tarvitsee uudelleenkirjoittaa: käynnistä Academiccoin uudelleen</translation>
</message>
<message>
<location line="-95"/>
<source>Error loading wallet.dat</source>
<translation>Virhe ladattaessa wallet.dat-tiedostoa</translation>
</message>
<message>
<location line="+28"/>
<source>Invalid -proxy address: '%s'</source>
<translation>Virheellinen proxy-osoite '%s'</translation>
</message>
<message>
<location line="+56"/>
<source>Unknown network specified in -onlynet: '%s'</source>
<translation>Tuntematon verkko -onlynet parametrina: '%s'</translation>
</message>
<message>
<location line="-1"/>
<source>Unknown -socks proxy version requested: %i</source>
<translation>Tuntematon -socks proxy versio pyydetty: %i</translation>
</message>
<message>
<location line="-96"/>
<source>Cannot resolve -bind address: '%s'</source>
<translation>-bind osoitteen '%s' selvittäminen epäonnistui</translation>
</message>
<message>
<location line="+1"/>
<source>Cannot resolve -externalip address: '%s'</source>
<translation>-externalip osoitteen '%s' selvittäminen epäonnistui</translation>
</message>
<message>
<location line="+44"/>
<source>Invalid amount for -paytxfee=<amount>: '%s'</source>
<translation>-paytxfee=<amount>: '%s' on virheellinen</translation>
</message>
<message>
<location line="+1"/>
<source>Invalid amount</source>
<translation>Virheellinen määrä</translation>
</message>
<message>
<location line="-6"/>
<source>Insufficient funds</source>
<translation>Lompakon saldo ei riitä</translation>
</message>
<message>
<location line="+10"/>
<source>Loading block index...</source>
<translation>Ladataan lohkoindeksiä...</translation>
</message>
<message>
<location line="-57"/>
<source>Add a node to connect to and attempt to keep the connection open</source>
<translation>Linää solmu mihin liittyä pitääksesi yhteyden auki</translation>
</message>
<message>
<location line="-25"/>
<source>Unable to bind to %s on this computer. Academiccoin is probably already running.</source>
<translation>Kytkeytyminen %s ei onnistu tällä tietokoneella. Academiccoin on todennäköisesti jo ajamassa.</translation>
</message>
<message>
<location line="+64"/>
<source>Fee per KB to add to transactions you send</source>
<translation>Rahansiirtopalkkio per KB lisätään lähettämääsi rahansiirtoon</translation>
</message>
<message>
<location line="+19"/>
<source>Loading wallet...</source>
<translation>Ladataan lompakkoa...</translation>
</message>
<message>
<location line="-52"/>
<source>Cannot downgrade wallet</source>
<translation>Et voi päivittää lompakkoasi vanhempaan versioon</translation>
</message>
<message>
<location line="+3"/>
<source>Cannot write default address</source>
<translation>Oletusosoitetta ei voi kirjoittaa</translation>
</message>
<message>
<location line="+64"/>
<source>Rescanning...</source>
<translation>Skannataan uudelleen...</translation>
</message>
<message>
<location line="-57"/>
<source>Done loading</source>
<translation>Lataus on valmis</translation>
</message>
<message>
<location line="+82"/>
<source>To use the %s option</source>
<translation>Käytä %s optiota</translation>
</message>
<message>
<location line="-74"/>
<source>Error</source>
<translation>Virhe</translation>
</message>
<message>
<location line="-31"/>
<source>You must set rpcpassword=<password> in the configuration file:
%s
If the file does not exist, create it with owner-readable-only file permissions.</source>
<translation>Sinun täytyy asettaa rpcpassword=<password> asetustiedostoon:
%s
Jos tiedostoa ei ole, niin luo se ainoastaan omistajan kirjoitusoikeuksin.</translation>
</message>
</context>
</TS> | code |
मध्य प्रदेश डिस्ट्रिक्ट न्यूज़ पोर्टल : श्योपुर : २५-अप्रैल-२०१९ : जिला पंचायत के सभागार में व्यय लेखा टीम का प्रशिक्षण आयोजित : कलेक्टर एवं जिला निर्वाचन अधिकारी श्री बसंत कुर्रे के निर्देशन में जिला पंचायत के सीईओ की अध्यक्षता
|| आपदा प्रबंधन संबंधी तैयारी बैठक २५ मई को || नेशनल लोक अदालत संबंधी बैठक आज || पुलिस इन्टर्नशिप योजना हेतु आवेदन आमंत्रित || मतगणना शांतिपूर्ण ढ़ग से जारी || कक्षा १०वीं में पढ़ाने वाले शिक्षकों की परीक्षा १२ जून को || मदरसों की मान्यता का ऑनलाइन होगा नवीनीकरण || अशासकीय स्कूलों में निःशुल्क प्रवेश हेतु ऑनलाईन || लोकसेवा केन्द्रों के टेंडर की प्रक्रिया || समर्थन मूल्य पर गेहूं उपार्जन की अंतिम तिथि २५ मई निर्धारित || केन्द्रीय विद्यालय टीकमगढ़ में ११वीं कक्षा में विज्ञान स्ट्रीम में प्रवेश प्रारंभ
जिला पंचायत के सभागार में व्यय लेखा टीम का प्रशिक्षण आयोजित
श्योपुर | २५-अप्रैल-२०१९
कलेक्टर एवं जिला निर्वाचन अधिकारी श्री बसंत कुर्रे के निर्देशन में जिला पंचायत के सीईओ की अध्यक्षता में लोकसभा निर्वाचन-२०१९ के अंतर्गत गठित की गई जिला स्तरीय व्यय लेखा टीम का प्रशिक्षण आज जिला पंचायत श्योपुर के सभागार में विधानसभा क्षेत्र श्योपुर एवं विजयपुर के अंतर्गत आयोजित किया गया।
इस प्रशिक्षण में डिप्टी कलेक्टर श्री बीबी अग्निहोत्री, स्वीप के सहायक नोडल आॅफिसर डॉ. ओपी शर्मा, मास्टर ट्रेनर श्री नंद बिहारी शर्मा, एवं व्यय लेखा टीम श्योपुर एवं विजयपुर के अधिकारी/कर्मचारी उपस्थित थे।
जिला पंचायत के सीईओ श्री राजेश शुक्ल ने व्यय लेखा टीम के प्रशिक्षण को संबोधित करते हुए कहा कि श्योपुर एवं विजयपुर विधानसभा क्षेत्र के लिए व्यय लेखा की पृथक-पृथक टीमे बनाई गई है। इन टीमों में शामिल अधिकारी/कर्मचारी अभ्यार्थी और पार्टी के लेखा का संधारण व्यवस्थित तरीके से करें। साथ ही विभिन्न टीमों द्वारा दी गई जानकारी के अनुसार संबंधित पार्टी और अभ्यार्थी के खाते में राशि जोड़ने की कार्यवाही सुनिश्चित की जावे।
डिप्टी कलेक्टर श्री बीबी अग्निहोत्री ने प्रशिक्षण में कहा कि लोकसभा निर्वाचन के अंतर्गत व्यय लेखा टीमें अपने दायित्वों का निर्वहन समय-सीमा में सुनिश्चित करें। साथ ही अभ्यार्थी एवं पार्टी के लेखा-जोखा का संधारण करते हुए स्वतंत्र व निष्पक्ष चुनाव संपन्न कराने में सहभागी बने।
प्रशिक्षण में स्वीप के सहायक नोडल ऑफिसर/मास्टर ट्रेनर डॉ. ओपी शर्मा ने व्यय लेखा टीम के प्रशिक्षण में आयोग के निर्देशानुसार कार्यवाही करने पर प्रशिक्षण दिया। साथ ही व्यय लेखा टीमों को राशि जोड़ने की कार्यवाही से अवगत कराया। इसी प्रकार निर्धारित प्रपत्र में जानकारी संक्लित करने की दिशा में अवगत कराया। साथ ही केंद्रीय व्यय प्रेक्षक को रिपोर्ट प्रेषित करने की दिशा में जानकारी दी।
इसी प्रकार मास्टर ट्रेनर श्री नंदबिहारी शर्मा ने व्यय लेखा टीमों के प्रशिक्षण में कहा कि सहायक व्यय प्रेक्षक श्योपुर, विजयपुर विधानसभा के क्षेत्र में पार्टी एवं अभ्यार्थी के खाते में खर्चा को जोड़ने के बारे में अपने कर्तव्यों का निर्वहन करें। | hindi |
अधिकारी ने बताया कि बैतूल जिले (बेतूल डिस्ट्रिक्ट) में कोरोना वायरस से संक्रमित पाया गया व्यक्ति नागपुर में एक जमात में शामिल हुआ था और ३१ मार्च को वहां से वापस लौटा था.
भोपाल. मध्य प्रदेश में कोरोना वायरस (कोरोनाविरस) संक्रमण के ४१ नए मामले सामने आए हैं. इसके साथ ही प्रदेश में इस महामारी से पीड़ित मरीजों की संख्या बढ़कर २५६ पहुंच गयी है. वहीं, दूसरी ओर इन्दौर में ११ लोगों सहित प्रदेश में कुल १८ लोगों को इस संक्रमण से स्वस्थ होने के बाद अस्पताल से छुट्टी दी जा चुकी है. प्रदेश की राजधानी भोपाल (भोपाल) में पिछले २४ घंटे में सबसे अधिक २१ कोरोना संक्रमण के मरीज पाए गए हैं. अब तक भोपाल में कुल ६१ मरीज कोविड-१९ (कोविड-१९) वायरस से संक्रमित पाए गए हैं. प्रदेश में पाए गए २५६ कोरोना मरीजों में से प्रदेश की आर्थिक राजधानी माने जाने वाले शहर इन्दौर से १५१ कोरोना संक्रमित मरीज मिले हैं. जबकि पिछले २४ घंटों में इन्दौर में कोरोना वायरस के १६ नए मरीजों का पता चला है.
व्यक्ति नागपुर में एक जमात में शामिल हुआ था
अधिकारी ने बताया कि बैतूल जिले में कोरोना वायरस से संक्रमित पाया गया व्यक्ति नागपुर में एक जमात में शामिल हुआ था और ३१ मार्च को वहां से वापस लौटा था. इसी प्रकार विदिशा जिले का व्यक्ति असम में जमात के कार्यक्रम में शामिल होकर पिछले माह वापस लौटा था. इस बीच, संबंधित जिले के अधिकारियों ने भैंसदेही और सिंरोज को केंटेनमेंट एरिया घोषित कर दिया है. स्वास्थ्य विभाग के सोमवार शाम को यहां जारी किए गए कोरोना बुलेटिन के अनुसार, प्रदेश में सबसे अधिक १५१ मरीज इन्दौर में, ६१ मरीज भोपाल में, १२ मुरैना में, आठ जबलपुर में, आठ उज्जैन में, चार खरगोन में, तीन बड़वानी में , तथा दो- दो मरीज छिंदवाड़ा, शिवपुरी और ग्वालियर में मिले हैं.
११ लोगों को इन्दौर में अस्पताल से छुट्टी दे दी गयी है
बुलेटिन के अनुसार सोमवार, देर शाम तक प्रदेश में कोरोना वायरस से संक्रमित मरीजों की संख्या बढ़कर २५६ हो गयी है. इस बीच, इस घातक वायरस से ठीक होकर ११ लोगों को इन्दौर में अस्पताल से छुट्टी दे दी गयी है. वहीं प्रदेश में १८ लोगों ने इस वायरस को मात देकर अस्पतालों से विदा ली है. बुलेटिन के अनुसार, प्रदेश में उपचाररत २०८ मरीजों की हालत स्थिर है जबकि २३ मरीजों की हालत गंभीर है. पिछले एक सप्ताह में प्रदेश के स्वास्थ्य विभाग की प्रमुख सचिव सहित दो आईएएस अधिकारी कोरोना वायरस के संक्रमण की चपेट में आ चुके हैं. इसके अलावा कोरोना वायरस की महामारी से निपटने में भोपाल में अपनी ड्यूटी पर लगे स्वास्थ्य और पुलिस विभाग के कुछ अन्य कर्मचारी और अधिकारी भी कोरोना वायरस से संक्रमित पाए गए हैं. | hindi |
इप्ल में राहुल द्रविड़ की खोज, बनेंगे देश की शान! - इप्ल २०१७ आजतक
इप्ल में राहुल द्रविड़ की खोज, बनेंगे देश की शान!
दिल्ली डेयरडेविल्स और गुजरात लॉयंस के बीच खेले गये मैच में अमित मिश्रा के आखिरी ओवर में लगाये गये दो चौकों के कारण दिल्ली को शानदार जीत मिली. जीत के बाद दिल्ली के कोच राहुल द्रविड़ काफी खुश दिखे, और अपनी खुशी का इजहार किया.
भारत के लिए टी-२० खेल चुके १९ साल के ऋषभ पंत ने इस साल आईपीएल में सभी का दिल जीता. हाल ही में गुजरात के खिलाफ उन्होंने ताबड़तोड़ ४३ गेंदों में ९७ रनों की पारी खेली थी, जिसमें उन्होंने ९ छक्के लगाये थे.
पंत लगातार अच्छा प्रदर्शन कर रहे हैं. आईपीएल शुरू होने से पहले पंत के पिता की मौत हो गई थी, जिसके बाद पहले ही मैच में उन्होंने शानदार अर्धशतक जड़ा था.
२२ साल के श्रेयर अय्यर गुजरात के खिलाफ खेले गये मैच के हीरो रहे. उन्होंने ५७ गेंदों में शानदार ९७ रन बनाए, और दिल्ली को जीत की दहलीज़ पर पहुंचाया.
आपको बता दें कि अय्यर शुरुआती आईपीएल मैचों में नहीं खेल पाये थे. उन्हें चेचक की बीमारी थी. अय्यर २०१५ के आईपीएल में इमर्जिंग प्लेयर का खिताब भी जीत चुके हैं. इस साल रणजी ट्रॉफी के दौरान भी श्रेयस ने शानदार प्रदर्शन किया और १३२१ रन बनाये.
पिछले काफी समय से संजू सैमसन पर सभी की निगाहें हैं. दिल्ली की टीम में आने से पहले वह राजस्थान रॉयल्स के साथ थे, और वहां भी अच्छा प्रदर्शन किया था. इस बार भी उन्होंने लगातार अच्छा प्रदर्शन किया है. सैमसन ने पुणे के खिलाफ शानदार ६३ गेंदों में १०३ रन बनाये थे.
शतक के बाद सैमसन ने राहुल द्रविड़ की तारीफ में कहा था कि वह खुशनसीब हैं कि उन्हें राहुल सर से सीखने का मौका मिलता है. आपको बता दें कि दिल्ली डेयरडेविल्स से पहले राहुल द्रविड़ राजस्थान टीम के साथ ही जुड़े थे. | hindi |
KRACH/A Portfolio of Five Works, 1973, edition of 99 plus proofs. Each signed "Alechinsky" in pencil l.r. and numbered "1/99" in pencil l.l., also signed and numbered in red pencil on the inside back cover of the portfolio. Color aquatints with collage on Japan paper, sheet sizes 30 1/4 x 22 1/8 in. (76.8 x 56.0 cm), unmatted, presented in the original portfolio cover.
Condition: Deckled edges, minor creasing/wear to deckles.
Africain subtle toning, slight rippling alone edges of plate mark; Cafe Standard subtle pinpoint foxing u.r., l.r. and l.l. quadrant, Kiew crease u.c. of plate mark to edge of sheet, minor rippling; Portugalpinpoint foxing along lower, upper, and right edges of sheet, subtle accretion u.l. of plate mark, slight rippling along plate mark edges L'Eyrieux pinpoint foxing l.r., subtle rippling. | english |
२९ मई से १ जून के दौरान अरब सागर के ऊपर दबाव पर आईएमडी की रिपोर्ट - रेल्वे एंक्वीरी
जून ३० (२२:००) २९ मई से १ जून के दौरान अरब सागर के ऊपर दबाव पर आईएमडी की रिपोर्ट (पीब.गोव.इन)
भारतीय मौसम विज्ञान विभाग (आईएमडी) के राष्ट्रीय मौसम पूर्वानुमान केंद्र/ क्षेत्रीय मौसम विज्ञान संबंधी केंद्र, नई दिल्ली ने २९...
मई से १ जून के दौरान अरब सागर के ऊपर दबाव पर एक रिपोर्ट जारी की है। रिपोर्ट की कुछ प्रमुख विशेषताओं पर नीचे चर्चा की गई है:
(रिलीज़ आईडी: १६३२८७७) आगंतुक पटल : ११४ | hindi |
// @flow
import R from "ramda"
import casual from "casual-browserify"
import type { Match, Location } from "react-router"
export const arrayN = (min: number, max: number) =>
R.range(0, casual.integer(min, max))
export const randomSelection = (n: number, xs: Array<any>) =>
R.times(() => draw(xs), n)
export const draw = (xs: Array<any>) => xs[casual.integer(0, xs.length - 1)]
export const makeMatch = (url: string): Match => ({
url: url,
isExact: true,
params: {},
path: ""
})
export const makeLocation = (pathname: string): Location => ({
pathname: pathname,
search: "",
hash: ""
})
| code |
settle nuh / version orig.
she's mine / version orig.
pass the chalice / version orig.
fire gun / version orig.
if i did you wrong / i never knew orig.
'water come a me eyes' orig.
'don't throw it all away' orig.
to all the girls / version orig.
you can't be happy orig.
head to toe / version orig.
i remember / version orig.
band new slang / version orig.
'think me did done' orig.
jump up / version orig.
four the hard way orig.
these songs will last forever orig.
talk of the town / talk of dub orig.
it's all the the game / version orig.
make it up to you orig.
i wanna wake up with you orig.
lets keep it that way orig.
try again / more roses orig.
trouble again / float on orig.
how could i live / sax mixs orig.
i'd die without you orig.
land of rydim / version orig. | english |
ماجہ ہنٛدۍ آلو بٔنتھ چھم پتے لاراں سڑک | kashmiri |
یُس شہزادِ مےٚ اَز صُبحس یہِ ؤنِتھ سوٗز زِ یہِ اوس تٔمۍ سٕنٛدِس گُذریمتِس پِترٕ سٕنٛدِ نٲوۍ | kashmiri |
{{\theta}t b}egin{document}
{\theta}itle{On the Calabi-Yau problem for maximal surfaces in $\mathbb{L}^3$}
{\alpha}uthor{Antonio Alarcón}
{\theta}hanks{This research is partially supported by MEC-FEDER Grant no. MTM2004 - 00160.}
\date{{\theta}oday}
{\alpha}ddress{Departamento de Geometría y Topología
{{\theta}t b}reak\indent Universidad de Granada,
{{\theta}t b}reak\indent
18071, Granada
{{\theta}t b}reak\indent Spain}
\email{alarcon@ugr.es}
{{\theta}t b}egin{abstract}
In this paper we construct an example of a maximal surface in the
Lorentz-Minkowski space $\mathbb{L}^3,$ which is bounded by a hyperboloid
and weakly complete in the sense explained by Umehara and Yamada
\cite{Um-Ya}.
\\
\noindent {\em 2000 Mathematics Subject Classification:} Primary 53C50; Secondary 53C42, 53A10, 53B30.
\noindent {\em Keywords:} Complete maximal immersions, maximal
surfaces with singularities.
\end{abstract}
\title{On the Calabi-Yau problem for maximal surfaces in $\L^3$}
{\sigma}ection{Introduction}
A maximal hypersurface in a Lorentzian manifold is a spacelike
hypersurface with zero mean curvature. Besides of their
mathematical interest these hypersurfaces and more generally those
having constant mean curvature have a significant importance in
physics \cite{Kiehn,Kiehn2,MT}. When the ambient space is the
Minkowski space $\mathbb{L}^n,$ one of the most important results is the
proof of a Bernstein-type theorem for maximal hypersurfaces in
$\mathbb{L}^n$. Calabi \cite{Calabi} proved that the only complete
hypersurfaces with zero mean curvature in $\mathbb{L}^3$ (i.e. maximal
surfaces) and $\mathbb{L}^4$ are spacelike hyperplanes, solving the so
called Bernstein-type problem in dimensions 3 and 4. Cheng and Yau
\cite{Ch-Yau} extended this result to $\mathbb{L}^n,$ $n {\gamma}eq 5.$ It is
therefore meaningless to consider global problems on maximal and
everywhere regular hypersurfaces in $\mathbb{L}^n.$ In contrast, there
exists a lot of results about existence of non-flat maximal
surfaces with singularities \cite{Isa-PL1,Isa-PL-RS,LLS}.
\\
It is well known the close relationship between maximal surfaces
in $\mathbb{L}^3$ and minimal surfaces in $\mathbb{R}^3$ (see Remark \ref{minmax}
in page \pageref{minmax}). This fact let us solve some problems on
maximal surfaces by solving the analogous ones for minimal
surfaces, and vice versa. This is not the case of the Calabi-Yau
problem. In 1965 Calabi asked whether or not it is possible for a
complete minimal surface in $\mathbb{R}^3$ to be bounded. Much work has
been done on it over the past four decades. The most important
result in this line was obtained by Nadirashvili \cite{nadi}, who
constructed a complete minimal surface in the unit ball of $\mathbb{R}^3.$
See \cite{salvador} for more information about this topic. From a
Nadirashvili's surface and using the relationship between maximal
and minimal surfaces, we can obtain as most the existence of a
weakly complete maximal surface contained in a cylinder of $\mathbb{L}^3.$
Here, we use the concept of weakly completeness (see definition
\ref{def: weakly} in page \pageref{def: weakly}) that was
introduced by Umehara and Yamada \cite{Um-Ya}.
\\
In this paper, we construct an example of a weakly complete
maximal surface in $\mathbb{L}^3$ with singularities, which is bounded by
a hyperboloid. We would like to point out that our example does
not have branch points, all the singularities are of lightlike
type (see definition \ref{def: light} in page \pageref{def:
light}).
More precisely, we prove the following existence theorem.
{{\theta}t b}egin{theorem}{\lambda}abel{teorema}
There exists a weakly complete conformal maximal immersion with
lightlike singularities of the unit disk into the set
$\{(x,y,z)\in\mathbb{L}^3\;|\;x^2+y^2-z^2<-1\}.$
\end{theorem}
For several reasons, lightlike singularities of maximal surfaces
in $\mathbb{L}^3$ are specially interesting. This kind of singularities
are more attractive than branch points, in the sense that they
have a physical interpretation \cite{Kiehn,Kiehn2}. At these
points, the limit tangent plane is lightlike, the curvature blows
up and the Gauss map has no well defined limit. However, as in the
case of minimal surfaces, if we allow branch points, then proving
the analogous result of Theorem \ref{teorema} has less technical
difficulties.
The fundamental tools used in the proof of this result (Runge's
theorem and the López-Ros transformation) are those that
Nadirashvili utilized to construct the first example of a complete
bounded minimal surface in $\mathbb{R}^3.$ Improvements of his technique
have generated a lot of literature on the Calabi-Yau problem for
minimal surfaces in $\mathbb{R}^3$ \cite{MM-Convex2, MN, AFM}.
\\
Similarly to the case of minimal surfaces, it would be stimulating
to look for an additional property for a weakly complete bounded
maximal surface: properness. In order to achieve it, the technique
showed in this paper could be combined with the reasonings used in
the construction \cite{dga} of a proper conformal maximal disk in
$\mathbb{L}^3,$ following the ideas of \cite{MM-Convex}. The main
objection of this argument is that the best result known about the
convex hull property for maximal surfaces \cite{leo-rosa} needs
the control of the image of the singularities of the surface. This
problem will be studied in \cite{yo-isa}.
{\sigma}ection{Background and notation}
{\sigma}ubsection{The Lorentz-Minkowski three space}
We denote by $\mathbb{L}^3$ the three dimensional Lorentz-Minkowski space
$(\mathbb{R}^3,\escpro{\cdot,\cdot}),$ where
$\escpro{\cdot,\cdot}=dx_1^2+dx_2^2-dx_3^2.$ The Lorentzian {\em
norm} is given by $\|(x_1,x_2,x_3)\|^2=x_1^2+x_2^2-x_3^2,$ and
$\|x\|=\rm{sign}(\|x\|^2){\sigma}qrt{|\|x\|^2|}.$ We say that a vector
$v\in\mathbb{R}^3{\sigma}etminus \{(0,0,0)\}$ is spacelike, timelike or
lightlike if $\|v\|^2$ is positive, negative or zero,
respectively. The vector $(0,0,0)$ is spacelike by definition. A
plane in $\mathbb{L}^3$ is spacelike, timelike or lightlike if the induced
metric is Riemannian, non degenerate and indefinite or degenerate,
respectively.
In order to differentiate between $\mathbb{L}^3$ and $\mathbb{R}^3$, we denote
$\mathbb{R}^3=(\mathbb{R}^3,\escproR{\cdot,\cdot}),$ where $\escproR{\cdot,\cdot}$
is the usual metric of $\mathbb{R}^3$, i.e., $\escproR{\cdot,\cdot}=dx_1^2+dx_2^2+dx_3^2.$
We also denote the Euclidean norm by $\normaR{\cdot}.$
\\
By an (ordered) $\mathbb{L}^3$-orthonormal basis we mean a basis of $\mathbb{R}^3,$ $\{u,v,w\},$ satisfying
{{\theta}t b}egin{itemize}
\item $\escpro{u,v}=\escpro{u,w}=\escpro{v,w}=0$;
\item $\norma{u}=\norma{v}=-\norma{w}=1$.
\end{itemize}
Notice that $u$ and $v$ are spacelike vectors whereas $w$ is
timelike.
\\
We call $\mathbb{H}^2:=\{(x_1,x_2,x_3)\in\mathbb{R}^3 \;|\;
x_1^2+x_2^2-x_3^2=-1\}$ the hyperbolic sphere in $\mathbb{L}^3$ of
constant intrinsic curvature $-1.$ Notice that $\mathbb{H}^2$ has two
connected components $\mathbb{H}^2_+:=\mathbb{H}^2\cap\{x_3{\gamma}eq 1\}$ and
$\mathbb{H}^2_-:=\mathbb{H}^2\cap \{x_3{\lambda}eq -1\}.$ The stereographic projection
$\eta$ for $\mathbb{H}^2$ from the point $(0,0,1)\in\mathbb{H}^2_+$ is the map
$\eta:\mathbb{H}^2{\theta}o \mathbb{C}\cup\{\infty\}{\sigma}etminus \{|z|=1\}$ given by
\[
\eta (x_1,x_2,x_3)=\frac{x_1+{\rm i} x_2}{1-x_3} \;,\quad
\eta(0,0,1)=\infty\;.
\]
Notice that $\eta(\mathbb{H}^2_+)=\{|z|>1\}$ and $\eta(\mathbb{H}^2_-)=\{|z|<1\}.$
Given $r{\gamma}eq 0,$ we denote by ${{\theta}t B}(r)$ as the lower convex domain
determined by the set $\{\|x\|=-r\},$ i.e.,
\[
{{\theta}t B}(r)=\{(x_1,x_2,x_3)\in\mathbb{R}^3 \;|\; \norma{(x_1,x_2,x_3)}<-r\;,\;
x_3<-r \}\;.
\]
We also denote ${{\theta}t b}(r)=\partial {{\theta}t B}(r).$ Observe that
${{\theta}t b}(1)=\mathbb{H}^2_-.$ Moreover, if $r_1<r_2,$ then
$\overline{{{\theta}t B}(r_2)}{\sigma}ubset {{\theta}t B}(r_1)$ and ${{\theta}t b}(r_1)\cap
{{\theta}t b}(r_2)=\emptyset.$
\\
Finally, we define the maps $\mathbb{N}N:{{\theta}t B}(0){\theta}o\mathbb{H}_+^2$ and
$\mathbb{N}N_0:{{\theta}t B}(0){\theta}o\mathbb{S}^2$ by the following way. Consider $p\in B(0)$
and label $r=\|p\|<0.$ Let $\mathbb{N}N^r:{{\theta}t b}(r){\theta}o\mathbb{H}^2_+$ and
$\mathbb{N}N_0^r:{{\theta}t b}(r){\theta}o \mathbb{S}^2$ be the outward pointing $\mathbb{L}^3$-normal
Gauss map and the Euclidean outward pointing unit normal of
$b(r),$ respectively. Then, we define
\[
\mathbb{N}N(p)=\mathbb{N}N^r(p)\;,\quad \mathbb{N}N_0(p)=\mathbb{N}N_0^r(p) \;.
\]{\lambda}abel{pag: normales}
Equivalently, $\mathbb{N}N(p)=-p/\norma{p}$ and
$\mathbb{N}N_0(p)=\mathcal{J}(p)/\normaR{p},$ where
$\mathcal{J}(p_1,p_2,p_3)=(p_1,p_2,-p_3).$ Hence, both maps are
differentiable and
$\mathbb{N}N_0(p)=-\mathcal{J}(\mathbb{N}N(p))/\normaR{\mathbb{N}N(p)}.$
{\sigma}ubsection{Maximal surfaces}
Any conformal maximal immersion $X:M{\theta}o\mathbb{L}^3$ is given by a triple
$\Phi=(\Phi_1,\Phi_2,\Phi_3)$ of holomorphic 1-forms defined on
the Riemann surface $M,$ having no common zeros and satisfying
{{\theta}t b}egin{equation}{\lambda}abel{2}
|\Phi_1|^2+|\Phi_2|^2-|\Phi_3|^2\neq 0\;;
\end{equation}
{{\theta}t b}egin{equation}{\lambda}abel{conforme}
\Phi_1^2+\Phi_2^2-\Phi_3^2=0\;;
\end{equation}
and all periods of the $\Phi_j$ are purely imaginary. Here we
consider $\Phi_i$ to be a holomorphic function times $dz$ in a
local parameter $z.$ Then, the maximal immersion $X:M{\theta}o\mathbb{L}^3$ can
be parameterized by $z\mapsto \mbox{\rm Re} \int^z \Phi.$ The above triple
is called the Weierstrass representation of the maximal immersion
$X.$ Usually, the second requirement \eqref{conforme} is
guaranteed by the introduction of the formulas
\[
\Phi_1=\frac{{\rm i}}{2}(1-g^2)\eta\;,\quad \Phi_2=-\frac12(1+g^2)\eta\;,\quad \Phi_3=g\eta
\]
for a meromorphic function $g$ with $|g(p)|\neq 1,$ $\forall p\in
M,$ (the stereographically projected Gauss map) and a holomorphic
1-form $\eta.$ We also call $(g,\eta)$ or $(g,\Phi_3)$ the
Weierstrass representation of $X.$
{{\theta}t b}egin{remark}{\lambda}abel{minmax}
If $(\Phi_1,\Phi_2,\Phi_3)$ is the Weierstrass representation of a
maximal surface, then $({\rm i} \Phi_1,{\rm i} \Phi_2, \Phi_3)$ are the
Weierstrass data of a minimal surface in $\mathbb{R}^3$ \cite{osserman}.
Moreover, both surfaces have the same meromorphic Gauss map $g.$
\end{remark}
We are going to deal with maximal immersions with lightlike
singularities, according with the following definition.
{{\theta}t b}egin{definition}{\lambda}abel{def: light}
A point $p\in M$ is a lightlike singularity of the immersion $X$
if it is not a branch point and $|g(p)|=1.$
\end{definition}
In this article, all the maximal immersions are defined on simply
connected domains of $\mathbb{C},$ thus the Weierstrass 1-forms have no
periods and so the only requirements are \eqref{2} at the points
that are not singularities, and \eqref{conforme}. In this case,
the differential $\eta$ can be written as $\eta =f(z)dz.$ The
metric of $X$ can be expressed as
{{\theta}t b}egin{equation}{\lambda}abel{metrica}
ds^2=\frac12 (|\Phi_1|^2+|\Phi_2|^2-|\Phi_3|^2)={{\theta}t b}ig( \frac12 (1-|g|^2)|f||dz| {{\theta}t b}ig)^2\;.
\end{equation}
We use a concept of completeness that is less exigent than the
classical one. The following definition was given by Umehara and
Yamada \cite{Um-Ya}.
{{\theta}t b}egin{definition}{\lambda}abel{def: weakly}
A maximal immersion $X:M{\theta}o\mathbb{L}^3$ is weakly complete if the Riemann
surface $M$ is complete with the metric
{{\theta}t b}egin{equation}{\lambda}abel{metricaUY}
d{\sigma}igma^2=\frac12 (|\Phi_1|^2+|\Phi_2|^2+|\Phi_3|^2)={{\theta}t b}ig( \frac12
(1+|g|^2)|f||dz| {{\theta}t b}ig)^2\;.
\end{equation}
The metric $d{\sigma}igma^2$ will be called the lift metric of $X.$
\end{definition}
The Euclidean metric on $\mathbb{C}$ is denoted as $\escpro{,}=|dz|^2.$
Note that $ds^2=({\lambda}_X)^2\,|dz|^2$ and
$d{\sigma}igma^2=({\lambda}^0_X)^2\,|dz|^2$ where the conformal coefficients
${\lambda}_X$ and ${\lambda}^0_X$ are given by \eqref{metrica} and
\eqref{metricaUY}, respectively.
{{\theta}t b}egin{remark}{\lambda}abel{rem: branch}
Observe that if $X$ has a singularity of lightlike type in a point
$z\in M,$ then ${\lambda}_X(z)=0$ but ${\lambda}_X^0(z)\neq 0.$ On the other
hand, if $z$ is a branch point of $X,$ one has
${\lambda}_X(z)=0={\lambda}_X^0(z).$
\end{remark}
Along this paper, we use some $\mathbb{L}^3$-orthonormal bases. Given
$X:{\Omega}ega{\theta}o\mathbb{L}^3$ a maximal immersion and $S$ an
$\mathbb{L}^3$-orthonormal basis, we write the Weierstrass data of $X$ in
the basis $S$ as
\[
\Phi_{(X,S)}=(\Phi_{(1,S)},\Phi_{(2,S)},\Phi_{(3,S)})\;, \quad
f_{(X,S)}\;, \quad g_{(X,S)}\;, \quad \eta_{(X,S)}\;.
\]
In the same way, given $v\in\mathbb{R}^3,$ we denote by $v_{(k,S)}$ the
$k$th coordinate of $v$ in $S.$ We also represent by
$v_{(*,S)}=(v_{(1,S)},v_{(2,S)})$ the first two coordinates of $v$
in the basis $S.$
\\
Given a curve ${\alpha}$ in ${\Omega},$ by $\operatorname{length} ({\alpha},ds)$ we mean the
length of ${\alpha}$ with respect to the metric $ds.$ Let $W{\sigma}ubset {\Omega}$
be a subset, then we define
{{\theta}t b}egin{itemize}
\item $\operatorname{dist}_{(W,ds)}(p,q)=\inf \{\operatorname{length} ({\alpha},ds) \;|\; {\alpha}:[0,1]{\theta}o W,$ ${\alpha}(0)=p,$ ${\alpha}(1)=q\},$ for any $p,q\in W.$
\item $\operatorname{dist}_{(W,ds)}(U,V)= \inf \{ \operatorname{dist}_{(W,ds)}(p,q) \;|\; p\in U,$ $q\in V\},$ for any $U,V{\sigma}ubset W.$
\end{itemize}
Given a domain $D{\sigma}ubset \mathbb{C},$ we say that a function, or a 1-form,
is harmonic, holomorphic, meromophic, ... on $\overline{D}$, if it
is harmonic, holomorphic, meromorphic, ... on a domain containing
$\overline{D}.$
Let $P$ be a simple closed polygonal curve in $\mathbb{C}$. By $\operatorname{Int} P$
we mean the bounded connected component of $\mathbb{C}{\sigma}etminus P.$ For a
small enough $\xi>0,$ we denote by $P^\xi$ as the parallel
polygonal curve in $\operatorname{Int} P,$ satisfying that the distance between
parallel sides is equal to $\xi.$ Whenever we write $P^\xi$ we are
assuming that $\xi$ is small enough to define the polygon
properly.
{\sigma}ubsection{The López-Ros transformation}
The proof of Lemma \ref{lema} exploits what has come to be call
the López-Ros transformation. If $(g,f)$ are the Weierstrass data
of a maximal immersion $X:{\Omega}ega{\theta}o\mathbb{L}^3$ (being ${\Omega}ega$ simply
connected), we define on ${\Omega}ega$ the data
\[
\widetilde{g}=\frac{g}{h}\;,\quad \widetilde{f}=f\,h\;,
\]
where $h:{\Omega}ega{\theta}o\mathbb{C}$ is a holomorphic function without zeros.
Observe that the new meromorphic data satisfy \eqref{2} at the
regular points, and \eqref{conforme}, so the new data define a
maximal immersion (possibly with different lightlike
singularities) $\widetilde{X}:{\Omega}ega{\theta}o\mathbb{L}^3.$ This method provides
us with a powerful and natural tool for deforming maximal
surfaces. One of the most interesting properties of the resulting
surface is that the third coordinate function is preserved.
{\sigma}ection{Proof of Theorem \ref{teorema}}
In order to prove Theorem \ref{teorema} we will apply the
following technical Lemma. It will be proved later in Section
\ref{sec: lema}.
{{\theta}t b}egin{lemma}{\lambda}abel{lema}
Consider $r>0,$ $P$ a polygon in $\mathbb{C}$ and $X:\overline{\operatorname{Int} P}{\theta}o
\mathbb{L}^3$ a conformal maximal immersion (possibly with lightlike
singularities) satisfying
{{\theta}t b}egin{equation}{\lambda}abel{ecu: X-cota}
X(\overline{\operatorname{Int} P}){\sigma}ubset {{\theta}t B}(r)\;.
\end{equation}
Let ${\epsilon}$ and
$s$ be positive constants with ${\sigma}qrt{r^2-4s^2}-{\epsilon}>0.$ Then,
there exist a polygon $Q$ and a conformal maximal immersion
(possibly with lightlike singularities) $Y:\overline{\operatorname{Int}
Q}{\theta}o\mathbb{L}^3$ such that
{{\theta}t b}egin{enumerate}[\rm ({L}.1)]
\item $\overline{\operatorname{Int} P^{\epsilon}}{\sigma}ubset \operatorname{Int} Q{\sigma}ubset \overline{\operatorname{Int} Q}{\sigma}ubset \operatorname{Int} P.$
\item $s<\operatorname{dist}_{(\overline{\operatorname{Int} Q},d{\sigma}igma_Y^2)}(P^{\epsilon},Q),$ where
$d{\sigma}igma_Y^2$ is the lift metric associated to the immersion $Y.$
\item $Y(\overline{\operatorname{Int} Q}){\sigma}ubset {{\theta}t B}(R),$ where
$R={\sigma}qrt{r^2-4s^2}-{\epsilon}.$
\item $\|Y-X\|_0<{\epsilon}$ in $\overline{\operatorname{Int} P^{\epsilon}}.$
\end{enumerate}
\end{lemma}
Using this Lemma, we construct a sequence of immersions
$\{\psi_n\}_{n\in\mathbb{N}}$ that converges to an immersion $\psi$ which
proves Theorem \ref{teorema}, up to a reparametrization of its
domain.
First of all, we consider a sequence of reals $\{{\alpha}_n\}_{n\in\mathbb{N}}$
satisfying
\[
\prod_{k=1}^\infty {\alpha}_k=\frac12\;,\quad 0<{\alpha}_k<1\;,\quad \forall
k\in\mathbb{N}\;.
\]
Moreover, we choose $r_1>1$ large enough so that the sequence
$\{r'_n\}_{n\in\mathbb{N}}$ given by
\[
r'_1=r_1\;,\quad r'_n={\sigma}qrt{(r'_{n-1})^2-(2/n)^2}-\frac1{n^2}
\]
satisfies
{{\theta}t b}egin{equation}{\lambda}abel{ecu: r'}
r'_n>1\;,\quad \forall n\in\mathbb{N}\;.
\end{equation}
Now, we are going to construct a sequence
$\{\Upsilon_n\}_{n\in\mathbb{N}},$ where the element
\[
\Upsilon_n=\{P_n,\psi_n,{\epsilon}_n,\xi_n\}
\]
is composed of a polygon $P_n,$ a conformal maximal immersion
$\psi_n:\overline{\operatorname{Int} P_n}{\theta}o\mathbb{L}^3,$ and ${\epsilon}_n<\frac1{n^2},$ and
$\xi_n$ are positive real numbers. We will choose ${\epsilon}_n$ and
$\xi_n$ so that the sequences $\{{\epsilon}_n\}_{n\in\mathbb{N}}$ and
$\{\xi_n\}_{n\in\mathbb{N}}$ decrease to zero.
We construct the sequence in order to satisfy the following list
of properties.
{{\theta}t b}egin{enumerate}[\rm (A{$_n$})]
\item $\overline{\operatorname{Int} P_{n-1}^{\xi_{n-1}}} {\sigma}ubset \operatorname{Int}
P_{n-1}^{{\epsilon}_{n}}{\sigma}ubset \overline{\operatorname{Int} P_{n-1}^{{\epsilon}_{n}}}{\sigma}ubset
\operatorname{Int} P_{n}^{\xi_{n}}{\sigma}ubset \overline{\operatorname{Int} P_{n}^{\xi_{n}}}
{\sigma}ubset \operatorname{Int} P_n{\sigma}ubset \overline{\operatorname{Int} P_n}{\sigma}ubset \operatorname{Int}
P_{n-1}.$
\item $1/n<\operatorname{dist}_{{{\theta}t b}ig(\overline{\operatorname{Int}
P_n^{\xi_n}}\,,\,d{\sigma}igma_{\psi_n}^2{{\theta}t b}ig)}(P_{n-1}^{\xi_{n-1}},P_n^{\xi_n}),$
where $d{\sigma}igma_{X_n}^2$ is the lift metric of the immersion
$\psi_n.$
\item $\psi_n(\overline{\operatorname{Int} P_n}){\sigma}ubset {{\theta}t B}(r_n),$ where
$r_n={\sigma}qrt{r_{n-1}^2-(2/n)^2}-{\epsilon}_n.$ Notice that \eqref{ecu: r'}
guarantees that $\{r_n\}_{n\in\mathbb{N}}$ decreases to a real number
$r_\infty> 1.$
\item $\|\psi_n-\psi_{n-1}\|_0<{\epsilon}_n$ in $\overline{\operatorname{Int}
P_{n-1}^{{\epsilon}_n}}.$
\item ${\lambda}^0_{\psi_n}{\gamma}eq {\alpha}_n\cdot {\lambda}^0_{\psi_{n-1}}$ in $\overline{\operatorname{Int}
P_{n-1}^{\xi_{n-1}}}.$
\end{enumerate}
The sequence $\{\Upsilon_n\}_{n\in\mathbb{N}}$ is constructed in a
recursive way. The existence of a family $\Upsilon_1$ satisfying
assertion (C$_1$) is straightforward. The rest of the properties
have no sense for $n=1.$
Suppose that we have $\Upsilon_1,{\lambda}dots,\Upsilon_n.$ We are going
to construct $\Upsilon_{n+1}.$ We choose a decreasing sequence of
positive reals $\{{\varepsilon}_m\}_{m\in\mathbb{N}}{\sigma}earrow 0$ with
${\varepsilon}_m<\min\{1/(n+1)^2,{\epsilon}_n\}$ for all $m\in\mathbb{N}.$ For each $m,$ we
consider the polygon $Q_m$ and the conformal maximal immersion
$Y_m:\overline{\operatorname{Int} Q_m}{\theta}o\mathbb{L}^3$ given by Lemma \ref{lema} for
the following data:
\[
r=r_n\;,\quad P=P_n\;,\quad X=X_n\;,\quad {\epsilon}={\varepsilon}_m\;,\quad
s=\frac1{n+1}\;.
\]
For a large enough $m,$ (L.1) in Lemma \ref{lema} guarantees that
$\overline{\operatorname{Int} P_n^{\xi_n}}{\sigma}ubset \operatorname{Int} Q_m.$ Moreover, from
Property (L.4), we deduce that the sequence $\{Y_m\}_{m\in\mathbb{N}}$
uniformly converges to $\psi_n$ in $\overline{\operatorname{Int}
P_n^{{\varepsilon}_m}}{\sigma}upset \overline{\operatorname{Int} P_n^{\xi_n}}.$ Then, taking
into account that $Y_m$ is a harmonic map and that its Weierstrass
data are given by its derivatives, we conclude that the sequence
$\{{\lambda}^0_{Y_m}\}_{m\in\mathbb{N}}$ uniformly converges to ${\lambda}^0_{\psi_n}$
in $\overline{\operatorname{Int} P_n^{\xi_n}}.$ Hence, there exists $m_0\in\mathbb{N}$
satisfying
{{\theta}t b}egin{equation}{\lambda}abel{ecu: duke28}
\overline{\operatorname{Int} P_n^{\xi_n}}{\sigma}ubset \operatorname{Int} P_n^{{\varepsilon}_{m_0}}{\sigma}ubset
\overline{\operatorname{Int} P_n^{{\varepsilon}_{m_0}}} {\sigma}ubset \operatorname{Int} Q_{m_0}\;,
\end{equation}
{{\theta}t b}egin{equation}{\lambda}abel{ecu: duke29}
{\lambda}^0_{Y_{m_0}}{\gamma}eq {\alpha}_{n+1}\cdot {\lambda}^0_{\psi_n}\;,\quad {\theta}ext{in
}\overline{\operatorname{Int} P_n^{\xi_n}}\;.
\end{equation}
In order to obtain \eqref{ecu: duke29} we have taken into account
that the immersion $\psi_n$ has no branch points, it only has
singularities of lightlike type (see Remark \ref{rem: branch}).
At this point, we define $P_{n+1}=Q_{m_0},$ $\psi_{n+1}=Y_{m_0}$
and ${\epsilon}_{n+1}={\varepsilon}_{m_0}.$ From (L.2) in Lemma \ref{lema}, we
conclude that $1/(n+1)<\operatorname{dist}_{{{\theta}t b}ig(\overline{\operatorname{Int}
P_{n+1}}\,,\,d{\sigma}igma_{\psi_{n+1}}^2{{\theta}t b}ig)}(P_n^{{\epsilon}_{n+1}},P_{n+1}).$
Therefore, taking into account \eqref{ecu: duke28} we can take
$\xi_{n+1}$ small enough so that (A$_{n+1}$) and (B$_{n+1}$) hold.
Properties (C$_{n+1}$) and (D$_{n+1}$) are consequence of (L.3)
and (L.4), respectively, whereas \eqref{ecu: duke29} implies
(E$_{n+1}$). This concludes the construction of the sequence
$\{\Upsilon_n\}_{n\in\mathbb{N}}.$
\\
Now, define $\mathbb{D}elta:=\cup_{n\in\mathbb{N}}\operatorname{Int} P_n^{{\epsilon}_{n+1}}=
\cup_{n\in \mathbb{N}}\operatorname{Int} P_n^{\xi_n}.$ Since (A$_n$), the set $\mathbb{D}elta$
is an expansive union of simply connected domains resulting in
$\mathbb{D}elta$ being simply connected. Moreover, $\mathbb{D}elta$ is bounded
since Properties (A$_n$), $n\in\mathbb{N}$, so it is biholomorphic to a
disk. On the other hand, from (D$_n$) we obtain that
$\{\psi_n\}_{n\in\mathbb{N}}$ is a Cauchy sequence, uniformly on compact
sets of $\mathbb{D}elta.$ Then, Harnack's Theorem guarantees the existence
of a harmonic map $\psi:\mathbb{D}elta{\theta}o\mathbb{L}^3$ such that
$\{\psi_n\}_{n\in\mathbb{N}}{\theta}o\psi,$ uniformly on compact sets of
$\mathbb{D}elta.$ Then, $\psi$ has the following properties.
\\
${{\theta}t b}ullet$ {\em $\psi$ is maximal and conformal.} This facts are
consequence of that $\psi$ is harmonic.
\\
${{\theta}t b}ullet$ {\em $\psi$ has no branch points.} For any $z\in\mathbb{D}elta$
there exists $n\in\mathbb{N}$ so that $z\in \operatorname{Int} P_n^{\xi_n}.$ Given
$k>n$ and using (E$_j$), $j=n+1,{\lambda}dots,k,$ one has
${\lambda}^0_{\psi_k}(z){\gamma}eq {\alpha}_k\cdots{\alpha}_1 {\lambda}^0_{\psi_n}(z).$ Hence,
taking the limit as $k{\theta}o\infty,$ we infer that
\[
{\lambda}^0_\psi(z){\gamma}eq \frac12 {\lambda}^0_{\psi_n}(z)>0\;,
\]
and so, $\psi$ has no branch points. Notice that the last
inequality holds because of $\psi_n$ has no branch points.
{{\theta}t b}egin{remark}
Observe that this argument does not work if we use the conformal
coefficients ${\lambda}_{\psi_k}$ instead of ${\lambda}^0_{\psi_k}.$ This fact
is implied by the possible existence of singularities of lightlike
type.
\end{remark}
${{\theta}t b}ullet$ {\em $\psi$ is weakly complete.} This fact follows from
Properties (B$_n$), (E$_n$), $n\in\mathbb{N},$ and the fact that the sum
${\sigma}um_{n=1}^\infty 1/n$ diverges.
\\
${{\theta}t b}ullet$ {\em $\psi(\mathbb{D}elta){\sigma}ubset {{\theta}t B}(1).$} Let $z\in\mathbb{D}elta$ and
$n\in\mathbb{N}$ such that $z\in \operatorname{Int} P_n^{\xi_n}.$ For each $k{\gamma}eq n,$
Property (C$_k$) guarantees that $\psi_k(z)\in {{\theta}t B}(r_k){\sigma}ubset
{{\theta}t B}(r_\infty).$ Taking limit as $k{\theta}o\infty,$ we obtain $\psi(z)\in
\overline{{{\theta}t B}(r_\infty)}{\sigma}ubset {{\theta}t B}(1).$
\\
This completes the proof of Theorem \ref{teorema}.
{\sigma}ection{Proof of Lemma \ref{lema}}{\lambda}abel{sec: lema}
The first step of the proof consists of the construction of a
labyrinth on $\operatorname{Int} P$ which depends on the polygon $P$ and a
positive integer $N.$ Let $\ell$ be the number of sides of $P.$
From now on, $N$ is a positive multiple of $\ell.$ Although $N$ is
fix, we will assume along the proof of the lemma that we have
taken it large enough so that some inequalities hold. Without loss
of generality, we assume $0\in \operatorname{Int} P^{\epsilon}.$
{{\theta}t b}egin{remark}
Throughout the proof of the lemma, a set of positive real
constants depending on the data of the lemma, i.e., $r,$ $P,$ $X,$
${\epsilon}$ and $s,$ will appear. The symbol ``${\tt const}$'' will denote
these different constants. It is important to note that the choice
of these constants does not depend on $N.$
\end{remark}
First of all, consider $\zeta_0\in]0,{\epsilon}[.$ Therefore,
$P^{\zeta_0}$ is well defined and $\overline{\operatorname{Int} P^{\epsilon}}{\sigma}ubset
\operatorname{Int} P^{\zeta_0}.$ We also assume that $N$ satisfies
$2/N<\zeta_0.$
Let $v_1,{\lambda}dots,v_{2N}$ be a set of points in the polygon $P$
(containing the vertices of $P$) which divides each side of $P$
into $2N/\ell$ equal parts. Let $v'_1,{\lambda}dots, v'_{2N}$ the points
resulting from transfering the above partition to the polygon
$P^{2/N}.$ Then, we define the following sets.
{{\theta}t b}egin{itemize}
\item $L_i$ is the segment that joins $v_i$ and $v_i',$
$i=1,{\lambda}dots,2N.$
\item $\mathcal{G}_i=P^{i/N^3},$ $i=0,{\lambda}dots,2N^2.$
\item $\mathcal{A}={{\theta}t b}igcup_{i=0}^{N^2-1}\overline{(\operatorname{Int} \mathcal{G}_{2i}){\sigma}etminus (\operatorname{Int}
\mathcal{G}_{2i+1})}$ and
$\widetilde{\mathcal{A}}={{\theta}t b}igcup_{i=1}^{N^2}\overline{(\operatorname{Int}
\mathcal{G}_{2i-1}){\sigma}etminus (\operatorname{Int} \mathcal{G}_{2i})}.$
\item $\mathcal{R}={{\theta}t b}igcup_{i=0}^{2N^2}\mathcal{G}_i.$
\item $\mathcal{B}={{\theta}t b}igcup_{i=1}^N L_{2i}$ and $\widetilde{\mathcal{B}}={{\theta}t b}igcup_{i=0}^{N-1} L_{2i+1}.$
\item $\mathcal{L}=\mathcal{B}\cap \mathcal{A},$ $\widetilde{\mathcal{L}}=\widetilde{\mathcal{B}}\cap
\widetilde{\mathcal{A}}$ and
$H=\mathcal{R}\cup\mathcal{L}\cup\widetilde{\mathcal{L}}.$
\item ${\Omega}_N=\{z\in (\operatorname{Int} \mathcal{G}_0){\sigma}etminus(\operatorname{Int}
\mathcal{G}_{2N^2})\;|\;
\operatorname{dist}_{(\mathbb{C},\escpro{\cdot,\cdot})}(z,H){\gamma}eq 1/(4N^3)\}.$
\item ${\omega}_i$ is the union of the segment $L_i$ and those
connected components of ${\Omega}_N$ that have nonempty intersection
with $L_i,$ for $i=1,{\lambda}dots,2N.$
\item $\varpi_i=\{z\in\mathbb{C}\;|\;
\operatorname{dist}_{(\mathbb{C},\escpro{\cdot,\cdot})}(z,{\omega}_i)<{\delta}(N)\},$ is chosen so
that the sets $\overline{\varpi_i},$ $i=1,{\lambda}dots,2N,$ are pairwise
disjoint.
\end{itemize}
{{\theta}t b}egin{figure}[htbp]
{{\theta}t b}egin{center}
\includegraphics[width=0.70{\theta}extwidth]{laberinto.eps}
\end{center}
\caption{The labyrinth.} {\lambda}abel{fig: 1}
\end{figure}
After constructing the labyrinth, we are going to list some of its
properties.
{{\theta}t b}egin{claim}{\lambda}abel{cla: abcd}
If $N$ is large enough, for any $i=1,{\lambda}dots,2N,$ one has
{{\theta}t b}egin{enumerate}[\rm A.]
\item $\operatorname{diam}_{(\mathbb{C},\escpro{\cdot,\cdot})}(\varpi_i)<{\tt const}/N.$
\item $\operatorname{diam}_{\mathbb{H}_+^2}
(\mathbb{N}N(X(\varpi_i)))<1/{\sigma}qrt{N},$ where $\operatorname{diam}_{\mathbb{H}^2_+}$ is the
intrinsic diameter in $\mathbb{H}^2_+.$ Here, $\mathbb{N}N$ is the map defined in
page \pageref{pag: normales}.
\item Denote by $(g,\Phi_3)$ the Weierstrass data of the immersion $X.$ Then,
there exists a subset $I_0{\sigma}ubset \{1,{\lambda}dots,2N\}$ such that
{{\theta}t b}egin{itemize}
\item $|g(z)|\neq 1$ $\forall z\in \varpi_j,$ $\forall j\in I_0.$
\item $g(z)\neq \infty$ $\forall z\in\varpi_j,$ $\forall j\in
J_0=\{1,{\lambda}dots,2N\}{\sigma}etminus I_0.$
\end{itemize}
\item Let ${\lambda}^2 \escpro{\cdot,\cdot}$ be a conformal metric in
$\overline{\operatorname{Int} P}.$ Assume there exists $c\in\mathbb{R}^+$ so that
\[
{\lambda}{\gamma}eq
{{\theta}t b}egin{cases}
c & {\theta}ext{in }\operatorname{Int} P\;,
\\
c\,N^4 & {\theta}ext{in }{\Omega}_N\;.
\end{cases}
\]
Then, for any curve ${\alpha}$ in $\overline{\operatorname{Int} P}$ connecting
$P^{\zeta_0}$ and $P,$ one has
$\operatorname{length}({\alpha},{\lambda}\escpro{\cdot,\cdot})>{\tt const} \,c\,N,$ where ${\tt const}$
does not depend on $c.$
\end{enumerate}
\end{claim}
{{\theta}t b}egin{proof}
Checking Item A in the above claim is straightforward. Item B is a
consequence of Item A and the fact that $\mathbb{N}N$ is a differentiable
map. For a suffienctly large $N,$ Item C holds since Item A and
because of $g$ is a meromorphic function. In order to prove Item
D, we denote by ${\alpha}_j$ as the piece of ${\alpha}$ connecting $P^{j/N}$
and $P^{(j+1)/N},$ for $j=0,{\lambda}dots,N^2-1.$ Then, either the
Euclidean length of ${\alpha}_j$ is greater than ${\tt const}/N$ or the length
of ${\alpha}_j\cap {\Omega}_N$ is greater than $1/2N^3.$ This fact and our
assumption about ${\lambda}$ imply Item D.
\end{proof}
At this point, we construct a sequence $F_0=X,F_1,{\lambda}dots, F_{2N}$
of conformal maximal immersions (with boundary and, possibly,
lightlike singularities) defined in $\overline{\operatorname{Int} P}.$
{{\theta}t b}egin{claim}{\lambda}abel{cla: 5.2}
We will construct the sequence in order to satisfy the
following list of statements, for $i=1,{\lambda}dots,2N.$
{{\theta}t b}egin{enumerate}[\rm ({a}1$_{i}$)]
\item $F_i(z)=\mbox{\rm Re}{{\theta}t b}ig( \int_0^z \phi^i(u)\,du{{\theta}t b}ig)+V.$
Here, $V\in \mathbb{R}^3$ is a fixed vector. It does not depend on $i.$
\item $\normaR{\phi^i-\phi^{i-1}}{\lambda}eq 1/N^2$ in $\overline{\operatorname{Int}
P}{\sigma}etminus \varpi_i.$
\item $\normaR{\phi^i}{\gamma}eq N^{7/2}$ in ${\omega}_i.$
\item $\normaR{\phi^i}{\gamma}eq {\tt const}/{\sigma}qrt{N}$ in $\varpi_i.$
\item Assume $(g_i,\phi^i_3)$ are the Weierstrass data of
$F_i.$ Then, the following two assertions hold.
{{\theta}t b}egin{enumerate}[\rm ({a5.}1$_{i}$)]
\item $|g_i(z)|\neq 1,$ $\forall z\in\varpi_j,$ $\forall j\in
I_0,$ $j>i.$ Hence, the Gauss map $G_i$ of the immersion $F_i$ is
well defined in $\varpi_j$ for those $j.$ Moreover,
$\operatorname{dist}_{\mathbb{H}^2}(G_i(z),G_{i-1}(z))<1/N^2,$ for any $z\in\varpi_j$
and for any $j\in I_0,$ $j>i,$ where by $\operatorname{dist}_{\mathbb{H}^2}$ we mean the
intrinsic distance in $\mathbb{H}^2.$
\item $g_i(z)\neq \infty,$ $\forall z\in\varpi_j,$ $\forall j\in
J_0,$ $j>i.$ Furthermore, one has $|g_i(z)-g_{i-1}(z)|<1/N^2,$ for
any $z\in\varpi_j,$ for any of those $j.$
\end{enumerate}
\item There exists $S_i=\{e_1,e_2,e_3\}$ an orthonormal frame in
$\mathbb{L}^3,$ such that
{{\theta}t b}egin{enumerate}[\rm ({a6.}1$_{i}$)]
\item $\operatorname{dist}_{\mathbb{H}^2_+}(e_3,\mathbb{N}N(X(z))<{\tt const}/{\sigma}qrt{N},$ for any $z\in
\overline{\varpi_i}.$
\item $(F_i(z))_{(3,S_i)}=(F_{i-1}(z))_{(3,S_i)},$ for all $z$ in
$\overline{\operatorname{Int} P}.$
\end{enumerate}
\item $\normaR{F_i-F_{i-1}}<{\tt const}/N^2$ in $(\operatorname{Int} P){\sigma}etminus
\varpi_i.$
\end{enumerate}
\end{claim}
{{\theta}t b}egin{proof}
The sequence $F_0,F_1,{\lambda}dots,F_{2N}$ is constructed in a recursive
way. Assume that we already have $F_0,F_1,{\lambda}dots,F_{j-1}$
satisfying the assertions (a1$_i$),${\lambda}dots,$ (a7$_i$),
$i=1,{\lambda}dots,j-1.$ Before constructing $F_j,$ we need to check the
following claim.
{{\theta}t b}egin{claim}{\lambda}abel{cla: 5.3}
For a large enough $N,$ the following statements hold.
{{\theta}t b}egin{enumerate}[\rm ({b}1)]
\item $\normaR{\phi^{j-1}}{\lambda}eq {\tt const}$ in $(\operatorname{Int} P){\sigma}etminus
({{\theta}t b}igcup_{k=1}^{j-1} \varpi_k).$
\item $\normaR{\phi^{j-1}}{\gamma}eq {\tt const}$ in $(\operatorname{Int} P){\sigma}etminus
({{\theta}t b}igcup_{k=1}^{j-1} \varpi_k).$
\item The diameter in $\mathbb{R}^3$ of $F_{j-1}(\varpi_j)$ is less than
$1/{\sigma}qrt{N}.$
\item Assume $j\in I_0.$ Then,
{{\theta}t b}egin{enumerate}
\item[\rm ({b4.}1)] The diameter in $\mathbb{H}^2$ of $G_{j-1}(\varpi_j)$
is less than $1/{\sigma}qrt{N}.$ In particular, there exists $p\in
G_{j-1}(\varpi_j)$ such that
$\operatorname{dist}_{\mathbb{H}^2}(p,G_{j-1}(z))<1/{\sigma}qrt{N},$ for any $z\in \varpi_j.$
\end{enumerate}
On the other hand, suppose $j\in J_0.$
{{\theta}t b}egin{enumerate}
\item[\rm ({b4.}2)] Consider the set
\[
\Gamma:={\lambda}eft\{ \frac{G_{j-1}(z)}{\normaR{G_{j-1}(z)}}\;{{\theta}t b}ig|\;
z\in\varpi_j\;,\;|g_{j-1}(z)|\neq 1 {\rm i}ght\}\;.
\]
Denote by $\Gamma^+$ (resp. $\Gamma^-$) as the part of $\Gamma$
corresponding to $\mathbb{H}^2_+$ (resp. $\mathbb{H}^2_-$). Then, there exists
$p\in\Gamma^+$ so that $\operatorname{dist}_{\mathbb{S}^2}(\pm p,q)<1/{\sigma}qrt{N},$ for
all $q\in \Gamma^\pm.$
\end{enumerate}
\item There exists an orthonormal frame $S_j=\{e_1,e_2,e_3\}$ in
$\mathbb{L}^3,$ where $e_3\in \mathbb{H}^2_+$ and the following assertions hold.
{{\theta}t b}egin{enumerate}[\rm ({b5}.1)]
\item $\operatorname{dist}_{\mathbb{H}^2_+}(e_3,\mathbb{N}N(X(z))){\lambda}eq
{\tt const}/{\sigma}qrt{N},$ for all $z\in \varpi_j.$
\item $\operatorname{dist}_{\mathbb{H}^2_+}(e_3,\pm q){\gamma}eq {\tt const}/{\sigma}qrt{N}$ and $\operatorname{dist}_{\mathbb{H}^2_-}(-e_3,\pm q){\gamma}eq
{\tt const}/{\sigma}qrt{N},$ for any $q$ in the set
$\{G_{j-1}(z)\;|\;z\in\varpi_j,\;|g_{j-1}(z)|\neq 1\}.$ We mean
that we only have to compute the distance if both points are in
the same connected component of $\mathbb{H}^2.$
\end{enumerate}
\end{enumerate}
\end{claim}
{{\theta}t b}egin{proof}
To deduce (b1) and (b2) we have to use just (a2$_k$),
$k=1,{\lambda}dots,j-1.$ Item (b3) is a consequence of (b1) and Claim
\ref{cla: abcd}.A. In order to prove (b4) we distinguish cases. If
$j\in I_0,$ taking into account Claim \ref{cla: abcd}.A and Claim
\ref{cla: abcd}.C we obtain that the diameter of $G_0(\varpi_j)$
is bounded by ${\tt const}/N.$ Then, we can apply (a5.1$_k$),
$k=1,{\lambda}dots,j-1,$ to conclude (b4.1). On the other hand, if $j\in
J_0,$ we use again Claim \ref{cla: abcd}.A and Claim \ref{cla:
abcd}.C to deduce that $\operatorname{diam}_\mathbb{C}(g_0(\varpi_j))<{\tt const}/N.$
Therefore, (a5.2$_k$), $k=1,{\lambda}dots,j-1,$ imply that
$\operatorname{diam}_\mathbb{C}(g_{j-1}(\varpi_j))<{\tt const}/N.$ This fact guarantees (b4.2)
for a large enough $N.$ We also have taken into account that if
$|g_{i-1}(z)|<1<|g_{i-1}(z')|$ and $g_{i-1}(z){\alpha}pprox
g_{i-1}(z'),$ then $G_{j-1}(z) {\alpha}pprox -G_{j-1}(z').$
The proof of (b5) is slightly more complicated. First, assume that
$j\in I_0.$ Without loss of generality we can assume that
$G_{j-1}(\varpi_j){\sigma}ubset \mathbb{H}_+^2,$ otherwise we would work with
$-G_{j-1}(\varpi_j).$ Consider $p$ given by Property (b4.1), then
to obtain (b5.2), it suffices to take $e_3$ in
$C=\{q\in\mathbb{H}^2_+\;|\;\operatorname{dist}_{\mathbb{H}^2_+}(p,q)>2/{\sigma}qrt{N}\}.$ Moreover,
in order to satisfy (b5.1), the vector $e_3$ must be chosen as
follows.
{{\theta}t b}egin{itemize}
\item If $C\cap \mathbb{N}N(X(\varpi_j))\neq \emptyset,$ then we take
$e_3$ in that set. Therefore (b5.1) holds because of Claim
\ref{cla: abcd}.B.
\item If $C\cap \mathbb{N}N(X(\varpi_j))= \emptyset,$ then we take
$e_3\in C$ such that $\operatorname{dist}_{\mathbb{H}^2_+}(e_3,q')<2/{\sigma}qrt{N}$ for some
$q'\in \mathbb{N}N(X(\varpi_j)).$ This choice is possible since (b4.1).
Again Claim \ref{cla: abcd}.B. guarantees (b5.1).
\end{itemize}
Assume now that $j\in J_0.$ We define the sets
\[
\mathbb{L}ambda_\pm:={\lambda}eft\{\frac{q}{\normaR{q}}\;{{\theta}t b}ig|\;q\in\mathbb{H}^2_\pm{\rm i}ght\}{\sigma}ubset\mathbb{S}^2\;,\quad
\Xi:={\lambda}eft\{ \frac{\mathbb{N}N(X(z))}{\normaR{\mathbb{N}N(X(z))}}
\;{{\theta}t b}ig|\;z\in\varpi_j{\rm i}ght\}{\sigma}ubset\mathbb{L}ambda_+\;.
\]
In order to prove assertion (b5) in this case, we are going to use
the following statement. There exists $e_3\in \mathbb{H}^2_+$ so that the
vector $\widehat{e}_3=e_3/\normaR{e_3}$ satisfies
{{\theta}t b}egin{enumerate}[ i)]
\item $\operatorname{dist}_{\mathbb{L}ambda_+}(\widehat{e}_3,q){\lambda}eq {\tt const}/{\sigma}qrt{N},$ for all
$q\in \Xi.$
\item $\operatorname{dist}_{\mathbb{L}ambda_+}(\widehat{e}_3,\pm q){\gamma}eq {\tt const}/{\sigma}qrt{N}$ and
$\operatorname{dist}_{\mathbb{L}ambda_-}(-\widehat{e}_3,\pm q){\gamma}eq {\tt const}/{\sigma}qrt{N}$ for
any $q\in\Gamma.$ Again, we mean that we only have to compute the
distance if both points are in $\mathbb{L}ambda_+$ or both in $\mathbb{L}ambda_-.$
\end{enumerate}
Indeed, the proof consists of the same arguments as above but
using (b4.2) instead of (b4.1). Then, (b5.1) is a consequence of
i) and the fact that $\normaR{\mathbb{N}N(X(\varpi_j))}$ is bounded (not
depending on $N$). Moreover, ii) implies (b5.2). Hence, $e_3$
proves Property (b5) in this case.
\end{proof}
Now, we can continue with the proof of Claim \ref{cla: 5.2}. Let
$(g^{j-1},\phi_3^{j-1})$ be the Weierstrass data of the immersion
$F_{j-1}$ in the basis $S_j$ given by (b5). For any ${\alpha}>0,$
consider $h_{\alpha}:\overline{\operatorname{Int} P}{\theta}o\mathbb{C}$ a holomorphic function
without zeros and satisfying
{{\theta}t b}egin{itemize}
\item $|h_{\alpha}-1|<1/{\alpha}$ in $\overline{\operatorname{Int} P}{\sigma}etminus \varpi_j.$
\item $|h_{\alpha}-{\alpha}|<1/{\alpha}$ in ${\omega}_j.$
\end{itemize}
This family of functions is given by Runge's Theorem. Using $h_{\alpha}$
as a López-Ros parameter, we define $F_j$ in the coordinate system
$S_j$ as $g^j=g^{j-1}/h_{\alpha}$ and $\phi_3^j=\phi_3^{j-1}.$ Taking
into account that $h_{\alpha}{\theta}o 1$ (resp. $h_{\alpha}{\theta}o\infty$) uniformly in
$\overline{\operatorname{Int} P}{\sigma}etminus \varpi_j$ (resp. in ${\omega}_j$), as
${\alpha}{\theta}o\infty,$ it is clear that Properties (a1$_j$), (a2$_j$),
(a3$_j$), (a5$_j$) and (a7$_j$) hold for a large enough (in terms
of $N$) value of the parameter ${\alpha}.$ Moreover, using (b5.1) we
obtain (a6.1$_j$) and to get (a6.2$_j$) we use that
$\phi_3^{j-1}=\phi_3^j$ in the frame $S_j.$ Finally, we are going
to prove (a4$_j$). Consider $z\in\varpi_j$ with $|g^{j-1}(z)|\neq
1.$ Using the stereographic projection for $\mathbb{H}^2$ from the point
$e_3\in\mathbb{H}^2_+,$ from Property (b5.2) one has
\[
\frac{{\sigma}inh {{\theta}t b}ig(\frac{{\tt const}}{{\sigma}qrt{N}}{{\theta}t b}ig)}{\cosh
{{\theta}t b}ig(\frac{{\tt const}}{{\sigma}qrt{N}}{{\theta}t b}ig)+1}{\lambda}eq |g^{j-1}(z)|{\lambda}eq
\frac{{\sigma}inh {{\theta}t b}ig(\frac{{\tt const}}{{\sigma}qrt{N}}{{\theta}t b}ig)}{\cosh
{{\theta}t b}ig(\frac{{\tt const}}{{\sigma}qrt{N}}{{\theta}t b}ig)-1}\;.
\]
On the other hand, if $|g^{j-1}(z)|=1,$ then the above
inequalities trivially hold, so they occur for any $z\in\varpi_j.$
Therefore,
\[
\normaR{\phi^j} {\gamma}eq |\phi_3^j|=|\phi_3^{j-1}|{\gamma}eq {\sigma}qrt{2}
\normaR{\phi^{j-1}}\frac{|g^{j-1}|}{1+|g^{j-1}|^2}
\]
\[
{\gamma}eq {\tt const} \cdot {\theta}anh {\lambda}eft(\frac{{\tt const}}{{\sigma}qrt{N}}{\rm i}ght){\gamma}eq
\frac{{\tt const}}{{\sigma}qrt{N}}\quad {\theta}ext{in }\varpi_j\;,
\]
where we have used (a6.2$_j$) and (b2). This fact proves (a4$_j$)
and concludes the proof of Claim \ref{cla: 5.2}.
\end{proof}
{{\theta}t b}egin{remark}
Notice that in the definition of $F_i$ in Property (a1$_i$), we
need the addition of the fixed vector $V.$ Otherwise, it would be
$F_i(0)=(0,0,0).$ In particular, $X(0)=(0,0,0)\notin {{\theta}t B}(r),$ which
is absurd.
\end{remark}
{{\theta}t b}egin{remark}{\lambda}abel{rem: ortonormal}
Let $S_i=\{e_1,e_2,e_3\}$ be the $\mathbb{L}^3$-orthonormal basis given by
Property (a6$_i$). Consider
$\widetilde{S}_i=\{\widetilde{e}_1,\widetilde{e}_2,\widetilde{e}_3\}$
an $\mathbb{R}^3$-orthonormal basis such that $\{e_1,e_2\}$ and
$\{\widetilde{e}_1,\widetilde{e}_2\}$ define the same plane, and
$e_3$ and $\widetilde{e}_3$ lie in the same halfspace determined
by that plane, i.e.,
$\widetilde{e}_3=-\mathcal{J}(e_3)/\normaR{e_3},$ where
$\mathcal{J}(e_3^1,e_3^2,e_3^3)=(e_3^1,e_3^2,-e_3^3).$ Then, one
has
{{\theta}t b}egin{itemize}
\item
$\operatorname{dist}_{\mathbb{S}^2}(\widetilde{e}_3,\mathbb{N}N_0(X(z)))<{\tt const}/{\sigma}qrt{N},$ for
any $z\in\varpi_i,$ where $\mathbb{N}N_0$ is the map that was defined in
page \pageref{pag: normales}.
\item $(F_i(z))_{(3,\widetilde{S}_i)}=
(F_{i-1}(z))_{(3,\widetilde{S}_i)}.$
\end{itemize}
\end{remark}
Now, we establish some properties of the final immersion $F_{2N}.$
{{\theta}t b}egin{claim}{\lambda}abel{cla: final}
If $N$ is large enough, then $F_{2N}$ satisfies
{{\theta}t b}egin{enumerate}[\rm ({c}1)]
\item $2s < \operatorname{dist}_{(\overline{\operatorname{Int}
P}\,,\,d{\sigma}igma_{F_{2N}})}(P,P^{\epsilon}),$ where by $d{\sigma}igma_{F_{2N}}$
we represent the lift metric of the immersion $F_{2N}.$
\item $\normaR{F_{2N}-X}<{\tt const}/N,$ in $\overline{\operatorname{Int} P}{\sigma}etminus
(\cup_{i=1}^{2N} \varpi_i).$
\item There exists a polygon $Q$ such that
{{\theta}t b}egin{enumerate}[\rm ({c3}.1)]
\item $\overline{\operatorname{Int} P^{\epsilon}} {\sigma}ubset \operatorname{Int} Q {\sigma}ubset
\overline{\operatorname{Int} Q}{\sigma}ubset \operatorname{Int} P.$
\item $s<\operatorname{dist}_{(\overline{\operatorname{Int} P}\,,\,
d{\sigma}igma_{F_{2N}})}(z,P^{\epsilon})<2s,$ for any $z\in Q.$
\item $F_{2N}(\overline{\operatorname{Int} Q}){\sigma}ubset {{\theta}t B}(R),$
where $R={\sigma}qrt{r^2-4s^2}-{\epsilon}.$
\end{enumerate}
\end{enumerate}
\end{claim}
{{\theta}t b}egin{proof}
Properties (b2), (a2$_i$), (a3$_i$) and (a4$_i$), $i=1,{\lambda}dots,2N,$
guarantee that the conformal coefficient ${\lambda}_{F_{2N}}^0$ of the
lift metric of $F_{2N}$ satisfies
\[
{\lambda}_{F_{2N}}^0 =\frac{\normaR{\phi^{2N}}}{{\sigma}qrt{2}}{\gamma}eq
{{\theta}t b}egin{cases}
\frac{{\tt const}}{{\sigma}qrt{N}} & {\theta}ext{in }\operatorname{Int} P\\
\frac{{\tt const}}{{\sigma}qrt{N}}\, N^4 & {\theta}ext{in }{\Omega}ega_N\;.
\end{cases}
\]
Therefore, Claim \ref{cla: abcd}.D imply that
\[
\operatorname{dist}_{(\overline{\operatorname{Int} P}\,,\,d{\sigma}igma_{F_{2N}})}(P,P^{\epsilon}){\gamma}eq
\operatorname{dist}_{(\overline{\operatorname{Int} P}\,,\,d{\sigma}igma_{F_{2N}})}(P,P^{\zeta_0})>
\frac{{\tt const}}{{\sigma}qrt{N}}\,N={\tt const}{\sigma}qrt{N}>2s\;,
\]
for a large enough $N.$ We have proved (c1). Property (c2)
trivially holds from (a2$_i$), $i=1,{\lambda}dots,2N.$
In order to construct the polygon $Q$ of the assertion (c3), we
consider the set
\[
\mathcal{K}={{\theta}t b}ig\{ z\in (\operatorname{Int} P){\sigma}etminus (\operatorname{Int} P^{\epsilon})\;{{\theta}t b}ig|\;
s< \operatorname{dist}_{(\overline{\operatorname{Int} P}\,,\,d{\sigma}igma_{F_{2N}})}(z,P^{\epsilon})<2s
{{\theta}t b}ig\}\;.
\]
From (c1), $\mathcal{K}$ is a nonempty open subset of $(\operatorname{Int}
P){\sigma}etminus (\operatorname{Int} P^{\epsilon}),$ and $P$ and $P^{\epsilon}$ are contained in
different connected components of $\mathbb{C}{\sigma}etminus\mathcal{K}.$
Therefore, we can choose a polygon $Q$ on $\mathcal{K}$ satisfying
(c3.1) and (c3.2).
The proof of (c3.3) is more complicated. Consider
$z\in\overline{\operatorname{Int} Q}.$ First, we assume that $z\in (\operatorname{Int}
P){\sigma}etminus (\cup_{i=1}^{2N}\varpi_i).$ Then, we can use
Properties (a2$_i$), $i=1,{\lambda}dots,2N,$ to conclude that
$\normaR{F_{2N}(z)-X(z)}<{\tt const}/N.$ Moreover, from the hypotheses of
Lemma \ref{lema}, we have $X(z)\in {{\theta}t B}(r).$ Hence, $F_{2N}(z)\in
{{\theta}t B}(R),$ if $N$ is large enough.
On the other hand, suppose that there exists $i\in
\{1,{\lambda}dots,2N\}$ with $z\in\varpi_i.$ Choose a curve ${\gamma}:[0,1]{\theta}o
\operatorname{Int} P$ satisfying ${\gamma}(0)\in P^{\epsilon},$ ${\gamma}(1)=z$ and
$\operatorname{length}({\gamma},d{\sigma}igma_{F_{2N}})< 2s.$ This election is possible
since (c3.2). Label
\[
t_0={\sigma}up{{\theta}t b}ig\{ t\in[0,1]\;{{\theta}t b}ig|\; {\gamma}(t)\in\partial
\varpi_i{{\theta}t b}ig\}\;,\quad z_0={\gamma}(t_0)\;.
\]
Notice that this supremum exists because $\varpi_i{\sigma}ubset (\operatorname{Int}
P){\sigma}etminus \overline{\operatorname{Int} P^{\epsilon}}$ (for a large enough $N$). Now,
consider the basis $\widetilde{S}_i$ explained in Remark \ref{rem:
ortonormal}, then we have
{{\theta}t b}egin{equation}{\lambda}abel{ecu: pita12}
\norma{(F_{2N}(z)-X(z))_{(*,\widetilde{S}_i)}}{\lambda}eq
2s+\frac{{\tt const}}{{\sigma}qrt{N}}\;,
\end{equation}
{{\theta}t b}egin{equation}{\lambda}abel{ecu: pita3}
|(F_{2N}(z)-X(z))_{(3,\widetilde{S}_i)}|<\frac{{\tt const}}N\;.
\end{equation}
{{\theta}t b}egin{figure}[htbp]
{{\theta}t b}egin{center}
\includegraphics[width=0.50{\theta}extwidth]{dibujo.eps}
\end{center}
\caption{The effect of the deformation.}{\lambda}abel{fig: 2}
\end{figure}
Indeed,
\[
\norma{(F_{2N}(z)-X(z))_{(*,\widetilde{S}_i)}}{\lambda}eq\normaR{F_{2N}(z)-F_{2N}(z_0)}+
\normaR{F_{2N}(z_0)-F_{i-1}(z_0)}+
\]
\[
\normaR{F_{i-1}(z_0)-F_{i-1}(z)}+\normaR{F_{i-1}(z)-X(z)}{\lambda}eq
\]
\[
\operatorname{length}({\gamma},d{\sigma}igma_{F_{2N}})+\frac{{\tt const}}N+\frac1{{\sigma}qrt{N}}+\frac{{\tt const}}N<2s+\frac{{\tt const}}{{\sigma}qrt{N}}\;,
\]
where we have used (a7$_j$), $j=1,{\lambda}dots,2N,$ and (b3). On the
other hand, taking Remark \ref{rem: ortonormal} and (a7$_j$),
$j=1,{\lambda}dots,2N,$ into account, we conclude
\[
|(F_{2N}(z)-X(z))_{(3,\widetilde{S}_i)}|{\lambda}eq
\normaR{F_{2N}(z)-F_i(z)}+
|(F_{i}(z)-F_{i-1}(z))_{(3,\widetilde{S}_i)}|+
\]
\[
\normaR{F_{i-1}(z)-X(z)}<\frac{{\tt const}}N+\frac{{\tt const}}N=\frac{{\tt const}}N\;.
\]
At this point, consider the following statement. Its proof is
elemental, we leave the details to the reader.
{{\theta}t b}egin{claim}{\lambda}abel{cla: bolas}
Let $0<x<t.$ Consider $p\in {{\theta}t B}(t)$ and $v\in\mathbb{R}^3$ with
$\escproR{\mathbb{N}N_0(p),v}=0$ and $\normaR{v}=x.$ Then, $p+v\in
{{\theta}t B}({\sigma}qrt{t^2-x^2}).$
\end{claim}
Now, Remark \ref{rem: ortonormal}, equations \eqref{ecu: X-cota},
\eqref{ecu: pita12} and \eqref{ecu: pita3}, and the above claim
guarantee that $F_{2N}(z)\in {{\theta}t B}(R),$ if $N$ was chosen large
enough. This proves (c3.3) and finishes the proof of Claim
\ref{cla: final}.
\end{proof}
From Claim \ref{cla: final} it is straightforward to check that
(for $N$ large enough) $Y=F_{2N}:\overline{\operatorname{Int} Q}{\theta}o\mathbb{L}^3$ proves
Lemma \ref{lema}.
{{\theta}t b}egin{thebibliography}{99}
{{\theta}t b}ibitem{dga} A. Alarcón, {\em On the existence of a proper
conformal maximal disk in $\mathbb{L}^3.$} To appear in Differ. Geom.
Appl.
{{\theta}t b}ibitem{salvador} A. Alarcón, {\em Recent progresses in the
Calabi-Yau problem for minimal surfaces.} To appear in Mat.
Contemp.
{{\theta}t b}ibitem{yo-isa} A. Alarcón, {\em The convex
hull property and the Calabi-Yau problem for maximal surfaces.} In
preparation.
{{\theta}t b}ibitem{AFM} A. Alarcón, L. Ferrer and F. Martín, {\em Density
theorems for complete minimal surfaces in $\mathbb{R}^3.$}
To appear in Geom. Funct. Anal.
{{\theta}t b}ibitem{Calabi} E. Calabi, {\em Examples of the Bernstein problem
for some nonlinear equations.} Proc. Symp. Pure Math., {{{\theta}t b}f 15} (1970), 223-230.
{{\theta}t b}ibitem{leo-rosa} R. Chaves and L. Ferrer, {\em Nonexistence results
and convex hull property for maximal surfaces in Minkowski
three-space.} Pac. J. Math., {{{\theta}t b}f 231} (2007), 1-26.
{{\theta}t b}ibitem{Ch-Yau} S. Y. Cheng and S. T. Yau, {\em Maximal space-like
hypersurfaces in the Lorentz-Minkowski spaces.} Annals of Math., {{{\theta}t b}f 104} (1976), 407-419.
{{\theta}t b}ibitem{Isa-PL1} I. Fernández and F. J. López, {\em Periodic
maximal surfaces in the Lorentz-Minkowski space $\mathbb{L}^3$.} Math. Z.,
{{{\theta}t b}f 256} (2007), 573-601.
{{\theta}t b}ibitem{Isa-PL2} I. Fernández and F. J. López, {\em The uniqueness
of the helicoid in the Lorentz-Minkowski space $\mathbb{L}^3.$} Preprint.
{{\theta}t b}ibitem{Isa-PL-RS} I. Fernández, F. J. López and R. Souam, {\em The
space of complete embedded maximal surfaces with isolated singularities
in the 3-dimensional Lorentz-Minkowski space $\mathbb{L}^3$.} Math. Ann., {{{\theta}t b}f 332} (2005), 605-643.
{{\theta}t b}ibitem{FSUY} S. Fujimori, K. Saji, M. Umehara and K. Yamada,
{\em Singularities of maximal surfaces.} To appear in Math. Z.
{{\theta}t b}ibitem{Kiehn} R. M. Kiehn, {\em Falaco Solitons. Cosmic
strings in a swimming pool.} http:/www22.pair.com/csdc/pdf/falsol.pdf
{{\theta}t b}ibitem{Kiehn2} R. M. Kiehn, {\em Experimental Evidence
for Maximal Surfaces in a 3 Dimensional Minkowski Space.}
http://www22.pair.com/csdc/download/maxsurf.pdf
{{\theta}t b}ibitem{Koba0} O. Kobayashi, {\em Maximal surfaces in the
3-dimensional Minkowski space $\mathbb{L}^3$.} Tokyo J. Math., {{{\theta}t b}f 6} (1983), 297-309.
{{\theta}t b}ibitem{Koba} O. Kobayashi, {\em Maximal surfaces with
conelike singularities.} J. Math. Soc. Japan, {{{\theta}t b}f 36} (1984), 609-617.
{{\theta}t b}ibitem{LLS} F. J. López, R. López and R. Souam, {\em Maximal
surfaces of Riemann type in Lorentz-Minkowsky space $\mathbb{L}^3$.}
Michigan Math. J. {{{\theta}t b}f 47} (2000), 469-497.
{{\theta}t b}ibitem{MT} J. E. Marsden and F. J. Tipler., {\em Maximal
hypersurfaces and foliations of constant mean curvature in general
relativity.} Phys. Rep., {{{\theta}t b}f 66} (1980), 109-139.
{{\theta}t b}ibitem{MM-Convex} F. Martín and S. Morales, {\em Complete proper
minimal surfaces in convex bodies of $\mathbb{R}^3$.}
Duke Math. J., {{{\theta}t b}f 128} (2005), 559-593.
{{\theta}t b}ibitem{MM-Convex2} F. Martín and S. Morales, {\em Complete proper
minimal surfaces in convex bodies of $\mathbb{R}^3$ (II):
The behavior of the limit set.} Comment. Math. Helv., {{{\theta}t b}f 81}
(2006), 699-725.
{{\theta}t b}ibitem{MN} F. Martín and N. Nadirashvili, {\em A Jordan curve
spanned by a complete minimal surface.} Arch. Ration. Mech. An.
{{{\theta}t b}f 184} (2007), 285-301.
{{\theta}t b}ibitem{nadi} N. Nadirashvili, {\em Hadamard's and Calabi-Yau's
conjectures on negatively curved and minimal surfaces.} Invent.
Math. {{{\theta}t b}f 125} (1996), 457-465.
{{\theta}t b}ibitem{osserman} R. Osserman, {\em A survey of minimal
surfaces.} Dover Publications, New York (1986).
{{\theta}t b}ibitem{Um-Ya} M. Umehara and K. Yamada, {\em Maximal
surfaces with singularities in Minkowski space.}
Hokkaido Math. J., {{{\theta}t b}f 35} (2006), 13-40.
\end{thebibliography}
\end{document}
\end{document} | math |
رِسؠپشنِسٹ | kashmiri |
Purple is a royal color beloved by kings, emperors, queens, and other leaders and rulers for its rarity and beauty. Now you can get wonderful discount choir robes and robe stoles for kids and adults, all in eye-catching purple shades! Robes are available in both smooth, warm matte material, as well as shimmering shiny material. Save time and money when you shop at DiscountChoirRobes.com! | english |
If you are starting or restructuring a business, you will no doubt want to know how to get through the process with as few problems as possible. At Ric Blackwell Law, we help business owners of all ages with the creation and operation of companies that generate millions of dollars in revenues. We have particular expertise working with technology companies. We advise our clients on any issues that arise in the course of managing the business, including business formation and organization, corporate structure, partnerships, financial planning, negotiations, mergers and acquisitions, and liability issues, helping them to understand potential risks and make the decisions that are best for their companies.
Many factors determine whether a succession plan is necessary, and sometimes the logical and easy choice will be to simply sell the business lock, stock and barrel. However, many owners prefer the thought of their businesses continuing on even after they’re gone.
Choosing a successor can be as easy as appointing a family member or assistant to take the owner’s place. However, there may be several partners or family members from which the owner will have to choose — each with a number of strengths and weaknesses to be considered. In this case, a lasting resentment by those who were not chosen may happen, regardless of what choice is ultimately made. Partners who do not need or want a successor may simply sell their portion of the business to the other partners of the business in a buy-sell agreement. | english |
/* -*- Mode:C++; c-file-style:"gnu"; indent-tabs-mode:nil; -*- */
/**
* Copyright (c) 2014, Regents of the University of California,
* Arizona Board of Regents,
* Colorado State University,
* University Pierre & Marie Curie, Sorbonne University,
* Washington University in St. Louis,
* Beijing Institute of Technology,
* The University of Memphis
*
* This file is part of NFD (Named Data Networking Forwarding Daemon).
* See AUTHORS.md for complete list of NFD authors and contributors.
*
* NFD is free software: you can redistribute it and/or modify it under the terms
* of the GNU General Public License as published by the Free Software Foundation,
* either version 3 of the License, or (at your option) any later version.
*
* NFD is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY;
* without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR
* PURPOSE. See the GNU General Public License for more details.
*
* You should have received a copy of the GNU General Public License along with
* NFD, e.g., in COPYING.md file. If not, see <http://www.gnu.org/licenses/>.
*/
#ifndef NFD_DAEMON_FACE_UDP_CHANNEL_HPP
#define NFD_DAEMON_FACE_UDP_CHANNEL_HPP
#include "channel.hpp"
#include "core/global-io.hpp"
#include "udp-face.hpp"
namespace nfd {
namespace udp {
typedef boost::asio::ip::udp::endpoint Endpoint;
} // namespace udp
/**
* \brief Class implementing UDP-based channel to create faces
*
*
*/
class UdpChannel : public Channel
{
public:
/**
* \brief Exception of UdpChannel
*/
struct Error : public std::runtime_error
{
Error(const std::string& what) : runtime_error(what) {}
};
/**
* \brief Create UDP channel for the local endpoint
*
* To enable creation of faces upon incoming connections,
* one needs to explicitly call UdpChannel::listen method.
* The created socket is bound to the localEndpoint.
* reuse_address option is set
*
* \throw UdpChannel::Error if bind on the socket fails
*/
UdpChannel(const udp::Endpoint& localEndpoint,
const time::seconds& timeout);
/**
* \brief Enable listening on the local endpoint, accept connections,
* and create faces when remote host makes a connection
* \param onFaceCreated Callback to notify successful creation of the face
* \param onAcceptFailed Callback to notify when channel fails
*
* Once a face is created, if it doesn't send/receive anything for
* a period of time equal to timeout, it will be destroyed
* \todo this functionality has to be implemented
*
* \throws UdpChannel::Error if called multiple times
*/
void
listen(const FaceCreatedCallback& onFaceCreated,
const ConnectFailedCallback& onAcceptFailed);
/**
* \brief Create a face by establishing connection to remote endpoint
*
* \throw UdpChannel::Error if bind or connect on the socket fail
*/
void
connect(const udp::Endpoint& remoteEndpoint,
const FaceCreatedCallback& onFaceCreated,
const ConnectFailedCallback& onConnectFailed);
/**
* \brief Create a face by establishing connection to the specified
* remote host and remote port
*
* This method will never block and will return immediately. All
* necessary hostname and port resolution and connection will happen
* in asynchronous mode.
*
* If connection cannot be established within specified timeout, it
* will be aborted.
*/
void
connect(const std::string& remoteHost, const std::string& remotePort,
const FaceCreatedCallback& onFaceCreated,
const ConnectFailedCallback& onConnectFailed);
/**
* \brief Get number of faces in the channel
*/
size_t
size() const;
private:
shared_ptr<UdpFace>
createFace(const shared_ptr<boost::asio::ip::udp::socket>& socket,
const FaceCreatedCallback& onFaceCreated,
bool isOnDemand);
void
afterFaceFailed(udp::Endpoint& endpoint);
/**
* \brief The UdpChannel has received a new pkt from a remote endpoint not yet
* associated with any UdpFace
*/
void
newPeer(const boost::system::error_code& error, size_t nBytesReceived);
void
handleEndpointResolution(const boost::system::error_code& error,
boost::asio::ip::udp::resolver::iterator remoteEndpoint,
const FaceCreatedCallback& onFaceCreated,
const ConnectFailedCallback& onConnectFailed,
const shared_ptr<boost::asio::ip::udp::resolver>& resolver);
private:
udp::Endpoint m_localEndpoint;
/**
* \brief Endpoint used to store the information about the last new remote endpoint
*/
udp::Endpoint m_newRemoteEndpoint;
/**
* Callbacks for face creation.
* New communications are detected using async_receive_from.
* Its handler has a fixed signature. No space for the face callback
*/
FaceCreatedCallback onFaceCreatedNewPeerCallback;
// @todo remove the onConnectFailedNewPeerCallback if it remains unused
ConnectFailedCallback onConnectFailedNewPeerCallback;
/**
* \brief Socket used to "accept" new communication
**/
shared_ptr<boost::asio::ip::udp::socket> m_socket;
uint8_t m_inputBuffer[MAX_NDN_PACKET_SIZE];
typedef std::map< udp::Endpoint, shared_ptr<UdpFace> > ChannelFaceMap;
ChannelFaceMap m_channelFaces;
/**
* \brief If true, it means the function listen has already been called
*/
bool m_isListening;
/**
* \brief every time m_idleFaceTimeout expires all the idle (and on-demand)
* faces will be removed
*/
time::seconds m_idleFaceTimeout;
};
} // namespace nfd
#endif // NFD_DAEMON_FACE_UDP_CHANNEL_HPP
| code |
ये कंपनी दे रही है मात्र २९९ रुपये में अनलिमिटेड कॉल व डेटा बैलेंस
कंपनी ने बुधवार को एक ट्वीट कर इस नए प्लान की जानकारी दी कंपनी ने कहा, रिलायंस मोबाइल ने अब तक का सबसे सस्ता प्लान पेश किया है! २९९ रुपये प्रतिमाह की दर पर.
रिलायंस कम्युनिकेशन्स के नए लेटेस्ट रेंटल प्लान को एयरटेल, वोडाफोन और जियो जैसी दिग्गज़ कंपनियों को टक्कर देने के लिए पेश किया है. टीज़र से पुष्टि होती है कि २९९ रुपये वाले प्लान के तहत, आरकॉम यूज़र को अनलिमिटेड कॉल, टेक्स्ट और डेटा मिलेगा.
बता दें कि, अनिल अंबानी के नेतृत्व वाली आरकॉम को दूसरी घरेलू कंपनियों से मिल रही कड़ी चुनौती के चलते संघर्ष करना पड़ रहा है. अनिल अंबानी की रिलायंस कम्युनिकेशंस के शेयर और बॉन्ड में इसी साल मई में कमी देखी गई, और इसके लिए अप्रत्यक्ष तौर पर मुकेश अंबानी की रिलायंस जियो द्वारा दी जा रहीं 'मुफ्त सेवाओं' को जिम्मेदार ठहराया गया. | hindi |
अंतरिक्ष में भी उगते हैं फूल और सब्जियां
यह है जीनिया. अंतरराष्ट्रीय स्पेस स्टेशन आईएसएस पर खिला पहला फूल. जीनिया को खाया भी जा सकता है. इसे उगाने का मकसद भी अंतरिक्ष यान की खूबसूरती बढ़ाना नहीं, बल्कि अंतरिक्ष में यात्रियों का पेट भरना है. इस तस्वीर को अंतरिक्ष यात्री स्कॉट केली ने ट्वीट किया.
२३ अक्टूबर २०१५ को स्कॉट केली अंतरिक्ष में सबसे लंबा वक्त बिताने वाले इंसान बन गए. तब तक वे स्पेस में ३८२ दिन बिता चुके थे. फिलहाल वे अमेरिकी अंतरिक्ष एजेंसी नासा के "वन ईयर मिशन" के कप्तान हैं और लगातार अंतरिक्ष से तस्वीरें ट्वीट करते हैं.
वन ईयर मिशन
मार्च २०१५ से अमेरिका के स्कॉट केली और रूस के मिखाइल कोरनीएंको नासा के वन ईयर मिशन का हिस्सा हैं. मकसद है आईएसएस पर रह कर अंतरिक्ष यात्रियों की मानसिक और शारीरिक सेहत पर पड़ने वाले असर का अध्ययन करना.
अंतरिक्ष यात्रियों को खुद अपने लिए खाना भी उगाना है. इस प्रोजेक्ट को नासा ने वेजिटेबल प्रोडक्शन सिस्टम का नाम दिया है, जिसे वेजी कहा जाने लगा है. मकसद है ऐसी चीजें उगाना जो भविष्य में मंगल पर रहने वाली बस्ती के काम आ सकें.
अंतरिक्ष में पौधों को बिना मिट्टी के उगाया जाता है. इसमें बहुत कम पानी और खाद खर्च होती है. इस तरीके को एयरोपॉनिक्स कहा जाता है. इसमें पौधे सामान्य से तीन गुना ज्यादा तेजी से बढ़ते हैं.
पौधों को अंतरिक्ष में माइक्रोग्रैविटी का सामना करना पड़ता है, इसलिए उन्हें उगाना मुश्किल हो जाता है. जीनिया के पौधे पर ज्यादा नमी के कारण फफूंद लग गयी थी लेकिन केली उसे बचाने में कामयाब रहे.
२०१४ में आईएसएस पर पौधे उगाने का सिलसिला शुरू हुआ. २०१५ में क्रू ने पहली बार सलाद उगा कर चखा (तस्वीर में). इससे पहले २०१२ में अंतरिक्ष यात्री डॉनल्ड पेटिट ने जुकीनी (एक तरह की लौकी) का पौधा भी उगाया.
नासा की लिस्ट पर अगली सब्जी है चीनी बंद गोभी. इसके बाद २०१८ में आईएसएस पर टमाटर उगाने की भी योजना है. साथ ही सलाद के पत्तों को बेहतर बनाना है. ये सब पौधे छोटे छोटे ग्रीनहाउस में उगाए जाएंगे.
२०१५ में आई हॉलीवुड की बहुचर्चित फिल्म "मार्शियन" में काफी कुछ वैसा दिखाया गया है, जैसा नासा कर रहा है या फिर करने की योजना रखता है. स्कॉट केली भी खुद अपनी तुलना फिल्म के मुख्य किरदार मार्क वॉटनी से कर चुके हैं.
अंतरिक्ष में उगे पहले फूल ने सब को हैरान कर दिया. लेकिन इस फूल के अलावा भी अंतरिक्ष में काफी कुछ उगाया जा रहा है. जानिए अब तक क्या क्या उगा और कैसे.
कीवर्ड अंतरिक्ष, फूल, विज्ञान, तकनीक, स्पेस, आईएसएस, स्पेस स्टेशन, स्कॉट केली | hindi |
VOX Amplification is currently offering consumer rebates on ToneLab ST and ToneLab EX, members of its ToneLab line of Valvetronix modeling pedals.
VOX Amplification is currently offering consumer rebates on ToneLab ST and ToneLab EX, members of its popular ToneLab line of Valvetronix modeling pedals. From June 1 through June 30, 2012, consumers in the US who purchase a new ToneLab pedal online or in-store from an authorized VOX dealer in the US can receive a $25 rebate (ToneLab ST) or $50 rebate (ToneLab EX).
As with all amps and pedals in the Valvetronix Series, the ToneLab EX and ST rely on a real 12AX7 vacuum tube (valve) to accurately capture the tone quality of a tube-driven amplifier.
The ToneLab EX also offers a personal monitoring system for backstage tweaking, editing and rehearsing - as well as programming - without the need for additional amps or equipment.
For rebate details, please visit: www.voxamps.com/us/promos. For further information about the ToneLab Ex and ToneLab ST, please visit www.voxamps.com/us/pedals. | english |
हिंदू रीतियों के आधार पर किसी भी काम की शुरूआत शुभ मुहूर्त पर ही की जाती है । लेकिन साल में एक दिन ऐसा भी है जिसे सर्वसिद्ध मुहूर्त माना गया है । वो दिन है अक्षय तृतीया, जो कि बैशाख माह की शुक्ल पक्ष की तृतीया तिथि को पड़ती है । इस वर्ष अक्षय तृतीया रविवार २६ अप्रैल को पड़ रही है । ऐसी मान्यता है कि अक्षय तृतीया के दिन बिना पंचांग देखे कोई भी शुभ व मांगलिक कार्य जैसे विवाह, गृह प्रवेश, आभूषणों की खरीददारी अथवा प्रॉपर्टी या बिजनेस में निवेश आदि कार्य किए जा सकते हैं । साथ ही पुराणों के अनुसार अक्षय तृतीया अथवा आखा तीज के दिन किसी भी प्रकार का दान अथवा पूजा भी अक्षय फल प्रदान करती है ।
अक्षय तृतीया के दिन मां विंध्यवासिनी की श्रृंगार आरती कराने का अत्यंत महत्व है । मां विंध्यवासिनी देवी का मंदिर उत्तर प्रदेश के मिर्जापुर जिले में विंध्याचल नामक तीर्थ में स्थित है । ऐसा कहा जाता है कि यह मां जगदम्बा का निवास स्थान है, इसलिए यह एक जाग्रत शक्तिपीठ है जो कि मां दुर्गा के ५१ शक्तिपीठों में से एक है । विंध्यवासिनी मंदिर को लेकर ढेरों मान्यताएं व्याप्त हैं । धर्मराज युधिष्ठिर ने मां विंध्यवासिनी की आराधना की थी, इसके अलावा कंस के वध की भविष्यवाणी करने की भी कथा काफी प्रचलित है ।
आज भी प्रतिदिन मां विंध्यवासिनी की दिन में चार बार आरती होती है । भोर में होने वाली आरती को मंगला आरती, दोपहर में मध्यमान आरती, सायं काल में होने वाली आरती को छोटी आरती व रात्रि में होने वाली आरती को बड़ी आरती कहा जाता है । अक्षय तृतीया के दिन मां विंध्यवासिनी की आरती का हिस्सा बनने के लिए व श्रृंगार दान के लिए हर वर्ष भक्तों की भारी भीड़ उमड़ती है । हालांकि इस वर्ष लॉकडाउन के कारण मंदिर भक्तों के लिए बंद है लेकिन पुजारियों के द्वारा मां विंध्यवासिनी की आरती सम्पन्न कराई जाती है ।
अगर आप भी अक्षय तृतीया के दिन मां विंध्सविनी की सामूहिक आरती का हिस्सा बनना चाहते हैं तो मैज्योतिष.कॉम आपके लिए ला रहा है एक खास मौका । जिसमें आप घर से ही मां विध्यवासिनी की आरती का हिस्सा बन सकते हैं साथ ही श्रृंगार दान का शुभ फल भी प्राप्त कर सकते हैं । यह पूजा मंदिर के पुजारी द्वारा आपके नाम से पूरे विधि-विधान से कराई जाएगी । आरती शुरू होने से पहले पंडित जी द्वारा फोन पर आपका संकल्प कराया जाएगा तथा बाद में आपको प्रसाद भी भेजा जाएगा ।
अक्षय तृतीया के शुभ दिन पर माँ विंध्यवासिनी का श्रृंगार करवाने के लिए अभी क्लिक करे | hindi |
vroksjab
========
simple util stuff
| code |
A package for creating simple yet modern looking charts.
#### Five chart types
- Bar
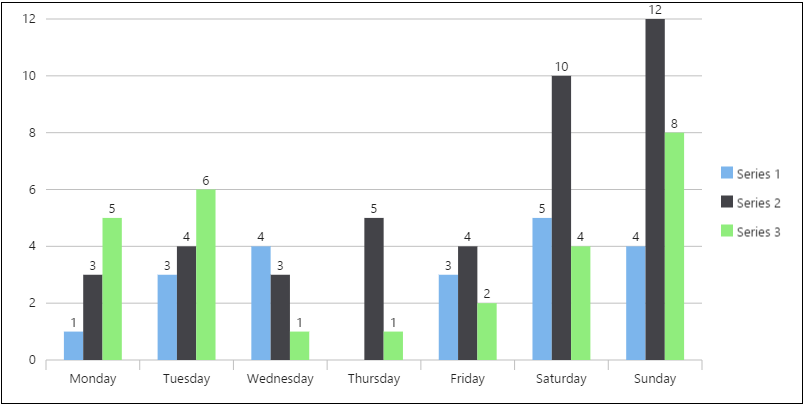
- Gauge
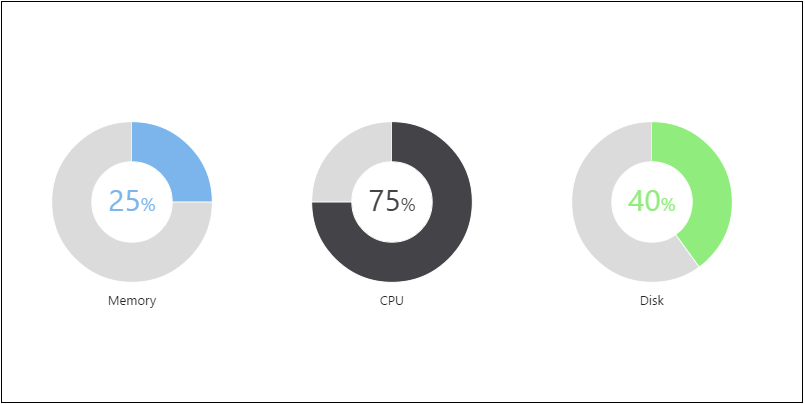
- Line
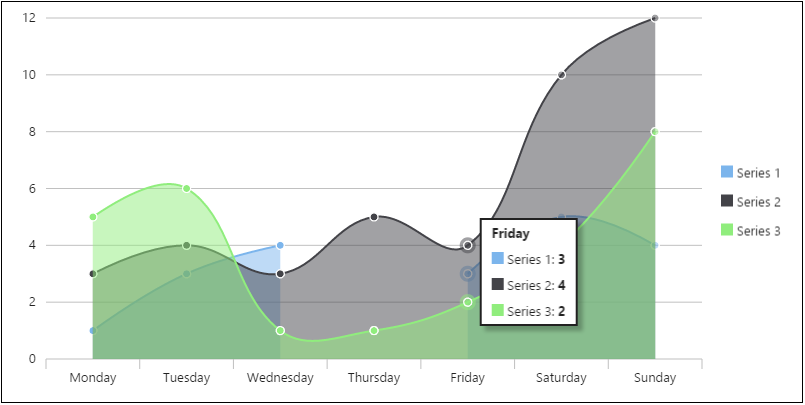
- Pie
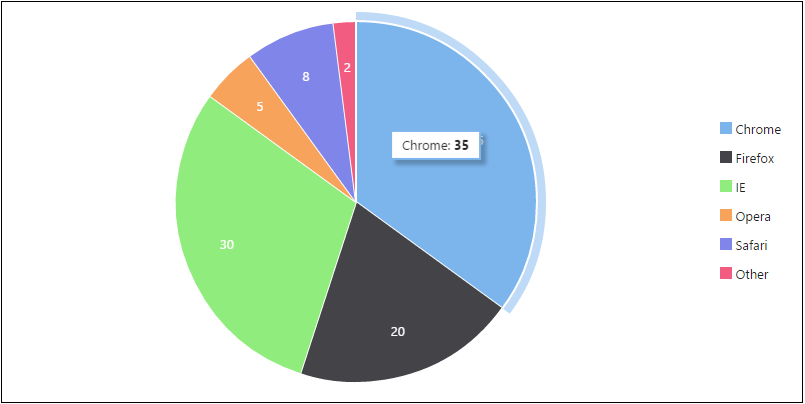
- Radar
#### Canvas + DOM
**modern_charts** combines Canvas and DOM to achieve the best performance and
experience.
- Canvas is used to render chart contents (axes, grids, and series)
- DOM is used to create legends and tooltips
#### DataTable
Data are passed to a chart via a `DataTable` object. By using `DataTable`, you
can flexibly modify the data even after the chart has been rendered.
#### Animations
Animations are supported for different types of data modifications:
- New data table
- Changes to data table values
- Insertion and removal of rows (categories)
- Insertion and removal of columns (series)
- Series visibility toggle
#### Responsive
Charts automatically resize when the browser is resized.
#### Interactive
- Shows tooltips on hover/tap
- The visibility of a series is toggled when you click the corresponding legend
item
#### Modular
Each chart type has its own class, so your final production code only contains
the code of the chart types you use.
#### Usage
Please read the wiki for instructions on how to use these beautiful charts. | code |
आईटीआई कालेज की भूमि का किया सर्वे
बिधूना (औरैया)। अपरजिलाधिकारी लालमणी मिश्रा ने तहसील मुख्यालय स्थित आईटीआई कालेज के निर्माण हेतु भूमि का सर्वे किया। इस दौरान एसडीएम भी मौजूद रहे।
अपर जिलाधिकारी लालमणि मिश्र ने ग्राम रठगांव मौजा की भूमि पर आईटीआई कालेज के लिए भूमि का मौके पर सर्वे किया। इस दौरान उन्हाेंने कानूनगो व क्षेत्रीय लेखपाल को बुलाकर भूमि की जानकारी की तथा नक्शा आदि बनाने के निर्देश दिये। सर्वे के दौरान अपर जिलाधिकारी ने बताया कि प्रदेश के मुख्यमंत्री के निर्देश पर आईटीआई कालेज की भूमि का सर्वे किया जा रहा है। सही भूमि चिंहित होने के बाद रिपोर्ट मुख्यमंत्री को भेजी जायेगी तथा कालेज का निर्माण कार्य भी आरंभ होगा। अपरजिलाधिकारी ने इस मौके पर मौजूद उप जिलाधिकारी अनिल कुमार त्रिपाठी को भी विभागीय निर्देश दिये। | hindi |
- जरूरत ४३ की डाक्टर केवल १३, करनाल न्यूज इन हिन्दी -अमर उजाला बेहतर अनुभव के लिए अपनी सेटिंग्स में जाकर हाई मोड चुनें।
करनाल जरूरत ४३ की डाक्टर केवल १३
कैथल। इंदिरा गांधी मल्टी स्पेशियलिटी अस्पताल के नाम से ही विशेष सुविधाएं होने का बोध होता है। सच्चाई यह है कि अस्पताल इस समय सबसे बड़ी जरूरत डाक्टरों के लिए ही तरस गया है। यहां जरूरत के ४३ डॉक्टरों में से इस समय मात्र १३ डॉक्टर अस्पताल में कार्यरत हैं। इनके भरोसे ओपीडी, आपातकाल विभाग एवं पोस्टमार्टम सहित सभी कार्य रेंग रहे हैं। ऐसे में मरीजोें के साथ-साथ अस्पताल कर्मचारियों एवं चिकित्सकों को भी दिक्कतों का सामना करना पड़ रहा है। पिछले वर्ष शुरू हुए इंदिरा गांधी मल्टी स्पेशियलिटी अस्पताल में कुल ४३ चिकित्सकों के पद हैं। इसमें से जैसे-तैसे करीब छह माह तक चिकित्सकों की संख्या ३० से ऊपर पहुंच गई थी। इस कारण यहां सभी विभागों में ओपीडी मरीजों की संख्या वर्किंग-डे में ६०० से लेकर ७०० तक होती है। कभी यह इससे भी अधिक हो जाती है। चिकित्सक कम होने के बावजूद ओपीडी संख्या लगातार बढ़ रही है। यही अस्पताल में १०० बेड की सुविधा का है। प्रतिदिन १०० के बजाए १२० या १३0 मरीज दाखिल रहते हैं।नाम न छापने की शर्त पर चिकित्सकों ने बताया कि बस काम चल रहा है। नाम मल्टी स्पेशियलिटी अस्पताल है, लेकिन सबसे पहली आवश्यकता चिकित्सक ही नहीं है। इस कारण मरीजाें के साथ-साथ वर्कलोड के चलते उन्हें भी भारी परेशानी हो रही है। अस्पताल में एमबीबीएस चिकित्सकों की काफी कमी है। इस कारण सबसे अधिक परेशानी आपातकाल एवं प्रसूति कक्ष में आ रही है। यहां एक-एक चिकित्सक को डबल शिफ्टों में काम करना पड़ता है। ये है अस्पताल में डाक्टरइस समय अस्पताल में ४३ में से १३ चिकित्सक हैं। इनमें डा. अमन सूद, डा. अनूप, डा. राकेश मित्तल, डा. संदीप सैनी, डा. कविता गोयल, डा. रविंद्र, डा. मीनाक्षी, डा. निधि गर्ग, डा. सुमन, डा. संदीप जैन, डा. अनिल अग्रवाल, डा. हमिता मित्तल सहित एसएमओ डा. आरपी गोयल हैं। फिजिशियन डाक्टर सुरेंद्र नैन और डा. नीलम कक्कड़ को भी ओपीडी में मरीजाें की जांच करनी पड़ती है।ये डाक्टर हुए रिलीवपिछले चार माह में अस्पताल से सर्जन डा. मुनीष बंसल, डा. अमनदीप, डा. अनुमेहा, डा. सुजाता, डा. हरप्रीत, डा. अजय शेर, डा. संजीव कुमार, डा. यशपाल मोमिया, डा. निधि मोमिया, डा. विजय वर्मा में से अधिकतर की या तो ट्रांसफर हो गई। कुछ चिकित्सक अस्पताल छोड़कर ही चले गए।मरीजों को करना पड़ता है इंतजारअस्पताल में उपलब्ध १३ चिकित्सकों को ही आपातकाल, आपरेशन थियेटर, ओपीडी और पोस्टमार्टम का पूरा काम देखना पड़ता है। ऐसे में मरीजों को ओपीडी में चिकित्सकों का घंटों इंतजार करना पड़ता है। मरीज सावित्री देवी, कामना, संजय, विजय, राधिका ने कहा कि उन्हें काफी इंतजार के बाद चिकित्सक को अपनी बीमारी बताए जाने का अवसर मिला। अस्पताल में डाक्टर सीट पर कम ही मिलते हैं।प्रसूति विभाग में हालात खराब २४ घंटे चलने वाले प्रसूति विभाग में ४ में से इस समय डा. सुमन एकमात्र विशेषज्ञ चिकित्सक हैं। उनके साथ एक चिकित्सक हैं, जो मात्र प्रसूति की ट्रेनिंग लेकर आई हैं। इन्हीं डाक्टरों को अस्पताल में दाखिला जच्चा-बच्चा के अलावा प्रतिदिन १५० से २०० गर्भवती महिलाओं की ओपीडी में जांच करनी पड़ती है। सभी पीएचसी, सीएचसी से गर्भवती महिलाओं को यहां रेफर किया जाता है। एक विशेषज्ञ के कारण यहां हालात काफी गंभीर हैं। ऐसे में अंदाजा लगाया जा सकता है २४ गुणा ७ वाली इस प्रसूति सेवा में मरीजों को कितनी परेशानी ओर इंतजार करना पड़ता है। विभाग को भेजी है समस्यासिविल सर्जन डा. सुरेंद्र नैन ने माना कि अस्पताल में डाक्टरों की कमी है। इस बारे में विभाग को सूचित किया गया है। उम्मीद है कि शीघ्र ही अस्पताल में चिकित्सकों की तैनाती होगी। कम चिकित्सकों के बावजूद प्रयास किया जा रहा है कि अस्पताल में आने वाले मरीजों को परेशानी न हो। कैसा लगा | hindi |
Applications are invited from experienced and registered Clinical Psychologists interested in working with children, adolescents and their family/whanau. We are looking for a dynamic clinician to work in a multi disciplinary team across both child and adolescent age groups.
Applicants will be able to provide comprehensive mental health assessments, deliver effective evidence based treatment strategies for young people, and work collaboratively with other team members and services.
Supervision and support will be available and positive learning opportunities given. Mental Health Services in Wairarapa have developed a client pathway based on the Recovery Model and currently exciting service delivery changes are happening.
This position is a permanent part time position working 64 hours per fortnight, Monday to Friday, actual days and times to be arranged.
Applicants for this position must be currently located in NZ and have residency.
We will also accept applications from NZ 2018 new graduates pending registration with the NZ Board of Psychologists.
For further information please contact Jo Van Trigt, Child & Adolescent Mental Health Services Acting Team Leader on (06) 946-9808.
To apply for this role, please visit www.wairarapadhbjobs.co.nz where you can also obtain a copy of the job description for this role. | english |
{% extends "manage/manage_base.html" %}
{% load i18n %}
{% load lfs_tags %}
{% block section %}add-product{% endblock %}
{% block help_link %}user/management/catalog/products.html{% endblock %}
{% block left-slot-wrapper %}{% endblock %}
{% block content %}
<div id="product">
<div id="manage-tabs">
<ul>
<li class="ui-tabs-nav-item"><a href="#data">{% trans 'Add product' %}</a></li>
</ul>
<div id="data">
<h2>{% trans "Data" %}</h2>
<form id="product-data-form"
action="{% url 'lfs_manage_add_product' %}"
method="post">
{% csrf_token %}
{% include "manage/lfs_form.html" %}
<div class="buttons">
<input class="button"
type="submit"
id="product-add-button"
value='{% trans "Add product" %}' />
<input type="button"
class="button"
onclick="window.location='{{ came_from }}'"
value="{% trans 'Cancel' %}" />
</div>
</form>
</div>
</div>
</div>
<script>
$(function() {
$("#id_name").on("keyup", function() {
var slug = $("#id_name").val()
slug = URLify(slug, 200)
$("#id_slug").val(slug);
});
});
</script>
{% endblock %}
| code |
\begin{document}
\title{On representations of dialgebras and conformal algebras}
\author{Pavel Kolesnikov}
\address{Sobolev Institute of Mathematics \\
Novosibirsk, Russia}
\email{pavelsk@math.nsc.ru}
\begin{abstract}
In this note, we observe a relation between dialgebras
(in particular, Leibniz algebras) and
conformal algebras. The purpose is to show how
the methods of conformal algebras help solving problems on
dialgebras, and, conversely, how the ideas of dialgebras work
for conformal algebras.
\end{abstract}
\keywords{Leibniz algebra; Dialgebra; Vertex operator algebra; Conformal algebra.}
\maketitle
\section{Conformal Algebras}
The notion of a conformal algebra was introduced
in \cite{Kac1998} (in \cite{Primc1999}, a similar notion
appeared under the name of a vertex Lie algebra).
This notion is an important tool for studying vertex operator
algebras. The latter came into algebra from mathematical physics
(namely, from the 2-dimensional conformal field theory, what
explains the name ``conformal algebra"), that was initiated by
\cite{BPZ1984}. The algebraic essence of vertex operator structures
was extracted in \cite{Bor1986} and later developed in a series of
works, e.g., \cite{FLM1988, DongLep1993, Li1996}.
The relations between vertex and conformal algebras are very much
similar to the relations between ordinary associative and Lie algebras.
In conformal field theory, the
operator product expansion (OPE) describes the
commutator of two fields.
Let $V$ be a (complex) space of states, and let $Y:V\to \mathrm{End}\,V[[z,z^{-1}]]$,
$Y:b\mapsto Y(b,z)$,
be a state-field correspondence of a vertex algebra.
Then the
commutator of two fields can be expressed as a finite distribution
\[
[Y(a,w),Y(b,z)] = \sum\limits_{n\ge 0} \dfrac{1}{n!} Y(c_n, z)
\dfrac{\partial^n\delta(w-z)}{\partial z^n},\quad a,b\in V,
\]
where $c_n\in V$,
$\delta(w-z)=\sum\limits_{m\in \mathbb Z} w^m z^{-m-1}$
is the formal delta-function.
The formal Fourier transformation
\begin{equation}\label{eq: ResLambdaProd}
[Y(a,z)_\lambda Y(b,z)] =
\mathrm{Res}_{w=0} \exp\{\lambda (w-z)\}[Y(a,w),Y(b,z)]
\end{equation}
is called the $\lambda $-bracket on the space
of fields $\{Y(a,z)\mid a\in V\}$.
Here $\lambda $ is a new formal variable, and
$\mathrm{Res}_{w=0}F(w,z) $ means the residue at
$w=0$, i.e., the formal series in $z$ that is
a coefficient of $F(w,z)$ at~$w^{-1}$.
The algebraic properties of the $\lambda $-bracket \eqref{eq: ResLambdaProd}
lead to the formal definition of a conformal algebra
over a field $\Bbbk $ of characteristic~0.
\begin{definition}[{\cite{Kac1998}}] \label{defn:Conformal Algebra}
A conformal algebra is a left (unital) module $C$ over the
polynomial algebra $H=\Bbbk [T]$ endowed with a binary
$\Bbbk$-linear operation
\begin{equation}\label{eq:LambdaProduct}
(\cdot{}_\lambda \cdot): C\otimes C \to C[\lambda ] ,
\end{equation}
such that
$(Ta_\lambda b) = -\lambda (a_\lambda b)$,
$(a_\lambda D b) = (T+\lambda )(a_\lambda b)$.
\end{definition}
In terms of fields, $T$ is just the ordinary derivation with respect to~$z$.
Every conformal algebra can be represented by formal distributions
over an ordinary algebra. Let $C$ be an object described by
Definition \ref{defn:Conformal Algebra}.
Consider the space of Laurent polynomials $\Bbbk[t,t^{-1}]$ as a
right $H$-module with respect to the following action:
$f(t)T = -f'(t)$.
Then
\[
\mathcal A(C) = \Bbbk[t,t^{-1}]\otimes _H C
\]
carries the natural algebra structure:
\[
(f\otimes _H a)\cdot (g\otimes_H b) = (g\otimes_H 1)(f\otimes _H (a_{-T} b)),
\quad a,b\in C,\ f,g\in \Bbbk[t,t^{-1}].
\]
The space of formal distributions $\mathcal A(C)[[z,z^{-1}]]$
that consists of all series
\[
Y(a,z)=\sum\limits_{n\in \mathbb Z} (t^n\otimes_H a)z^{-n-1},
\quad
a\in C,
\]
can be endowed with the action of $T=d/dz$ and with a $\lambda $-bracket
$(\cdot {}_\lambda \cdot)$
similar to \eqref{eq: ResLambdaProd}, where the commutator
is replaced with the ordinary product of distributions.
Then
\[
(Y(a,z)_\lambda Y(b,z)) =Y((a_\lambda b),z), \quad a,b\in C,
\]
i.e., $C$ is isomorphic to a formal distribution conformal algebra
over $\mathcal A(C)$.
The algebra $\mathcal A(C)$ is called the coefficient algebra \cite{Roitman1999}
of $C$, or annihilation algebra \cite{Kac1998}.
\begin{definition}[{\cite{Roitman1999}}]\label{defn:VarConformal}
Let $\mathcal V$ be a variety of algebras (associative, alternative, Lie, etc.).
Then a conformal algebra $C$ is said to be $\mathcal V$-conformal algebra
if $\mathcal A(C)$ belongs to~$\mathcal V$.
\end{definition}
Associative and Lie conformal algebras, their representations, and cohomologies
have been studied in a series of papers, e.g.,
\cite{BKV1999, DK1998, CK1997, Roitman2000,
BKL2003, Retakh2001, KacRetakh2008}.
In particular, associative conformal algebras naturally appear
in the study of representations of Lie conformal algebras.
\begin{example}\label{exm:CurrentAlgebra}
Consider one of the simplest (though important) examples of conformal algebras.
Suppose $A$ is an ordinary algebra
(not necessarily associative or Lie). Then the free $H$-module
\[
\mathrm{Cur}\,A = H\otimes A
\]
generated by the space $A$ endowed
with the $\lambda $-bracket
$(f(T)\otimes a)_\lambda (g(T)\otimes b) =
f(-\lambda )g(T+\lambda )\otimes ab$,
is called the current conformal algebra.
\end{example}
If $A$ belongs to a variety $\mathcal V$ defined by a family of
polylinear identities then $\mathrm{Cur}\, A$ is a $\mathcal V$-conformal
algebra.
Certainly, current conformal algebras and their subalgebras do not exhaust
the entire class of conformal algebras. For example, $W=\Bbbk[T,x]$
with respect to the operation
\[
(f(T,x)_\lambda g(T,x)) = f(-\lambda , T)g(T+\lambda , x+\lambda)
\]
is an associative conformal algebra (called Weyl conformal algebra \cite{Roitman1999}),
and $\mathrm{Vir}=\Bbbk[T]$ with respect to
\[
( f(T)_\lambda g(T) ) = f(-\lambda )g(T+\lambda )(T+2\lambda )
\]
is a Lie conformal algebra (called Virasoro conformal algebra \cite{Kac1998}).
Conformal algebra is said to be finite if it is a finitely generated $H$-module.
\section{Dialgebras}
The following notion appears naturally from a
certain noncommutative analogue of Lie homology theory.
\begin{definition}[{\cite{Loday1993}}]\label{defn:LeibnizAlgebra}
A (left) Leibniz algebra is a linear space $L$ with a bilinear operation
$[\cdot ,\cdot ]$ such that
\[
[x,[y,z]]= [[x,y],z] + [y,[x,z]], \quad x,y,z\in L.
\]
\end{definition}
The defining identity means that the operator of
left multiplication $[x,\cdot]$ is a derivation of $L$.
Leibniz algebras are the most popular noncommutative generalizations
of Lie algebras. The following
structures play the role of associative enveloping algebras for
Leibniz algebras.
\begin{definition}[{\cite{Loday1995}}]\label{defn:AssocDialgebras}
An associative dialgebra (or {\em diassociative algebra}) is a linear space $D$ endowed
with two bilinear operations $(\cdot\dashv\cdot)$, $(\cdot\vdash\cdot)$
such that
\begin{gather}
x \dashv (y\vdash z) = x \dashv (y \dashv z), \quad
(x \dashv y)\vdash z = (x \vdash y) \vdash z,
\label{eq:0-ident}\\
x \vdash (y\vdash z) = (x \vdash y) \vdash z, \label{eq:DiAss1}\\
x \dashv (y\dashv z) = (x \dashv y) \dashv z,\label{eq:DiAss2}\\
x \vdash (y\dashv z) = (x \vdash y) \dashv z, \label{eq:DiAss3}
\end{gather}
for all $x,y,z\in D$.
\end{definition}
In particular, the operation
$[a,b]=a\vdash b - b\dashv a$, $a,b\in D$,
turns a diassociative algebra $D$ into a Leibniz algebra
denoted by $D^{(-)}$.
A systematical study of diassociative algebras was performed in
\cite{Loday2001}.
Also, in \cite{LiuDong2005} and \cite{Chap2001}
the notions of alternative and commutative dialgebras were introduced.
These definitions also appear in the general categorical approach
using the language of operads \cite{Kol2008a}.
Shortly speaking, an operad $A$
is a collection of spaces $A(n)$, $n\ge 1$, such that a
composition rule $A(n)\otimes A(m_1)\otimes \dots \otimes A(m_n)
\to A(m_1+\dots + m_n)$
and an action of a symmetric group are defined in such a way
that some natural axioms hold (associativity of a composition,
existence of a unit in $A(1)$, and equivariance of the composition
with respect to the symmetric group action).
A linear space $A$ over a field $\Bbbk $ may be considered
as an operad (see, e.g., \cite{Leinster2004} as a general reference),
where $A(n)=\mathrm{Hom}\,(A^{\otimes n}, A)$.
In the free operad denoted by $\mathrm{Alg}$,
the spaces $\mathrm{Alg}(n)$ are spanned by (planar)
binary trees with $n$ leaves.
An algebra structure on a linear space
$A$ is just a functor of operads $\mathrm{Alg} \to A$.
If $\mathcal V$ is a variety of algebras defined by
polylinear identities then there exists a free $\mathcal V$-operad
$\mathcal V\hbox{-}\mathrm{Alg}$
built on polylinear polynomials of the free $\mathcal V$-algebra.
There exists a canonical functor $\mathrm{Alg}\to \mathcal V\hbox{-}\mathrm{Alg}$,
and it is clear that an algebra $A$ belongs to $\mathcal V$
if and only if there exists a functor
$\mathcal V\hbox{-}\mathrm{Alg} \to A$ such that the following diagram is commutative:
\[
\begin{array}{c@{} c@{} c@{} c@{} c}
\mathrm{Alg} & &\longrightarrow& &A\\
& \searrow && \nearrow \\
& &\mathcal V\hbox{-}\mathrm{Alg}
\end{array}
\]
A similar definition works for dialgebras. An operad
$\mathrm{Dialg}$ whose spaces are spanned by planar
binary trees with 2-colored vertices (colors 1~and~2 stand for $\vdash$
and $\dashv $, respectively) has an image equivalent to
the Hadamard product $\mathrm{Alg}\otimes \mathcal E$,
where $\mathcal E $ is the free $\mathcal V_c$-operad
corresponding to the variety $\mathcal V_c$ of associative and commutative
dialgebras (Perm-algebras), $\dim \mathcal E(n)=n$ (see \cite{Chap2001, Kol2008a} for details).
Suppose
$\mathcal V$ is a variety of algebras defined by
polylinear identities.
For a linear space $D$, a functor $\mathrm{Dialg} \to D$
defines two bilinear operations $\vdash$ and~$\dashv$ on $D$. Conversely, any system
$(D,\vdash, \dashv)$ may be considered as a functor $\mathrm{Dialg} \to D$.
\begin{definition}[{\cite{Kol2008a}}]\label{defn:Var-Dialg}
A linear space $D$ with two bilinear operations $\vdash$ and~$\dashv$
is said to be di-$\mathcal V$-algebra if there exists a functor
$\mathcal{V}\hbox{-}\mathrm{Alg}\otimes \mathcal E\to D$
such that the following diagram
is commutative:
\[
\begin{CD}
\mathrm{Dialg} @>>> D \\
@VVV @VVV \\
\mathrm{Alg}\otimes \mathcal E @>>> \mathcal V\hbox{-}\mathrm{Alg}\otimes \mathcal E
\end{CD}
\]
\end{definition}
We will mainly use the term ``di-$\mathcal V$-algebra'', but this is the same as
``$\mathcal V$-dialgebra''.
The last definition is easy to translate into the language of
identities. First, identify
$\mathrm{Alg}(n)$
with the space of polylinear non-associative polynomials in
$x_1,\dots, x_n$; for $\mathrm{Dialg}$ we have a similar interpretation.
Next, consider the following linear maps
$\Psi_k: \mathrm{Alg}(n)\to \mathrm{Dialg}(n)$, $k=1,\dots, n$:
\[
\Psi_k: (x_{j_1}\dots x_k \dots x_{j_n}) \mapsto (x_{j_1}\vdash \dots \vdash
x_k
\dashv \dots \dashv x_{j_n}),
\]
assuming the bracketing $(\dots )$ on monomials is preserved.
Then we have
\begin{theorem}[{\cite{Kol2008a}}]\label{thm:Dias-Identity}
Assume $\{f_i\mid i\in I\}$ is the family of polylinear defining
identities of a variety $\mathcal V$.
Then $D$ is a di-$\mathcal V$-algebra if and
only if $D$ satisfies the identities $\Psi_k(f_i)=0$
for all $i\in I$, $k=1, \dots, \deg f_i$.
\end{theorem}
If $\mathcal V$ is the variety of Lie algebras then
$f = x_1x_2+x_2x_1$ is one of its defining identities.
Since $\Psi_1(f)=x_1\dashv x_2 + x_2\vdash x_1$,
we can describe Lie dialgebras in terms of single operation, say,
$[a,b]=a\vdash b$. Then the class of Lie dialgebras coincides
with the class of Leibniz algebras.
Note that all di-$\mathcal V$-algebras satisfy the relations
\eqref{eq:0-ident}, called 0-identities \cite{Kol2008a}.
The following approach to the definition of varieties
of dialgebras was proposed in~\cite{Pozh2009}.
Let $D$ be a dialgebra that satisfies 0-identities. Then
the linear span $D_0$ of all elements
$a\vdash b - a\dashv b$, $a,b\in D$, is an ideal of~$D$.
The quotient $\bar D=D/D_0$ is an ordinary algebra with a
single operation. Moreover, the following actions are well-defined:
\[
\begin{aligned}
& \bar D\otimes D \to D, \\
& (a+D_0)\otimes b \mapsto a\vdash b,
\end{aligned}
\qquad \qquad
\begin{aligned}
& D\otimes \bar D \to D, \\
& a\otimes (b+D_0) \mapsto a\dashv b.
\end{aligned}
\]
Denote by $\hat D$ the split null extension $\bar D\oplus D$,
assuming $D^2=0$.
\begin{theorem}[{\cite{Pozh2009}}]\label{thm:EilengerghDefn}
Suppose $\mathcal V$ is a variety of algebras with
polylinear defining identities. Then $D$ is a
di-$\mathcal V$-algebra if and only if $D$ satisfies
the 0-identities and $\hat D$ is an algebra from~$\mathcal V$.
\end{theorem}
A curious relation between conformal algebras and dialgebras
was noted in~\cite{Kol2008a}. It turns out that
if $C$ is a $\mathcal V$-conformal algebra in the sense
of Definition \ref{defn:VarConformal} then
the same linear space endowed with just two operations
\[
a\vdash b = (a_\lambda b)|_{\lambda =0}, \quad
a\dashv b = (a_\lambda b)|_{\lambda =-T}, \quad a,b\in C,
\]
is a di-$\mathcal V$-algebra denoted by $C^{(0)}$.
Conversely, every di-$\mathcal V$-algebra can be embedded into
an appropriate $\mathcal V$-conformal algebra.
The last statement easily follows from Theorem \ref{thm:EilengerghDefn}
and
\begin{theorem}[{c.f. \cite{KolGub2009}}]\label{thm:CurrEmbedding}
Let $D$ be a dialgebra satisfying the 0-identities.
Then the map $D\to H\otimes \hat D$, $a\mapsto 1\otimes (a+D_0) + T\otimes a$,
$a\in D$, is an injective homomorphism of
dialgebras $D\to (\mathrm{Cur}\,\hat D)^{(0)}$.
Therefore, $D$ is a di-$\mathcal V$-algebra if and only if there exists
a $\mathcal V$-algebra $A$ such that $D\subseteq (\mathrm{Cur}\,A)^{(0)}$.
\end{theorem}
Thus, there are three equivalent definitions of what is a dialgebra of
a given variety provided by Theorems~\ref{thm:Dias-Identity},
\ref{thm:EilengerghDefn}, and~\ref{thm:CurrEmbedding}.
\section{Some Classical Theorems for Leibniz Algebras}
Since Leibniz algebras are just Lie dialgebras in the sense of
Definition~\ref{defn:Var-Dialg}, we may use
Theorem~\ref{thm:CurrEmbedding} to get natural generalizations of
some classical statements on Lie algebras to the class of Leibniz algebras.
These are: the Engel Theorem, the Poincar\'e---Birkhoff---Witt (PBW) Theorem,
and the Ado Theorem.
We will need the following statement (c.f.~Theorem~3 in~\cite{Kol2008b}).
\begin{theorem}\label{thm:ConfRepresentation}
Let $L$ be a Leibniz algebra, and let $V$ be a module over the
Lie algebra $\bar L$. Then there exists an injective homomorphism
$\rho: L\to (\mathrm{Cur}\,\mathrm{gl}(V\oplus (L\otimes V)))^{(0)}$
of Leibniz algebras.
\end{theorem}
\begin{proof}
For every $x\in L$, denote $\bar x=x+L_0\in \bar L$ and define
$\rho(x)\in H\otimes \mathrm{gl}(V\oplus (L\otimes V))$ as follows:
\[
\rho(x) = 1\otimes \rho_0(x) + T\otimes \rho_1(x),
\quad \rho_i(x)\in \mathrm{gl}(V\oplus (L\otimes V)),
\]
where
\[
\begin{aligned}
\rho_0(x) &: v\mapsto \bar x v, \\
\rho_0(x) &: a\otimes v \mapsto a\otimes \bar x v + [x,a]\otimes v, \\
\rho_1(x) &: v\mapsto x\otimes v, \\
\rho_1(x) &: a\otimes v \mapsto 0
\end{aligned}
\]
for all $a\in L$, $v\in V$.
It is clear that $\rho $ is injective ($\rho_1(x)\ne 0$ for $x\ne 0$).
Let us check that $\rho $ is a homomorphism of Leibniz algebras.
First,
$(\rho(x)_\lambda \rho(y))
= [1\otimes \rho_0(x)-1\otimes \lambda \rho_1(x), 1\otimes \rho_0(y)+(T+\lambda)\rho_1(y)]$.
for all $x,y\in L$.
Hence,
$[\rho(x), \rho(y)]=1\otimes [\rho_0(x), \rho_0(y)] +
T\otimes [\rho_0(x),\rho_1(y)]$.
Next, it is straightforward to compute
\[
\begin{aligned}{}
[\rho_0(x),\rho_0(y)] &:v+(a\otimes w)\mapsto
[\bar x,\bar y]v + a\otimes [\bar x,\bar y]w + [[x,y],a]\otimes w, \\
[\rho_0(x),\rho_1(y)] &:v+(a\otimes w)\mapsto [x,y]\otimes v
\end{aligned}
\]
for all $v,w\in V$, $a\in L$.
Therefore,
$[\rho_0(x),\rho_0(y)]=\rho_0([x,y])$,
$[\rho_0(x),\rho_1(y)]=\rho_1([x,y])$, i.e.,
$[\rho(x), \rho(y)]=\rho([x,y])$.
\end{proof}
The following statement immediately follows from
Theorem~\ref{thm:ConfRepresentation} applied to $V=L$.
\begin{theorem}[{\cite{AyOmir1998, Pats2007, Barn2010}}]\label{thm:Engel}
Let $L$ be a finite-dimensional Leibniz algebra
such that all operators $[x,\cdot]\in \mathrm{End}\, L$ are nilpotent.
Then $L$ itself is a nilpotent Leibniz algebra.
\end{theorem}
Recall that for a Lie algebra $L$ the classical PBW Theorem states
that the universal enveloping associative algebra $U(L)$ is isomorphic
(as a linear space) to the symmetric algebra $S(L)$.
For Leibniz algebras, the role of associative envelopes belongs to
diassociative algebras.
\begin{theorem}[{\cite{Loday2001, AymonGr2003}}]\label{thm:PBWLeibniz}
The universal enveloping diassociative algebra $Ud(L)$
of a Leibniz algebra $L$ is isomorphic (as a linear space) to
$U(\bar L)\otimes L$.
\end{theorem}
As in the case of Lie algebras, the main technical difficulty in the
proof of the PBW Theorem for Leibniz algebras is to show that ``normal"
monomials are linearly independent. In \cite{BokutChen2009}, another
proof of this independence was obtained by making use of Gr\"obner---Shirshov
bases theory for diassociative algebras. However, one may just apply
Theorem~\ref{thm:ConfRepresentation} to $V=U(\bar L)$,
see \cite{Kol2008b} for details.
Another interesting question is similar to the Ado Theorem: Whether
a finite-dimensional Leibniz algebra can be embedded into a
finite-dimensional diassociative algebra?
It turns out, the answer is positive. Indeed, it is enough to apply
Theorem~\ref{thm:ConfRepresentation} to $V=\Bbbk $, a trivial 1-dimensional
module over $\bar L$. In particular, we may conclude that an $n$-dimensional
Leibniz algebra can be embedded into a diassociative algebra $D$ such
that $\dim D\le 2(n+1)^2$.
\section{Di-Jordan algebras}
A diassociative algebra $D$ turns into a Leibniz algebra $D^{(-)}$
if we define the bracket $[x,y]=x\vdash y - y\dashv x$.
This is natural to expect that if we define new operation
\[
x\circ y = x\vdash y + y\dashv x, \quad x,y\in D,
\]
then the algebra $D^{(+)}=(D,\circ ) $
obtained would be a noncommutative analogue
of a Jordan algebra. Roughly speaking, it relates to Jordan algebras in the
same way as Leibniz algebras relate to Lie algebras.
This is indeed a di-Jordan algebra; the commutativity identity turns
into
\[
\Psi_1(x_1x_2-x_2x_1)=x_1\dashv x_2 - x_2\vdash x_1,
\]
so we may
describe this algebra with only one operation.
Objects of this type appeared also in~\cite{VF2009, Brem2009}.
\begin{definition}
A di-Jordan algebra is a linear space with a bilinear product satisfying the
following identities:
\begin{equation} \label{eq:JorDiasAlg}
\begin{gathered}[]
[x_1, x_2]x_3= 0, \\
(x_1^2,x_2,x_3)=2(x_1,x_2,x_1x_3),
\quad
x_1(x_1^2 x_2)=x_1^2(x_1 x_2).
\end{gathered}
\end{equation}
\end{definition}
Here $[a,b]$ and $(a,b,c)$ stand for the commutator $ab-ba$ and associator $(ab)c-a(bc)$,
respectively. The first identity in \eqref{eq:JorDiasAlg} comes from the 0-identities,
the second and third appear from the Jordan identity.
In \cite{BremPeresi2010} these algebras were called
semi-special quasi-Jordan algebras.
Recall that a Jordan algebra $J$ is said to be special if there exists
an associative algebra $A$ such that $J\subseteq A^{(+)}$. The class of
all homomorphic images of all special Jordan algebras is a variety denoted
by $\mathrm{SJ}$.
This is well-known that $\mathrm{SJ}$ does not coincide with the variety
of all Jordan algebras.
Those defining identities of $\mathrm{SJ}$ that do
not hold in all Jordan algebras
are called special identities (or s-identities, for short).
I was shown in \cite{Glenie1970} that the minimal degree of an
s-identity is equal to~8. However, the description of all s-identities
is still an open problem.
For di-Jordan algebras, the same theory makes sense.
\begin{definition}[{\cite{BremPeresi2010}}]
A di-Jordan algebra $J$ is said to be special if
there exists a diassociative algebra $D$ such that
$J\subseteq D^{(+)}$.
\end{definition}
It is clear that the class of all homomorphic images of all
special di-Jordan algebras is a variety. Let us denote this variety
by $\mathrm{DiSJ}$. The notion of an s-identity for di-Jordan algebras
is a natural generalization of s-identities for Jordan algebras.
The following statement was proved in \cite{BremPeresi2010}
by making use of computer algebra methods.
\begin{theorem}[{\cite{BremPeresi2010}}]\label{thm:Di-Sidentities}
{\em 1.} For di-Jordan algebras, there are no s-identities of degree $\le 7$;\\
{\em 2.} There exists an identity of degree~8 that holds on all special di-Jordan
algebras and on all Jordan algebras, but does not hold on all
di-Jordan algebras.
\end{theorem}
On the other hand, the variety $\mathrm{SJ}$ leads to the notion of
a di-$\mathrm{SJ}$-algebra by Definition~\ref{defn:Var-Dialg}. It turns
out that these two different approaches lead to the same class of
dialgebras.
\begin{theorem}[{\cite{Voron2010}}]\label{thm:DiSJ=SJDi}
The variety of di-$\mathrm{SJ}$-algebras coincides with $\mathrm{DiSJ}$.
\end{theorem}
This fact allows to deduce a correspondence between s-identities for
Jordan algebras and dialgebras.
\begin{theorem}[{\cite{Voron2010}}]\label{thm:SId-Correspond}
Let $f(x_1,\dots, x_n)$ be a polylinear s-identity for Jordan algebras. Then
$\Psi_k f$, $k=1,\dots, n$,
is an s-identity for di-Jordan algebras.
Conversely, if $g(x_1,\dots, x_n)$ is an
s-identity for di-Jordan algebras then
\[
g(x_1,\dots, x_n)=\sum\limits_{k=1}^n g_k, \quad g_k=\Psi_k(f_k)
\]
for some nonassociative polynomials $f_k(x_1, \dots, x_n)$,
and at least one of $f_k$ is an s-identity for Jordan algebras.
\end{theorem}
Note that Theorem~\ref{thm:SId-Correspond} works for polylinear identities
only, so it says nothing about the identity
from Theorem~\ref{thm:Di-Sidentities}(2).
A series of classical results for special Jordan algebras can be transferred
to dialgebras. In particular, the Shirshov---Cohn Theorem states that
every 2-generated Jordan algebra is special. It turns out that the free
2-generated di-Jordan algebra is special, but its homomorphic image
may not be special \cite{Voron2010}. However, Theorem~\ref{thm:CurrEmbedding}
implies that every 1-generated di-Jordan algebra is special.
Another problem on di-Jordan algebras concerns their relation to Leibniz algebras.
The classical Tits---Kantor---Koecher construction allows to build a
Lie algebra $T(J)$ for a given Jordan algebra $J$ in such a way that structure
of $J$ is closely related with the structure of $T(J)$.
This is natural to expect \cite{VF2009} that a similar construction for a di-Jordan algebra
should lead to Lie dialgebra, i.e., Leibniz algebra.
Conformal algebras allow to solve this problem.
Let $J$ be a di-Jordan algebra, and let $\hat J$ stands
for the split null extension $\bar J\oplus J$
(see Theorem~\ref{thm:EilengerghDefn}).
This is a Jordan algebra, and it follows from Theorem~\ref{thm:CurrEmbedding}
that $J\subseteq (\mathrm{Cur}\,\hat J)^{(0)}$.
Denote by
\[
T(\hat J) = {\hat J}^+ \oplus S(\hat J) \oplus {\hat J}^-
\]
the Tits---Kantor---Koecher construction \cite{Kantor1964,Koecher1967,Tits1962}
for~$\hat J$.
Here ${\hat J}^{\pm}$ are linear spaces isomorphic to $\hat J$, and
$S(\hat J)\subseteq \mathrm{End}\, \hat J\oplus \mathrm{Der}\, \hat J$
is spanned by
\[
U_{a,b} = L_{ab} + [L_a,L_b], \quad a,b\in \hat J,
\]
where $L_x$ denotes the operator of left multiplication:
$L_x(y)=xy$.
The images of $a\in J$ in the isomorphic copies $J^{\pm}$ are denoted
by~$a^\pm$.
This is a Lie algebra, $J^+$ and $J^-$ are its abelian subalgebras, and
$[a^-, b^+] = L_{ab} + [L_a, L_b]$ for $a,b\in J$. Therefore,
$\mathcal L(J) = (\mathrm{Cur}\,T(\hat J))^{(0)}$ is a
Leibniz algebra.
Then the elements $1\otimes (a+J_0)^\pm + T\otimes a^\pm \in \mathcal L(J)$,
$a\in J$,
generate a Leibniz algebra $T(J)$
\begin{theorem}[{\cite{KolGub2009}}]
Let $J$ be a di-Jordan algebra.
Then $T(J)$ is a solvable Leibniz algebra if and only if
$J$ is a Penico solvable \cite{JacJordan}; $T(J)$ is nilpotent if
and only if so is~$J$.
\end{theorem}
\section{On Embeddings of Conformal Algebras}
One of the basic facts about associative algebras states that
every finite-dimen\-sional associative algebra $A$ can be presented
by matrices. Indeed, even if $A$ does not contain a unit element,
we may consider $A^\#=A\oplus \Bbbk 1$, and then there is a
faithful representation $L:A\to \mathrm{End}\,A^\#$,
$L(a): x\to ax$.
For a conformal algebra $C$ of rank $n$ over $H$, the role of $\mathrm{End}\, A$ belongs
to $\mathrm{Cend}\,C$, which is isomorphic to the conformal algebra
of $n\times n$ matrices over the Weyl conformal algebra.
The following properties define an analogue of the unit element for
conformal algebras.
\begin{definition}[{\cite{Retakh2001}}]\label{defn:Unit}
Suppose $C$ is a conformal algebra. An element $e\in C$
is said to be a (conformal) unit in $C$ if
$(e_\lambda x)|_{\lambda=0} = x$ for all $x\in C$ and
$e_\lambda e = e$.
\end{definition}
Associative conformal algebra with a unit has a very natural structure.
\begin{proposition}[{\cite{Retakh2001}}]\label{prop:DiffAlgebra}
Let $C$ be a semisimple associative conformal algebra with a unit.
Then there exists an associative algebra $A$ with a locally
nilpotent derivation $\partial $ such that $C\simeq H\otimes A$
with respect to the operation
\[
(f(T)\otimes a)_\lambda (g(T)\otimes b) = f(-\lambda )g(T+\lambda )\otimes
a\exp\{\lambda \partial\}b,\quad a,b\in A,\ f,g\in H.
\]
\end{proposition}
\begin{remark}
In particular, if $\partial =0$ then such $C$ is just the current algebra
$\mathrm{Cur}\,A$; if $A=\Bbbk[x]$ and $\partial = d/dx$ then $C$ is the
Weyl conformal algebra.
\end{remark}
This is the reason why the following problem \cite{Retakh2004} makes sense:
Is it possible to join a conformal unit to an associative conformal algebra.
Moreover, a finite associative conformal algebra can be embedded into
matrices over the conformal Weyl algebra if and only if one can join a
unit to this conformal algebra.
The following statement answers positively to this question.
\begin{theorem}[{\cite{Kol2010}}]\label{thm:UnitEmbedding}
If $C$ is a finite associative conformal algebra which is a
torsion-free $H$-module then there exists an associative
conformal algebra $C_e$ with a unit such that $C\subseteq C_e$.
\end{theorem}
The last Theorem does not hold for all conformal algebras.
For example, consider the free $H$-module $C$ generated by the space
$W=\Bbbk[x]\oplus \Bbbk w$ with the following operation on generators:
\[
W_\lambda w = 0, \quad
f(x)_\lambda g(x)=f(x-T-\lambda)g(x ), \quad
w_\lambda f(x) = f(T)w,
\]
for $f,g\in \Bbbk[x]$. This is an associative conformal algebra.
Assume there exists a unital conformal algebra $C_e$
with unit $e$
such that $C\subseteq C_e$. Then associativity implies
\[
((e_\lambda w)_0 x^n) = (e_\lambda (w_{-\lambda} x^n)) = e_\lambda T^nw =
(T+\lambda )^n (e_\lambda w), \ n\ge 1.
\]
This is impossible since $(e_\lambda w)$ is a polynomial in $\lambda $,
and its degree does not depend on the choice of $n$, except for
$(e_\lambda w)=0$. But $(e_{0 } w)=w$ by the definition of a conformal
unit. The contradiction obtained shows that $C_e$ does not exist.
Another problem on embeddings of conformal algebras concerns the following
observation.
If $C$ is an associative conformal algebra
with operations $T:C\to C$ and $(\cdot{}_\lambda \cdot):C\otimes C\to C[\lambda ]$
then the same module over $H=\Bbbk[T]$ with respect to the new operation
\[
[x_\lambda y ] = (x_\lambda y) - (y_{\mu }x)|_{\mu=-T-\lambda}
\]
is a Lie conformal algebra \cite{Kac1998}. It is natural
to denote this conformal algebra by~$C^{(-)}$.
In contrast to the case of ordinary algebras, there exist Lie conformal algebras
that can not be embedded into associative conformal algebras \cite{Roitman2000}.
However, it is unknown whether the following statement is true.
\begin{conjecture}\label{conj:Ado}
Suppose $L$ is a finite Lie conformal algebra which is a torsion-free
$H$-module.
Then $L$ can be embedded into an associative conformal algebra with unit.
\end{conjecture}
It was shown in \cite{DK1998}
that every such $L$ has a maximal solvable ideal $R$, so $L/R$ is semisimple.
The conjecture obviously holds for semisimple conformal algebras.
In \cite{Roitman2006}, it was shown that a nilpotent Lie conformal algebra
can be embedded into a nilpotent associative conformal algebra with the same index
of nilpotency.
This proves Conjecture~\ref{conj:Ado} for nilpotent algebras, but it
actually holds in much more general class of Lie conformal algebras that
includes finite torsion-free solvable algebras.
The idea comes from the construction of a
conformal representation for a Leibniz algebra in
Theorem~\ref{thm:ConfRepresentation}.
Let us first consider a Lie conformal algebra of the type
$L=\mathrm{Cur}\,\mathfrak g$, where $\mathfrak g$ is a Lie algebra,
$\dim \mathfrak g<\infty $.
This is straightforward to check that the embedding built in the proof of
Theorem~\ref{thm:ConfRepresentation}
is in fact a homomorphism of conformal algebras.
This proves Conjecture~\ref{conj:Ado}
without a reference to the classical Ado Theorem.
In the more general case, the Lie Theorem for conformal algebras
proved in \cite{DK1998} allows to deduce the following fact.
\begin{theorem}[{\cite{Kol2010}}]
Suppose $L$ is a Lie conformal algebra which is a semi-direct product
of a current conformal algebra $\mathrm{Cur}\,\mathfrak g$
($\dim\mathfrak g<\infty$)
and a finite torsion-free solvable Lie conformal algebra $R$.
Then there exists a finite-dimensional associative algebra $A$
such that $L\subseteq (\mathrm{Cur}\,A)^{(-)}$.
\end{theorem}
\section*{Acknowledgments}
This work was partially supported by
RFBR 09-01-00157, SSc 3669.2010.1,
SB RAS Integration project N 97,
Federal Target Grants 02.740.11.0429, 02.740.11.5191, 14.740.11.0346,
and by the ADTP Grant 2.1.1.10726.
\end{document} | math |
# Makefile for staging directory
# fix for build system bug...
obj-$(CONFIG_STAGING) += staging.o
obj-y += serial/
obj-y += media/
obj-$(CONFIG_ET131X) += et131x/
obj-$(CONFIG_SLICOSS) += slicoss/
obj-$(CONFIG_USBIP_CORE) += usbip/
obj-$(CONFIG_W35UND) += winbond/
obj-$(CONFIG_PRISM2_USB) += wlan-ng/
obj-$(CONFIG_ECHO) += echo/
obj-$(CONFIG_COMEDI) += comedi/
obj-$(CONFIG_FB_OLPC_DCON) += olpc_dcon/
obj-$(CONFIG_ASUS_OLED) += asus_oled/
obj-$(CONFIG_PANEL) += panel/
obj-$(CONFIG_R8187SE) += rtl8187se/
obj-$(CONFIG_RTL8192U) += rtl8192u/
obj-$(CONFIG_RTL8192E) += rtl8192e/
obj-$(CONFIG_R8712U) += rtl8712/
obj-$(CONFIG_RTS_PSTOR) += rts_pstor/
obj-$(CONFIG_RTS5139) += rts5139/
obj-$(CONFIG_TRANZPORT) += frontier/
obj-$(CONFIG_IDE_PHISON) += phison/
obj-$(CONFIG_LINE6_USB) += line6/
obj-$(CONFIG_USB_SERIAL_QUATECH2) += serqt_usb2/
obj-$(CONFIG_USB_SERIAL_QUATECH_USB2) += quatech_usb2/
obj-$(CONFIG_OCTEON_ETHERNET) += octeon/
obj-$(CONFIG_VT6655) += vt6655/
obj-$(CONFIG_VT6656) += vt6656/
obj-$(CONFIG_VME_BUS) += vme/
obj-$(CONFIG_DX_SEP) += sep/
#obj-$(CONFIG_IIO) += iio/
obj-$(CONFIG_ZCACHE) += zcache/
obj-$(CONFIG_WLAGS49_H2) += wlags49_h2/
obj-$(CONFIG_WLAGS49_H25) += wlags49_h25/
obj-$(CONFIG_FB_SM7XX) += sm7xx/
obj-$(CONFIG_CRYSTALHD) += crystalhd/
obj-$(CONFIG_CXT1E1) += cxt1e1/
obj-$(CONFIG_FB_XGI) += xgifb/
obj-$(CONFIG_TIDSPBRIDGE) += tidspbridge/
obj-$(CONFIG_ACPI_QUICKSTART) += quickstart/
obj-$(CONFIG_SBE_2T3E3) += sbe-2t3e3/
obj-$(CONFIG_USB_ENESTORAGE) += keucr/
obj-$(CONFIG_BCM_WIMAX) += bcm/
obj-$(CONFIG_FT1000) += ft1000/
obj-$(CONFIG_SPEAKUP) += speakup/
obj-$(CONFIG_TOUCHSCREEN_CLEARPAD_TM1217) += cptm1217/
obj-$(CONFIG_TOUCHSCREEN_SYNAPTICS_I2C_RMI4) += ste_rmi4/
obj-$(CONFIG_INTEL_MEI) += mei/
obj-$(CONFIG_MFD_NVEC) += nvec/
obj-$(CONFIG_DRM_OMAP) += omapdrm/
obj-$(CONFIG_ANDROID) += android/
obj-$(CONFIG_PHONE) += telephony/
obj-$(CONFIG_RAMSTER) += ramster/
obj-$(CONFIG_USB_WPAN_HCD) += ozwpan/
obj-$(CONFIG_PRIMA_WLAN) += prima/
obj-$(CONFIG_PRONTO_WLAN) += prima/
| code |
उत्तराखंड सरकार को राहत : कांग्रेस के बागी विधायकों को नैनीताल हाईकोर्ट से झटका, याचिका खारिज
कांग्रेस के बागी विधायकों को नैनीताल हाईकोर्ट ने जोरदार झटका दिया है। हाईकोर्ट ने बागी विधायकों की याचिका को आधारहीन करार देते हुए खारिज कर दिया है। कोर्ट ने बागियों से कहा कि वे अपना पक्ष विधानसभा में ही रखें। इस फैसले को राज्य की हरीश रावत सरकार के लिए बड़ी राहत माना जा रहा है। अब ये भी माना जा रहा है कि हाईकोर्ट से झटका मिलने के बाद बागी विधायक सुप्रीम कोर्ट से गुहार लगा सकते हैं।
इससे पहले उत्तराखंड का सियासी बवाल शुक्रवार को अचानक हाईकोर्ट तक पहुंच गया। बागी विधायकों ने दो अलग-अलग याचिकाएं दायर कर विधानसभा स्पीकर के नोटिस को चुनौती दी थी। हाईकोर्ट में सरकार की ओर से मशहूर वकील और वरिष्ट काग्रेस नेता कपिल सिब्बल ने पैरवी की।
बागी विधायकों की ओर से नैनीताल हाईकोर्ट में याचिका दाखिल कर स्पीकर गोविंद कुंजवाल की तरफ से दिए गए एंटी डिफेक्शन नोटिस को चुनौती दी गई थी। इस मामले पर जस्टिस सुधांशु धूलिया की कोर्ट में शुक्रवार दोपहर ३ बजे कार्रवाई शुरू हुई और शाम करीब पौने पांच बजे कोर्ट ने बागियों की याचिका खारिज करने का फैसला सुनाया।
बागी विधायकों ने दो अलग-अलग याचिकाएं दाखिल की थी। विधायक अमृता रावत, हरक सिंह रावत, कुंवर प्रणव चैम्पियन और प्रदीप बत्रा ने एक याचिका दाखिल की, जबकि दूसरी याचिका बागी विधायक शैलेंद्र मोहन सिंघल, शैलारानी, सुबोध उनियाल और उमेश शर्मा काऊ ने दाखिल की।
दूसरी याचिका में स्पीकर के नोटिस का जवाब देने के लिए दिए गए सात दिन के समय को कम बताते हुए चुनौती दी गई।
बागियों में से एक और पूर्व कैबिनेट मंत्री हरक सिंह रावत का कहना है कि सभी को अलग-अलग कारण बताओ नोटिस दिया गया था, इसलिए अलग-अलग याचिका लगाई है। उन्होंने कहा कि विधानसभा अध्यक्ष उन्हें सदन के आचरण के लिए नोटिस दे सकते हैं, लेकिन जब अध्यक्ष यह कह रहे हैं कि वित्त विधेयक पास हो गया तो हमने, पार्टी या सरकार के खिलाफ जाकर तो कुछ भी नहीं किया, जिसके लिए हमें नोटिस भेजा गया है।
हरक ने कहा कि हमने अभी कांग्रेस नहीं छोड़ी है। हम सरकार से असंतुष्ट हैं, लेकिन अब भी कांग्रेस के सदस्य हैं। हम पर दलबदल कानून लागू नहीं होता। इस मामले में शुक्रवार दोपहर करीब ३ बजे नैनीताल हाईकोर्ट में सुनवाई तय है। इस बीच बीजेपी के सभी २७ विधायक राजस्थान में पुष्कर पहुंचे हुए हैं। | hindi |
This is the page of currency pairs, Argentine Peso(ARS) convert to Salvadoran Colon(SVC). Below shows the current exchange rate of the currency pairs updated every 1 minutes and their exchange rates history graph. Do you want to INVERT the two currencies? Visit Salvadoran Colon(SVC) to Argentine Peso(ARS). | english |
Below you fill find all funeral homes and cemeteries in or near Eatontown.
Suburbs of Eatontown: Monmouth, Shrewsbury Township, Tinton Falls, Vail Homes.
Zip codes in the city: 07724, 07799.
It was reported by Ann Arbor News on June 8th, 2017 that Howard Voorhees passed away in Ann Arbor, Michigan. Voorhees was 96 years old and was born in Eatontown, NJ. Send flowers to share your condolences and honor Howard's life.
It was reported on February 15th, 2012 that Virginia Marie Miller passed away in Eatontown, New Jersey. Miller was 92 years old. Send flowers to share your condolences and honor Virginia Marie's life.
Eatontown is a Borough (New Jersey) in Monmouth County, New Jersey County, New Jersey, United States. As of the United States 2000 Census, the borough population was 14,008. . . .
A funeral service was held at the John E. Day Funeral Home, Red Bank. Interment was private. Memorial donations may be made to the Juvenile Diabetes Research Foundation, 740 Broad St., Suite 4, Shrewsbury, NJ 07702.
three daughters, Sheila Birmingham of Eatontown, Catharine Birmingham of Manalapan and Mary ... 16 McLean St., Freehold, NJ 07728.
Listing all funeral homes in Eatontown, New Jersey so you can easily send flowers to any location (same day delivery) or find any funeral service.
Find BBB Accredited Funeral Directors near Eatontown, NJ - your guide to trusted Eatontown, NJ Funeral Directors, recommended and BBB Accredited businesses.
Listing all cemeteries in Eatontown, New Jersey so you can easily send flowers to any location (same day delivery) or find any funeral service.
We work with local florists and flower shops to offer same day delivery. You will find budget sympathy flowers in Eatontown here. Our funeral flowers are cheap in price but not in value. | english |
\begin{document}
\title{On the Equivalence of Youla, System-level and Input-output Parameterizations}
\author{Yang Zheng, Luca Furieri, Antonis Papachristodoulou, Na Li, and Maryam Kamgarpour
\thanks{This work is supported by NSF career 1553407, AFOSR Young Investigator Program, and ONR Young Investigator Program. A. Papachristodoulou is supported by the EPSRC Grant EP/M002454/1.
L. Furieri and M. Kamgarpur are gratefully supported by ERC Starting Grant CONENE. }
\thanks{Y. Zheng and N. Li are with SEAS and CGBC, Harvard
University, Cambridge, MA 02138. (E-mails: zhengy@g.harvard.edu; nali@seas.harvard.edu). }
\thanks{L. Furieri and M. Kamgarpour are with the Automatic Control Laboratory, ETH Zurich, Switzerland. (E-mails: \{furieril, mkamgar\}@control.ee.ethz.ch).}
\thanks{A. Papachristodoulou is with the Department of Engineering Science , University of
Oxford, United Kingdom. (E-mail: antonis@eng.ox.ac.uk).
}
}
\maketitle
\begin{abstract}
A convex parameterization of internally stabilizing controllers is fundamental for many controller synthesis procedures. The celebrated Youla parameterization relies on a doubly-coprime factorization of the system, while the recent system-level and input-output characterizations require no doubly-coprime factorization but a set of equality constraints for achievable closed-loop responses. In this paper, we present explicit affine mappings among Youla, system-level and input-output parameterizations. Two direct implications of the affine mappings are 1) any convex problem in Youla, system level, or input-output parameters can be equivalently and convexly formulated in any other one of these frameworks,
including the convex system-level synthesis (SLS); 2) the condition of quadratic invariance (QI) is sufficient and necessary for the classical distributed control problem to admit an equivalent convex reformulation in terms of Youla, system-level, or input-output parameters.
\end{abstract}
\begin{IEEEkeywords}
Stabilizing controller, Youla parameterization, System-level synthesis, Quadratic invariance.
\end{IEEEkeywords}
\section{Introduction}
\label{sec:introduction}
One of the most fundamental problems in control theory is to design a feedback controller that stabilizes a dynamical system. Additionally, one can further design an optimal controller by optimizing a certain performance measure~\cite{zhou1996robust}. It is well-known that the set of stabilizing controllers is in general non-convex, and hence, hard to optimize directly over.
Many optimal controller synthesis procedures first parameterize all stabilizing controllers and the corresponding closed-loop responses in a convex way, and then minimize relevant performance measures over the new parameter(s).
For finite dimensional linear-time-invariant (LTI) systems, the set of LTI stabilizing feedback controllers is fully characterized by the celebrated \emph{Youla parameterization}~\cite{youla1976modern}, where a doubly coprime factorization of the system is used. In~\cite{youla1976modern}, it is shown that the Youla parameterization allows for optimizing the Youla parameter (or system response) directly, instead of the controller itself, leading to a convex problem. Also, customized performance specifications on the closed-loop system can be incorporated with Youla parameterization via convex optimization~\cite{boyd1991linear}. Moreover, the foundational results of robust and optimal control are built on the Youla parameterization~\cite{francis1987course,zhou1996robust}. Note that a doubly-coprime factorization of the system must be computed as a preliminary step in Youla parameterization. Recently, a system-level parameterization~\cite{wang2019system} and an input-output parameterization~\cite{furieri2019input} were introduced to characterize the set of all LTI stabilizing controllers, with no need of computing a doubly-coprime factorization of the system \emph{a priori}. Similar to Youla, the system-level and input-output parameterizations treat certain closed-loop responses as design parameters. The controller synthesis is thus shifted from designing a controller to designing the closed loop responses directly.
This idea of synthesizing closed-loop responses in a convex way was extensively discussed as \emph{closed-loop convexity} in~\cite[Chapter 6]{boyd1991linear}.
The Youla~\cite{youla1976modern}, system-level~\cite{wang2019system}, input-output~\cite{furieri2019input} parameterizations are equivalent since they characterize the same set of stabilizing controllers. However, their explicit relationships have not been fully established before. The main objective of this paper is to reveal an explicit equivalence of Youla, system-level, and input-output parameterizations. In particular, we present explicit \emph{affine mappings} among the Youla parameter, system-level parameters, and input-output parameters. One direct consequence is that any convex problem in terms of Youla, system-level, input-output parameters can be equivalently and convexly formulated into any other one of these three frameworks.
Therefore, the so-called convex system-level synthesis (SLS)~\cite{wang2019system} admits an equivalent convex formulation in terms of Youla or input-output parameters. Another consequence is that if one controller synthesis task does not allow for an equivalent convex reformulation in Youla, a convex reformulation in the system-level or input-output parameterizations is not possible either. Consider the classical distributed controller synthesis task where a subspace constraint is imposed on the controller~\cite{rotkowitz2006characterization}. It has been shown that a notion of quadratic invariance (QI) is sufficient and necessary for the distributed control problem to admit an equivalent convex reformulation in the Youla parameter~\cite{rotkowitz2006characterization,lessard2015convexity}. Accordingly, the QI condition is also sufficient and necessary when using the system-level and input-output parameterizations. For systems with constraints beyond QI, we highlight that a notion of sparsity invariance (SI)~\cite{Furieri2019Sparsity} can be used to derive convex inner-approximations using Youla, system-level, or input-output characterizations.
The rest of this paper is organized as follows. We introduce some preliminaries in Section~\ref{Section:preliminaries}, and review the Youla, system-level, and input-output parameterizations in Section~\ref{Section:paramterization}. Explicit affine relationships and their implication with QI are presented in Section~\ref{Section:equivalence}. We discuss distributed controller synthesis with non-QI constraints in Section~\ref{Section:specialcase}, and conclude the paper in Section~\ref{section:conclusion}.
\noindent\emph{Notation:} We use lower and upper case letters (\emph{e.g.} $x$ and $A$) to denote vectors and matrices, respectively. Lower and upper case boldface letters (\emph{e.g.} $\mathbf{x}$ and $\mathbf{G}$) are used to denote signals and transfer matrices, respectively. For clarity, we consider discrete-time LTI systems only, but unless stated otherwise, all results can be extended to the continuous-time setting. We denote the set of real-rational proper stable transfer matrices as $\mathcal{RH}_{\infty}$. $\mathbf{G} \in \frac{1}{z}\mathcal{RH}_{\infty}$ means $\mathbf{G}$ is stable and strictly proper.
\section{Preliminaries}~\label{Section:preliminaries}
\subsection{System model}
We consider discrete-time LTI systems of the form
\begin{equation} \label{eq:LTI}
\begin{aligned}
{x}[t+1] &= A x[t] + B_1 w[t] + B_2u[t], \\
z[t] &= C_1 x[t] + D_{11}w[t] + D_{12}u[t], \\
y[t] &= C_2x[t] + D_{21}w[t] + D_{22} u[t],
\end{aligned}
\end{equation}
where $x[t],u[t],w[t],y[t],z[t]$ are the state vector, control action, external disturbance, measurement, and regulated output at time $t$, respectively. System~\eqref{eq:LTI} can be written as
$$
\mathbf{P} = \left[ \begin{array}{c|cc} A & B_1 & B_2 \\
\hline
C_1 & D_{11} & D_{12} \\
C_2 & D_{21} & D_{22} \end{array} \right]
= \begin{bmatrix} \mathbf{P}_{11} & \mathbf{P}_{12} \\\mathbf{P}_{21} & \mathbf{P}_{22} \end{bmatrix},
$$
where $\mathbf{P}_{ij} = C_i(zI - A)^{-1}B_j +D_{ij}$. We refer to $\mathbf{P}$ as the open-loop plant model.
Consider a dynamic output feedback controller
$
\mathbf{u} = \mathbf{K}\mathbf{y},
$
where $\mathbf{K}$ has a state space realization
\begin{equation} \label{eq:ControllerLTI}
\begin{aligned}
{\xi}[t+1] &= A_k \xi[t] + B_k y[t], \\
u[t] &= C_k \xi[t] + D_{k}y[t],
\end{aligned}
\end{equation}
with $\xi$ as the internal state of controller $\mathbf{K}$. We have $\mathbf{K} = C_k(zI - A_k)^{-1}B_k + D_k$. Figure~\ref{fig:LTI} shows a schematic diagram of the interconnection of plant $\mathbf{P}$ and controller $\mathbf{K}$. Throughout the paper, we make the following standard assumptions.
\begin{assumption}
Both the plant and controller realizations are stabilizable and detectable, \emph{i.e.}, $(A, B_2)$ and $(A_k, B_k)$ are stabilizable, and $(A,C_2)$ and $(A_k,C_k)$ are detectable.
\end{assumption}
\begin{assumption}
The interconnection in Fig.~\ref{fig:LTI} is well-posed, \emph{i.e.}, $I - D_{22}D_k$ is invertible.
\end{assumption}
\subsection{Stabilization and optimal control}
\begin{definition}
The system in Fig.~\ref{eq:LTI} is \emph{internally stable} if it is well-posed, and the states $(x[t],x_k[t])$ converge to zero as $t\rightarrow \infty$ for all initial states $(x[0],x_k[0])$ when $w[t] = 0, \forall t$.
\end{definition}
We say the controller $\mathbf{K}$ \emph{internally stabilizes} the plant $\mathbf{P}$ if the interconnected system in Fig.~\ref{eq:LTI} is {internally stable}. The set of all stabilizing controllers is defined as
\begin{equation}
\mathcal{C}_{\text{stab}} := \{\mathbf{K} \mid \mathbf{K} \; \text{internally stabilizes} \; \mathbf{P}\}.
\end{equation}
In addition to stability, it is desirable to find a controller $\mathbf{K}$ that minimizes a suitable norm (\emph{e.g.}, $\mathcal{H}_2$ or $\mathcal{H}_{\infty}$) of the closed-loop transfer matrix from $\mathbf{w}$ to $\mathbf{z}$. This amounts to solving the following optimal control formulation~\cite{zhou1996robust}:
\begin{equation} \label{eq:OCP}
\begin{aligned}
\min_{\mathbf{K}} \quad &\|f(\mathbf{P},\mathbf{K})\| \\
\text{subject to} \quad & \mathbf{K} \in \mathcal{C}_{\text{stab}},
\end{aligned}
\end{equation}
where $f(\mathbf{P},\mathbf{K}) = \mathbf{P}_{11} + \mathbf{P}_{12}\mathbf{K}(I - \mathbf{P}_{22}\mathbf{K})^{-1}\mathbf{P}_{21}$. It is known that set $\mathcal{C}_{\text{stab}}$ is non-convex. One can construct explicit examples where $\mathbf{K}_1, \mathbf{K}_2 \in \mathcal{C}_{\text{stab}}$ but $\frac{1}{2}(\mathbf{K}_1+ \mathbf{K}_2) \notin \mathcal{C}_{\text{stab}}$. Also, $f(\mathbf{P},\mathbf{K})$ is in general a non-convex function of $\mathbf{K}$. Therefore, problem~\eqref{eq:OCP} is non-convex in the current form.
\begin{figure}
\caption{Interconnection of the plant $\mathbf{P}
\label{fig:LTI}
\end{figure}
\section{Parameterization of Stabilizing Controllers}\label{Section:paramterization}
To solve the optimal control problem~\eqref{eq:OCP}, one common method is to derive an equivalent convex formulation via a suitable change of variables. A classical technique is the Youla parameterization~\cite{youla1976modern}. Two recent approaches are the so-called system-level parameterization (SLP)~\cite{wang2019system}, and input-output parameterization (IOP)~\cite{furieri2019input}. A common idea among these three approaches is the parameterization of all stabilizing controllers $\mathcal{C}_{\text{stab}}$ using certain closed-loop responses. We review their main results in this section.
\subsection{Youla parameterization}
The classical Youla parameterization is based on a doubly-coprime factorization of the plant $\mathbf{P}_{22}$, defined as follows.
\begin{definition}
A collection of stable transfer matrices, $\mathbf{U}_l, \mathbf{V}_l,\mathbf{N}_l,\mathbf{M}_l,\mathbf{U}_r, \mathbf{V}_r,\mathbf{N}_r,\mathbf{M}_r \in \mathcal{RH_{\infty}}$ is called a doubly-coprime factorization of $\mathbf{P}_{22}$ if
$
\mathbf{P}_{22} = \mathbf{N}_r\mathbf{M}_r^{-1} = \mathbf{M}_l^{-1}\mathbf{N}_l
$
and
$$
\begin{bmatrix} \mathbf{U}_l & -\mathbf{V}_l \\ -\mathbf{N}_l & \mathbf{M}_l\end{bmatrix}
\begin{bmatrix} \mathbf{M}_r & \mathbf{V}_r \\ \mathbf{N}_r & \mathbf{U}_r\end{bmatrix} = I.
$$
\end{definition}
Such doubly-coprime factorizations can always be computed if $\mathbf{P}_{22}$ is stabilizable and detectable~\cite{zhou1996robust}. The authors in~\cite{youla1976modern} established the following equivalence
\begin{equation} \label{eq:youla}
\mathcal{C}_{\text{stab}} = \{\mathbf{K} = (\mathbf{V}_r - \mathbf{M}_r\mathbf{Q})(\mathbf{U}_r - \mathbf{N}_r\mathbf{Q})^{-1} \mid \mathbf{Q} \in \mathcal{RH}_{\infty} \}\footnote{Equivalently, $\mathcal{C}_{\text{stab}}=\{(\mathbf{U}_l-\mathbf{QN}_l)^{-1}(\mathbf{V}_l-\mathbf{QM}_l)|~\mathbf{Q} \in \mathcal{RH}_\infty\}$.},
\end{equation}
where $\mathbf{Q}$ is called the Youla parameter. Using the change of variables
$\mathbf{K} = (\mathbf{V}_r - \mathbf{M}_r\mathbf{Q})(\mathbf{U}_r - \mathbf{N}_r\mathbf{Q})^{-1}$, it is not difficult to derive
$$
f(\mathbf{P},\mathbf{K}) = \mathbf{T}_{11} + \mathbf{T}_{12}\mathbf{Q}\mathbf{T}_{21},
$$
where $\mathbf{T}_{11} = \mathbf{P}_{11} + \mathbf{P}_{12} \mathbf{V}_{r}\mathbf{M}_{l} \mathbf{P}_{21}, \mathbf{T}_{12} = -\mathbf{P}_{12}\mathbf{M}_{r}$, and $\mathbf{T}_{21} = \mathbf{M}_{l}\mathbf{P}_{21}$. Consequently, Problem~\eqref{eq:OCP} can be equivalently reformulated in terms of the Youla parameter as
\begin{equation} \label{eq:OCPYoula}
\begin{aligned}
\min_{\mathbf{Q}} \quad &\|\mathbf{T}_{11} + \mathbf{T}_{12}\mathbf{Q}\mathbf{T}_{21}\| \\
\text{subject to} \quad & \mathbf{Q} \in \mathcal{RH}_{\infty}.
\end{aligned}
\end{equation}
One direct benefit is that~\eqref{eq:OCPYoula} is convex with respect to the Youla parameter $\mathbf{Q}$.
\subsection{System-level parameterization (SLP)}
In~\cite{wang2019system}, the authors proposed a system-level parameterization for $\mathcal{C}_{\text{stab}}$. This approach is based on the closed-loop maps from process and measurement disturbances to state and control action. In particular, assuming a strictly proper plant $\mathbf{P}_{22},$ \emph{i.e.}, $D_{22} = 0$, we use ${\delta_x}[t] = B_1 w[t]$ to denote the disturbance on the state and $\delta_y[t] = D_{21}w[t]$ to denote the disturbance on the measurement. The dynamics of plant~\eqref{eq:LTI} can be written as
\begin{equation*}
\begin{aligned}
{x}[t+1] &= A x[t] + B_2u[t] + \delta_x[t], \\
y[t] &= C_2x[t] + \delta_y[t].
\end{aligned}
\end{equation*}
Then, with a stabilizing controller $\mathbf{u} = \mathbf{K}\mathbf{y}$, the system responses
from perturbations $(\mathbf{\delta_x}, \mathbf{\delta_y})$ to $(\mathbf{x},\mathbf{u})$ are
\begin{equation} \label{eq:LTIsls}
\begin{aligned}
\begin{bmatrix} \mathbf{x} \\\mathbf{u} \end{bmatrix} = \begin{bmatrix} \mathbf{R} & \mathbf{N}\\ \mathbf{M} & \mathbf{L} \end{bmatrix} \begin{bmatrix} \mathbf{\delta_x} \\ \mathbf{\delta_y} \end{bmatrix},
\end{aligned}
\end{equation}
where the system responses $\{\mathbf{R}, \mathbf{M}, \mathbf{N}, \mathbf{L}\}$ are in the following affine subspace~\cite{wang2019system}
\begin{subequations} \label{eq:slp}
\begin{align}
\begin{bmatrix}zI - A & -B_2 \end{bmatrix}\begin{bmatrix} \mathbf{R} & \mathbf{N}\\ \mathbf{M} & \mathbf{L} \end{bmatrix} & = \begin{bmatrix}I & 0\end{bmatrix}, \label{eq:slp_s1}\\
\begin{bmatrix} \mathbf{R} & \mathbf{N}\\ \mathbf{M} & \mathbf{L} \end{bmatrix} \begin{bmatrix}zI - A \\ -C_2 \end{bmatrix} & = \begin{bmatrix}I \\ 0\end{bmatrix}, \label{eq:slp_s2} \\
\mathbf{R}, \mathbf{M}, \mathbf{N} \in \frac{1}{z} \mathcal{RH}_{\infty}, \quad& \mathbf{L} \in \mathcal{RH}_{\infty}. \label{eq:slp_s3}
\end{align}
\end{subequations}
In~\cite{wang2019system}, it is proved that for strictly proper\footnote{The equivalence~\eqref{eq:sls} only holds for strictly proper plants, \emph{i.e.}, $D_{22} = 0$. For a general proper plant $D_{22} \neq 0$, the authors in~\cite{wang2019system} present another controller implementation that internally stabilizes the system; see~\cite[Section III.D]{wang2019system}. Instead, Youla~\eqref{eq:youla} and input-output~\eqref{eq:iop} parameterizations work for both strictly proper and general proper plants. Throughout the paper, we assume a strictly proper plant for the system-level parameterization. } plant $\mathbf{P}_{22}$, the set of all internally stabilizing controllers can be written as
\begin{equation} \label{eq:sls}
\begin{aligned}
\mathcal{C}_{\text{stab}} = \{\mathbf{K} = \mathbf{L} - \mathbf{M}\mathbf{R}^{-1}&\mathbf{N} \mid \mathbf{R}, \, \mathbf{M}, \, \mathbf{N}, \, \mathbf{L} \; \text{are in the } \\
&\text{affine subspace~\eqref{eq:slp_s1}-\eqref{eq:slp_s3}} \}.
\end{aligned}
\end{equation}
Also, the cost function $f(\mathbf{P},\mathbf{K})$ can be expressed in terms of the system responses $\mathbf{R}, \mathbf{M}, \mathbf{N}, \mathbf{L}$. In particular, Problem~\eqref{eq:OCP} can be equivalently reformulated as
\begin{equation} \label{eq:OCPsls}
\begin{aligned}
\min_{\mathbf{R}, \mathbf{M}, \mathbf{N}, \mathbf{L}} \quad &\left\| \begin{bmatrix} C_1 & D_{12} \end{bmatrix}\begin{bmatrix} \mathbf{R} & \mathbf{N}\\ \mathbf{M} & \mathbf{L} \end{bmatrix} \begin{bmatrix} B_1 \\ D_{21} \end{bmatrix} + D_{11} \right\| \\
\text{subject to} \quad & \eqref{eq:slp_s1}-\eqref{eq:slp_s3}.
\end{aligned}
\end{equation}
It is easy to see that~\eqref{eq:OCPsls} is convex in terms of $\mathbf{R}, \mathbf{M}, \mathbf{N}, \mathbf{L}$.
\subsection{Input-output parameterization (IOP)}
\begin{figure}
\caption{Input-output stability.}
\label{fig:IOS}
\end{figure}
Recently, an input-output parameterization for $\mathcal{C}_{\text{stab}}$ was introduced in~\cite{furieri2019input}. As shown in Fig.~\ref{fig:IOS}, the idea is based on a classical internal stability result in terms of the following closed-loop responses
\begin{equation} \label{eq:LTIio}
\begin{aligned}
\begin{bmatrix} \mathbf{y} \\\mathbf{u} \end{bmatrix} = \begin{bmatrix} \mathbf{Y} & \mathbf{W}\\ \mathbf{U} & \mathbf{Z}\end{bmatrix} \begin{bmatrix} \mathbf{\delta_y} \\ \mathbf{\delta_u} \end{bmatrix},
\end{aligned}
\end{equation}
where $\delta_{\mathbf{u}}$ is a disturbance in the input, \emph{i.e.}, $\mathbf{u} = \mathbf{K}y + \delta_{\mathbf{u}}$.
Under Assumption 1, it is known that $\mathbf{K}$ internally stabilizes $\mathbf{P}$ if and only if the four transfer matrices in~\eqref{eq:LTIio} are stable~\cite{francis1987course}. With a stabilizing controller $\mathbf{K}$, the closed-loop responses $\mathbf{Y}, \mathbf{U}, \mathbf{W}, \mathbf{Z}$ are in the following affine subspace~\cite{furieri2019input}
\begin{subequations} \label{Eq:Param}
\begin{align}
&\begin{bmatrix}
I&-\mathbf{P}_{22}
\end{bmatrix}\begin{bmatrix}
\mathbf{Y}&\mathbf{W}\\\mathbf{U}&\mathbf{Z}
\end{bmatrix}=\begin{bmatrix}
I&0
\end{bmatrix}\,, \label{eq:aff1}\\
& \begin{bmatrix}
\mathbf{Y}&\mathbf{W}\\\mathbf{U}&\mathbf{Z}
\end{bmatrix}\begin{bmatrix}
-\mathbf{P}_{22}\\I
\end{bmatrix}=\begin{bmatrix}
0\\I
\end{bmatrix}\label{eq:aff2}\,,\\
&\begin{matrix}
\mathbf{Y}, \mathbf{U}, \mathbf{W}, \mathbf{Z}\in \mathcal{RH}_\infty.
\end{matrix}\label{eq:aff3}
\end{align}
\end{subequations}
It is shown in~\cite{furieri2019input} that the set of all internally stabilizing controllers can be represented as
\begin{equation} \label{eq:iop}
\begin{aligned}
\mathcal{C}_{\text{stab}} = \{\mathbf{K} = \mathbf{U}\mathbf{Y}^{-1} \mid \mathbf{Y}, &\mathbf{U}, \mathbf{W}, \mathbf{Z} \; \text{are in the} \\
&\text{affine subspace~\eqref{eq:aff1}-\eqref{eq:aff3}} \}.
\end{aligned}
\end{equation}
Furthermore, we have $f(\mathbf{P},\mathbf{K}) = \mathbf{P}_{11} + \mathbf{P}_{12}\mathbf{U}\mathbf{P}_{21}$~\cite{furieri2019input}. Accordingly, Problem~\eqref{eq:OCP} can be equivalently reformulated in terms of the system responses as
\begin{equation} \label{eq:OCPiop}
\begin{aligned}
\min_{\mathbf{Y}, \mathbf{U}, \mathbf{W}, \mathbf{Z}} \quad &\left\| \mathbf{P}_{11} + \mathbf{P}_{12}\mathbf{U}\mathbf{P}_{21}\right\| \\
\text{subject to} \quad & ~\eqref{eq:aff1}-\eqref{eq:aff3}.
\end{aligned}
\end{equation}
It is easy to see that~\eqref{eq:OCPiop} is convex in terms of $\mathbf{Y}, \mathbf{U}, \mathbf{W}, \mathbf{Z}$.
\section{Explicit Equivalence of Youla Parameterization, SLP, and IOP}
\label{Section:equivalence}
As discussed in the last section, the set of all stabilizing controllers $\mathcal{C}_{\text{stab}}$ can be parameterized in three different ways, \emph{i.e.},~\eqref{eq:youla},~\eqref{eq:sls}, and~\eqref{eq:iop}, and the optimal control problem~\eqref{eq:OCP} admits three equivalent convex reformulations, \emph{i.e.},~\eqref{eq:OCPYoula},~\eqref{eq:OCPsls}, and~\eqref{eq:OCPiop}. Implicitly,~\eqref{eq:youla},~\eqref{eq:sls}, and~\eqref{eq:iop} are equivalent. However, an explicit relationship between Youla parameterization, SLP, and IOP is not clear from their definitions.
In this section, we present explicit \emph{affine mappings} among Youla parameterization, SLP, and IOP. The consequences are as follows: 1) any convex system-level synthesis (SLS) introduced by~\cite{wang2019system} can be equivalently reformulated into a convex problem in terms of the Youla parameter $\mathbf{Q}$ or the input-output parameters $\mathbf{Y}, \mathbf{U}, \mathbf{W}, \mathbf{Z}$, and vice versa; 2) building on the explicit affine mappings, we show that the notion of quadratic invariance~\cite{rotkowitz2006characterization} allows for equivalent convex reformulations of classical distributed optimal control in either Youla parameterization, SLP, or IOP.
\subsection{Explicit equivalence}
The explicit equivalence between Youla parameterization and IOP is presented in~\cite{furieri2019input}:
\begin{theorem}[\!\cite{furieri2019input}]
\label{th:Youla_eq}
Let $\mathbf{U}_r,\mathbf{V}_r,\mathbf{U}_l,\mathbf{V}_l,\mathbf{M}_r,\mathbf{M}_l,\mathbf{N}_r,\mathbf{N}_l$ be any doubly-coprime factorization of $\mathbf{P}_{22}$. The following statements hold.
\begin{enumerate}
\item For any $\mathbf{Q} \in \mathcal{RH}_\infty$, the following transfer matrices
\begin{subequations} \label{eq:youla_iop}
\begin{align}
&\mathbf{Y}=(\mathbf{U}_r-\mathbf{N}_r\mathbf{Q})\mathbf{M}_l\,, \label{eq:Q_to_X_1}\\
&\mathbf{U}=(\mathbf{V}_r-\mathbf{M}_r\mathbf{Q})\mathbf{M}_l\,,\\
&\mathbf{W}=(\mathbf{U}_r-\mathbf{N}_r\mathbf{Q})\mathbf{N}_l\,,\\
&\mathbf{Z}=I+(\mathbf{V}_r-\mathbf{M}_r\mathbf{Q})\mathbf{N}_l\,,\label{eq:Q_to_X_2}
\end{align}
\end{subequations}
belong to the affine subspace \eqref{eq:aff1}-\eqref{eq:aff3} and are such that $\mathbf{U}\mathbf{Y}^{-1}=(\mathbf{V}_r-\mathbf{M}_r\mathbf{Q})(\mathbf{U}_r-\mathbf{N}_r\mathbf{Q})^{-1}$.
\item For any $(\mathbf{Y},\mathbf{U},\mathbf{W},\mathbf{Z})$ in the affine subspace (\ref{eq:aff1})-(\ref{eq:aff3}), the transfer matrix
\begin{equation}
\label{eq:Youla_with_XYWZ}
\mathbf{Q}=\mathbf{V}_l\mathbf{Y}\mathbf{U}_r-\mathbf{U}_l\mathbf{U}\mathbf{U}_r-\mathbf{V}_l\mathbf{W}\mathbf{V}_r+\mathbf{U}_l\mathbf{Z}\mathbf{V}_r-\mathbf{V}_l\mathbf{U}_r\,,
\end{equation}
is such that $\mathbf{Q} \in \mathcal{RH}_\infty$ and $(\mathbf{V}_r-\mathbf{M}_r\mathbf{Q})(\mathbf{U}_r-\mathbf{N}_r\mathbf{Q})^{-1}=\mathbf{U}\mathbf{Y}^{-1}$.
\end{enumerate}
\end{theorem}
Theorem~\ref{th:Youla_eq} presents explicit {affine mappings} between Youla parameterization and IOP: {any element in the Youla parameterization~\eqref{eq:youla} corresponds to an element in the IOP~\eqref{eq:iop}, and they represent the same controller.} The following result presents explicit {affine mappings} between SLP and IOP.
\begin{theorem}
\label{th:slp_eq}
Consider a strictly proper plant $\mathbf{P}_{22}$, \emph{i.e.}, $D_{22} = 0$. The following statements hold.
\begin{enumerate}
\item For any $\mathbf{R}, \mathbf{M}, \mathbf{N}, \mathbf{L}$ satisfying the affine subspace~\eqref{eq:slp_s1}-\eqref{eq:slp_s3}, the transfer matrices
\begin{subequations} \label{eq:slp-iop}
\begin{align}
\mathbf{Y} &= C_2\mathbf{N} + I, \label{eq:slp-iop1}\\
\mathbf{U} &= \mathbf{L}, \label{eq:slp-iop2}\\
\mathbf{W} &= C_2\mathbf{R}B_2, \label{eq:slp-iop3}\\
\mathbf{Z} &= \mathbf{M}B_2 + I, \label{eq:slp-iop4}
\end{align}
\end{subequations}
belong to the affine subspace~\eqref{eq:aff1}-\eqref{eq:aff3} and are such that
$
\mathbf{L} - \mathbf{M}\mathbf{R}^{-1}\mathbf{N} = \mathbf{U}\mathbf{Y}^{-1}.
$
\item For any $\mathbf{Y}, \mathbf{U}, \mathbf{W}, \mathbf{Z}$ satisfying the affine subspace~\eqref{eq:aff1}-\eqref{eq:aff3}, the transfer matrices
\begin{subequations} \label{eq:iop-sls}
\begin{align}
\mathbf{R} &= (zI - A)^{-1} + (zI - A)^{-1}B_2\mathbf{U}C_2(zI - A)^{-1} \label{eq:iop-sls1} \\
\mathbf{M} & = \mathbf{U}C_2(zI - A)^{-1}, \label{eq:iop-sls2}\\
\mathbf{N} &= (zI - A)^{-1}B_2\mathbf{U}, \label{eq:iop-sls3} \\
\mathbf{L} &= \mathbf{U}, \label{eq:iop-sls4}
\end{align}
\end{subequations}
belong to the affine subspace~\eqref{eq:slp_s1}-\eqref{eq:slp_s3} and are such that
$
\mathbf{U}\mathbf{Y}^{-1} = \mathbf{L} - \mathbf{M}\mathbf{R}^{-1}\mathbf{N}.
$
\end{enumerate}
\end{theorem}
\begin{proof}
\emph{Statement 1}: considering the affine relationships~\eqref{eq:slp_s1}-\eqref{eq:slp_s3} and $\mathbf{P}_{22} = C_2(zI - A)^{-1}B_2$, we have the following algebraic equalities:
$$
\begin{aligned}
\mathbf{Y} - \mathbf{P}_{22}\mathbf{U} &= C_2\mathbf{N} + I - \mathbf{P}_{22}\mathbf{L} \\
&= C_2(\mathbf{N} - (zI - A)^{-1}B_2\mathbf{L}) + I = I, \\
\mathbf{W} - \mathbf{P}_{22}\mathbf{Z} &= C_2\mathbf{R}B_2 - \mathbf{P}_{22}( \mathbf{M}B_2 + I) \\
&= C_2\left(\mathbf{R} - (zI - A)^{-1}B_2\mathbf{M} -(zI - A)^{-1}\right)B_2 \\
&= 0, \\
\mathbf{Y}\mathbf{P}_{22} - \mathbf{W} &= (C_2\mathbf{N} + I)\mathbf{P}_{22} - C_2\mathbf{R}B_2 \\
&= C_2\left( \mathbf{N}C_2(zI - A)^{-1} + (zI - A)^{-1} - \mathbf{R}\right)B_2 \\
&= 0,\\
\end{aligned}
$$
$$
\begin{aligned}
-\mathbf{U}\mathbf{P}_{22} + \mathbf{Z} &= -\mathbf{L}\mathbf{P}_{22} + \mathbf{M}B_2 + I \\
& = (-\mathbf{L}C_2(zI-A)^{-1} + \mathbf{M})B_2 + I \\
&= I.
\end{aligned}
$$
Therefore,~\eqref{eq:aff1} and~\eqref{eq:aff2} are satisfied. Obviously, the transfer matrices in~\eqref{eq:slp-iop} are stable, \emph{i.e.}~\eqref{eq:aff3} is satisfied.
In addition, from~\eqref{eq:slp_s2}, we have $\mathbf{R} = (I + \mathbf{N}C_2)(zI - A)^{-1}$. Then,
$$
\begin{aligned}
\mathbf{L} - \mathbf{M}\mathbf{R}^{-1}\mathbf{N} &= \mathbf{L} - \mathbf{M}(zI - A)(I + \mathbf{N}C_2)^{-1}\mathbf{N} \\
&= \mathbf{L} - \mathbf{L}C_2(I + \mathbf{N}C_2)^{-1}\mathbf{N} \\
&= \mathbf{L} - \mathbf{L}C_2\mathbf{N}(I + C_2\mathbf{N})^{-1} \\
& = \mathbf{L}(I + C_2\mathbf{N})^{-1} \\
& = \mathbf{U}\mathbf{Y}^{-1}.
\end{aligned}
$$
\emph{Statement 2}:
In the Appendix~\ref{Sec:stable}, we verify algebraically that the transfer matrices $\mathbf{R},\mathbf{M},\mathbf{N},\mathbf{L}$ defined in~\eqref{eq:iop-sls} are exactly the closed-loop responses in~\eqref{eq:LTIsls} with controller $\mathbf{K} = \mathbf{U}\mathbf{Y}^{-1}$.
Since $\mathbf{K} = \mathbf{U}\mathbf{Y}^{-1}$ is internally stabilizing $\mathbf{P}_{22}$, the transfer matrices $\mathbf{R},\mathbf{M},\mathbf{N},\mathbf{L}$ defined in~\eqref{eq:iop-sls} naturally satisfy the constraints~\eqref{eq:slp_s1}-\eqref{eq:slp_s3}.
Finally, we can check that the transfer matrices $\mathbf{R},\mathbf{M},\mathbf{N}, \mathbf{L}$ defined in~\eqref{eq:iop-sls} satisfy
$
\mathbf{U}\mathbf{Y}^{-1} = \mathbf{L} - \mathbf{M}\mathbf{R}^{-1}\mathbf{N}.
$
This completes the proof.
\end{proof}
Combining Theorems~\ref{th:Youla_eq} and~\ref{th:slp_eq}, we arrive at the explicit affine mappings between Youla parameterization and SLP, which was not provided in~\cite{wang2019system}.
\begin{theorem}
\label{th:Youla_sls}
Let $\mathbf{U}_r,\mathbf{V}_r,\mathbf{U}_l,\mathbf{V}_l,\mathbf{M}_r,\mathbf{M}_l,\mathbf{N}_r,\mathbf{N}_l$ be any doubly-coprime factorization of the strictly proper system $\mathbf{P}_{22}$. The following statements hold.
\begin{enumerate}
\item For any $\mathbf{Q} \in \mathcal{RH}_\infty$, the following transfer matrices
\begin{subequations} \label{eq:youla_slp}
\begin{align}
\mathbf{R} &= (zI - A)^{-1} + \nonumber\\
(zI - &A)^{-1}B_2(\mathbf{V}_r-\mathbf{M}_r\mathbf{Q})\mathbf{M}_lC_2(zI - A)^{-1}, \label{eq:youla_slp1} \\
\mathbf{M} & = (\mathbf{V}_r-\mathbf{M}_r\mathbf{Q})\mathbf{M}_lC_2(zI - A)^{-1}, \label{eq:youla_slp2}\\
\mathbf{N} &= (zI - A)^{-1}B_2(\mathbf{V}_r-\mathbf{M}_r\mathbf{Q})\mathbf{M}_l, \label{eq:youla_slp3}\\
\mathbf{L} &= (\mathbf{V}_r-\mathbf{M}_r\mathbf{Q})\mathbf{M}_l, \label{eq:youla_slp4}
\end{align}
\end{subequations}
belong to the affine subspace \eqref{eq:slp_s1}-\eqref{eq:slp_s3} and are such that $\mathbf{L} - \mathbf{M}\mathbf{R}^{-1}\mathbf{N}=(\mathbf{V}_r-\mathbf{M}_r\mathbf{Q})(\mathbf{U}_r-\mathbf{N}_r\mathbf{Q})^{-1}$.
\item For any $(\mathbf{R},\mathbf{M},\mathbf{N},\mathbf{L})$ in the affine subspace \eqref{eq:slp_s1}-\eqref{eq:slp_s3}, the transfer matrix
\begin{equation} \label{eq:Youla_with_RMNL}
\begin{aligned}
\mathbf{Q} =&\mathbf{V}_lC_2\mathbf{N}\mathbf{U}_r-\mathbf{U}_l\mathbf{L}\mathbf{U}_r-\mathbf{V}_l C_2\mathbf{R}B_2\mathbf{V}_r \\
& \qquad \qquad \qquad \qquad +\mathbf{U}_l\mathbf{M}B_2\mathbf{V}_r + \mathbf{U}_l\mathbf{V}_r
\end{aligned}
\end{equation}
is such that $\mathbf{Q} \in \mathcal{RH}_\infty$ and $(\mathbf{V}_r-\mathbf{M}_r\mathbf{Q})(\mathbf{U}_r-\mathbf{N}_r\mathbf{Q})^{-1}=\mathbf{L} - \mathbf{M}\mathbf{R}^{-1}\mathbf{N}$.
\end{enumerate}
\end{theorem}
\begin{proof}
Statement 1 directly follows by combining the statement 1 of Theorem~\ref{th:Youla_eq} with the statement 2 of Theorem~\ref{th:slp_eq}.
Combining the statement 2 of Theorem~\ref{th:Youla_eq} with the statement 1 of Theorem~\ref{th:slp_eq} leads to
\begin{equation*}
\begin{aligned}
\mathbf{Q} &=\mathbf{V}_l(C_2\mathbf{N} + I)\mathbf{U}_r-\mathbf{U}_l\mathbf{L}\mathbf{U}_r-\mathbf{V}_l C_2\mathbf{R}B_2\mathbf{V}_r \\
& \qquad +\mathbf{U}_l(\mathbf{M}B_2 + I)\mathbf{V}_r-\mathbf{V}_l\mathbf{U}_r\,, \\
&=\mathbf{V}_lC_2\mathbf{N}\mathbf{U}_r-\mathbf{U}_l\mathbf{L}\mathbf{U}_r-\mathbf{V}_l C_2\mathbf{R}B_2\mathbf{V}_r \\
& \qquad +\mathbf{U}_l\mathbf{M}B_2\mathbf{V}_r + \mathbf{U}_l\mathbf{V}_r.
\end{aligned}
\end{equation*}
This completes the proof.
\end{proof}
An overview of the equivalence of Youla parameterization, SLP, and IOP is shown in Fig.~\ref{Fig:Equivalence}.
\begin{remark}[Closed-loop convexity]
In both SLP and IOP, the parameters $(\mathbf{R},\mathbf{M},\mathbf{N},\mathbf{L})$ and $(\mathbf{Y},\mathbf{U},\mathbf{W},\mathbf{Z})$ have explicit and distinct physical interpretations as corresponding closed-loop transfer matrices. Also, the Youla parameter $\mathbf{Q}$ can be viewed as a closed-loop transfer matrix when the plant $\mathbf{P}_{22}$ is stable (see Remark~\ref{remark:stableQ}). In this sense, Youla parameterization, SLP, and IOP all shift the controller synthesis task from the design of a controller in~\eqref{eq:OCP}, which is non-convex, to the design of closed loop responses, resulting in convex formulations~\eqref{eq:OCPYoula},~\eqref{eq:OCPsls}, and~\eqref{eq:OCPiop}. Note that this idea of closed-loop convexity has been extensively discussed in the book~\cite{boyd1991linear}, and a comprehensive historical note is given in~\cite[Chapter 16.3]{boyd1991linear}.
\end{remark}
\begin{remark}[Numerical computation]
After computing a doubly-coprime factorization of the plant, the Youla parameter $\mathbf{Q}$ is free in $\mathcal{RH}_{\infty}$ for parameterizing $\mathcal{C}_{\emph{\text{stab}}}$, and there are no equality constraints for achievable closed-loop responses. This feature allows to reformulate Problem~\eqref{eq:OCP} as a model matching problem~\eqref{eq:OCPYoula}, which can be reduced to the Nehari problem and then solved via the state-space method in~\cite{francis1987course}. Instead, both SLP and IOP do not require to compute a doubly-coprime factorization, but have explicit affine constraints for achievable closed-loop responses.
Since the decision variables in constraints \eqref{eq:slp_s1}-\eqref{eq:slp_s3} and~\eqref{eq:aff1}-\eqref{eq:aff3} are infinite dimensional, there is no immediately efficient numerical method for solving~\eqref{eq:OCPsls} or~\eqref{eq:OCPiop}. The Ritz approximation~\cite[Chapter 15]{boyd1991linear} is one method for solving infinite dimensional optimization problems. Specifically, for discrete-time systems, the finite impulse response (FIR) approximation is a practical choice~\cite{wang2019system,furieri2019input}.
\end{remark}
\begin{figure}
\caption{Equivalence of Youla paramterization, System-level parameterization (SLP), and Input-output parameterization (IOP).}
\label{Fig:Equivalence}
\end{figure}
\subsection{Convex system-level synthesis}
In~\cite{wang2019system}, the authors introduced a general framework of system-level synthesis (SLS), which defines ``the broadest
known class of constrained optimal control problems that can be solved using convex programming'' (cf.~\cite{anderson2019system}).
Thanks to the full equivalence in Theorems~\ref{th:Youla_eq}-\ref{th:Youla_sls}, we can show that 1) any SLS problem can be equivalently formulated in the Youla or input-output framework, 2) any convex SLS can be addressed by solving a convex problem in terms of Youla parameter $\mathbf{Q}$ or input-output parameters $\mathbf{Y}, \mathbf{U}, \mathbf{W}, \mathbf{Z}$.
Let $g(\cdot)$ be a functional capturing a desired measure of the performance of the plant $\mathbf{P}_{22}$, and let $\mathcal{S}$ be a system-level constraint. The SLS problem in~\cite{wang2019system} is posed as
\begin{equation} \label{eq:slsproblem}
\begin{aligned}
\min_{\mathbf{R}, \mathbf{M}, \mathbf{N}, \mathbf{L}} \quad & g(\mathbf{R}, \mathbf{M}, \mathbf{N}, \mathbf{L}) \\
\text{subject to} \quad & \eqref{eq:slp_s1}-\eqref{eq:slp_s3}, \\
& \begin{bmatrix} \mathbf{R} & \mathbf{N} \\
\mathbf{M} & \mathbf{L} \end{bmatrix} \in \mathcal{S}.
\end{aligned}
\end{equation}
We refer the interested reader to~\cite{wang2019system} for a detailed discussion of SLS. Then, we have the following result.
\begin{theorem} \label{theo:equivalence}
Let $\mathbf{U}_r,\mathbf{V}_r,\mathbf{U}_l,\mathbf{V}_l,\mathbf{M}_r,\mathbf{M}_l,\mathbf{N}_r,\mathbf{N}_l$ be any doubly-coprime factorization of the strictly proper system $\mathbf{P}_{22}$. The following statements hold.
\begin{enumerate}
\item The SLS problem~\eqref{eq:slsproblem} is equivalent to the following problem in Youla parameter $\mathbf{Q}$,
\begin{equation} \label{eq:sls-youla}
\begin{aligned}
\min_{\mathbf{Q}} \quad\; & g_1(\mathbf{Q}) \\
\text{subject to} \quad & \begin{bmatrix} f_1(\mathbf{Q}) & f_3(\mathbf{Q}) \\
f_2(\mathbf{Q}) & f_4(\mathbf{Q}) \end{bmatrix} \in \mathcal{S},
\end{aligned}
\end{equation}
where $f_1(\mathbf{Q}), f_2(\mathbf{Q}), f_3(\mathbf{Q}), f_4(\mathbf{Q})$ are defined by~\eqref{eq:youla_slp1} -\eqref{eq:youla_slp4}, respectively, and $$
g_1(\mathbf{Q}) := g\left(f_1(\mathbf{Q}), f_2(\mathbf{Q}), f_3(\mathbf{Q}), f_4(\mathbf{Q})\right).
$$
\item The SLS problem~\eqref{eq:slsproblem} is equivalent to the following problem in input-output parameters $\mathbf{Y}, \mathbf{U}, \mathbf{W}, \mathbf{Z}$,
\begin{equation} \label{eq:sls-iop}
\begin{aligned}
\min_{\mathbf{Y},\mathbf{U},\mathbf{W},\mathbf{Z}} \quad\; & \hat{g}_1(\mathbf{U}) \\
\text{subject to} \quad & ~\eqref{eq:aff1}-\eqref{eq:aff3}\\
\quad &\begin{bmatrix} \hat{f}_1(\mathbf{U}) & \hat{f}_3(\mathbf{U}) \\
\hat{f}_2(\mathbf{U}) & \hat{f}_4(\mathbf{U}) \end{bmatrix} \in \mathcal{S},
\end{aligned}
\end{equation}
where $\hat{f}_1(\mathbf{U}), \hat{f}_2(\mathbf{U}), \hat{f}_3(\mathbf{U}), \hat{f}_4(\mathbf{U})$ are defined by~\eqref{eq:iop-sls1} -\eqref{eq:iop-sls4}, respectively, and $$
\hat{g}_1(\mathbf{U}) := g\left(\hat{f}_1(\mathbf{U}), \hat{f}_2(\mathbf{U}), \hat{f}_3(\mathbf{U}), \hat{f}_4(\mathbf{U})\right).
$$
\item If the SLS problem~\eqref{eq:slsproblem} is convex, then Problems~\eqref{eq:sls-youla} and~\eqref{eq:sls-iop} are both convex.
\end{enumerate}
\end{theorem}
\begin{proof}
The first two statements directly follow from Theorems~\ref{th:slp_eq} and~\ref{th:Youla_sls}.
The last statement follows from the facts that $f_i(\mathbf{Q})$ and $\hat{f}_i(\mathbf{Q}), i = 1, \ldots, 4$, are all affine. Then, if $\mathcal{S}$ is a convex set and $g(\cdot)$ is a convex functional, the constraint in~\eqref{eq:sls-youla} (resp. ~\eqref{eq:sls-iop}) defines a convex set in $\mathbf{Q}$ (resp. $\mathbf{Y}, \mathbf{U}, \mathbf{W}, \mathbf{Z}$), and $g_1(\cdot)$ (or $\hat{g}_1(\cdot)$) is convex.
\end{proof}
\subsection{Distributed optimal control and quadratic invariance (QI)}
Unlike SLS, which impose constraints on closed-loop responses (see~\eqref{eq:slsproblem}), the classical distributed optimal control problem typically considers a subspace constraint $\mathcal{L}$ on the controller $\mathbf{K}$, which is formulated as~\cite{rotkowitz2006characterization, sabuau2014youla, qi2004structured}
\begin{equation} \label{eq:OCPsparsity}
\begin{aligned}
\min_{\mathbf{K}} \quad &\|f(\mathbf{P},\mathbf{K})\| \\
\text{subject to} \quad & \mathbf{K} \in \mathcal{C}_{\text{stab}} \cap \mathcal{L}.
\end{aligned}
\end{equation}
It is shown in~\cite{rotkowitz2006characterization, sabuau2014youla} that if the subspace constraint $\mathcal{L}$ is \emph{quadratically invariant} (QI) under $\mathbf{P}_{22}$ (\emph{i.e.}, $\mathbf{K}\mathbf{P}_{22}\mathbf{K} \in \mathcal{L}, \forall \mathbf{K} \in \mathcal{L}$), then we have
$$
\begin{aligned}
\mathcal{C}_{\text{stab}} \cap \mathcal{L} = \{\mathbf{K} = &(\mathbf{V}_r - \mathbf{M}_r\mathbf{Q})(\mathbf{U}_r - \mathbf{N}_r\mathbf{Q})^{-1} \mid \\
& (\mathbf{V}_r-\mathbf{M}_r\mathbf{Q})\mathbf{M}_l \in \mathcal{L}, \mathbf{Q} \in \mathcal{RH}_{\infty}\}.
\end{aligned}
$$
Problem~\eqref{eq:OCPsparsity} can thus be equivalently formulated as a convex problem in $\mathbf{Q}$~\cite{rotkowitz2006characterization, sabuau2014youla},
\begin{equation} \label{eq:OCPYoula_sparsity}
\begin{aligned}
\min_{\mathbf{Q}} \quad &\|\mathbf{T}_{11} + \mathbf{T}_{12}\mathbf{Q}\mathbf{T}_{21}\| \\
\text{subject to} \quad & (\mathbf{V}_r-\mathbf{M}_r\mathbf{Q})\mathbf{M}_l \in \mathcal{L}, \\
& \mathbf{Q} \in \mathcal{RH}_{\infty}.
\end{aligned}
\end{equation}
Considering the equivalence shown in Theorems~\ref{th:Youla_eq} and~\ref{th:Youla_sls}, the following corollaries are immediate.
\begin{corollary}[QI with IOP]
\label{prop:iop_structured}
If $\mathcal{L}$ is QI under $\mathbf{P}_{22}$, then
\begin{enumerate}
\item We have $$
\begin{aligned}
\mathcal{C}_{\text{stab}} \cap \mathcal{L} = \{\mathbf{K} = &\mathbf{U}\mathbf{Y}^{-1} \mid \mathbf{Y}, \mathbf{U}, \mathbf{W}, \mathbf{Z} \; \text{are in the} \\
&\quad\text{affine subspace~\eqref{eq:aff1}-\eqref{eq:aff3}}, \mathbf{U} \in \mathcal{L} \}.
\end{aligned}
$$
\item Problem~\eqref{eq:OCPsparsity} can be equivalently formulated as a convex problem
\begin{equation} \label{eq:OCPiop_s}
\begin{aligned}
\min_{\mathbf{Y}, \mathbf{U}, \mathbf{W}, \mathbf{Z}} \quad &\left\| \mathbf{P}_{11} + \mathbf{P}_{12}\mathbf{U}\mathbf{P}_{21}\right\| \\
\text{subject to} \quad &\eqref{eq:aff1}-\eqref{eq:aff3}, \\
& \; \mathbf{U} \in \mathcal{L}.
\end{aligned}
\end{equation}
\end{enumerate}
\end{corollary}
\begin{corollary}[QI with SLA] \label{prop:sls_structured}
If $\mathcal{L}$ is QI under $\mathbf{P}_{22}$, then
\begin{enumerate}
\item We have $$
\begin{aligned}
\mathcal{C}_{\text{stab}} \cap \mathcal{L} = \{\mathbf{K} &= \mathbf{L} - \mathbf{M}\mathbf{R}^{-1}\mathbf{N} \mid \mathbf{R}, \, \mathbf{M}, \, \mathbf{N}, \, \mathbf{L} \; \text{are } \\
&\text{in the affine subspace~\eqref{eq:slp_s1}-\eqref{eq:slp_s3}}, \mathbf{L} \in \mathcal{L} \}.
\end{aligned}
$$
\item Problem~\eqref{eq:OCPsparsity} can be equivalently formulated as a convex problem
\end{enumerate}
\begin{equation} \label{eq:OCPiop_s}
\begin{aligned}
\min_{\mathbf{R}, \mathbf{M}, \mathbf{N}, \mathbf{L}} \quad &\left\| \begin{bmatrix} C_1 & D_{12} \end{bmatrix}\begin{bmatrix} \mathbf{R} & \mathbf{N}\\ \mathbf{M} & \mathbf{L} \end{bmatrix} \begin{bmatrix} B_1 \\ D_{21} \end{bmatrix} + D_{11}\right\| \\
\text{subject to} \quad & \eqref{eq:slp_s1}-\eqref{eq:slp_s3}, \\
& \mathbf{L} \in \mathcal{L}.
\end{aligned}
\end{equation}
\end{corollary}
Corollary~\ref{prop:iop_structured} is the same as Theorem~3 of \cite{furieri2019input} and Corollary~\ref{prop:sls_structured} is consistent with Theorem 3 of~\cite{wang2019system}.
One main insight is that the specialized proofs in \cite{furieri2019input,wang2019system} may be not needed anymore, thanks to the explicit affine mappings between Youla, SLP and IOP.
We also note that the original proof of Theorem 3 in~\cite{wang2019system} is not complete: it relies on that the affine mapping $\mathbf{L} = (\mathbf{V}_r-\mathbf{M}_r\mathbf{Q})\mathbf{M}_l$ is invertible. However, given $\mathbf{L} \in \mathcal{RH}_{\infty}$, it is not immediate to see that $\mathbf{Q} = \mathbf{M}_r^{-1}(\mathbf{V}_r-\mathbf{L}\mathbf{M}_r^{-1})$ is stable. We complete this fact via the construction of $\mathbf{Q}$ in~\eqref{eq:Youla_with_RMNL}.
\begin{remark}
It should be noted that SLS~\eqref{eq:slsproblem} and the classical distributed control problem~\eqref{eq:OCPsparsity} are two distinct formulations: 1) the former imposes constraints on closed-loop responses while the latter imposes a constraint on controller $\mathbf{K}$; 2) feasibility of the former does not imply feasibility of the latter, and vice-versa. Only when the QI property holds, can Problem~\eqref{eq:OCPsparsity} be equivalently reformulated into a convex problem in terms of Youla, system-level, or input-output parameters. Based on the results in~\cite{lessard2015convexity}, QI is necessary for the existence of such equivalent convex reformulation. For systems with QI constraints, SLS~\eqref{eq:slsproblem} can be equivalent to the classical problem~\eqref{eq:OCPsparsity}, as shown in Corollary~\ref{prop:sls_structured}; for the cases beyond QI, they are not directly comparable.
\end{remark}
\section{Distributed optimal control with non-QI constraints}
\label{Section:specialcase}
In this section, we highlight that for systems with non-QI constraints, we may derive convex approximations of~\eqref{eq:OCPsparsity} using Youla, system-level, or input-output parameters. In certain cases, a globally optimal solution can still be obtained. Our approximation procedure is consistent with the idea of sparsity invariance (SI)~\cite{Furieri2019Sparsity}.
In particular, we consider Example 1 in~\cite{wang2019system, anderson2019system}. We first present simplified versions of Youla, system-level, and input-output parameterizations for special cases of state feedback (for completeness, other simplified versions for stable plants are presented in Appendix~\ref{section:special}). Then, we show that Example 1 can be solved exactly using Youla, system-level, or input-output parameters via convex optimization.
\subsection{Simplified parameterizations for state feedback}
In~\cite{wang2019system}, it is shown that for state feedback where $C_2 = I, D_{22} = 0$, the set of internally stabilizing controllers is
\begin{equation} \label{eq:slp-stable-state}
\begin{aligned}
\mathcal{C}_{\text{stab}} = \{\mathbf{K} = \mathbf{M}\mathbf{R}^{-1} \bigm| & \begin{bmatrix} (zI -A) & -B_2 \end{bmatrix} \begin{bmatrix} \mathbf{R} \\ \mathbf{M} \end{bmatrix} = I, \\
&\qquad \qquad \mathbf{M},\mathbf{R} \in \frac{1}{z}\mathcal{RH}_{\infty}
\}.
\end{aligned}
\end{equation}
The proof in~\cite{wang2019system} is directly based on the definition of internal stability. As expected, this special case~\eqref{eq:slp-stable-state} can be reduced from the general case~\eqref{eq:sls} from purely algebraic operations. We provide this alternative proof in Appendix~\ref{section:proofB}.
For IOP and Youla parameterization, simplifications are possible with further assumptions.
\begin{corollary}[Input-output parameterization] \label{coro:iopstate}
Suppose $C_2 = I, D_{22}= 0$ and $B_2$ is invertible. We have
\begin{equation} \label{eq:iop-state}
\begin{aligned}
\mathcal{C}_{\text{stab}} = \bigg\{\mathbf{K} = (\mathbf{Z}-I)&\mathbf{W}^{-1} \bigm|
\begin{bmatrix} I & -\mathbf{P}_{22} \end{bmatrix} \begin{bmatrix} \mathbf{W} \\ \mathbf{Z} \end{bmatrix} = 0 \\ & \mathbf{Z} \in \mathcal{RH}_{\infty}, \mathbf{W} \in \frac{1}{z}\mathcal{RH}_{\infty}\bigg\}.
\end{aligned}
\end{equation}
\end{corollary}
\begin{proof}
We show that any controller in~\eqref{eq:iop-state} is an internally stabilizing controller in~\eqref{eq:iop}. The other direction is similar. Given any $\mathbf{W}, \mathbf{Z}$ satisfying the constraints in~\eqref{eq:iop-state}, we define
$
\mathbf{U} = (\mathbf{Z}-I)B_2^{-1}(zI - A) \in \mathcal{RH}_{\infty},
\mathbf{Y} = \mathbf{W}B_2^{-1}(zI - A) \in \mathcal{RH}_{\infty}.
$
Then, we can easily verify
$$
\begin{aligned}
\mathbf{Z}-\mathbf{U}\mathbf{P}_{22} = I, \mathbf{W}-\mathbf{Y}\mathbf{P}_{22} = 0,
\mathbf{Y}-\mathbf{P}_{22}\mathbf{U} = I.
\end{aligned}
$$
Thus, $\mathbf{Y},\mathbf{U},\mathbf{W},\mathbf{Z} $ above satisfy~\eqref{eq:aff1}-\eqref{eq:aff3}.
We also have
$$
\begin{aligned}
\mathbf{U}\mathbf{Y}^{-1} &= (\mathbf{Z}-I)B_2^{-1}(zI - A)(\mathbf{W}B_2^{-1}(zI - A))^{-1} \\
&= (\mathbf{Z}-I)\mathbf{W}^{-1}.
\end{aligned}
$$
This completes the proof.
\end{proof}
\begin{corollary}[Youla parameterization]
\label{Corollary:YoulaState}
Suppose $C_2 = B_2 = I, D_{22} = 0$. We have\footnote{Note that Corollary~\ref{Corollary:YoulaState} is only valid in discrete-time systems, since the doubly-coprime factorization~\eqref{eq:YoulaCo_state} has no counterpart in continuous time.}
$$
\begin{aligned}
\mathcal{C}_{\text{stab}} = \bigg\{\mathbf{K} = \left(-A - (I- \frac{1}{z}A)\mathbf{Q}\right)&\left(I - \frac{1}{z}\mathbf{Q}\right)^{-1}, \\
&\qquad \mathbf{Q} \in \mathcal{RH}_{\infty} \bigg\}
\end{aligned}
$$
\end{corollary}
\begin{proof}
The proof directly follows by choosing the following doubly-coprime factorization:
\begin{equation} \label{eq:YoulaCo_state}
\begin{aligned}
\mathbf{U}_l &= I, \mathbf{V}_l = -A, \mathbf{N}_l = \frac{1}{z}I, \mathbf{M}_l = I - \frac{1}{z}A,\\
\mathbf{U}_r &= I, \mathbf{V}_r = -A, \mathbf{N}_r = \frac{1}{z}I, \mathbf{M}_r = I - \frac{1}{z}A.\\
\end{aligned}
\end{equation}
\end{proof}
\subsection{Example 1 in~\cite{wang2019system, anderson2019system}}
Consider the following optimal control problem, which is Example 1 in~\cite{wang2019system, anderson2019system},
\begin{equation} \label{eq:Example1}
\begin{aligned}
\min_{\mathbf{K}} \quad &\lim_{T \rightarrow \infty}\frac{1}{T}\sum_{t=0}^T \mathbb{E}||x[t]||_2^2\\
\text{subject to}\quad &~x[t+1]=Ax[t]+u[t]+w[t],\\
\quad &~\mathbf{u}=\mathbf{K}\mathbf{x},
\end{aligned}
\end{equation}
where disturbance $w[t] \stackrel{\text{i.i.d}}{\sim} \mathcal{N}(0,I)$. It can be verified (\emph{e.g.}, via solving the discrete-time algebraic Riccati equation) that the globally optimal solution is the static feedback given by $ \mathbf{K}= -A$.
Assume that $A$ is sparse and let its supports define the adjacency matrix of a graph $\mathcal{G}$. Then, the optimal controller has a particular structure according to $\mathcal{G}$.
Now suppose that we attempt to solve problem~\eqref{eq:Example1} by converting it to
its equivalent $\mathcal{H}_2$ optimal control problem in the form of~\eqref{eq:OCPsparsity}, where the constraint $\mathcal{L}$ corresponds to the sparsity pattern of $A$ (see the Example 1 in~\cite{wang2019system, anderson2019system} for a precise definition). Since~\eqref{eq:OCPsparsity} is not convex in its present form, a certain reformulation is required for numerical computation, \emph{e.g.}, using Youla parameterization, SLP, or IOP.
\begin{proposition}
If the graph $\mathcal{G}$ is strongly connected, then Problem~\eqref{eq:Example1} with a sparsity constraint $\mathbf{K} \in \mathcal{L}$ in the form of~\eqref{eq:OCPsparsity} does not admit any equivalent convex reformulation in Youla, or SLP, or IOP.
\end{proposition}
\begin{proof}
If $\mathcal{G}$ is strongly connected, then the sparsity constraint $\mathcal{L}$ is not QI under $\mathbf{P}_{22} = (zI - A)^{-1}$, since $\mathbf{P}_{22}$ is a dense transfer matrix and it fails to satisfy $\mathbf{K}\mathbf{P}_{22}\mathbf{K} \in \mathcal{L}, \forall \mathbf{K} \in\mathcal{L}$. According to~\cite{lessard2015convexity}, QI is necessary for the existence of an \emph{equivalent} convex reformulation in Youla parameter $\mathbf{Q}$ for~\eqref{eq:OCPsparsity}. The equivalence in Theorem~\ref{theo:equivalence} prevents any \emph{equivalent} convex reformulation via SLP or IOP as well.
\end{proof}
Although there is no equivalent convex reformulation when $\mathcal{G}$ is strongly connected, we could still develop a certain \emph{convex approximation} of~\eqref{eq:OCPsparsity} in Youla parameterization, SLP, or IOP. In the following, we use $\mathcal{I}$ to denote a diagonal structure.
\begin{enumerate}
\item \emph{SLP:}
As suggested by~\cite{wang2019system}, we can add the constraints
$
\mathbf{M} \in \mathcal{L}, \mathbf{R} \in \mathcal{I}
$
to Problem~\eqref{eq:OCPsls}, leading to a convex approximation of~\eqref{eq:OCPsparsity}. It can be checked that $\mathbf{R}= \frac{1}{z}I$ and $\mathbf{M}= -\frac{1}{z}A$ is the optimal solution, recovering the globally optimal controller $\mathbf{K} = \mathbf{M}\mathbf{R}^{-1} = -A$.
\item \emph{Youla parameterization:} We use the simplified Youla parameterization in Corollary~\ref{Corollary:YoulaState}, and add the following constraints
$
-A - (I- \frac{1}{z}A)\textbf{Q} \in \mathcal{L}, I - \frac{1}{z}\textbf{Q} \in \mathcal{I},
$
to Problem~\eqref{eq:OCPYoula}. This leads to a convex program. We can check that the optimal solution is $\textbf{Q} = 0$, leading to
$$
\textbf{K} = \left(-A - (I- \frac{1}{z}A)\textbf{Q}\right)\left(I - \frac{1}{z}\textbf{Q}\right)^{-1} = -A.
$$
\item \emph{IOP:} Since $C_2 = I, B_2 = I$ is invertible, we can use the result in Corollary~\ref{coro:iopstate}. Then, we introduce constraints
$
\mathbf{Z} - I \in \mathcal{L}, \mathbf{W} \in \mathcal{I}
$ to Problem~\eqref{eq:OCPiop}, leading to a convex program. We can check that the solution $\textbf{W} = \frac{1}{z}I$ and $\textbf{Z} = I - \frac{1}{z}A$ is optimal. Then,
$
\textbf{K} = (\textbf{Z}- I)\textbf{W}^{-1} = -A.
$
\end{enumerate}
\begin{remark}[Sparsity invariance and beyond QI]
In the procedures above, we choose separate subspace constraints for the factors of $\mathbf{K}$ in the following form
\begin{equation} \label{eq:SI}
\mathbf{S} \in \mathcal{L}, \mathbf{T} \in \mathcal{I} \quad \Rightarrow \quad \mathbf{K} = \mathbf{S}\mathbf{T}^{-1} \in \mathcal{L},
\end{equation}
where $\mathbf{S}, \mathbf{T}$ denote appropriate transfer matrices in Youla, system-level, and input-output parameterizations. Obviously, this choice leads to a convex inner-approximation of~\eqref{eq:OCPsparsity} since the feasible region of $\mathbf{K}$ is narrowed. For this simple instance, the globally optimal solution is parameterized when using~\eqref{eq:SI}. Thus, the globally optimal controller can be found using Youla, system-level or input-output parameters via convex optimization. However, as observed in~\cite{Furieri2019Sparsity}, this procedure has no guarantee of optimility for general constraints beyond QI using either of Youa parameterization, SLP or IOP.
We note that the property~\eqref{eq:SI} is a special case of sparsity invariance (SI)~\cite{Furieri2019Sparsity}. There may exist other subspace choices for $\mathbf{S}, \mathbf{T}$ satisfying $\mathbf{S}\mathbf{T}^{-1} \in \mathcal{L}$, which still return a structured controller $\mathbf{K} \in \mathcal{L}$. Indeed, the notion of SI goes beyond QI for sparsity constraints, as it includes QI as a special case. We refer the interested reader to~\cite{Furieri2019Sparsity} for details.
\end{remark}
\section{Conclusion} \label{section:conclusion}
In this paper, we have presented an explicit equivalence of Youla, system-level, and input-output parameterizations for the set of internally stabilizing controllers. A doubly-coprime factorization of the system can be considered as a way to eliminate the explicit equality constraints in SLP and IOP. Indeed, both SLP and IOP have four parameters; but due to the equality constraints, SLP and IOP have the same degree of freedom as Youla parameterization.
We remark that the equivalence of Youla, SLP, and IOP does not indicate they offer the same computational features. One parameterization may be better suited for a particular context. For instance, it seems that SLP is more convenient for the case of state feedback, which has found applications in quantifying sample complexity of LQR problems~\cite{dean2017sample}; IOP seems to better suit for the case of output feedback as it exclusively deals with the maps from inputs to outputs without explicitly touching the system state; and Youla parameterization is more convenient when a doubly-coprime factorization is available \emph{a priori}. It is interesting to investigate whether there exist other parameterizations of stabilizing controllers that suit for a particular control application. Finally, we note that Youla, SLP, and IOP naturally suit for parameterizing dynamical controllers, but none of them can parameterize the set of static stabilizing controllers in a convex way. Thus, QI is not relevant for structured static controller synthesis, and this problem deserves further investigations.
\appendix
\subsection{Proof of Statement 2 in Theorem~\ref{th:slp_eq}} \label{Sec:stable}
Given any $\mathbf{Y}, \mathbf{U}, \mathbf{W}, \mathbf{Z}$ satisfying the affine subspace~\eqref{eq:aff1}-\eqref{eq:aff3}, we know that $\mathbf{K} = \mathbf{U}\mathbf{Y}^{-1}$ internally stabilizes the plant $\mathbf{P}_{22}$. In the following, we verify that the transfer matrices $\mathbf{R},\mathbf{M},\mathbf{N},\mathbf{L}$ defined in~\eqref{eq:iop-sls} are exactly the closed-loop responses in~\eqref{eq:LTIsls} with controller $\mathbf{K} = \mathbf{U}\mathbf{Y}^{-1}$.
Recall that $\mathbf{P}_{22}$ is strictly proper, \emph{i.e.}, $\mathbf{P}_{22} = C_2(zI - A)^{-1}B_2$. Then, we can verify the following equation:
$$
\begin{aligned}
\mathbf{R} &= (zI - A)^{-1} + (zI - A)^{-1}B_2\mathbf{U}C_2(zI - A)^{-1} \\
&=\left[(I + B_2\mathbf{U}C_2(zI - A)^{-1})^{-1}(zI - A)\right]^{-1}
\\
&= \left[ zI - A - (I + B_2\mathbf{U}C_2(zI - A)^{-1})^{-1}B_2\mathbf{U}C_2\right]^{-1}\\
&= \left[ zI - A - B_2\mathbf{U}(I + C_2(zI - A)^{-1}B_2\mathbf{U})^{-1}C_2\right]^{-1} \\
&= \left(zI - A - B_2\mathbf{U}\mathbf{Y}^{-1}C_2\right)^{-1}\\
&= (zI - A - B_2\mathbf{K}C_2)^{-1}
\end{aligned}
$$
Also, we can verify
$$
\begin{aligned}
\mathbf{M} & = \mathbf{U}C_2(zI - A)^{-1}=(I - \mathbf{K}\mathbf{P}_{22})^{-1}\mathbf{K}C_2(zI - A)^{-1} \\
&=\mathbf{K}C_2(zI - A)^{-1}(I - B_2\mathbf{K}C_2(zI - A)^{-1})^{-1} \\
&=\mathbf{K}C_2(zI-A - B_2\mathbf{K}C_2)^{-1} \\
&=\mathbf{K}C_2\mathbf{R}
\end{aligned}
$$
Similarly, we have
$ \mathbf{N} = (zI - A)^{-1}B_2\mathbf{U} = \mathbf{R}B_2\mathbf{K}
\nonumber,
\mathbf{L} = \mathbf{U} = \mathbf{K}(I - \mathbf{P}_{22}\mathbf{K})^{-1}. $
Then, the transfer matrices $\mathbf{R},\mathbf{M},\mathbf{N},\mathbf{L}$ are exactly the closed-loop responses in~\eqref{eq:LTIsls} with $\mathbf{K} = \mathbf{U}\mathbf{Y}^{-1}$.
\subsection{Proof of~\eqref{eq:slp-stable-state}} \label{section:proofB}
We show that any controller in~\eqref{eq:slp-stable-state} is an internally stabilizing controller in~\eqref{eq:sls}. The other direction is similar.
Consider any $\mathbf{R}, \mathbf{M}\in \frac{1}{z}\mathcal{RH}_{\infty}$ satisfying
$$ \begin{bmatrix} (zI -A) & -B_2 \end{bmatrix} \begin{bmatrix} \mathbf{R} \\ \mathbf{M} \end{bmatrix} = I.
$$
Upon defining $ \mathbf{L} = \mathbf{M}(zI - A),
\mathbf{N}=\mathbf{R}(zI - A) - I,
$
it is easy to see $ \mathbf{N}, \mathbf{L} \in \mathcal{RH}_{\infty}$. Also, one can straightforwardly verify that $\mathbf{N}, \mathbf{L}$ and $\mathbf{R}, \mathbf{M}$ above satisfy~\eqref{eq:slp_s1}-\eqref{eq:slp_s2} when $C_2 = I$. It is routinely to verify that
$
\textbf{L} - \textbf{M}\textbf{R}^{-1}\textbf{N} = \textbf{M}(sI - A) - \textbf{M}\textbf{R}^{-1}(\textbf{R}(sI - A) - I)
= \textbf{M}\textbf{R}^{-1}.
$
It remains to check that $\mathbf{N}$ defined above is strictly proper. This fact follows from~\eqref{eq:slp_s2} that
$
\mathbf{N} = (zI - A)^{-1}B_2 \mathbf{L},
$
indicating that~\eqref{eq:slp_s3} also hold. Thus, the general parameterization~\eqref{eq:sls} can be reduced to~\eqref{eq:slp-stable-state}.
\subsection{Stable plants} \label{section:special}
When $\mathbf{P}_{22} \in \mathcal{RH}_{\infty}$, we show that Youla, SLP, and IOP can be simplified, and only two paramters are required in SLP/IOP.
\begin{proposition} \label{prop:stable}
If $\mathbf{P}_{22} \in \mathcal{RH}_{\infty}$, we have:
\begin{enumerate}
\item Youla parameterization can be reduced to
\begin{equation} \label{eq:youla-stable}
\mathcal{C}_{\text{stab}} = \{\mathbf{K} = - \mathbf{Q}(I - \mathbf{P}_{22}\mathbf{Q})^{-1} \mid \mathbf{Q} \in \mathcal{RH}_{\infty} \}.
\end{equation}
\item For strictly proper $\mathbf{P}_{22}$, SLP can be reduced to
\begin{equation} \label{eq:slp-stable}
\begin{aligned}
\mathcal{C}_{\text{stab}} = \bigg\{\mathbf{K} = &\mathbf{L}(C_2\mathbf{N} + I)^{-1} \bigm| \mathbf{L} \in \mathcal{RH}_{\infty}, \\
&\begin{bmatrix} (zI -A) & -B_2 \end{bmatrix} \begin{bmatrix} \mathbf{N} \\ \mathbf{L} \end{bmatrix} = 0
\bigg \}.
\end{aligned}
\end{equation}
\item IOP can be reduced to
\begin{equation} \label{eq:iop-stable}
\begin{aligned}
\mathcal{C}_{\text{stab}} = \bigg\{\mathbf{K} = \mathbf{U}\mathbf{Y}^{-1} \bigm| \begin{bmatrix} I & -\mathbf{P}_{22} \end{bmatrix} \begin{bmatrix} \mathbf{Y} \\ \mathbf{U} \end{bmatrix} = I, \\
\mathbf{U} \in \mathcal{RH}_{\infty}
\bigg\}.
\end{aligned}
\end{equation}
\end{enumerate}
\end{proposition}
\emph{Proof:} The proof is directly from the following observations.
\begin{enumerate}
\item If $\mathbf{P}_{22} \in \mathcal{RH}_{\infty}$, a doubly-coprime factorization of $\mathbf{P}_{22}$ can be trivially chosen as $
\mathbf{U}_l = I, \mathbf{V}_l = 0, \mathbf{N}_l = \mathbf{P}_{22}, \mathbf{M}_l = I,
\mathbf{U}_r = I, \mathbf{V}_r = 0, \mathbf{N}_r = \mathbf{P}_{22}, \mathbf{M}_r = I.
$
Then, the parameterization~\eqref{eq:youla} is reduced to~\eqref{eq:youla-stable}.
\item Given $\mathbf{N}, \mathbf{L}$ in~\eqref{eq:slp-stable}, we define
$
\mathbf{R} = (zI -A)^{-1} + \mathbf{N}C_2(zI - A)^{-1},
\mathbf{M} = \mathbf{L}C_2(zI - A)^{-1}.
$
Considering $(zI - A)^{-1} \in \mathcal{RH}_{\infty}$, if $\mathbf{L} \in \mathcal{RH}_{\infty}$, we have $ \mathbf{N}, \mathbf{R}, \mathbf{M} \in \frac{1}{z}\mathcal{RH}_{\infty}$. It can be verified that the $\mathbf{R}, \mathbf{M}, \mathbf{N}, \mathbf{L}$ above satisfies~\eqref{eq:slp_s1}-\eqref{eq:slp_s3} when~\eqref{eq:slp-stable} holds. Also, we have
$$
\begin{aligned}
\mathbf{L} - \mathbf{M}\mathbf{R}^{-1}\mathbf{N}
& = \mathbf{L} -\mathbf{L}C_2(I + \mathbf{N}C_2)^{-1}\mathbf{N} \\
& = \mathbf{L}(C_2\mathbf{N} + I)^{-1}.
\end{aligned}
$$
Thus,~\eqref{eq:slp_s1}-\eqref{eq:slp_s3} can be reduced to~\eqref{eq:slp-stable}.
\item Upon defining
$
\mathbf{Y} = I + \mathbf{P}_{22}\mathbf{U},
\mathbf{Z} = I + \mathbf{U}\mathbf{P}_{22},
\mathbf{W} = \mathbf{P}_{22} \mathbf{Z},
$
we have $\mathbf{Y}, \mathbf{W}, \mathbf{Z} \in \mathcal{RH}_{\infty}$
if $\mathbf{P}_{22}, \mathbf{U} \in \mathcal{RH}_{\infty}$. Also, the $\mathbf{Y}, \mathbf{U}, \mathbf{W}, \mathbf{Z}$ above satisfies~\eqref{eq:aff1}-\eqref{eq:aff2} if~\eqref{eq:iop-stable} holds. Thus,~\eqref{eq:aff1}-\eqref{eq:aff3} can be reduced to~\eqref{eq:iop-stable}.
\end{enumerate}
\begin{remark}\label{remark:stableQ}
The first statement in Proposition~\ref{prop:stable} is a classical result~\cite[Corollary 5.5]{zhou1996robust}. We note that parameterizations~\eqref{eq:slp-stable} and~\eqref{eq:iop-stable} are identical to~\eqref{eq:youla-stable} by noticing that
$
\mathbf{L} = \mathbf{U} = - \mathbf{Q}.
$ They are all reduced to the same form.
\end{remark}
\end{document} | math |
\betagin{document}
\baselineskip 18pt
\hfuzz=6pt
\newtheorem{theorem}{Theorem}[section]
\newtheorem{prop}[theorem]{Proposition}
\newtheorem{lemma}[theorem]{Lemma}
\newtheorem{definition}[theorem]{Definition}
\newtheorem{cor}[theorem]{Corollary}
\newtheorem{example}[theorem]{Example}
\newtheorem{remark}[theorem]{Remark}
\newcommand{\rightarrow}{\rightarrow}
\renewcommand{\theequation}
{\thesection.\arabic{equation}}
\newcommand{{\mathcal C}}{{\mathcal C}}
\newcommand{1\hspace{-4.5pt}1}{1\hspace{-4.5pt}1}
\newcommand{\widehat}{\widehat}
\newcommand{\frac}{\fracrac}
\newcommand{\dfrac}{\dfracrac}
\newcommand{\textup{sgn\,}}{\textup{sgn\,}}
\newcommand{\mathbb R^n}{\mathbb R^n}
\newcommand{\sigma}{\sigmagma}
\newcommand{\gamma}{\gammamma}
\newcommand{\infty}{\infty}
\newcommand{\partial}{\partialartial}
\newcommand{\Delta}{\Deltalta}
\newcommand{\norm}[1]{\left\|{#1}\right\|}
\newcommand{\operatorname{supp}}{\operatorname{supp}}
\newcommand{\tfrac}{\tfracrac}
\newcommand{\quad\quad}{\quad\quad}
\newcommand{\label}{\labelel}
\newcommand{\mathbf Z}{\mathbf Z}
\newcommand{L^{\infty}}{L^{\infty}}
\newcommand{\int_{\rn}}{\int_{\mathbb R^n}}
\newcommand{\quad\quadq}{\quad\quad\quad}
\newcommand{\varphi}{\varphi}
\newcommand{\alpha}{\alphapha}
\newcommand{\mathbb R}{\mathbb RR}
\newcommand{\int_{\R}}{\int_{\mathbb R}}
\newcommand{\int_{\R}r}{\int_{\mathbb R^2}}
\newcommand{\delta}{\deltalta}
\newcommand{\omega}{\omegaega}
\newcommand{\Theta}{\Theta}
\newcommand{\theta}{\theta}
\newcounter{question}
\newcommand{\qt}{
\stepcounter{question}
\thequestion}
\newcommand{\fbox{Q\qt}\ }{\fracbox{Q\qt}\ }
\renewcommand{\Psi}{\Psi}
\newcommand{\si_{gg}}{\sigma_{gg}}
\newcommand{\si_{b2j}}{\sigma_{b2j}}
\newcommand{\si_{b3k}}{\sigma_{b3k}}
\newcommand{\si_{b_0g}}{\sigma_{b_0g}}
\newcommand{\abs}[1]{\left\varepsilonrt #1\right\varepsilonrt}
\newcommand{\beta}{\betata}
\deltaf\mathbb RR{\mathbb R}
\deltaf\mathbb R{\mathbb R}
\deltaf\mathbb N{\mathbb N}
\deltaf\mathbb Rn{\mathbb R^n}
\deltaf\mathbb Z{\mathbb Z}
\deltaf\varepsilon{\varepsilon}
\title[A sharp version of the H\"ormander Multiplier Theorem]
{A sharp version of the H\"ormander Multiplier Theorem}
\thanks{ }
\author{Loukas Grafakos}
\address{Department of Mathematics, University of Missouri, Columbia MO 65211, USA}
\email{grafakosl@missouri.edu}
\author{Lenka Slav\'ikov\'a}
\address{Department of Mathematics, University of Missouri, Columbia MO 65211, USA}
\email{slavikoval@missouri.edu}
\thanks{{\it Mathematics Subject Classification:} Primary 42B15. Secondary 42B25}
\thanks{The first author acknowledges the support of the Simons Foundation and of the University of Missouri Research Board.}
\betagin{abstract}
We provide an improvement of the H\"ormander multiplier theorem in which the Sobolev space $L^r_s(\mathbb R^n)$ with
integrability index $r$ and smoothness index $s>n/r$ is replaced by the Sobolev space with smoothness $s$ built upon the Lorentz space $L^{n/s,1}(\mathbb R^n)$.
\end{abstract}
\maketitle
\section{Introduction}
Given a bounded function $\sigma$ on $\mathbb R^n$, we define a linear operator
$$
T_\sigma(f)(x) = \int_{\mathbb R^n} \widehat{f}(\xi) \sigma(\xi) e^{2\partiali i x\cdot \xi}d\xi
$$
acting on Schwartz functions $f$ on $\mathbb R^n$; here
$\widehat{f}(\xi) = \int_{\mathbb R^n} f(x) e^{-2\partiali i x\cdot \xi}dx$ is the Fourier transform of $f$.
An old problem in harmonic analysis is to find optimal sufficient conditions on $\sigma$ to be
an $L^p$ Fourier multiplier, i.e., for the
operator $T_\sigma$ to admit a bounded extension from $L^p(\mathbb R^n)$ to itself for a given $p\in (1,\infty)$.
Mikhlin's~\cite{Mikhlin} classical multiplier theorem states that if the condition
\betagin{equation}\labelel{10}
|\partialartial^\alphapha \sigma(\xi)|\leq C_\alphapha |\xi|^{-| \alphapha|}, \quad\quaduad \xi\neq 0,
\end{equation}
holds for all { multi-indices} $\alpha$ with size $|\alpha | \le [n/2]+1$, then $T_\sigma$ admits a bounded extension from
$L^p(\mathbb R^n)$ to itself for all $1<p<\infty$. This theorem is well suited for dealing with multipliers whose derivatives have a singularity at one point, such as functions which are homogeneous of degree zero and indefinitely differentiable on the unit sphere.
An extension of the Mikhlin theorem was obtained by H\"ormander~\cite{Hoe}. It asserts the following: for $s>0$ let $(I-\Delta)^{s/2} $ denote the operator given on the Fourier transform by multiplication by
$(1+4\partiali^2 |\xi|^2)^{s/2}$ and let $\Psi$ be a Schwartz function whose Fourier transform is supported in the annulus
$\{\xi: 1/2< |\xi|< 2\}$ and which satisfies $\sum_{j\in \mathbb Z} \widehat{\Psi}(2^{-j}\xi)=1$ for all $\xi\neq 0$. If for some $1\le r\le 2$ and $s>n/r$, $\sigma$ satisfies
\betagin{equation}\labelel{2}
\sup_{k\in \mathbb Z} \big\|(I-\Delta)^{s/2} \big[ \widehat{\Psi}\sigma (2^k \cdot)\big] \big\|_{L^r(\mathbb R^n) }<\infty,
\end{equation}
then $T_\sigma$ admits a bounded extension from
$L^p(\mathbb R^n)$ to itself for all $1<p<\infty$.
It is natural to ask whether condition~\eqref{2} can still guarantee that $\sigmagma$ is an $L^p$ Fourier multiplier for some $p\in (1,\infty)$ if $s\leq \fracrac{n}{2}$.
Via an interpolation argument,
Calder\'on and Torchinsky~\cite[Theorem 4.6]{CT} showed that $T_\sigma$ is bounded from $L^p(\mathbb R^n)$ to itself whenever condition~\eqref{2} holds with $p$ satisfying
$\big| \frac 1p -\frac 12 \big| <\frac sn$ and $\big| \frac 1p -\frac 12 \big| = \frac 1r $. It was observed in \cite{GraHeHonNg1} that the assumption $\big| \frac 1p -\frac 12 \big| = \frac 1r $ can be replaced by a weaker one, namely, by $\fracrac{1}{r}<\fracrac{s}{n}$. Moreover, it is known that if
$T_\sigma$ is bounded from $L^p(\mathbb R^n)$ to itself for every $\sigmagma$ satisfying~\eqref{2}, then $\big| \frac 1p -\frac 12 \big| \le \frac sn$, see Hirschman~\cite{hirschman2}, Wainger~\cite{W}, Miyachi~\cite{Miy}, Miyachi and Tomita~\cite{MT}, Grafakos, He, Honz\'\i k, and Nguyen~\cite{GraHeHonNg1}.
In other words, when $rs>n$, then the condition $\big| \frac 1p -\frac 12 \big| <\frac sn$ is essentially optimal for assumption \eqref{2}.
Observe also that the condition $rs>n$ is dictated by the embedding of $L^r_s(\mathbb R^n) \hookrightarrow L^\infty(\mathbb R^n)$.
It is still unknown to us if $L^p$ boundedness holds on the line $\big| \frac 1p -\frac 12 \big| =\frac sn$ although other positive results on this line for $1<p<2$ and on $H^1$ can be found in Seeger~\cite{Seeger1}, ~\cite{Seeger2}.
\betagin{comment} Unlike the Mikhlin multiplier theorem, the previous two theorems can be applied to prove boundedness of multipliers $\sigmagma$ whose derivatives have singularities at infinitely many points. An important example of this are multipliers whose derivatives have singularities on the sphere, such as the Bochner-Riesz operators corresponding to $\sigmagma(x)=(1-|x|^2)_+^{\deltalta}$. It is known, however, that the sufficient conditions obtained in this way are not the optimal ones.
\end{comment}
Unlike the Mikhlin multiplier theorem, the H\"ormander and Calder\'on-Torchinsky theorems can treat multipliers whose derivatives have infinitely many singularities, such as the multiplier
\betagin{equation}\labelel{E:power_type}
\sigmagma(x)=\sum_{k\in \mathbb Z} \partialhi(2^{-k}x) |2^{-k}x-a_k|^\betata,
\end{equation}
where $\betata<0$, $\partialhi$ is a smooth function supported in the set $\{x\in \mathbb R^n: \fracrac{1}{2}<|x|<2\}$ and, for every $k\in \mathbb N$, $a_k\in \mathbb R^n$ belongs to
the same set.
In this paper, we improve the result of~\cite[Theorem 4.6]{CT} by replacing the Lebesgue space $L^r(\mathbb R^n)$, $r>\fracrac{n}{s}$, in condition~\eqref{2} by the locally larger Lorentz space $L^{\fracrac{n}{s},1}(\mathbb R^n)$, defined in terms of the norm
$$
\|f\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}=\int_0^\infty f^*(r)r^{\fracrac{s}{n}-1}\,dr.
$$
Here, $f^*$ stands for the nonincreasing rearrangement of the function $f$, namely, for the unique nonincreasing left-continuous function on $(0,\infty)$ equimeasurable with $f$, given by the explicit expression
$$
f^*(t)= \inf \big\{r\ge 0:\,\, |\{y\in \mathbb R^n:\,\, |f(y)|>r\}| < t \big\}\, .
$$
We point out that the Lorentz space $L^{\fracrac{n}{s},1}(\mathbb R^n)$ appears naturally in this context, since it is known to be, at least for integer values of $s$, locally the largest rearrangement-invariant function space such that membership of $(I-\Deltalta)^\fracrac{s}{2}f$ to this space forces
$f$ to be bounded, see~\cite{S, CP}.
\betagin{comment}
[note: this is known at least for derivatives of integer order; I am not sure about fractional derivatives, but I expect it to be true as well]
\end{comment}
\betagin{theorem}\labelel{T:main_theorem}
Let $\Psi$ be a Schwartz function on $\mathbb R^n$ whose Fourier transform is supported in the annulus $1/2<|\xi|<2$
and satisfies $\sum_{j\in \mathbb Z} \widehat{\Psi} ( 2^{-j} \xi) =1$, $\xi\neq 0$.
Let $p\in (1,\infty)$, $n\in \mathbb N$, and let $s\in (0,n)$ satisfy
$$
\left|\fracrac{1}{p}-\fracrac{1}{2}\right|<\fracrac{s}{n}.
$$
Then for all functions $f$ in the Schwartz class of $\mathbb R^n$ we have the a priori estimate
\betagin{equation}\labelel{E:inequality}
\|T_\sigmagma f\|_{L^p(\mathbb Rn)} \leq C \sup_{j\in \mathbb Z} \big\|(I-\Deltalta)^{\fracrac{s}{2}}[\widehat\Psi \sigma(2^j\cdot)\big]\big\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)} \|f\|_{L^p(\mathbb Rn)}.
\end{equation}
\end{theorem}
As an application of Theorem~\ref{T:main_theorem} we show that the function $\sigmagma$ from~\eqref{E:power_type} continues to be an $L^p$ Fourier multiplier for any $p\in (1,\infty)$ if $|2^{-k}x-a_k|$ is replaced by $\log \fracrac{e4^n}{|2^{-k}x-a_k|^n}$. In fact, we can even allow an arbitrary iteration of logarithms in this example.
\betagin{example}\labelel{E:example}
Assume that $n\in \mathbb N$, $n\geq 2$, and $\betata<0$.
Let $\partialhi$ be a smooth function supported in the set $A = \{x\in \mathbb R^n: 1/2<|x|<2\}$ and let $a_k\in A$, $k\in \mathbb Z$. Then the function
\betagin{equation}\labelel{E:logarithmic_type}
\sigmagma(x)=\sum_{k\in \mathbb Z} \partialhi(2^{-k}x) \left(\log \fracrac{e4^n}{|2^{-k}x-a_k|^n}\right)^\betata
\end{equation}
is an $L^p$ Fourier multiplier for any $p\in (1,\infty)$.
\end{example}
To verify the statement of Example~\ref{E:example}, we fix a positive integer $s$ and observe that for any $j\in \mathbb Z$,
\betagin{align*}
&\|(I-\Deltalta)^{\fracrac{s}{2}}[\widehat{\Psi}\sigmagma(2^j\cdot)]\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}
\leq \left\|(I-\Deltalta)^{\fracrac{s}{2}}\left[\widehat{\Psi}(x) \partialhi(x) \left(\log \fracrac{e4^n}{|x-a_j|^n}\right)^\betata\right]\right\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}\\
&\quad\quaduad\quad\quaduad\quad\quaduad\quad\quaduad+\left\|(I-\Deltalta)^{\fracrac{s}{2}}\left[\widehat{\Psi}(x) \partialhi(2x) \left(\log \fracrac{e4^n}{|2x-a_{j-1}|^n}\right)^\betata\right]\right\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}\\
&\quad\quaduad\quad\quaduad\quad\quaduad\quad\quaduad+\left\|(I-\Deltalta)^{\fracrac{s}{2}}\left[\widehat{\Psi}(x) \partialhi\big(\fracrac{x}{2}\big) \left(\log \fracrac{e4^n}{|\fracrac{x}{2}-a_{j+1}|^n}\right)^\betata\right]\right\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)} .
\end{align*}
In what follows, let us deal with the first term only, since the latter two terms can be estimated in a similar way.
Fix $j\in \mathbb Z$ and denote
$$
f_j(x)=\widehat{\Psi}(x) \partialhi(x) \left(\log \fracrac{e4^n}{|x-a_j|^n}\right)^\betata.
$$
Also, for any multiindex $\alphapha$ satisfying $|\alphapha|\geq 1$, let $\fracrac{\partialartial^\alphapha}{\partialartial x^\alphapha} f_j$ stand for the weak derivative of $f_j$ with respect to $\alphapha$.
We have
$$
\left|\fracrac{\partialartial^\alphapha}{\partialartial x^\alphapha} f_j(x)\right| \leq C \chi_A(x) \left(\log \fracrac{e4^n}{|x-a_j|^{n}}\right)^{\betata-1} |x-a_j|^{-|\alphapha|}.
$$
Since $|A|\leq 2^n \omegaega_n$, where $\omegaega_n$ stands for the volume of the unit ball in $\mathbb R^n$, the previous estimate implies
$$
\left(\fracrac{\partialartial^\alphapha}{\partialartial x^\alphapha} f_j\right)^*(t)\leq C \chi_{(0,2^n \omegaega_n)}(t) \left(\log \fracrac{e4^n \omegaega_n}{t}\right)^{\betata-1} t^{-\fracrac{|\alphapha|}{n}},
$$
where the constant $C$ is independent of $j$.
Therefore, if $s$ is a positive integer and $\alphapha$ is a multiindex with $1\leq |\alphapha|\leq s$, then
$$
\left(\fracrac{\partialartial^\alphapha}{\partialartial x^\alphapha} f_j\right)^*(t)\leq C \chi_{(0,2^n \omegaega_n)}(t) \left(\log \fracrac{e4^n \omegaega_n}{t}\right)^{\betata-1} t^{-\fracrac{s}{n}}.
$$
Consequently,
\betagin{equation}\labelel{E:sobolev}
\sup_{1\leq |\alphapha|\leq s} \left\|\fracrac{\partialartial^\alphapha}{\partialartial x^\alphapha} f_j\right\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}
\leq C \int_0^{2^n \omegaega_n} \left(\log \fracrac{e4^n \omegaega_n}{t}\right)^{\betata-1} t^{-1}\,dt<\infty.
\end{equation}
Since each $|f_j|$ is bounded by a constant independent of $j$ and compactly supported in the set $A$, we also have
$$
\|f_j\|_{L^{\fracrac{n}{s}}(\mathbb R^n)}\leq C<\infty.
$$
It remains to observe that the quantity $\|(I-\Deltalta)^{\fracrac{s}{2}}f_j\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}$
is equivalent to
$$
\sum_{|\alphapha|\leq s} \left\|\fracrac{\partialartial^\alphapha}{\partialartial x^\alphapha} f_j\right\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}.
$$
This can be proved in exactly the same way as the corresponding result for the Lebesgue spaces, see, e.g., \cite[Theorem 3, Chapter 5]{St1}. Therefore, we deduce that
$$
\sup_{j\in \mathbb Z} \|(I-\Deltalta)^{\fracrac{s}{2}}[\widehat{\Psi}\sigmagma(2^j\cdot)]\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}<\infty
$$
for any positive integer $s$. Theorem~\ref{T:main_theorem} now yields that $\sigmagma$ is an $L^p$ Fourier multiplier for any $p\in (1,\infty)$.
Finally, notice that we can in fact replace the logarithm in~\eqref{E:logarithmic_type} by any iteration of logarithms, namely, we can consider the more general symbol
\betagin{equation*}
\sigmagma(x)=\sum_{k\in \mathbb Z} \partialhi(2^{-k}x) \left(\underbrace{\log \cdots \log}_{\ell-\textup{times}} \fracrac{4^n\underbrace{e^{.{^{.{^{.{e}}}}}}}_{\ell- \textup{times}}}{|2^{-k}x-a_k|^n}\right)^\betata,
\end{equation*}
where $\ell$ is any positive integer.
A computation similar to the one we performed above shows that $\sigmagma$ is an $L^p$ Fourier multiplier for any $p\in (1,\infty)$ as well.
\section{The main estimate}
In this section we show that inequality~\eqref{E:inequality} holds for any $p\in (1,\infty)$ provided that $s\in (n/2,n)$, see Theorem~\ref{T:endpoint} below. This estimate will serve as one endpoint in the interpolation argument leading to the proof of Theorem~\ref{T:main_theorem}. The interpolation is the content of the next section.
Let us start by recalling the definitions of two types of Lorentz spaces that will be used in the sequel. Suppose that $1<p<\infty$. Then, for any measurable function $f$ on $\mathbb R^n$, we define
$$
\|f\|_{L^{p,1}(\mathbb R^n)}=\int_0^\infty f^*(t) t^{\fracrac{1}{p}-1}\,dt
$$
and
$$
\|f\|_{L^{p,\infty}(\mathbb R^n)}=\sup_{t>0} f^*(t) t^{\fracrac{1}{p}}.
$$
It can be shown that
$$
\|f\|_{L^{p,1}(\mathbb R^n)}=p\int_0^\infty |\{x\in \mathbb R^n: |f(x)|>\lambda\}|^{\fracrac{1}{p}}\,d\lambda
$$
and
$$
\|f\|_{L^{p,\infty}(\mathbb R^n)}=\sup_{\lambda>0} \lambda |\{x\in \mathbb R^n: |f(x)|>\lambda\}|^{\fracrac{1}{p}}.
$$
The space $L^{p',\infty}(\mathbb R^n)$, where $p'=\fracrac{p}{p-1}$, is a kind of a measure theoretic dual of the space $L^{p,1}(\mathbb R^n)$, in the sense that the following form of H\"older's inequality
$$
\int_{\mathbb R^n} |fg| \leq \|f\|_{L^{p,1}(\mathbb R^n)} \|g\|_{L^{p',\infty}(\mathbb R^n)}
$$
holds.
In what follows, $B(x,r)$ denotes the ball centered at point $x$ and having the radius $r$. If a ball of radius $r$ is centered at the origin, we shall denote it simply by $B_r$.
Let $q\geq 1$ be a real number. We consider the centered maximal operator $M_{L^q}$ defined by
$$
M_{L^q} f(x) = \sup_{r>0} \left(\fracrac{1}{|B(x,r)|} \int_{B(x,r)} |f(y)|^q\,dy\right)^{\fracrac{1}{q}}.
$$
Observe that
$$
M_{L^q} f=(M |f|^q)^{\fracrac{1}{q}},
$$
where $M$ stands for the classical Hardy-Littlewood maximal operator.
The crucial step towards proving Theorem~\ref{T:endpoint} is the following lemma, which can be understood as a sharp variant of ~\cite[Theorem 2.1.10]{CFA}.
\betagin{lemma}\labelel{L:lemma}
Assume that $n\in \mathbb N$, $s \in (0,n)$ and $q>\fracrac{n}{s}$. Then there is a positive constant $C$ depending on $n$, $s$ and $q$ such that for any $j\in \mathbb Z$ and any measurable function $f$ on $\mathbb Rn$,
\betagin{equation}\labelel{E:estimate}
\left\|\fracrac{f(x+2^{-j}y)}{(1+|y|)^{s}}\right\|_{L^{\fracrac{n}{s},\infty}(\mathbb Rn)} \leq C M_{L^q} f(x), \quad x\in \mathbb Rn.
\end{equation}
\end{lemma}
\betagin{proof}
We may assume, without loss of generality, that $j=0$ and $x=0$. Indeed, setting $g(y)=f(x+2^{-j}y)$, we obtain
\betagin{equation}\labelel{E:reduction1}
\left\|\fracrac{f(x+2^{-j}y)}{(1+|y|)^{s}}\right\|_{L^{\fracrac{n}{s},\infty}(\mathbb Rn)} = \left\|\fracrac{g(y)}{(1+|y|)^{s}}\right\|_{L^{\fracrac{n}{s},\infty}(\mathbb Rn)}
\end{equation}
and
\betagin{align}\labelel{E:reduction2}
M_{L^q} f(x)
&=\sup_{r>0} \left(\fracrac{1}{|B(x,r)|} \int_{B(x,r)} |f(y)|^q\,dy\right)^{\fracrac{1}{q}}\\
\nonumber
&=\sup_{r>0} \left(\fracrac{1}{2^{jn}|B(x,r)|} \int_{B(0,2^j r)} |f(x+2^{-j}z)|^q\,dz\right)^{\fracrac{1}{q}}\\
\nonumber
&=\sup_{r'>0} \left(\fracrac{1}{|B(0,r')|} \int_{B(0,r')} |g(y)|^q\,dy\right)^{\fracrac{1}{q}}\\
\nonumber
&=M_{L^q} g(0).
\end{align}
Hence, it suffices to show that for any measurable function $g$ on $\mathbb Rn$,
\betagin{equation}\labelel{E:reduced_inequality}
\left\|\fracrac{g(y)}{(1+|y|)^{s}}\right\|_{L^{\fracrac{n}{s},\infty}(\mathbb Rn)} \leq C M_{L^q} g(0).
\end{equation}
If $M_{L^q} g(0)=\infty$, then inequality~\eqref{E:reduced_inequality} holds trivially, so we can assume in what follows that $M_{L^q} g(0)<\infty$. Since the case $M_{L^q} g(0)=0$ is trivial as well (as $g$ needs to vanish a.e.\ in this case), dividing the function $g$ by the positive constant $M_{L^q} g(0)$, we can in fact assume that $M_{L^q} g(0)=1$.
Fix any $a>0$ and $k\in \mathbb N_0$. Then
\betagin{align*}
|\{y\in B_{2^{k+1}}\setminus B_{2^{k}}: |g(y)|>a\}|
&\leq \fracrac{1}{a^q}\int_{B_{2^{k+1}}\setminus B_{2^{k}}} |g(y)|^q\,dy\\
&\leq \fracrac{|B_{2^{k+1}}| }{a^q}\cdot \fracrac{1}{|B_{2^{k+1}}|} \int_{B_{2^{k+1}}} |g(y)|^q\,dy
\leq \fracrac{\omegaega_n 2^{(k+1)n}}{a^q},
\end{align*}
where $\omegaega_n$ denotes the volume of the unit ball in $\mathbb Rn$. Combining this with the trivial estimate
$$
|\{y\in B_{2^{k+1}}\setminus B_{2^{k}}: |g(y)|>a\}| \leq \omegaega_n 2^{(k+1)n},
$$
we deduce that
\betagin{align*}
&\left|\left\{y\in \mathbb Rn: \fracrac{|g(y)|}{(1+|y|)^s}>a\right\}\right|\\
&=\left|\left\{y\in B_1: \fracrac{|g(y)|}{(1+|y|)^s}>a\right\}\right| +\sum_{k=0}^\infty \left|\left\{y\in B_{2^{k+1}}\setminus B_{2^{k}}: \fracrac{|g(y)|}{(1+|y|)^s}>a\right\}\right|\\
&\leq \left|\left\{y\in B_1: |g(y)|>a\right\}\right| + \sum_{k=0}^\infty \left|\left\{y\in B_{2^{k+1}}\setminus B_{2^k} : |g(y)|> 2^{ks} a\right\}\right|\\
&\leq \left|\left\{y\in B_1: |g(y)|>a\right\}\right| + \sum_{k=0}^\infty \omegaega_n 2^{(k+1)n} \min\left\{\fracrac{1}{2^{ksq} a^q}, 1 \right\}\\
&\leq \left|\left\{y\in B_1: |g(y)|>a\right\}\right| + \sum_{k\in \mathbb N_0: 2^k<\fracrac{1}{a^{ {1}/{s}}}} \omegaega_n 2^n \cdot 2^{kn} + \sum_{k\in \mathbb N_0: 2^k \geq \fracrac{1}{a^{ {1}/{s}}}} \fracrac{\omegaega_n 2^n}{a^q} \cdot 2^{k(n-sq)}\\
&\leq \left|\left\{y\in B_1: |g(y)|>a\right\}\right| + \fracrac{C}{a^{\fracrac{n}{s}}}.
\end{align*}
Notice that in the last inequality we have used the fact that $n-sq<0$. Hence,
\betagin{align*}
\left\|\fracrac{g(y)}{(1+|y|)^{s}}\right\|_{L^{\fracrac{n}{s},\infty}(\mathbb Rn)}
&=\sup_{a>0} a \left|\left\{y\in \mathbb Rn: \fracrac{|g(y)|}{(1+|y|)^s}>a\right\}\right|^{\fracrac{s}{n}}\\
&\leq \sup_{a>0} a \left|\left\{y\in B_1: |g(y)|>a\right\}\right|^{\fracrac{s}{n}}
+C\\
&=\|g\|_{L^{\fracrac{n}{s},\infty}(B_1)} +C\\
&\leq C' \|g\|_{L^q(B_1)}+C\\
&\leq C' \omegaega_n^{\fracrac{1}{q}} M_{L^q}g(0) +C
\leq C^{''},
\end{align*}
where $C'>0$ is the constant from the embedding $L^q(B_1) \hookrightarrow L^{\fracrac{n}{s},\infty}(B_1)$.
Since $M_{L^q}g(0)=1$, this proves~\eqref{E:reduced_inequality}, and in turn~\eqref{E:estimate} as well.
\end{proof}
\betagin{theorem}\labelel{T:endpoint}
Let $p\in (1,\infty)$, $n\in \mathbb N$, $s\in (\fracrac{n}{2},n)$. Let $\Psi$ be as in Theorem~\ref{T:main_theorem}. Then
\betagin{equation}\labelel{E:hormander_lorentz}
\|T_\sigmagma f\|_{L^p(\mathbb Rn)} \leq C \sup_{j\in \mathbb Z} \big\|(I-\Deltalta)^{\fracrac{s}{2}}[\widehat\Psi \sigma(2^j\cdot)\big]\big\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)} \|f\|_{L^p(\mathbb Rn)}.
\end{equation}
\end{theorem}
\betagin{proof}
Let
$$
K=\sup_{j\in \mathbb Z} \big\| (I-\Delta)^{\frac{s }{2}} \big[\widehat{\Psi} \sigma(2^j\cdot)\big]\big\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)} <\infty\, .
$$
Introduce the function $\Theta$ satisfying
$$
\widehat{\Theta}(\xi)=\widehat{\Psi}(\xi/2)+\widehat{\Psi}(\xi)+\widehat{\Psi}(2\xi),
$$
and observe that $\widehat{\Theta}$ is equal to $1$ on the support of the function $\widehat{\Psi}$.
Let us denote by $\Delta_j$ and $\Delta_j^\Theta$ the Littlewood-Paley operators associated with $\Psi$ and $\Theta$, respectively.
If $f$ is a Schwartz function on $\mathbb R^n$, then standard manipulations yield
\betagin{align*}
\Delta_j T_\sigma (f)(x) &= \int_{\mathbb R^n} \widehat{f}(\xi) \widehat{\Psi}(2^{-j} \xi) \sigma(\xi) e^{2\partiali i x\cdot \xi}d\xi
= \int_{\mathbb R^n} (\Delta_j^{\Theta}f )\sphat{}\,(\xi) \widehat{\Psi}(2^{-j} \xi) \sigma(\xi) e^{2\partiali i x\cdot \xi}d\xi\\
&=2^{jn} \int_{\mathbb R^n} (\Delta_j^{\Theta}f )\sphat{}\,(2^{j} \xi') \widehat{\Psi}( \xi') \sigma(2^{j}\xi') e^{2\partiali i x\cdot 2^{j}\xi'} d\xi' \\
&=\int_{\mathbb R^n} (\Delta_j^{\Theta}f )( x+2^{-j}y ) \big[\widehat{\Psi} \sigma(2^{j}\cdot)\big]\sphat\, (y) \, dy\\
&=\int_{\mathbb R^n} \frac{ (\Delta_j^{\Theta}f )( x+2^{-j}y )}{(1+|y|)^s} (1+|y|)^s\big[\widehat{\Psi} \sigma(2^{j}\cdot)\big]\sphat\, ( y) \, dy.
\end{align*}
By the H\"older inequality in Lorentz spaces, we therefore obtain
$$
|\Delta_j T_\sigma (f)(x)|\leq \left\|\frac{(\Delta_j^{\Theta}f )( x+2^{-j}y )}{(1+|y|)^s}\right\|_{L^{\fracrac{n}{s},\infty}(\mathbb Rn)} \left\|(1+|y|)^s\big[\widehat{\Psi} \sigma(2^{j}\cdot)\big]\sphat\, ( y)\right\|_{L^{(\fracrac{n}{s})',1}(\mathbb Rn)}.
$$
Since $\fracrac{n}{s}<2$, we can find a real number $q$ such that $\fracrac{n}{s}<q<2$. Lemma~\ref{L:lemma} now yields that
$$
\left\|\frac{(\Delta_j^{\Theta}f )( x+2^{-j}y )}{(1+|y|)^s}\right\|_{L^{\fracrac{n}{s},\infty}(\mathbb Rn)} \leq C M_{L^q}(\Delta_j^{\Theta} f)(x).
$$
Using boundedness properties of the Fourier transform, we deduce that
\betagin{align*}
\left\|(1+|y|)^s\big[\widehat{\Psi} \sigma(2^{j}\cdot)\big]\sphat\, ( y)\right\|_{L^{(\fracrac{n}{s})',1}(\mathbb Rn)}
&\leq C \left\|(1+|y|^2)^{\fracrac{s}{2}} \big[\widehat{\Psi} \sigma(2^{j}\cdot)\big]\sphat\, ( y)\right\|_{L^{(\fracrac{n}{s})',1}(\mathbb Rn)}\\
&\leq C \big\| (I-\Delta)^{\frac{s }{2}} \big[\widehat{\Psi} \sigma(2^j\cdot)\big]\big\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}
\leq CK.
\end{align*}
Altogether, we obtain the estimate
$$
|\Delta_j T_\sigma (f)|(x) \leq CK M_{L^q}(\Delta_j^{\Theta} f)(x).
$$
Assume that $p\geq 2$.
Then we get, by applying the Littlewood-Paley theorem and the Fefferman-Stein inequality (notice that $\fracrac{p}{q}\geq \fracrac{2}{q}>1$),
\betagin{align*}
\big\| T_\sigma(f) \big\|_{L^p(\mathbb R^n)}
&\le C \Big\| \Big( \sum_{j \in \mathbb Z} |\Delta_j T_\sigma (f) |^2 \Big)^{\frac12} \Big\|_{L^p(\mathbb Rn)}
\leq C K \Big\| \Big( \sum_{j \in \mathbb Z} |M_{L^q}(\Delta_j^{\Theta} f) |^2 \Big)^{\frac12} \Big\|_{L^p(\mathbb Rn)}\\
&=C K \Big\|\Big( \sum_{j \in \mathbb Z} (M (|\Delta_j^{\Theta} f|^q)^{\fracrac{2}{q}}\Big)^{\fracrac{q}{2}} \Big\|_{L^{\fracrac{p}{q}}(\mathbb Rn)}^{\fracrac{1}{q}}
\leq C K \Big\|\Big( \sum_{j \in \mathbb Z} |\Delta_j^{\Theta} f|^{q \cdot \fracrac{2}{q}}\Big)^{\fracrac{q}{2}} \Big\|_{L^{\fracrac{p}{q}}(\mathbb Rn)}^{\fracrac{1}{q}}\\
&= C K \Big\|\Big( \sum_{j \in \mathbb Z} |\Delta_j^{\Theta} f|^{2}\Big)^{\fracrac{1}{2}} \Big\|_{L^{p}(\mathbb Rn)}
\leq C K \|f\|_{L^p(\mathbb Rn)}.
\end{align*}
If $p\in (1,2)$ then the result follows by duality.
\end{proof}
\section{Interpolation}
Our main goal in this section will be to prove the following theorem.
\betagin{theorem}\labelel{T:interpolation}
Suppose that $1<p_1<\infty$ and $0<s_1 <n$. If
\betagin{equation}\labelel{E:assumption}
\|T_\sigma f\|_{L^{p_1}(\mathbb R^n)} \leq C \sup_{j\in \mathbb Z} \|(I-\Delta)^{\fracrac{s_1}{2}}[\widehat{\Psi} \sigma(2^j\cdot)]\|_{L^{\fracrac{n}{s_1},1}(\mathbb R^n)} \|f\|_{L^{p_1}(\mathbb R^n)},
\end{equation}
then
$$
\|T_\sigma f\|_{L^{p}(\mathbb R^n)} \leq C \sup_{j\in \mathbb Z} \|(I-\Delta)^{\fracrac{s}{2}}[\widehat{\Psi} \sigma(2^j\cdot)]\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)} \|f\|_{L^p(\mathbb R^n)}
$$
for any $1<p<\infty$ and $0<s<s_1$ satisfying
\betagin{equation}\labelel{E:assumption_ps}
\fracrac{1}{s}\left|\fracrac{1}{p} - \fracrac{1}{2}\right| <\fracrac{1}{s_1} \left|\fracrac{1}{p_1}-\fracrac{1}{2}\right|.
\end{equation}
\end{theorem}
Assuming Theorem~\ref{T:interpolation}, and using the estimate from Theorem~\ref{T:endpoint} as the assumption~\eqref{E:assumption}, we finish the proof of our main result, Theorem~\ref{T:main_theorem}, as follows.
\betagin{proof}[Proof of Theorem~\ref{T:main_theorem}]
If $s\in (\fracrac{n}{2},n)$, then inequality~\eqref{E:inequality} follows from Theorem~\ref{T:endpoint}. If $s\leq \fracrac{n}{2}$, then we denote
$$
\alphapha=\fracrac{1}{s}\left|\fracrac{1}{p}-\fracrac{1}{2}\right|.
$$
Since $\alphapha \in (0,\fracrac{1}{n})$, we can find $p_1\in (1,\infty)$ and $s_1\in (\fracrac{n}{2},n)$ such that
$$
\alphapha <\fracrac{1}{s_1}\left|\fracrac{1}{p_1}-\fracrac{1}{2}\right|.
$$
A combination of Theorems~\ref{T:endpoint} and~\ref{T:interpolation} thus yields the desired assertion~\eqref{E:inequality}.
\end{proof}
Let us now focus on the proof of Theorem~\ref{T:interpolation}. The main idea of the proof consists in applying a complex interpolation between the estimate~\eqref{E:assumption} and the usual $L^2$ estimate implied by the Plancherel theorem.
To prove Theorem~\ref{T:interpolation} we shall need a few auxiliary results. With start by recalling the classical three lines lemma.
\betagin{lemma}[{\cite{CFA, hirschman}}]\labelel{L:ThreeLines}
Let $F$ be analytic on the open strip $S=\{z\in\mathbb{C}\ :\ 0<\mathbb Re(z)<1\}$ and continuous on its closure.
Assume that for every $0\le \tau \le 1$ there exists a function $A_\tau$ on the { real} line such that
$$
| F(\tau+it) | \le A_\tau(t) \quad\quaduad \textup{ for all $t\in\mathbb{R}$,}
$$
and suppose that there exist constants $A>0$ and $0<a<\partiali$ such that for all $t\in \mathbb R$ we have
$$
0< A_\tau(t) \le \exp \big\{ A e^{a |t|} \big\} \, .
$$
Then for $0<\theta<1 $ we have
$$
\abs{F(\theta )}\le \exp\left\{
\dfracrac{\sigman(\partiali \theta)}{2}\int_{-\infty}^{\infty}\left[
\dfracrac{\log |A_0(t ) | }{\cosh(\partiali t)-\cos(\partiali\theta)}
+
\dfracrac{\log | A_1(t )| }{\cosh(\partiali t)+\cos(\partiali\theta)}
\right]dt
\right\}\, .
$$
\end{lemma}
We point out that in calculations it is crucial to note that
\betagin{equation}\labelel{ide}
\dfracrac{\sigman(\partiali \theta)}{2}\int_{-\infty}^{\infty}
\dfracrac{dt }{\cosh(\partiali t)-\cos(\partiali\theta)} =1-\theta\, , \quad
\dfracrac{\sigman(\partiali \theta)}{2}\int_{-\infty}^{\infty}
\dfracrac{dt }{\cosh(\partiali t)+\cos(\partiali\theta)} = \theta.
\end{equation}
We shall also need the following lemma.
\betagin{lemma}\labelel{L:016}
Let $1<p, p_1<\infty$ be related as in $1/p=(1-\theta)/2+\theta/p_1$ for some $\theta \in (0,1)$.
Given $f\in {\mathscr C}_0^\infty(\mathbb R^n)$ and $\varepsilon>0,$ there exist
smooth functions $h_j^\varepsilon$, $j=1,\dots, N_\varepsilon$, supported in cubes on $\mathbb R^n$ with pairwise disjoint interiors,
and nonzero complex constants $c_j^\varepsilon$ such that the functions
\betagin{equation}\labelel{E:form}
f_z^\varepsilon = \sum_{j=1}^{N_\varepsilon} |c_j^\varepsilon|^{\fracrac p{2} (1-z) + \fracrac p{p_1} z} \, h_j^\varepsilon
\end{equation}
satisfy
$$
\big\|{f_\theta^\varepsilon-f}\big\|_{L^2(\mathbb R^n)}< \varepsilon
$$
and
$$
\|{f_{it}^\varepsilon}\|_{L^{2}(\mathbb R^n)} \leq \left(\|f \|_{L^p(\mathbb R^n)} +\varepsilon\right)^{\fracrac{p}{2}} \, , \quad
\|{f_{1+it}^\varepsilon}\|_{L^{p_1}(\mathbb R^n)}\leq \left(\|f \|_{L^p(\mathbb R^n)} +\varepsilon\right)^{\fracrac{p}{p_1}}\,.
$$
\end{lemma}
\betagin{proof}
Given $f\in {\mathscr C}_0^\infty(\mathbb R^n)$ and $ \varepsilon>0$, by uniform continuity
there are $N_\varepsilon$ cubes $Q_j^\varepsilon$ (with disjoint interiors) and constants $c_j^\varepsilon $ such that
$$
\Big\| f - \sum_{j=1}^{N_\varepsilon} c_j^\varepsilon \chi_{Q_j^\varepsilon} \Big\|_{L^2(\mathbb R^n)} + \Big\| f - \sum_{j=1}^{N_\varepsilon} c_j^\varepsilon \chi_{Q_j^\varepsilon} \Big\|_{L^p(\mathbb R^n)} <\varepsilon \, .
$$
Find nonnegative smooth functions $g_j^\varepsilon\le \chi_{Q_j^\varepsilon}$ such that
$$
\Big\| \sum_{j=1}^{N_\varepsilon} c_j^\varepsilon ( g_j^\varepsilon- \chi_{Q_j^\varepsilon} ) \Big\|_{L^2(\mathbb R^n)} + \Big\| \sum_{j=1}^{N_\varepsilon} c_j^\varepsilon ( g_j^\varepsilon- \chi_{Q_j^\varepsilon} ) \Big\|_{L^p(\mathbb R^n)} <\varepsilon.
$$
Let $\partialhi_j^\varepsilon$ be the argument of the complex number $c_j^\varepsilon$.
Set $h_j^\varepsilon = e^{i\partialhi_j^\varepsilon} g_j^\varepsilon$ and
notice that
$ f_\theta^\varepsilon = \sum_{j=1}^{N_\varepsilon} |c_j^\varepsilon| h_j^\varepsilon = \sum_{j=1}^{N_\varepsilon} c_j^\varepsilon g_j^\varepsilon $ satisfies
$$
\big\|{f_\theta^\varepsilon-f}\big\|_{L^2(\mathbb R^n)} + \big\|{f_\theta^\varepsilon-f}\big\|_{L^p(\mathbb R^n)}< \varepsilon .
$$
We also observe that
\betagin{align*}
\|f_{it}^\varepsilon\|_{L^2(\mathbb R^n)}^2
&=\|f_{1+it}^\varepsilon\|_{L^{p_1}(\mathbb R^n)}^{p_1}=\|f_\theta^\varepsilon\|_{L^p(\mathbb R^n)}^p\\
&\leq \left(\|f_\theta^\varepsilon - f\|_{L^p(\mathbb R^n)} +\|f\|_{L^p(\mathbb R^n)}\right)^p \leq
\left(\|f\|_{L^p(\mathbb R^n)}+\varepsilon\right)^p,
\end{align*}
as claimed.
\end{proof}
The next three lemmas generalize results which are well known in the context of Lebesgue spaces into the setting of Lorentz spaces $L^{p,1}(\mathbb R^n)$.
\betagin{lemma}\labelel{L:sobolev_embedding}
Let $0<s<n$. Then
$$
\|(I-\Delta)^{-\fracrac{s}{2}} f\|_{L^\infty(\mathbb R^n)} \leq C(n) \fracrac{s}{n-s} \|f\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}.
$$
\end{lemma}
\betagin{proof}
Let $G_s$ be the function defined for any $x\in \mathbb R^n$ by
$$
G_s(x)=\fracrac{1}{(4\partiali)^{\fracrac{s}{2}}\Gamma(\fracrac{s}{2})} \int_0^\infty e^{-\fracrac{\partiali|x|^2}{\deltalta}} e^{-\fracrac{\deltalta}{4\partiali}} \deltalta^{\fracrac{-n+s}{2}} \fracrac{\,d\deltalta}{\deltalta}.
$$
It is not difficult to show that $G_s(x)\leq C(n)\fracrac{s}{n-s} |x|^{-n+s}$. Therefore,
\betagin{align*}
|(I-\Delta)^{-\fracrac{s}{2}} f(x)|=|G_s\ast f(x)|
&\leq \int_{\mathbb R^n} G_s(y) |f(x-y)|\,dy
\leq \|G_s\|_{L^{(\fracrac{n}{s})',\infty}(\mathbb R^n)} \|f\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}\\
&\leq C(n) \fracrac{s}{n-s} \|f\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}.
\end{align*}
\end{proof}
\betagin{lemma}\labelel{L:interpolation}
Let $1<a<b<\infty$. Then, for any $p\in (a,b)$ and any $t\in \mathbb R$,
$$
\|(I-\Delta)^{-it}f\|_{L^{p,1}(\mathbb R^n)} \leq C(n,a,b) (1+|t|)^{\fracrac{n}{2}+1} \|f\|_{L^{p,1}(\mathbb R^n)}.
$$
\end{lemma}
\betagin{proof}
Set $b_0=2b$. By the H\"ormander multiplier theorem, one has
$$
\|(I-\Delta)^{-it}f\|_{L^{1,\infty}(\mathbb R^n)} \leq C(n) (1+|t|)^{\fracrac{n}{2}+1} \|f\|_{L^{1}(\mathbb R^n)}
$$
and
$$
\|(I-\Delta)^{-it}f\|_{L^{b_0}(\mathbb R^n)} \leq C(n,b) (1+|t|)^{\fracrac{n}{2}+1} \|f\|_{L^{b_0}(\mathbb R^n)}.
$$
Notice that the second estimate implies, in particular, the corresponding weak-type inequality. An interpolation between these two estimates using the Marcinkiewicz interpolation theorem~\cite[Chapter 4, Theorem 4.13]{BS} yields the required assertion.
\end{proof}
\betagin{lemma}\labelel{L:interpolation2}
Let $1<p<\infty$ and $s>0$, and let $\Psi$ be as in Theorem~\ref{T:main_theorem}. Then we have the a priori estimate
\betagin{equation}\labelel{E:kato_ponce}
\|(I-\Delta)^{\fracrac{s}{2}}[\widehat{\Psi}f]\|_{L^{p,1}(\mathbb R^n)} \leq C(n,s,p,\Psi) \|(I-\Delta)^{\fracrac{s}{2}}f\|_{L^{p,1}(\mathbb R^n)}.
\end{equation}
\end{lemma}
\betagin{proof}
Pick real numbers $p_0$, $p_1$ satisfying $1<p_0<p<p_1<\infty$. Denote by $T$ the linear operator defined by
$$
Tf=(I-\Deltalta)^{\fracrac{s}{2}} [\widehat{\Psi}(I-\Deltalta)^{-\fracrac{s}{2}}f].
$$
Thanks to the Kato-Ponce inequality, $T$ is bounded on both $L^{p_0}(\mathbb R^n)$ and $L^{p_1}(\mathbb R^n)$, so, in particular, it is of weak type $(p_0,p_0)$ and $(p_1,p_1)$.
By the Marcinkiewicz interpolation theorem~\cite[Chapter 4, Theorem 4.13]{BS}, $T$ is bounded on $L^{p,1}(\mathbb R^n)$, which yields~\eqref{E:kato_ponce}.
\end{proof}
The final auxiliary result we shall need is the following.
\betagin{lemma}\labelel{L:fractional_maximal_function}
Let $0<a<s<n$. Then
\betagin{equation}\labelel{E:sunrise}
\int_0^\infty (f^*(r) r^{\fracrac{s-a}{n}})^*(y) y^{\fracrac{a}{n}-1}\,dy \leq \fracrac{C(n)}{a} \int_0^\infty f^*(r) r^{\fracrac{s}{n}-1}\,dr.
\end{equation}
\end{lemma}
\betagin{proof}
Estimates of this type are known in the literature, see, e.g., \cite{EO}. For the convenience of the reader, we also provide an elementary proof of inequality~\eqref{E:sunrise}. The proof follows the ideas of~\cite[Section 9]{CPS}.
We may assume that
$$
\int_0^\infty f^*(r) r^{\fracrac{s}{n}-1}\,dr <\infty.
$$
Then $f^*(r) r^{\fracrac{s}{n}}\leq C$, and thus $L^{\infty}m_{r\to \infty} f^*(r) r^{\fracrac{s-a}{n}}=0$. Since the function $f^*$ is left-continuous, $\sup_{y\leq r<\infty} f^*(r) r^{\fracrac{s-a}{n}}$ is attained for any $y>0$ and the set
$$
M=\{y\in (0,\infty): \sup_{y\leq r<\infty} f^*(r) r^{\fracrac{s-a}{n}} > f^*(y) y^{\fracrac{s-a}{n}}\}
$$
is open. Hence, $M$ is a countable union of open intervals, namely, $M=\bigcup_{k\in S} (a_k,b_k)$, where $S$ is a countable set of positive integers. Also, observe that if $y\in (a_k,b_k)$, then $\sup_{y\leq r<\infty} f^*(r) r^{\fracrac{s-a}{n}}=f^*(b_k) b_k^{\fracrac{s-a}{n}}$. We have
\betagin{align*}
\int_0^\infty (f^*(r) r^{\fracrac{s-a}{n}})^*(y) y^{\fracrac{a}{n}-1}\,dy
&\leq \int_0^\infty \sup_{y\leq r<\infty} f^*(r) r^{\fracrac{s-a}{n}} y^{\fracrac{a}{n}-1}\,dy\\
&=\int_{(0,\infty)\setminus \cup_{k\in S} (a_k,b_k)} f^*(y) y^{\fracrac{s}{n}-1}\,dy
+\sum_{k\in S} f^*(b_k) b_k^{\fracrac{s-a}{n}} \int_{a_k}^{b_k} y^{\fracrac{a}{n}-1}\,dy.
\end{align*}
Furthermore, for every $k\in S$,
\betagin{align*}
f^*(b_k) b_k^{\fracrac{s-a}{n}} \int_{a_k}^{b_k} y^{\fracrac{a}{n}-1}\,dy
&\leq f^*(b_k) b_k^{\fracrac{s-a}{n}}\int_{\max(a_k,\fracrac{b_k}{2})}^{b_k} y^{\fracrac{a}{n}-1}\,dy \cdot \fracrac{\int_0^{b_k} y^{\fracrac{a}{n}-1}\,dy}{\int_{\fracrac{b_k}{2}}^{b_k} y^{\fracrac{a}{n}-1}\,dy}\\
&=\fracrac{1}{1-(\fracrac{1}{2})^{\fracrac{a}{n}}} f^*(b_k) b_k^{\fracrac{s-a}{n}} \int_{\max(a_k,\fracrac{b_k}{2})}^{b_k} y^{\fracrac{a}{n}-1}\,dy\\
&\leq \fracrac{2^{\fracrac{s-a}{n}}}{1-(\fracrac{1}{2})^{\fracrac{a}{n}}} \int_{a_k}^{b_k} f^*(y) y^{\fracrac{s}{n}-1}\,dy\\
&\leq \fracrac{C(n)}{a} \int_{a_k}^{b_k} f^*(y) y^{\fracrac{s}{n}-1}\,dy.
\end{align*}
Therefore,
\betagin{align*}
\int_0^\infty (f^*(r) r^{\fracrac{s-a}{n}})^*(y) y^{\fracrac{a}{n}-1}\,dy
&\leq \int_0^\infty f^*(y) y^{\fracrac{s}{n}-1}\,dy +\fracrac{C(n)}{a} \sum_{k\in S} \int_{a_k}^{b_k} f^*(y) y^{\fracrac{s}{n}-1}\,dy\\
&\leq \fracrac{C(n)}{a} \int_0^\infty f^*(y) y^{\fracrac{s}{n}-1}\,dy.
\end{align*}
\end{proof}
We are now in a position to prove Theorem~\ref{T:interpolation}. We shall need the notion of a measure preserving transformation. We say that a mapping $h: \mathbb R^n \rightarrow (0,\infty)$ is measure preserving if, whenever $E$ is a measurable subset of $(0,\infty)$, the set $h^{-1}E=\{x\in \mathbb R^n: h(x)\in E\}$ is a measurable subset of $\mathbb R^n$ and the $n$-dimensional Lebesgue measure of $h^{-1}E$ is equal to the one-dimensional Lebesgue measure of $E$. For more details on measure preserving transformations, see, e.g., \cite[Chapter 2, Section 7]{BS}.
\betagin{proof}[Proof of Theorem~\ref{T:interpolation}]
We first observe that, by~\eqref{E:assumption_ps}, we have $p_1\neq 2$. In fact, we can assume that $1<p_1<2$ and $1<p\leq 2$, otherwise the result will follow by duality. Further, if $p=2$ then Theorem~\ref{T:interpolation} is a consequence of Plancherel's theorem and of the Sobolev embedding from Lemma~\ref{L:sobolev_embedding}, so it is sufficient to focus on the case $p<2$ in what follows. Define
$$
\theta=\fracrac{\fracrac{1}{p}-\fracrac{1}{2}}{\fracrac{1}{p_1}-\fracrac{1}{2}}.
$$
The assumption~\eqref{E:assumption_ps} yields $\theta \in (0,\fracrac{s}{s_1})$, and therefore
$$
\theta = \fracrac{s-s_0}{s_1-s_0}
$$
for some $s_0\in (0,s)$. Fix a function $\sigma$ satisfying
\betagin{equation}\labelel{E:assumption_si}
\sup_{j\in \mathbb Z} \|(I-\Delta)^{\fracrac{s}{2}}[\widehat{\Psi} \sigma(2^j\cdot)]\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}<\infty,
\end{equation}
and denote $\varphi_j=(I-\Delta)^{\fracrac{s}{2}}[\widehat{\Psi} \sigma(2^j\cdot)]$, $j\in \mathbb Z$. Thanks to~\eqref{E:assumption_si}, we have $L^{\infty}m_{r\to \infty} \varphi_j^*(r)=0$. By~\cite[Chapter 2, Corollary 7.6]{BS}, there is a measure preserving transformation $h_j: \mathbb R^n \rightarrow (0,\infty)$ such that $|\varphi_j|=\varphi_j^* \circ h_j$.
For a complex number $z$ with $0\leq \mathbb Re(z)\leq 1$, we define
\betagin{equation}\labelel{E:definition}
\sigma_z(\xi)
=\sum_{j\in \mathbb Z} (I - \Delta)^{-\fracrac{s_0(1-z)+s_1z}{2}} [\varphi_j h_j^{\fracrac{s-(1-z)s_0-zs_1}{n}}](2^{-j}\xi) \widehat{\Phi}(2^{-j}\xi),
\end{equation}
where $\widehat{\Phi}$ is a Schwartz function supported in the set $\{\xi \in \mathbb R^n: \fracrac{1}{4} \leq |\xi| \leq 4\}$ and $\widehat{\Phi}\equiv 1$ on the support of $\widehat{\Psi}$.
Fix $f, g\in \mathscr C_0^\infty$. Given $\varepsilon>0$, let $f_z^\varepsilon$ and $g_z^\varepsilon$ be functions having the form~\eqref{E:form}, with $f$ replaced by $g$ and with $p$ replaced by $p'$ in the latter case, satisfying
$ \norm{f_\theta^\varepsilon-f}_{L^2(\mathbb R^n)}<\varepsilon$, $ \norm{g_\theta^\varepsilon-g}_{L^{2}(\mathbb R^n)}<\varepsilon, $
and
\betagin{align}\labelel{E:fg}
& \norm{f_{it}^\varepsilon}_{L^{2}(\mathbb R^n)}\le \big( \norm{f}_{L^{p}(\mathbb R^n)}+\varepsilon\big)^{\fracrac {p}{2}} ,\quad
\norm{f_{1+it}^\varepsilon}_{L^{p_1}(\mathbb R^n)}\le \big( \norm{f}_{L^{p}(\mathbb R^n)}+\varepsilon\big)^{\fracrac {p}{p_1}},\\
\nonumber
& \norm{g_{it}^\varepsilon}_{L^{2}(\mathbb R^n)}\le \big( \norm{g}_{L^{p'}(\mathbb R^n)}+\varepsilon\big)^{\fracrac {p'}{2}},\quad
\norm{g_{1+it}^\varepsilon}_{L^{p_1'}(\mathbb R^n)}\le \big( \norm{g}_{L^{p'}(\mathbb R^n)}+\varepsilon\big)^{\fracrac {p'}{p_1'}}.
\end{align}
Recall that the existence of these functions is guaranteed by Lemma \ref{L:016}.
For a complex number $z$ with $0\leq \mathbb Re(z) \leq 1$, define
\betagin{align*}
F(z) =& \int_{\mathbb R^n} T_{\sigmagma_z}(f_z^\varepsilon) {g}_z^\varepsilon\; dx
=\int_{\mathbb R^n} \sigma_z(\xi) \widehat{f^{\varepsilon}_{z}}(\xi) \widehat{g^{\varepsilon}_{z}}(\xi)\, d\xi.
\end{align*}
It is straightforward (but rather tedious) to verify
that $F$ is analytic on the strip $S=\{z\in \mathcal C: 0 <\mathbb Re(z)<1\}$ and continuous on its closure.
\betagin{comment}
------------------------------ PROOF OF THE ANALYTICITY -------------------------------
By Lemma~\ref{L:016}, the functions $f_z^\varepsilon$ and $g_z^\varepsilon$ have the form
$$
f^\varepsilon_z=\sum_{\ell=1}^{N_\varepsilon} |c_\ell^\varepsilon|^{(1-z)\cdot \fracrac{p}{2}+z\cdot \fracrac{p}{p_1}} u_\ell^\varepsilon,
$$
$$
g^\varepsilon_z=\sum_{k=1}^{M_\varepsilon} |d_k^\varepsilon|^{(1-z)\cdot \fracrac{p'}{2}+z\cdot \fracrac{p'}{p_1'}} v_k^\varepsilon,
$$
where $u_\ell^\varepsilon$ and $v_k^\varepsilon$ are Schwartz functions.
Therefore,
$$
F(z)=\sum_{\ell=1}^{N_\varepsilon} \sum_{k=1}^{M_\varepsilon} |c_\ell^\varepsilon|^{(1-z)\cdot \fracrac{p}{2}+z\cdot \fracrac{p}{p_1}} |d_k^\varepsilon|^{(1-z)\cdot \fracrac{p'}{2}+z\cdot \fracrac{p'}{p_1'}}
\int_{\mathbb R^n} \sigmagma_z(\xi) \widehat{u_\ell^\varepsilon}(\xi) \widehat{v_k^\varepsilon}(\xi)\,d\xi.
$$
Thus, to prove that $F$ is analytic on the strip $S$, it suffices to show that the function
\betagin{equation}\labelel{E:function}
z\mapsto \int_{\mathbb R^n} \sigmagma_z(\xi) \widehat{u_\ell^\varepsilon}(\xi) \widehat{v_k^\varepsilon}(\xi)\,d\xi
\end{equation}
is analytic on $S$ for every $\ell=1,\dots,N_\varepsilon$ and every $k=1,\dots,M_\varepsilon$.
\betagin{lemma}\labelel{L:analytic}
Given $j\in \mathbb Z$, denote
$$
H^j(z,x)=(I-\Deltalta)^{-\fracrac{s_0(1-z)+s_1z}{2}}[\varphi_j \cdot h_j^{\fracrac{s-(1-z)s_0-zs_1}{n}}](x), \quad z\in S, ~x\in \mathbb R^n.
$$
Then $H^j(\cdot,x)$ is analytic on $S$ for every $x\in \mathbb R$. Also, if $w\in S$ and $r>0$ are such that $B_r(w)=\{z\in \mathcal C: |z-w|\leq r\} \subseteq S$, then there is a function $H^j_*(x)$ (depending also on $r$, $w$, $s_0$, $s_1$ and $n$) such that
$$
|H^j(z,x)|+\left|\fracrac{\partialartial}{\partialartial z} H^j(z,x)\right|\leq H^j_*(x), \quad z\in B_r(w), ~x\in \mathbb R^n,
$$
and
\betagin{equation}\labelel{E:uniform_integrability}
\int_{\{x\in \mathbb R^n: \fracrac{1}{4}\leq |x|\leq 4\}} H^j_*(x)\,dx \leq C,
\end{equation}
where $C$ depends on $s_0$, $s_1$, $w$, $r$, $n$, but is independent of $j$.
\end{lemma}
\betagin{proof}
Given a complex number $\alphapha$ with $\mathbb Re(\alphapha)>0$, we set
$$
G_\alphapha(x)=\fracrac{1}{(4\partiali)^{\fracrac{\alphapha}{2}}\Gamma(\fracrac{\alphapha}{2})} \int_0^\infty e^{-\fracrac{\partiali|x|^2}{\deltalta}} e^{-\fracrac{\deltalta}{4\partiali}} \deltalta^{\fracrac{-n+\alphapha}{2}} \fracrac{\,d\deltalta}{\deltalta}.
$$
Then
$$
\widehat{G_\alphapha}(x)=(1+4\partiali^2 |x|^2)^{-\fracrac{\alphapha}{2}},
$$
and therefore
$$
H^j(z,x)=G_{s_0(1-z)+s_1z} \ast (\varphi_j h_j^{\fracrac{s-(1-z)s_0-zs_1}{n}})(x), \quad x\in \mathbb R^n.
$$
Let $\varepsilon>0$ be such that $\varepsilon<s_0$ and $s_1+\varepsilon<n$. Then
\betagin{align*}
&|G_{s_0(1-z)+s_1z}(y)| +\left|\fracrac{\partialartial}{\partialartial z} G_{s_0(1-z)+s_1z}(y)\right|\\
&\leq C(s_0,s_1,w,r)\left(\int_0^1 e^{-\fracrac{\partiali|y|^2}{\deltalta}} e^{-\fracrac{\deltalta}{4\partiali}} \deltalta^{\fracrac{-n+s_0}{2}} \log \fracrac{e}{\deltalta} \fracrac{\,d\deltalta}{\deltalta}
+\int_1^\infty e^{-\fracrac{\partiali|y|^2}{\deltalta}} e^{-\fracrac{\deltalta}{4\partiali}} \deltalta^{\fracrac{-n+s_1}{2}} \log(e\deltalta) \fracrac{\,d\deltalta}{\deltalta}\right)\\
&\leq C(s_0,s_1,w,r,\varepsilon) \left(\int_0^\infty e^{-\fracrac{\partiali|y|^2}{\deltalta}} e^{-\fracrac{\deltalta}{4\partiali}} \deltalta^{\fracrac{-n+s_0-\varepsilon}{2}} \fracrac{\,d\deltalta}{\deltalta}
+\int_0^\infty e^{-\fracrac{\partiali|y|^2}{\deltalta}} e^{-\fracrac{\deltalta}{4\partiali}} \deltalta^{\fracrac{-n+s_1+\varepsilon}{2}} \fracrac{\,d\deltalta}{\deltalta}\right)\\
&\leq C(s_0,s_1,w,r,\varepsilon) \left(\chi_{\{x\in \mathbb R^n: |x|<1\}}(y) (|y|^{-n+s_0-\varepsilon} +|y|^{-n+s_1+\varepsilon}) +\chi_{\{x\in \mathbb R^n: |x|\geq 1\}}(y) e^{-|y|/2}\right)\\
&\leq C(s_0,s_1,w,r,\varepsilon) \left(\chi_{\{x\in \mathbb R^n: |x|<1\}}(y) |y|^{-n+s_0-\varepsilon} +\chi_{\{x\in \mathbb R^n: |x|\geq 1\}}(y) e^{-|y|/2}\right),
\quad z\in B_r(w).
\end{align*}
Notice that to derive the first inequality, we used the fact that the function $\Gamma$ is positive and continuous on the closed bounded set $A:=\fracrac{s_0}{2}(1-B_r(w))+\fracrac{s_1}{2} B_r(w)$, which yields that $1/\Gamma$ is bounded on $A$, and that $\Gamma'$ is continuous, and thus bounded, on $A$.
Further,
\betagin{align*}
&|h_j^{\fracrac{s-(1-z)s_0-zs_1}{n}}(y)|+\left|\fracrac{\partialartial}{\partialartial z} h_j^{\fracrac{s-(1-z)s_0-zs_1}{n}}(y)\right|\\
&\leq C(s_0,s_1,n) |h_j^{\fracrac{s-(1-z)s_0-zs_1}{n}}(y)| (1+|\log h_j|)\\
&\leq C(s_0,s_1,n) \chi_{\{x: h_j(x)<1\}}(y) \log \fracrac{e}{h_j}(y) h_j^{\fracrac{s-s_1}{n}}(y)
+C(s_0,s_1,n) \chi_{\{x: h_j(x)\geq 1\}}(y) \log (eh_j) (y) h_j^{\fracrac{s-s_0}{n}}(y)\\
&\leq C(s_0,s_1,n) \chi_{\{x: h_j(x)<1\}}(y) h_j^{\fracrac{s-n}{n}}(y)
+C(s_0,s_1,n) \chi_{\{x: h_j(x)\geq 1\}}(y) h_j^{\fracrac{s}{n}}(y)\\
&\leq C(s_0,s_1,n) (h_j^{\fracrac{s}{n}-1}(y) +h_j^{\fracrac{s}{n}}(y)).
\end{align*}
Thus,
\betagin{align*}
&|H^j(z,x)|+\left|\fracrac{\partialartial}{\partialartial z} H^j(z,x)\right|\\
&\leq \left(|G_{s_0(1-z)+s_1z}| +\left|\fracrac{\partialartial}{\partialartial z} G_{s_0(1-z)+s_1z}\right|\right) \ast \left(|\varphi_j h_j^{\fracrac{s-(1-z)s_0-zs_1}{n}}|+\left|\varphi_j \fracrac{\partialartial}{\partialartial z} h_j^{\fracrac{s-(1-z)s_0-zs_1}{n}}\right|\right)(x)\\
&\leq C(s_0,s_1,w,r,n,\varepsilon) (|y|^{-n+s_0-\varepsilon} \chi_{\{x: |x|<1\}}(y) +\chi_{\{x: |x|\geq 1\}}(y) e^{-\fracrac{|y|}{2}}) \ast (|\varphi_j(y)| (h_j^{\fracrac{s-n}{n}}(y)+h_j^{\fracrac{s}{n}}(y))(x)\\
&=H^j_*(x).
\end{align*}
Hence, using the estimates
$$
\|f\ast g\|_{L^1(\mathbb R^n)} \leq \|f\|_{L^1(\mathbb R^n)} \|g\|_{L^1(\mathbb R^n)} \quad \textup{and} \quad |f\ast g|(x)\leq \|f\|_{L^1(\mathbb R^n)} \|g\|_{L^\infty(\mathbb R^n)},
$$
we obtain
\betagin{align*}
&\int_{\{x\in \mathbb R^n: \fracrac{1}{4}\leq |x|\leq 4\}} H_*^j(x)\,dx\\
&\leq C(s_0,s_1,w,r,n,\varepsilon) \int_{\mathbb R^n} \left(|y|^{-n+s_0-\varepsilon} \chi_{\{x: |x|<1\}}(y) +\chi_{\{x: |x|\geq 1\}}(y) e^{-\fracrac{|y|}{2}}\right)\,dy
\cdot \int_{\mathbb R^n} |\varphi_j(y)| h_j^{\fracrac{s-n}{n}}(y)\,dy\\
&+C(s_0,s_1,w,r,n,\varepsilon) \int_{\mathbb R^n} \left(|y|^{-n+s_0-\varepsilon} \chi_{\{x: |x|<1\}}(y) +\chi_{\{x: |x|\geq 1\}}(y) e^{-\fracrac{|y|}{2}}\right)\,dy
\cdot \sup_{y\in \mathbb R^n} |\varphi_j(y)| h_j^{\fracrac{s}{n}}(y)\\
&\leq C(s_0,s_1,w,r,n) \left(\int_0^\infty \varphi_j^*(r) r^{\fracrac{s}{n}-1}\,dr +\sup_{t\in (0,\infty)} \varphi_j^*(t) t^{\fracrac{s}{n}}\right)\\
&\leq C(s_0,s_1,w,r,n) \left(\int_0^\infty \varphi_j^*(r) r^{\fracrac{s}{n}-1}\,dr + \sup_{t\in (0,\infty)} \int_{\fracrac{t}{2}}^t \varphi_j^*(r) r^{\fracrac{s}{n}-1}\,dr\right)\\
&\leq C(s_0,s_1,w,r,n) \sup_{j\in \mathbb Z} \|\varphi_j\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)} \leq C.
\end{align*}
\end{proof}
Let us observe that
$$
\sigmagma_z(\xi)=\sum_{j\in \mathbb Z} H^j(z,2^{-j}\xi) \widehat{\Phi}(2^{-j}\xi).
$$
By Lemma~\ref{L:analytic}, $\sigmagma_z(\xi)$ is analytic on $S$ for every $\xi \in \mathbb R$ and
\betagin{align*}
|\sigmagma_z(\xi)|+\left|\fracrac{\partialartial}{\partialartial z} \sigmagma_z(\xi)\right|
&\leq \sum_{j\in \mathbb Z} (|H^j(z,2^{-j}\xi)|+\left|\fracrac{\partialartial}{\partialartial z} H^j(z,2^{-j}\xi)\right|)\widehat{\Phi}(2^{-j}\xi)\\
&\leq \sum_{j\in \mathbb Z} H^j_*(2^{-j}\xi) \widehat{\Phi}(2^{-j}\xi), \quad z\in B_r(w).
\end{align*}
Notice that the right-hand side of the previous inequality is independent of $z$.
Since $\widehat{u_\ell^\varepsilon}$, $\widehat{v_k^\varepsilon}$ are Schwartz functions, we have the estimates
$$
|\widehat{u_j^\varepsilon}(\xi)|\leq \fracrac{C}{|\xi|^n}, \quad |\widehat{v_k^\varepsilon}(\xi)|\leq \fracrac{C}{|\xi|^n}, \quad |\xi|\geq 1,
$$
$$
|\widehat{u_j^\varepsilon}(\xi)|\leq C, \quad |\widehat{v_k^\varepsilon}(\xi)|\leq C, \quad |\xi|\leq 1.
$$
Hence, using also~\eqref{E:uniform_integrability}, for any $z\in B_r(w)$ we have
\betagin{align*}
&\int_{\mathbb R^n} \left(|\sigmagma_z(\xi)|+\left|\fracrac{\partialartial}{\partialartial z} \sigmagma_z(\xi)\right|\right) |\widehat{u_\ell^\varepsilon}(\xi)| |\widehat{v_k^\varepsilon}(\xi)|\,d\xi\\
&\leq \int_{\mathbb R^n} \sum_{j\in \mathbb Z} H^j_*(2^{-j}\xi) \widehat{\Phi}(2^{-j}\xi) |\widehat{u_\ell^\varepsilon}(\xi)| |\widehat{v_k^\varepsilon}(\xi)|\,d\xi\\
&\leq C \sum_{j\in \mathbb Z} \int_{\{\fracrac{1}{4}\leq 2^{-j}|\xi|\leq 4\}} H^j_*(2^{-j}\xi) |\widehat{u_\ell^\varepsilon}(\xi)| |\widehat{v_k^\varepsilon}(\xi)|\,d\xi\\
&\leq C \sum_{j\in \mathbb Z} 2^{jn} \int_{\{\fracrac{1}{4}\leq |x|\leq 4\}} H^j_*(x) |\widehat{u_\ell^\varepsilon}(2^j x)| |\widehat{v_k^\varepsilon}(2^j x)|\,dx\\
&\leq C \sum_{j\in \mathbb Z_{-}} 2^{jn} C(s_0,s_1,w,r,n) + C \sum_{j\in \mathbb Z^{+}_{0}} 2^{-jn} C(s_0,s_1,w,r,n)\\
&\leq C'(s_0,s_1,w,r,n).
\end{align*}
This proves that the function from~\eqref{E:function} is analytic on $S$, which, in turn, yields the analyticity of $F$.
---------------- PROOF OF THE ANALYTICITY - END ---------------------------------
\end{comment}
Let us write $z=\tau +it$, $0\leq \tau \leq 1$ and $t\in \mathbb R$, and denote $s_\tau=s_0(1-\tau)+s_1\tau$. Then, applying Lemmas~\ref{L:sobolev_embedding} and \ref{L:interpolation} and using the fact that $h_j$ is measure preserving, we obtain
\betagin{align*}
\|\sigma_z\|_{L^\infty(\mathbb R^n)}
&\leq C(n) \sup_{j\in \mathbb Z} \|(I-\Delta)^{-\fracrac{s_0(1-z)+s_1z}{2}}[\varphi_j h_j^{\fracrac{s-(1-z)s_0-zs_1}{n}}]\|_{L^\infty(\mathbb R^n)}\\
&\leq C(n) \fracrac{s_\tau}{n-s_\tau} \sup_{j\in \mathbb Z} \|(I-\Delta)^{-\fracrac{s_0(-it)+s_1it}{2}}[\varphi_j h_j^{\fracrac{s-(1-\tau-it)s_0-(\tau+it)s_1}{n}}]\|_{L^{\fracrac{n}{s_\tau},1}(\mathbb R^n)}\\
&\leq C(n,s_0,s_1) \fracrac{s_\tau}{n-s_\tau} (1+|t|)^{\fracrac{n}{2}+1} \sup_{j\in \mathbb Z} \|\varphi_j h_j^{\fracrac{s-(1-\tau-it)s_0-(\tau+it)s_1}{n}}\|_{L^{\fracrac{n}{s_\tau},1}(\mathbb R^n)}\\
&\leq C(n,s_0,s_1) (1+|t|)^{\fracrac{n}{2}+1} \sup_{j\in \mathbb Z} \|\varphi_j^*(r) r^{\fracrac{s-(1-\tau)s_0-\tau s_1}{n}}\|_{L^{\fracrac{n}{s_\tau},1}(0,\infty)}\\
&\leq C(n,s_0,s_1) (1+|t|)^{\fracrac{n}{2}+1} \sup_{j\in \mathbb Z} \|\varphi_j^*\|_{L^{\fracrac{n}{s},1}(0,\infty)}\\
&\leq C(n,s_0,s_1) (1+|t|)^{\fracrac{n}{2}+1} \sup_{j\in \mathbb Z} \|\varphi_j\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}.
\end{align*}
Notice that if $\tau \in [0,\theta)$, then the last but one inequality follows from Lemma~\ref{L:fractional_maximal_function}.
Therefore,
\betagin{align}\labelel{E:l_infty_estimate}
|F(z)|&\leq \|\sigma_z\|_{L^\infty(\mathbb R^n)} \|f^\varepsilon_z\|_{L^2(\mathbb R^n)} \|g^\varepsilon_z\|_{L^2(\mathbb R^n)}\\
\nonumber
&\leq C(n,s_0,s_1) (1+|t|)^{\fracrac{n}{2}+1} \sup_{j\in \mathbb Z} \|\varphi_j\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)} \|f^\varepsilon_z\|_{L^2(\mathbb R^n)} \|g^\varepsilon_z\|_{L^2(\mathbb R^n)}.
\end{align}
Since $\|f^\varepsilon_z\|_{L^2(\mathbb R^n)} \|g^\varepsilon_z\|_{L^2(\mathbb R^n)}$ can be bounded from above by a constant independent of $z$, the previous estimate yields
\betagin{equation}\labelel{E:assumption_interpolation}
|F(z)|\leq C(n,s_0,s_1,p,p_1,\varepsilon,f,g) (1+|t|)^{\fracrac{n}{2}+1} \sup_{j\in \mathbb Z} \|\varphi_j\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)} \leq \exp\{A e^{a|t|}\}
\end{equation}
for a suitable choice of constants $A>0$ and $a\in (0,\partiali)$.
Also, if $z=it$, $t\in \mathbb R$, then~\eqref{E:l_infty_estimate} combined with~\eqref{E:fg} yield
\betagin{equation}\labelel{E:endpoint0}
|F(it)|\leq C(n,s_0,s_1) (1+|t|)^{\fracrac{n}{2}+1} \big( \norm{f}_{L^{p}(\mathbb R^n)}+\varepsilon\big)^{\fracrac p{2}} \big( \norm{g}_{L^{p'}(\mathbb R^n)}+\varepsilon\big)^{\fracrac{p'}{2}} \sup_{j\in \mathbb Z} \|\varphi_j\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}.
\end{equation}
Finally, by the H\"older inequality and by~\eqref{E:assumption},
\betagin{align*}
|F(1+it)|&\leq \|T_{\sigma_{1+it}}(f^\varepsilon_{1+it})\|_{L^{p_1}(\mathbb R^n)} \|g^\varepsilon_{1+it}\|_{L^{p'_1}(\mathbb R^n)}\\
&\leq C\sup_{j\in \mathbb Z} \|(I-\Delta)^{\fracrac{s_1}{2}} [\widehat{\Psi} \sigma_{1+it}(2^j\cdot )]\|_{L^{\fracrac{n}{s_1},1}(\mathbb R^n)} \|f^\varepsilon_{1+it}\|_{L^{p_1}(\mathbb R^n)} \|g^\varepsilon_{1+it}\|_{L^{p'_1}(\mathbb R^n)}.
\end{align*}
Notice that $\widehat{\Psi} \sigma_{1+it}(2^k\cdot )$ picks up only those terms $j$ of~\eqref{E:definition} which differ from $k$ by at most two units. For simplicity, we may therefore take $j=k$ in the calculation below. We have
\betagin{align*}
&\|(I-\Delta)^{\fracrac{s_1}{2}} [\widehat{\Psi}(I - \Delta)^{-\fracrac{s_1+it(s_1-s_0)}{2}} [\varphi_j h_j^{\fracrac{s-s_1+it(s_0-s_1)}{n}}]]\|_{L^{\fracrac{n}{s_1},1}(\mathbb R^n)}\\
&\leq C \|(I-\Delta)^{\fracrac{s_1}{2}} [(I - \Delta)^{-\fracrac{s_1+it(s_1-s_0)}{2}} [\varphi_j h_j^{\fracrac{s-s_1+it(s_0-s_1)}{n}}]]\|_{L^{\fracrac{n}{s_1},1}(\mathbb R^n)}\\
&\leq C\|(I - \Delta)^{-\fracrac{it(s_1-s_0)}{2}} [\varphi_j h_j^{\fracrac{s-s_1+it(s_0-s_1)}{n}}]\|_{L^{\fracrac{n}{s_1},1}(\mathbb R^n)}\\
&\leq C (1+|t|)^{\fracrac{n}{2}+1}\|\varphi_j h_j^{\fracrac{s-s_1}{n}} \|_{L^{\fracrac{n}{s_1},1}(\mathbb R^n)}
=C (1+|t|)^{\fracrac{n}{2}+1} \|\varphi_j^*(r) r^{\fracrac{s-s_1}{n}}\|_{L^{\fracrac{n}{s_1},1}(0,\infty)}\\
&=C (1+|t|)^{\fracrac{n}{2}+1} \|\varphi_j^* \|_{L^{\fracrac{n}{s},1}(0,\infty)}
= C (1+|t|)^{\fracrac{n}{2}+1} \|\varphi_j \|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}.
\end{align*}
Notice that in the previous estimate we consecutively used Lemmas~\ref{L:interpolation2} and \ref{L:interpolation} and the fact that $h_j$ is measure preserving.
Therefore,
\betagin{equation}\labelel{E:endpoint1}
|F(1+it)|\leq C (1+|t|)^{\fracrac{n}{2}+1} \sup_{j\in \mathbb Z} \|\varphi_j \|_{L^{\fracrac{n}{s},1}(\mathbb R^n)} (\|f\|_{L^{p}(\mathbb R^n)}+\varepsilon)^{\fracrac{p}{p_1}} (\|g\|_{L^{p'}(\mathbb R^n)}+\varepsilon)^{\fracrac{p'}{p_1'}}.
\end{equation}
A combination of~\eqref{E:assumption_interpolation}, \eqref{E:endpoint0}, \eqref{E:endpoint1} and Lemma~\ref{L:ThreeLines} yields
\betagin{equation}\labelel{E:theta}
|F(\theta)|\leq C\sup_{j\in \mathbb Z} \|\varphi_j \|_{L^{\fracrac{n}{s},1}(\mathbb R^n)} (\|f\|_{L^{p}(\mathbb R^n)}+\varepsilon) (\|g\|_{L^{p'}(\mathbb R^n)}+\varepsilon).
\end{equation}
Observe that for every $\xi\neq 0$,
\betagin{align*}
\sigmagma_\theta(\xi)
&=\sum_{j\in \mathbb Z} (I-\Delta)^{-\fracrac{s}{2}}[(I-\Delta)^{\fracrac{s}{2}}[\sigmagma(2^j\cdot)\widehat{\Psi}]](2^{-j}\xi) \widehat{\Phi}(2^{-j}\xi)\\
&=\sum_{j\in \mathbb Z} \sigmagma(\xi) \widehat{\Psi}(2^{-j}\xi) \widehat{\Phi}(2^{-j}\xi)
=\sum_{j\in \mathbb Z} \sigmagma(\xi) \widehat{\Psi}(2^{-j}\xi)
=\sigmagma(\xi).
\end{align*}
Thus,
$$
F(\theta) = \int_{\mathbb R^n} \sigmagma(\xi) \widehat{f_\theta^\varepsilon}(\xi) \widehat{ {g}_\theta^\varepsilon}(\xi) \, d\xi \, .
$$
Notice that
\betagin{align*}
&\bigg| \int_{\mathbb R^n} \sigmagma(\xi) \widehat{f_\theta^\varepsilon}(\xi) \widehat{ {g}_\theta^\varepsilon}(\xi) \, d\xi
- \int_{\mathbb R^n} \sigmagma(\xi) \widehat{f }(\xi) \widehat{ g }(\xi) \, d\xi \bigg| \\
= &\bigg| \int_{\mathbb R^n} \sigmagma(\xi) \Big[ \widehat{f_\theta^\varepsilon}(\xi) \big(\widehat{ {g}_\theta^\varepsilon}(\xi)-\widehat{ g }(\xi) \big)
+ \widehat{g }(\xi) \big(\widehat{ {f}_\theta^\varepsilon}(\xi)-\widehat{ f }(\xi) \big) \Big]\, d\xi \bigg| \\
\le & \|\sigma\|_{L^{\infty}(\mathbb R^n)} \Big[ \|f_\theta^\varepsilon\|_{L^2(\mathbb R^n)} \|{g}_\theta^\varepsilon -g\|_{L^2(\mathbb R^n)} +
\|g\|_{L^2(\mathbb R^n)} \|{f}_\theta^\varepsilon -f\|_{L^2(\mathbb R^n)} \Big] \\
\le & C\sup_{j\in \mathbb Z} \|(I-\Delta)^{\fracrac{s}{2}}[\widehat{\Psi}\sigma(2^j\cdot)]\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)} \Big[ \|f^\varepsilon_\theta \|_{L^2(\mathbb R^n)} \|{g}_\theta^\varepsilon -g\|_{L^2(\mathbb R^n)} +
\|g \|_{L^2(\mathbb R^n)} \|{f}_\theta^\varepsilon -f\|_{L^2(\mathbb R^n)} \Big]\, .
\end{align*}
Recall that the functions $f_0^\varepsilon$ and $g_0^\varepsilon$ were chosen in such a way that ${f}_\theta^\varepsilon -f$ and ${g}_\theta^\varepsilon -g$ converge to zero in $L^2(\mathbb R^n)$ as $\varepsilon$ converges to $0$. Therefore,
letting $\varepsilon\to 0$ in~\eqref{E:theta} yields
$$
\bigg|\int_{\mathbb R^n} \sigmagma(\xi) \widehat{f }(\xi) \widehat{ g }(\xi) \, d\xi \bigg|\le
C\, \sup_{j\in\mathbb Z}
\big\|{(I-\Deltalta)^{\fracrac{s}2}[\sigmagma(2^j\cdot)\widehat{\Psi}]}\big\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}
\norm{f}_{L^{p}(\mathbb R^n)} \|g\|_{L^{p'}(\mathbb R^n)}.
$$
Taking the supremum over all functions $g\in L^{p'}(\mathbb R^n)$ with $\| g\|_{L^{p'}(\mathbb R^n)} \le 1$ we obtain
$$
\norm{T_{\sigmagma }(f)}_{L^p(\mathbb R^n)}\le C\, \sup_{j\in\mathbb Z}
\big\|{(I-\Deltalta)^{\fracrac{s}2}[\sigmagma(2^j\cdot)\widehat{\Psi}]}\big\|_{L^{\fracrac{n}{s},1}(\mathbb R^n)}
\norm{f}_{L^{p}(\mathbb R^n)}.
$$
The proof is complete.
\end{proof}
\betagin{thebibliography}{99}
\bibitem
{BS} C. Bennett and R.Sharpley, {\it Interpolation of operators},
Academic Press, Boston, 1988.
\bibitem{CT} A. P. Calder\'on and A. Torchinsky,
{\it Parabolic maximal functions associated with a distribution, II,}
Adv. in Math. \textbf{24} (1977), 101--171.
\bibitem{CP}
A. Cianchi and L. Pick, {\it Sobolev embeddings into BMO, VMO and $L^\infty$}, Ark. Mat. {\bf 36} (1998), 317 -- 340.
\bibitem{CPS}
A. Cianchi, L. Pick and L. Slav\'{\i}kov\'a, \emph{Higher-order
Sobolev embeddings and isoperimetric inequalities}, Adv.\
Math. \textbf{273} (2015), 568--650.
\bibitem{EO}
D. E. Edmunds and B. Opic, \emph{Boundedness of fractional maximal operators between classical and weak type Lorentz spaces}, Dissertationes Math. {\bf 410} (2002), 50 pp.
\bibitem{CFA}
L. Grafakos, \emph{Classical Fourier Analysis}, 3rd edition, GTM 249, Springer-Verlag, NY 2014.
\bibitem{GraHeHonNg1} L. Grafakos, D. He, P. Honz\'\i k, and H. V. Nguyen,
\emph{The H\"ormander multiplier theorem I: The linear case revisited}, submitted, available at https://arxiv.org/pdf/1607.02620.pdf
\bibitem{hirschman} I. I. Jr. Hirschman,
\emph{A convexity theorem for certain groups of transformations},
J. Analyse Math.
\textbf{2} (1953), 209--218.
\bibitem{hirschman2} I. I. Jr. Hirschman, \emph{On multiplier transformations}, Duke Math. J. {\bf 26} (1959),
221--242.
\bibitem{Hoe} L. H\"ormander,
\emph{Estimates for translation invariant operators
in $L^p$ spaces,} Acta Math. {\bf 104} (1960), 93--139.
\bibitem{Mikhlin} S. G. Mikhlin,
\emph{On the multipliers of Fourier integrals.} (Russian)
Dokl. Akad. Nauk SSSR (N.S.) {\bf 109} (1956), 701--703.
\bibitem{Miy} A. Miyachi, \emph{On some Fourier multipliers for $H^p(\mathbb R^n)$}, J. Fac. Sci. Univ. Tokyo
Sect. IA Math. 27 (1980), 157--179.
\bibitem{MT} A. Miyachi, N. Tomita,
\emph{Minimal smoothness conditions for bilinear Fourier multipliers}, Rev. Mat. Iberoam.
{\bf 29} (2013), 495--530.
\bibitem{Seeger1} A. Seeger, \emph{A limit case of the H\"ormander multiplier theorem},
Monatsh. Math. {\bf 105} (1988), 151--160.
\bibitem{Seeger2} A. Seeger, \emph{Estimates near $L\sp 1$ for Fourier multipliers
and maximal functions}, Arch. Math. (Basel) {\bf 53} (1989), 188--193.
\bibitem{St1} E. M. Stein, {\it Singular integral and
differentiability properties of functions}, Princeton Univ. Press,
Princeton, NJ, 1970.
\bibitem{S} E. M. Stein, {\it Editor's note: The differentiability of functions in $\mathbb R^n$}, Annals of Math. {\bf 113} (1981), 383 -- 385.
\bibitem{W} S. Wainger, \emph{Special trigonometric series in k-dimensions}, Mem. Amer. Math. Soc.
{\bf 59} (1965), 1--102.
\end{thebibliography}
\iffalse
\betagin{thebibliography}{99}
\bibitem{Aguirre} J. Aguirre,
{\it Multilinear Pseudo-differential operators and paraproducts}, Thesis (Ph.D.)--Washington University in St. Louis, 1981, 155 pp.
\bibitem{AC} A. P. Calder\'on, {\it Commutators of singular
integrals}, Proc. Nat. Acad. Sci. U.S.A. {\bf 53} (1965), 1092--1099.
\bibitem{CC} C. P. Calder\'on, {\it On commutators of singular
integrals}, Studia Math. {\bf 53} (1975), 139--174.
\bibitem{CT} A. P. Calder\'on and A. Torchinsky,
{\it Parabolic maximal functions associated with a distribution, II,}
Adv. in Math. \textbf{24} (1977), 101--171.
\bibitem{CL} J. Chen and G. Lu,
{\it H\"ormander type theorems for multi-linear and
multi-parameter Fourier multiplier operators with
limited smoothness}, Nonlinear Anal. {\bf 101} (2014) 98--112.
\bibitem{CJ} M. Christ and J.-L. Journ\'e, {\it Polynomial growth estimates for multilinear singular integral
operators}, Acta Math. {\bf 159} (1987), 51--80.
\bibitem{CW} M. Christ and M. Weinstein,
{\it Dispersion of small-amplitude solutions of the generalized Korteweg-de Vries equation},
J. Funct. Anal. (1991) {\bf 100}, 87--109.
\bibitem{CMcM} R. R. Coifman, A. McIntosh and Y. Meyer,
\emph{L' int\'egrale de Cauchy d\'efinit un op\'erateur born\'e sur $L^2$ pour les courbes lipschitziennes},
Ann. of Math. (2) {\bf 116} (1982), 361--387.
\bibitem{CM1} R. R. Coifman and Y. Meyer, {\it On commutators of singular
integral and bilinear singular integrals}, Trans. Amer. Math. Soc. {\bf 212} (1975), 315--331.
\bibitem{CM-G} R. R. Coifman and Y. Meyer, {\it Commutateurs d' int\'egrales
singuli\`eres et op\'erateurs multilin\'eaires}, Ann. Inst. Fourier, Grenoble
\textbf{28} (1978), 177--202.
\bibitem{CM2} R. R. Coifman and Y. Meyer, {\it Au del\`a des op\'erateurs
pseudodiff\'erentiels}, Ast\'erisque {\bf 57} (1978).
\bibitem{DGY} X. T. Duong, L. Grafakos and L. X. Yan,
{\it Multilinear operators with non-smooth kernels and commutators of singular integrals},
Trans. Amer. Math. Soc. {\bf 362} (2010), 2089-2113.
\bibitem{FuTo} M. Fujita and N. Tomita,
\emph{Weighted norm inequalities for multilinear Fourier multipliers},
Trans. Amer. Math. Soc. \textbf{364} (2012), 6335--6353.
\bibitem{Grafakos1} L. Grafakos, {\it Classical Fourier Analysis, 3rd Edition}, GTM 249, Springer, New York, 2014.
\bibitem{GrafakosMFA} L. Grafakos, {\it Modern Fourier Analysis, 3rd Edition}, GTM 250, Springer, New York, 2014.
\bibitem{GraHeHonNg1} L. Grafakos, D. He, P. Honz\'\i k, and H. V. Nguyen,
\emph{The H\"ormander multiplier theorem I: The linear case revisited}, submitted, available at https://arxiv.org/pdf/1607.02620.pdf
\bibitem{GrNg} L. Grafakos and H. V. Nguyen, {\it
Multilinear Fourier multipliers with minimal Sobolev regularity, I}, Colloq. Math., to appear.
\bibitem{GrMiNgTo} L. Grafakos, A. Miyachi, H. V. Nguyen and N. Tomita, {\it
Multilinear Fourier multipliers with minimal Sobolev regularity, II}, submitted.
\bibitem{GrMiTo} L. Grafakos, A. Miyachi and N. Tomita, \emph{On multilinear
Fourier multipliers of limited smoothness,} Can. J.
Math. \textbf{65} (2013), 299--330.
\bibitem{GrOh} L. Grafakos and S. Oh, \emph{The Kato-Ponce inequality},
Comm. in PDE {\bf 39} (2014), 1128--1157.
\bibitem{GrSi} L. Grafakos and Z. Si, {\it The H\"ormander multiplier theorem for multilinear operators},
J. Reine Angew. Math. {\bf 668} (2012), 133--147.
\bibitem {GT2} L. Grafakos and R. H. Torres, {\it Multilinear Calder\'on-Zygmund theory},
Adv. in Math. {\bf 165} (2002), 124-164.
\bibitem{HLLW} Y. Han, J. Li, G. Lu, and P. Wang,
{\it $H^p\to H^p$ boundedness implies $H^p\to L^p$ boundedness},
Forum Math. {\bf 23} (2011), 729--756.
\bibitem{He2014}
D.~He, {\it Square function characterization of weak Hardy spaces},
Jour. Fourier Anal. Appl. {\bf 20} (2014), 1083--1110.
\bibitem{Ho} L. H\"ormander, \emph{Estimates for translation invariant operators in $L^p$ spaces},
Acta Math. \textbf{104} (1960), 93--140.
\bibitem {Jo1} J.-L. Journ\'e,
{\it Calder\'on--Zygmund operators on product spaces},
Rev.~Mat.~Iberoamericana, {\bf 1} (1985), 55--91.
\bibitem {Jo2} J.-L. Journ\'e, {\it Two problems of Calder\'on--Zygmund operators on product spaces},
Ann. Inst. Fourier, Grenoble, {\bf 38} (1988), 111--132.
\bibitem {KP} T. Kato and G. Ponce, {\it Commutator estimates and the Euler and Navier-Stokes equations},
Comm. Pure Appl. Math {\bf XLI} (1988), 891--907.
\bibitem {KS} C. E. Kenig and E. M. Stein, {\it Multilinear estimates and fractional
integration},
Math. Res. Letters, {\bf 6} (1999), 1--15.
\bibitem{Mi} S. G. Mikhlin, \emph{On the multipliers of Fourier integrals}, (Russian) Dokl. Akad. Nauk
SSSR (N.S.) \textbf{109} (1956), 701--703.
\bibitem{Miy} A. Miyachi, \emph{On some Fourier multipliers for $H^p(\mathbb R^n)$}, J. Fac. Sci. Univ. Tokyo
Sect. IA Math. 27 (1980), 157--179.
\bibitem{MT} A. Miyachi, N. Tomita,
\emph{Minimal smoothness conditions for bilinear Fourier multipliers}, Rev. Mat. Iberoam.
{\bf 29} (2013), 495--530.
\bibitem{Mu1} C. Muscalu, \emph{Calder\'on commutators and the Cauchy integral
on Lipschitz curves revisited I. First commutator and generalizations},
Rev. Mat. Iberoam. {\bf 30} (2014), 727--750.
\bibitem{Mu2} C. Muscalu, \emph{Calder\'on commutators and the Cauchy integral
on Lipschitz curves revisited II. The Cauchy
integral and its generalizations},
Rev. Mat. Iberoam. {\bf 30} (2014), 1089--1122.
\bibitem{Mu3} C. Muscalu, \emph{Calder\'on commutators and the Cauchy integral
on Lipschitz curves revisited III. Polydisc extensions},
Rev. Mat. Iberoam. {\bf 30} (2014), 1413--1437.
\bibitem{MuPiTaTh} C. Muscalu, J. Pipher, T. Tao and C. Thiele, {\it Bi-parameter paraproducts},
Acta Math. {\bf 193} (2004), 269--296.
\bibitem{MuPiTaTh2} C. Muscalu, J. Pipher, T. Tao and C. Thiele, {\it Mutli-parameter paraproducts},
Rev. Mat. Iberoamericana {\bf 22} (2006), 963--976.
\bibitem{SSS} A. Seeger, C. K. Smart, and B. Street, {\it
Multilinear singular integral forms of Christ-Journ\'e type}, preprint http://arxiv.org/abs/1510.06990
\bibitem{St2} E. M. Stein, {\it The characterization of functions arising as potentials},
Bull. Amer. Math. Soc.
{\bf 67} (1961), 102--104.
\bibitem{St1} E. M. Stein, {\it Singular integral and
differentiability properties of functions}, Princeton Univ. Press,
Princeton, NJ, 1970.
\bibitem{To} N. Tomita,
\emph{A H\"ormander type multiplier theorem for multilinear operators,} J. Funct. Anal.
\textbf{259} (2010), 2028--2044.
\bibitem{Tri} H. Triebel,
{\it Theory of function spaces II}, Monographs in Mathematics,
{\bf 84} Birkh\"auser Verlag, Basel, 1992. viii+370 pp.
\end{thebibliography}
\fraci
\end{document} | math |
What a special evening. Congrats to Crowley/Stutenroth for their victory capping an overallvictorious night for Team Fries/Greene. Well done gentlemen.
Of course the bocce tourney was just a small part of the evening. The main reason for the event was to help raise money for the Harden Family. By all accounts this too was a success. With a total tally of $77,759.53 we totally surpassed any reasonable expectations.
Terrace Park – you nailed it!
Thank you all for the unwavering support. | english |
بہٕ چھس أمس فون کٔرتھ پرژھان | kashmiri |
using System;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Collections.Generic;
using System.Security.Cryptography;
namespace RedditBet.Bot.Utils
{
using HtmlAgilityPack;
using RedditBet.Bot.Models;
using RedditBet.Bot.DataResources;
public class Comments : List<Comment>
{
public void AddComment(Comment c)
{
if (c == null) return;
if (this.Any(x => x.GetHashId() == c.GetHashId())) return;
this.Add(c);
}
}
public class Comment
{
private string _author;
private string _permaLink;
private string _hashId;
private string _message;
private int _upVotes;
private double _confidence;
public Comment(string author, string permaLink, string message, int upVotes, double confidence)
{
_author = author;
_permaLink = permaLink;
_hashId = CreateHashId(permaLink);
_message = message;
_upVotes = upVotes;
_confidence = confidence;
}
public Comment(string author, string permaLink, int upVotes)
{
_author = author;
_permaLink = permaLink;
_hashId = CreateHashId(permaLink);
_upVotes = upVotes;
}
public string GetHashId()
{
return _hashId;
}
public string GetAuthor()
{
return _author;
}
public string GetPermaLink()
{
return _permaLink;
}
public double GetConfidence()
{
return _confidence;
}
public int GetUpVotes()
{
return _upVotes;
}
public string GetMessage()
{
return _message;
}
public BotTask ToBotTask()
{
var bt = new BotTask();
var data = new TaskData();
data.Add(new TaskDataItem(Config.TargetUrl_Key, _permaLink));
data.Add(new TaskDataItem(Config.HashId_Key, _hashId));
data.Add(new TaskDataItem(Config.Message_Key, _message));
bt.TaskType = TaskType.Reply;
bt.TaskData = data;
return bt;
}
/// <summary>
/// Todo...
/// </summary>
/// <param name="permaLink">Takes the permaLink, hashes it, and then creates a string from it.</param>
/// <returns>string</returns>
private string CreateHashId(string permaLink)
{
/*
* Note: It is assumed that the permalink is guaranteed unique. This should not be used as a primary key, but given the
* temporary nature of these records it should be safe to be used as a key for quick lookups or potentially part of a temp url.
*/
return permaLink.ToHashString();
}
}
/// <summary>
/// Wrapper for RedditSharp comments (using reddit api)
/// </summary>
internal class BetBotComment : RedditSharp.Things.Comment
{
private RedditSharp.Things.Comment _comment;
public BetBotComment(RedditSharp.Things.Comment comment)
{
_comment = (RedditSharp.Things.Comment)comment.Parent;
}
public BotTask ToBotTask(TaskType type)
{
var bt = new BotTask();
var data = new TaskData();
var author = _comment.Author ?? "";
var upVotes = _comment.Upvotes.ToString() ?? "";
bt.TaskType = type;
bt.Completed = false;
data.Add(new TaskDataItem(Config.Username_Key, author));
data.Add(new TaskDataItem(Config.Upvotes_Key, upVotes));
bt.TaskData = data;
return bt;
}
}
}
| code |
/**
* Copyright 2005-2015 The Kuali Foundation
*
* Licensed under the Educational Community License, Version 2.0 (the "License");
* you may not use this file except in compliance with the License.
* You may obtain a copy of the License at
*
* http://www.opensource.org/licenses/ecl2.php
*
* Unless required by applicable law or agreed to in writing, software
* distributed under the License is distributed on an "AS IS" BASIS,
* WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
* See the License for the specific language governing permissions and
* limitations under the License.
*/
package org.kuali.rice.krad.uif.util;
import static org.junit.Assert.assertEquals;
import static org.junit.Assert.assertFalse;
import static org.junit.Assert.assertNotNull;
import static org.junit.Assert.assertNull;
import static org.junit.Assert.assertSame;
import static org.junit.Assert.assertTrue;
import static org.junit.Assert.fail;
import java.beans.BeanInfo;
import java.beans.IntrospectionException;
import java.beans.Introspector;
import java.beans.PropertyDescriptor;
import java.beans.PropertyEditorSupport;
import java.io.Serializable;
import java.lang.annotation.Retention;
import java.lang.annotation.RetentionPolicy;
import java.lang.reflect.Method;
import java.math.BigDecimal;
import java.sql.Timestamp;
import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
import java.util.List;
import java.util.Map;
import org.junit.AfterClass;
import org.junit.BeforeClass;
import org.junit.Test;
import org.kuali.rice.core.api.CoreConstants;
import org.kuali.rice.core.api.config.property.ConfigContext;
import org.kuali.rice.core.api.resourceloader.GlobalResourceLoader;
import org.kuali.rice.core.api.util.type.KualiDecimal;
import org.kuali.rice.core.api.util.type.KualiPercent;
import org.kuali.rice.krad.service.KRADServiceLocatorWeb;
import org.kuali.rice.krad.uif.UifConstants;
import org.kuali.rice.krad.uif.UifParameters;
import org.kuali.rice.krad.uif.component.BindingInfo;
import org.kuali.rice.krad.uif.container.CollectionGroup;
import org.kuali.rice.krad.uif.container.CollectionGroupBase;
import org.kuali.rice.krad.uif.container.CollectionGroupBuilder;
import org.kuali.rice.krad.uif.container.Group;
import org.kuali.rice.krad.uif.container.GroupBase;
import org.kuali.rice.krad.uif.element.Action;
import org.kuali.rice.krad.uif.element.Message;
import org.kuali.rice.krad.uif.element.ViewHeader;
import org.kuali.rice.krad.uif.layout.StackedLayoutManager;
import org.kuali.rice.krad.uif.layout.StackedLayoutManagerBase;
import org.kuali.rice.krad.uif.lifecycle.ViewLifecycle;
import org.kuali.rice.krad.uif.service.impl.ViewHelperServiceImpl;
import org.kuali.rice.krad.uif.view.FormView;
import org.kuali.rice.krad.uif.view.ViewPresentationControllerBase;
import org.kuali.rice.krad.util.GlobalVariables;
import org.kuali.rice.krad.util.KRADConstants;
import org.kuali.rice.krad.web.bind.RequestAccessible;
import org.kuali.rice.krad.web.bind.UifConfigurableWebBindingInitializer;
import org.kuali.rice.krad.web.bind.UifServletRequestDataBinder;
import org.kuali.rice.krad.web.form.UifFormBase;
import org.slf4j.Logger;
import org.slf4j.LoggerFactory;
import org.springframework.mock.web.MockHttpServletRequest;
import org.springframework.web.context.request.RequestContextHolder;
import org.springframework.web.context.request.ServletRequestAttributes;
import org.springframework.web.context.request.ServletWebRequest;
import org.springframework.web.servlet.ModelAndView;
public class ObjectPropertyUtilsTest extends ProcessLoggingUnitTest {
final Logger LOG = LoggerFactory.getLogger(ObjectPropertyUtilsTest.class);
@Retention(RetentionPolicy.RUNTIME)
public @interface TestAnnotation {
String afoo();
}
@BeforeClass
public static void setup() throws Exception {
UifUnitTestUtils.establishMockConfig("ObjectPropertyUtilsTest");
}
@AfterClass
public static void teardown() throws Exception {
UifUnitTestUtils.tearDownMockConfig();
}
public static class TestBean implements Serializable {
private static final long serialVersionUID = 1L;
public TestBean() {}
@RequestAccessible
private String rwProp;
private TestBeanTwo complexProp;
public String getRwProp() {
return this.rwProp;
}
public void setRwProp(String r) {
this.rwProp = r;
}
private String woProp;
public void setWoProp(String w) {
this.woProp = w;
}
private String roProp;
@TestAnnotation(afoo = "abar")
public String getRoProp() {
return this.roProp;
}
private Boolean bitProp;
public boolean isBitProp() {
return bitProp != null && bitProp;
}
public Boolean getBitProp() {
return bitProp;
}
public void setBitProp(Boolean bitProp) {
this.bitProp = bitProp;
}
private boolean booleanProp;
public boolean isBooleanProp() {
return booleanProp;
}
public void setBooleanProp(boolean booleanProp) {
this.booleanProp = booleanProp;
}
private Timestamp timestampProp;
public Timestamp getTimestampProp() {
return timestampProp;
}
public void setTimestampProp(Timestamp timestampProp) {
this.timestampProp = timestampProp;
}
private Date dateProp;
public Date getDateProp() {
return dateProp;
}
public void setDateProp(Date dateProp) {
this.dateProp = dateProp;
}
private int intProp;
public int getIntProp() {
return intProp;
}
private BigDecimal bigDecimalProp;
public BigDecimal getBigDecimalProp() {
return bigDecimalProp;
}
public void setBigDecimalProp(BigDecimal bigDecimalProp) {
this.bigDecimalProp = bigDecimalProp;
}
public void setIntProp(int intProp) {
this.intProp = intProp;
}
private Integer integerProp;
public Integer getIntegerProp() {
return integerProp;
}
public void setIntegerProp(Integer integerProp) {
this.integerProp = integerProp;
}
private TestBean next;
public TestBean getNext() {
return next;
}
public void setNext(TestBean next) {
this.next = next;
}
private List<String> stuffs;
public List<String> getStuffs() {
return stuffs;
}
public void setStuffs(List<String> stuffs) {
this.stuffs = stuffs;
}
private Object[] arrayProp;
public Object[] getArrayProp() {
return arrayProp;
}
public void setArrayProp(Object[] arrayProp) {
this.arrayProp = arrayProp;
}
private Map<String, Object> mapProp;
public Map<String, Object> getMapProp() {
return this.mapProp;
}
public void setMapProp(Map<String, Object> mapProp) {
this.mapProp = mapProp;
}
/**
* @return the complexProp
*/
public TestBeanTwo getComplexProp() {
return this.complexProp;
}
/**
* @param complexProp the complexProp to set
*/
public void setComplexProp(TestBeanTwo complexProp) {
this.complexProp = complexProp;
}
}
public static class TestBeanTwo {
private String fooProp;
/**
* @return the fooProp
*/
public String getFooProp() {
return this.fooProp;
}
/**
* @param fooProp the fooProp to set
*/
public void setFooProp(String fooProp) {
this.fooProp = fooProp;
}
}
@Test
public void testSetBoolean() {
TestBean tb = new TestBean();
ObjectPropertyUtils.setPropertyValue(tb, "booleanProp", "true");
assertTrue(tb.isBooleanProp());
}
@Test
public void testGetPropertyDescriptor() {
Map<String, PropertyDescriptor> pds = ObjectPropertyUtils.getPropertyDescriptors(TestBean.class);
assertNotNull(pds.get("rwProp"));
assertNotNull(pds.get("roProp"));
assertNotNull(pds.get("woProp"));
assertNull(pds.get("foobar"));
}
@Test
public void testGet() {
TestBean tb = new TestBean();
tb.setRwProp("foobar");
assertEquals("foobar", ObjectPropertyUtils.getPropertyValue(tb, "rwProp"));
tb.roProp = "barbaz";
assertEquals("barbaz", ObjectPropertyUtils.getPropertyValue(tb, "roProp"));
try {
ObjectPropertyUtils.getPropertyValue(tb, "woProp");
// KULRICE-10677 - should return null - fail("expected exception");
} catch (RuntimeException e) {
// KULRICE-10677 - should return null
throw e;
}
}
@Test
public void testLookup() {
TestBean tb = new TestBean();
tb.roProp = "barbaz";
assertEquals("barbaz", ObjectPropertyUtils.getPropertyValue(tb, "roProp"));
Map<String, Object> tm = new java.util.HashMap<String, Object>();
tb.setMapProp(tm);
tm.put("barbaz", "hooray!");
tm.put("bar.baz", "hoorah!");
tm.put("bar.[baz]", "foobah!");
tm.put("b'('r.[\"ain)\"s]", "zombie!");
assertEquals("hooray!", ObjectPropertyUtils.getPropertyValue(tb, "mapProp[barbaz]"));
assertEquals("hooray!", ObjectPropertyUtils.getPropertyValue(tb, "mapProp['barbaz']"));
assertEquals("hooray!", ObjectPropertyUtils.getPropertyValue(tb, "mapProp[\"barbaz\"]"));
assertEquals("hoorah!", ObjectPropertyUtils.getPropertyValue(tb, "mapProp[bar.baz]"));
assertEquals("foobah!", ObjectPropertyUtils.getPropertyValue(tb, "mapProp[bar.[baz]]"));
assertEquals("zombie!", ObjectPropertyUtils.getPropertyValue(tb, "mapProp['b'('r.[\"ain)\"s]']"));
assertEquals("zombie!", ObjectPropertyUtils.getPropertyValue(tb, "mapProp[b'('r.[\"ain)\"s]]"));
TestBean tb2 = new TestBean();
tb2.setRwProp("foodbar");
tb.setNext(tb2);
tm.put("blah", new Object[]{"next", "rwProp"});
tm.put("baz", tb2);
assertTrue(ObjectPropertyUtils.isReadableProperty(tb, "mapProp[\"baz\"].rwProp"));
assertEquals("barbaz", ObjectPropertyUtils.getPropertyValue(tb, "roProp"));
assertEquals("foodbar", ObjectPropertyUtils.getPropertyValue(tb, "next.rwProp"));
tb.setStuffs(Arrays.asList(new String[]{"foo", "bar", "baz",}));
assertEquals("bar", ObjectPropertyUtils.getPropertyValue(tb, "stuffs[1]"));
TestBean rb = new TestBean();
TestBean nb = new TestBean();
TestBean lb = new TestBean();
rb.setNext(nb);
nb.setNext(lb);
assertEquals(String.class, ObjectPropertyUtils.getPropertyType(rb, "next.next.rwProp"));
rb.setRwProp("baz");
nb.setRwProp("bar");
lb.setRwProp("foo");
assertEquals("foo", ObjectPropertyUtils.getPropertyValue(rb, "next.next.rwProp"));
}
@Test
public void testSet() throws Throwable {
TestBean tb = new TestBean();
ObjectPropertyUtils.setPropertyValue(tb, "rwProp", "foobar");
assertEquals("foobar", tb.getRwProp());
ObjectPropertyUtils.setPropertyValue(tb, "woProp", "barbaz");
assertEquals("barbaz", tb.woProp);
try {
ObjectPropertyUtils.setPropertyValue(tb, "roProp", "bazfoo");
fail("expected exception");
} catch (Exception E) {
// OK!
}
long now = System.currentTimeMillis();
ObjectPropertyUtils.setPropertyValue(tb, "dateProp", new java.sql.Date(now));
assertEquals(now, tb.getDateProp().getTime());
String dateStr = "01/03/2013";
ObjectPropertyUtils.setPropertyValue(tb, "dateProp", dateStr);
Date expectedDate = new SimpleDateFormat("MM/dd/yy").parse(dateStr);
assertEquals(expectedDate, tb.getDateProp());
}
@Test
public void testGetAsText() throws Throwable {
String dateStr = "01/03/2013";
Date expectedDate = new SimpleDateFormat("MM/dd/yy").parse(dateStr);
TestBean tb = new TestBean();
tb.setDateProp(expectedDate);
assertEquals("01/03/13", ObjectPropertyUtils.getPropertyValueAsText(tb, "dateProp"));
}
public static class TestForm extends UifFormBase {
private static final long serialVersionUID = 6597388705374534394L;
private TestBean bean;
/**
* @return the bean
*/
public TestBean getBean() {
return this.bean;
}
/**
* @param bean the bean to set
*/
public void setBean(TestBean bean) {
this.bean = bean;
}
}
public static class FooEditor extends PropertyEditorSupport {
@Override
public String getAsText() {
return "foobar";
}
}
// TODO: Move to integration test
// @Test
// public void testCustomEditor() throws Throwable {
// TestForm form = new TestForm();
// MockHttpServletRequest request = new MockHttpServletRequest();
// request.setParameter(UifParameters.VIEW_ID, "TestViewWithPropertyEditor");
// request.setParameter("bean.next.rwProp", "not foobar");
// RequestContextHolder.setRequestAttributes(new ServletRequestAttributes(request));
// UifServletRequestDataBinder binder = new UifServletRequestDataBinder(form);
// new UifConfigurableWebBindingInitializer().initBinder(binder, new ServletWebRequest(request));
// binder.bind(request);
//
// ModelAndView modelAndView = new ModelAndView();
// modelAndView.addObject(UifConstants.DEFAULT_MODEL_NAME, form);
//
// KRADServiceLocatorWeb.getModelAndViewService().prepareView(request, modelAndView);
// assertEquals("foobar", ObjectPropertyUtils.getPropertyValueAsText(form, "bean.next.rwProp"));
// }
@Test
public void testPathSet() {
TestBean tb = new TestBean();
ObjectPropertyUtils.setPropertyValue(tb, "rwProp", "bar");
assertEquals("bar", tb.getRwProp());
ObjectPropertyUtils.setPropertyValue(tb, "next", new TestBean());
ObjectPropertyUtils.setPropertyValue(tb, "next.next", new TestBean());
ObjectPropertyUtils.setPropertyValue(tb, "next.next.woProp", "baz");
assertEquals("baz", tb.getNext().getNext().woProp);
}
@Test
public void testBulk() {
Map<String, String> pd = new java.util.HashMap<String, String>();
pd.put("rwProp", "foobar");
pd.put("intProp", "3");
pd.put("booleanProp", "true");
pd.put("stuffs", "foo,bar,baz");
for (int i = 0; i < 10000; i++) {
TestBean tb = new TestBean();
ObjectPropertyUtils.copyPropertiesToObject(pd, tb);
assertEquals("foobar", tb.getRwProp());
assertEquals(3, tb.getIntProp());
assertEquals(true, tb.isBooleanProp());
assertEquals(3, tb.getStuffs().size());
assertEquals("foo", tb.getStuffs().get(0));
assertEquals("bar", tb.getStuffs().get(1));
assertEquals("baz", tb.getStuffs().get(2));
}
}
@Test
public void testReadWriteCheck() {
TestBean tb = new TestBean();
assertTrue(ObjectPropertyUtils.isReadableProperty(tb, "rwProp"));
assertTrue(ObjectPropertyUtils.isWritableProperty(tb, "rwProp"));
assertTrue(ObjectPropertyUtils.isReadableProperty(tb, "roProp"));
assertFalse(ObjectPropertyUtils.isWritableProperty(tb, "roProp"));
assertFalse(ObjectPropertyUtils.isReadableProperty(tb, "woProp"));
assertTrue(ObjectPropertyUtils.isWritableProperty(tb, "woProp"));
}
@Test
public void testKradUifTemplateHeaderMetadata() {
FormView formView = new FormView();
ViewHeader viewHeader = new ViewHeader();
formView.setHeader(viewHeader);
Message headerMetadataMessage = new Message();
viewHeader.setMetadataMessage(headerMetadataMessage);
assertSame(headerMetadataMessage, ObjectPropertyUtils.getPropertyValue(formView, "header.metadataMessage"));
}
/**
* Collection list item type, for testing UIF interaction with ObjectPropertyUtils.
*/
public static class CollectionTestItem {
/**
* A string property, called foobar.
*/
String foobar;
/**
* @return the foobar
*/
public String getFoobar() {
return this.foobar;
}
/**
* @param foobar the foobar to set
*/
public void setFoobar(String foobar) {
this.foobar = foobar;
}
}
/**
* Reference to a collection, for testing UIF interaction with ObjectPropertyUtils.
*/
public static class CollectionTestListRef {
/**
* The collection.
*/
List<CollectionTestItem> bar;
/**
* Mapping of new line items.
*/
Map<String, CollectionTestItem> baz;
/**
* @return the bar
*/
public List<CollectionTestItem> getBar() {
return this.bar;
}
/**
* @param bar the bar to set
*/
public void setBar(List<CollectionTestItem> bar) {
this.bar = bar;
}
/**
* @return the baz
*/
public Map<String, CollectionTestItem> getBaz() {
return this.baz;
}
/**
* @param baz the baz to set
*/
public void setBaz(Map<String, CollectionTestItem> baz) {
this.baz = baz;
}
}
/**
* Mock collection form for UIF interaction with ObjectPropertyUtils.
*/
public static class CollectionTestForm extends UifFormBase {
private static final long serialVersionUID = 1798800132492441253L;
/**
* Reference to a data object that has a collection.
*/
CollectionTestListRef foo;
/**
* @return the foo
*/
public CollectionTestListRef getFoo() {
return this.foo;
}
/**
* @param foo the foo to set
*/
public void setFoo(CollectionTestListRef foo) {
this.foo = foo;
}
}
@Test
public void testKradUifCollectionGroupBuilder() throws Throwable {
UifUnitTestUtils.establishMockConfig(ObjectPropertyUtilsTest.class.getSimpleName());
UifUnitTestUtils.establishMockUserSession("testuser");
try {
// Performance medium generates this property path:
// newCollectionLines['newCollectionLines_'mediumCollection1'_.subList']
// Below recreates the stack trace that ensued due to poorly escaped quotes,
// and proves that the parser works around bad quoting in a manner similar to BeanWrapper
final CollectionGroupBuilder collectionGroupBuilder = new CollectionGroupBuilder();
final CollectionTestForm form = new CollectionTestForm();
CollectionTestItem item = new CollectionTestItem();
item.setFoobar("barfoo");
ObjectPropertyUtils.setPropertyValue(form, "foo.baz['foo_bar_'badquotes'_.foobar']", item);
assertEquals("barfoo", form.foo.baz.get("foo_bar_'badquotes'_.foobar").foobar);
final FormView view = new FormView();
view.setFormClass(CollectionTestForm.class);
view.setViewHelperService(new ViewHelperServiceImpl());
view.setPresentationController(new ViewPresentationControllerBase());
view.setAuthorizer(UifUnitTestUtils.getAllowMostViewAuthorizer());
final CollectionGroup collectionGroup = new CollectionGroupBase();
collectionGroup.setCollectionObjectClass(CollectionTestItem.class);
collectionGroup.setAddLinePropertyName("addLineFoo");
StackedLayoutManager layoutManager = new StackedLayoutManagerBase();
Group lineGroupPrototype = new GroupBase();
layoutManager.setLineGroupPrototype(lineGroupPrototype);
collectionGroup.setLayoutManager(layoutManager);
BindingInfo addLineBindingInfo = new BindingInfo();
addLineBindingInfo.setBindingPath("foo.baz['foo_bar_'badquotes'_.foobar']");
collectionGroup.setAddLineBindingInfo(addLineBindingInfo);
BindingInfo collectionBindingInfo = new BindingInfo();
collectionBindingInfo.setBindingPath("foo.bar");
collectionGroup.setBindingInfo(collectionBindingInfo);
ViewLifecycle.encapsulateLifecycle(view, form, null, new Runnable() {
@Override
public void run() {
collectionGroupBuilder.build(view, form, (CollectionGroup) CopyUtils.copy(collectionGroup));
}
});
} finally {
GlobalVariables.setUserSession(null);
GlobalVariables.clear();
GlobalResourceLoader.stop();
}
}
@Test
public void testSetStringMapFromInt() {
Action action = new Action();
ObjectPropertyUtils.setPropertyValue(action, "actionParameters['lineIndex']", 34);
assertEquals("34", action.getActionParameter("lineIndex"));
}
@Test
public void testClassNavigation() {
assertEquals(String.class, ObjectPropertyUtils.getPropertyType(TestBean.class, "complexProp.fooProp"));
try {
// valid first reference, invalid second reference
assertEquals(null, ObjectPropertyUtils.getPropertyType(TestBean.class, "complexProp.foobar"));
// NULL is ok - fail("KULRICE-10677 - is this ok?");
} catch (IllegalArgumentException e) {
// IAE is not ok - KULRICE-10677 is this ok?
throw e;
}
try {
// invalid single reference
assertEquals(null, ObjectPropertyUtils.getPropertyType(TestBean.class, "foo"));
// NULL is ok - fail("KULRICE-10677 - is this ok?");
} catch (IllegalArgumentException e) {
// IAE is not ok - KULRICE-10677 is this ok?
throw e;
}
try {
// invalid first reference
assertEquals(null, ObjectPropertyUtils.getPropertyType(TestBean.class, "foo.bar"));
// NULL is ok - fail("KULRICE-10677 - is this ok?");
} catch (IllegalArgumentException e) {
// IAE is not ok - KULRICE-10677 is this ok?
throw e;
}
}
@Test
public void testPropertySplitPath() {
String path = "foo.foo1.foo2";
String[] splitPaths = ObjectPropertyUtils.splitPropertyPath(path);
assertEquals(3, splitPaths.length);
assertEquals("foo", splitPaths[0]);
assertEquals("foo1", splitPaths[1]);
assertEquals("foo2", splitPaths[2]);
path = "foo[1]";
splitPaths = ObjectPropertyUtils.splitPropertyPath(path);
assertEquals(1, splitPaths.length);
assertEquals("foo[1]", splitPaths[0]);
path = "foo.foo1['key.nested'].foo2";
splitPaths = ObjectPropertyUtils.splitPropertyPath(path);
assertEquals(3, splitPaths.length);
assertEquals("foo", splitPaths[0]);
assertEquals("foo1['key.nested']", splitPaths[1]);
assertEquals("foo2", splitPaths[2]);
path = "foo.foo1['key.nested'].foo2.foo3['key.nest.nest'].foo4";
splitPaths = ObjectPropertyUtils.splitPropertyPath(path);
assertEquals(5, splitPaths.length);
assertEquals("foo", splitPaths[0]);
assertEquals("foo1['key.nested']", splitPaths[1]);
assertEquals("foo2", splitPaths[2]);
assertEquals("foo3['key.nest.nest']", splitPaths[3]);
assertEquals("foo4", splitPaths[4]);
}
@Test
public void testCanonicalPath() {
String path = "foo.foo1.foo2";
assertEquals(path, ObjectPropertyUtils.getCanonicalPath(path));
path = "foo[1]";
assertEquals("foo", ObjectPropertyUtils.getCanonicalPath(path));
path = "foo.foo1['key.nested'].foo2";
assertEquals("foo.foo1.foo2", ObjectPropertyUtils.getCanonicalPath(path));
path = "foo.foo1['key.nested'].foo2.foo3['key.nest.nest'].foo4";
assertEquals("foo.foo1.foo2.foo3.foo4", ObjectPropertyUtils.getCanonicalPath(path));
}
// Classes used by testGetterInInterfaceOrSuperHasWiderType to check covariant return types on JDK6
// Holds an abstract class that is extended by Integer
public interface NumberHolder {
Number getNumber();
}
public class NumberedImplOne implements NumberHolder {
@Override
public Integer getNumber() {
return 1;
}
}
public abstract class AbstractNumberHolder implements NumberHolder {
@Override
public abstract Number getNumber();
}
public class ConcreteNumberHolder extends AbstractNumberHolder {
@Override
public Number getNumber() {
return 1;
}
}
public class ConcreteNarrowedNumberHolder extends ConcreteNumberHolder {
@Override
public Integer getNumber() {
return 1;
}
}
public class ConcreteNarrowedNumberHolderSub extends ConcreteNarrowedNumberHolder {
}
// Holds an interface that is implemented by Integer
public interface ComparableHolder {
Comparable<?> getComparable();
}
public class ComparableHolderImpl implements ComparableHolder {
@Override
public Integer getComparable() {
return 1;
}
}
// Holds a concrete superclass of KualiPercent
public interface KualiDecimalHolder {
KualiDecimal getDecimal();
}
public class KualiPercentHolder implements KualiDecimalHolder {
@Override
public KualiPercent getDecimal() {
return new KualiPercent(1d);
}
}
public class Base {
public Number getValue() { return null; }
}
public class Int extends Base {
public Integer getValue() { return Integer.valueOf(1); }
}
/**
* Verifies (at least when run on Linux in JDK6) our fix for the JDK6 Introspector
* bug/shortcoming WRT covariant return types that results in a wider getter method being
* preferred over a more specific implementation getter method.
*
* <p>
* This makes the type reported by Introspector for read methods depending on the order of
* Methods depend on the order that they are returned by reflection on a class, which has been
* demonstrated to vary between platforms.
* </p>
*/
@Test
public void testGetterInInterfaceOrSuperHasWiderType() {
Method readMethod = null;
readMethod = ObjectPropertyUtils.getReadMethod(ComparableHolderImpl.class, "comparable");
//System.out.println(readMethod.getReturnType());
assertEquals(Integer.class, readMethod.getReturnType());
readMethod = ObjectPropertyUtils.getReadMethod(NumberedImplOne.class, "number");
//System.out.println(readMethod.getReturnType());
assertEquals(Integer.class, readMethod.getReturnType());
readMethod = ObjectPropertyUtils.getReadMethod(ConcreteNarrowedNumberHolder.class, "number");
//System.out.println(readMethod.getReturnType());
assertEquals(Integer.class, readMethod.getReturnType());
readMethod = ObjectPropertyUtils.getReadMethod(ConcreteNarrowedNumberHolderSub.class, "number");
//System.out.println(readMethod.getReturnType());
assertEquals(Integer.class, readMethod.getReturnType());
// This case is *not* covered by our workaround, and would fail w/ JDK 6 on Linux if enabled.
// The interface has a concrete superclass, which will be returned in JDK6 on Linux where the
// Method order returned by reflection on a class is different, and the Introspector isn't smart
// enough to ask which Method return type is more specific.
for (int i = 0; i < 1; ++i) {
readMethod = ObjectPropertyUtils.getReadMethod(KualiPercentHolder.class, "decimal");
//System.out.println(readMethod.getReturnType());
//System.out.println(readMethod.getReturnType() == KualiDecimal.class);
}
if (readMethod.getReturnType() == KualiDecimal.class) {
LOG.info("I bet you're using JDK6 on Linux");
}
//System.out.println("==============================================");
//System.out.println("ObjectPropertyUtils.getReadMethod(Base.class, \"value\")");
readMethod = ObjectPropertyUtils.getReadMethod(Base.class, "value");
//System.out.println(readMethod.getReturnType());
assertEquals(Number.class, readMethod.getReturnType());
//System.out.println("==============================================");
//System.out.println("ObjectPropertyUtils.getReadMethod(Int.class, \"value\")");
readMethod = ObjectPropertyUtils.getReadMethod(Int.class, "value");
//System.out.println(readMethod.getReturnType());
assertEquals(Integer.class, readMethod.getReturnType());
// System.out.println("==============================================");
// try {
// // lookup bean info for given class
// BeanInfo info = Introspector.getBeanInfo(Int.class);
// if (info != null) {
// // get list of descriptors and iterate to validate each property
// PropertyDescriptor[] descriptors = info.getPropertyDescriptors();
// for (int i = 0; i < descriptors.length; i++) {
// System.out.println("--------------------------");
// PropertyDescriptor descriptor = descriptors [i];
// System.out.println(descriptor.getName());
//
// // check if read method is bridge and lookup real method
// readMethod = descriptor.getReadMethod();
// System.out.println(readMethod.getReturnType());
// System.out.println("readMethod.isBridge()=>" + readMethod.isBridge());
// if (readMethod != null && readMethod.isBridge()) {
// Method method = Int.class.getMethod(readMethod.getName(), readMethod.getParameterTypes());
// System.out.println(method.getReturnType());
//
// // if method found, update read method
// // which also updates property type
// if (method != null) {
// descriptor.setReadMethod(method);
//
// // TODO: lookup write method with same type in case the write
// // method is the bridge method
// }
// }
// }
// }
// } catch (IntrospectionException e) {
// e.printStackTrace(); //To change body of catch statement use File | Settings | File Templates.
// } catch (NoSuchMethodException e) {
// e.printStackTrace(); //To change body of catch statement use File | Settings | File Templates.
// }
// Other cases to test if we have to refine this functionality:
// * similar to the ConcreteNarrowedNumberHolder,
// but creating an abstract impl of AbstractKualiDecimalHolder as the intermediate class
// * similar to ConcreteNarrowedNumberHolderSub, but ConcreteNarrowedKualiDecimalHolderSub
}
}
| code |
Pioneers in the industry, we offer cp plus video door phone, dahua video door phone, cp jav k40 video door phone and oem video door phone from India.
We are offering our valued clients with a supreme quality range of CP Plus Video Door Phone. This product is designed and manufactured using superior quality components with the help of sophisticated technology. Also, this product is precisely checked on several quality parameters to make certain its trouble free functioning. Our clients can avail this product from us in various specifications at the most competitive price.
We have carved out a sophisticated niche among topmost organizations, betrothed in offering a high quality range of Dahua Video Door Phone. This product is manufactured by our experts using high quality components and high-end technology as per the international quality standards. Checked on several quality parameters by our quality experts, this product is provided in various technical specifications at very nominal price to the clients.
Owing to our immense domain expertise, we are offering our clients with a superior quality assortment of CP JAV K40 Video Door Phone. This product is designed and manufactured in accordance with the international quality standards using the finest quality material and state-of-the-art technology. The offered product is available in different technical specifications to meet diverse requirements of clients. Further, this product is offered at very affordable price to the clients.
Owing to our expertise in this domain, we are offering our clients with a superior quality range of OEM Video Door Phone. This OEM Video Door Phone is manufactured using excellent quality material with the help of cutting-edge technology in line with international quality standards. The offered OEM Video Door Phone is available in different specifications as per the requirements of clients. We offer this OEM Video Door Phone at the most affordable price to the clients. | english |
\begin{document}
\title[quasiconformal mappings and a Bernstein type theorem]{quasiconformal mappings and a Bernstein type theorem over exterior domains in $\mathbb{R}^2$}
\author{Dongsheng Li}
\author{Rulin Liu}
\begin{abstract}
We establish the H\"{o}lder estimate and the asymptotic behavior at infinity
for $K$-quasiconformal mappings over exterior domains in $\mathbb{R}^2$.
As a consequence, we prove an exterior Bernstein type theorem for fully nonlinear uniformly elliptic equations of second order in $\mathbb{R}^2$.
\end{abstract}
\footnotetext{\textit{Key words and phrases.} Quasiconformal Mappings, Exterior Bernstein Type Theorem, Fully Nonlinear Elliptic Equations, Asymptotic Behavior.\newline}
\footnotetext{This research is supported by NSFC 12071365.\newline}
\footnotetext{Dongsheng Li\newline
lidsh@mail.xjtu.edu.cn\newline
School of Mathematics and Statistics, Xi'an Jiaotong University, Xi'an, P.R.China 710049.\newline}
\footnotetext{Rulin Liu\newline
lrl001@stu.xjtu.edu.cn\newline
School of Mathematics and Statistics, Xi'an Jiaotong University, Xi'an, P.R.China 710049.}
\maketitle
\section{Introduction}
\indent For Bernstein type theorems for fully nonlinear elliptic equations, a famous theorem of J\"{o}rgens \cite{JO} asserts that any solution of the Monge-Amp\`{e}re equation
\begin{equation}
\label{eq:M-A}
\mbox{det}{D^2u}=1
\end{equation}
in $\mathbb{R}^2$ is a quadratic polynomial. This result was proved to be valid in higher dimensions by Calabi ($n\leq 5$ \cite{CA}) and Pogolove ($n\geq 2$ \cite{PO}) for convex $u$. The extension to the classical theorem of J\"{o}rgens, Calabi and Pogorelov above follows. In 2003, Caffarelli and Li\cite{C-LI} proved that for $n\geq 3$, any convex viscosity solution of the Monge-Amp\`{e}re equation (\ref{eq:M-A}) outside a bounded open subset of $\mathbb{R}^n$ approaches a quadratic polynomial near infinity and for $n=2$, any viscosity solution tends to a quadratic polynomial plus a logarithm term, where for the later case, Ferrer, Mart\'{i}nez and Mil\'{a}n \cite{F-F-M} obtained the same result in 1999. For the case of half space $\mathbb{R}^n_+$, Savin \cite{SA} established the Bernstein type theorem for equation (\ref{eq:M-A}) in 2014, and later, in 2020, Jia, Li and Li\cite{JIA-LI-LI} extended this theorem to exterior domains in half space.\newline
\indent By the virtue of the Evans-Krylov estimate, we can see that for $n\geq3$, any smooth entire solution of the general fully nonlinear elliptic equation
\begin{eqnarray}
\label{eq:F(D^2u)}
F\left(D^2u(x)\right)=0
\end{eqnarray}
in $\mathbb{R}^n$ is a quadratic polynomial if we assume the concavity of $F$ and the boundedness of the Hessian $D^2u$. For $n=2$, the same conclusion follows from the Nirenberg estimate \cite{NI} and the boundedness of $D^2u$ without the concavity of $F$.\newline
\indent In 2020, Li, Li and Yuan\cite{LI-LI-Y} established a higher dimensional exterior Bernstein type theorem for the fully nonlinear elliptic equation (\ref{eq:F(D^2u)}), namely, for $n\geq 3$, the solution of (\ref{eq:F(D^2u)}) in $\mathbb{R}^n\setminus\bar{B}_1(0)$ tends to a quadratic polynomial as $|x|\to\infty$ if $F$ is convex (or concave or the level set of $F$ is convex) and $D^2u$ is bounded. As applications of this theorem, the authors obtained the exterior Bernstein type theorems of Monge-Amp\`{e}re equations, special Lagrangian equations, quadratic Hessian equations and inverse harmonic Hessian equations for $n\geq 3$. As for $n=2$, the authors studied these three specific equations one by one to obtain the corresponding exterior Bernstein type theorem instead of establishing the general theorem to equation (\ref{eq:F(D^2u)}). Indeed, the method in \cite{LI-LI-Y} does not work for two dimensional problems. Roughly speaking, there are two steps in \cite{LI-LI-Y} to establish the exterior Bernstein type theorem.
First, by the concavity of $F$ and the boundedness of $D^2u$, the authors made use of the Evans-Krylov estimate and the weak Harnack inequality to show the existence of the limit $A$ of $D^2u$ at infinity, which actually holds for all $n\geq 2$. Second, it is crucial to get the decay rate of $|D^2u-A|$ as $|x|\rightarrow\infty$. This can be done by using barrier functions as $n\geq 3$ while unfortunately, such barrier does not exist as $n=2$.
\newline
\indent In this paper, we establish the exterior Bernstein type theorem for fully nonlinear elliptic equation (\ref{eq:F(D^2u)}) in $\mathbb{R}^2$ by using $K$-quasiconformal mappings. The main result goes as the following.
\begin{thm}
\label{thm:1}
Let $u$ be a viscosity solution of (\ref{eq:F(D^2u)}) in the exterior domain
$\mathbb{R}^2\setminus \bar{\Omega}$, where $F\in C^{1,1}$ is a fully nonlinear uniformly elliptic operator with ellipticity constants $\lambda$ and $\Lambda$, and $\Omega$ is a bounded domain of $\mathbb{R}^2$. If
$\left\| D^2u\right\|_{L^{\infty}(\mathbb{R}^2\setminus \bar{\Omega})}\leq M< +\infty$,
then there exists a unique symmetric matrix $A\in \mathbb{R}^{2\times 2}$, $b,e\in \mathbb{R}^2, c,d\in\mathbb{R}$
such that for any $0<\alpha<1$,
$$u(x)=\frac 12 x^{\mathrm{T}}Ax+b\cdot x+d\log{|x|}+c+e\frac{x}{|x|^2}+O\left(|x|^{-1-\alpha}\right)\text{~as~}|x|\to\infty,$$
where
\begin{equation}
\label{value of d}
d=\frac {1}{2\pi}\left(\int\limits_{\partial\Omega} u_{\nu}\mathrm{d}s+\iint\limits_{\mathbb{R}^2\setminus\bar{\Omega}} (\Delta u(x)-\mathrm{tr}A)\mathrm{d}x_1\mathrm{d}x_2-\mathrm{tr}A|\Omega|\right),
\end{equation}
$\nu$ is the unit outward normal of the boundary $\partial\Omega$.
Furthermore, if $F$ is smooth, then we have
$$\left|D^k\left(u(x)-\frac 12 x^{\mathrm{T}}Ax-b\cdot x-d\log{|x|}-c-e\frac{x}{|x|^2}\right)\right|=O\left(|x|^{-1-\alpha-k}\right)\text{~as~}|x|\to\infty$$
for all $k\in\mathbb{N}$.
\end{thm}
\begin{re}
In Theorem \ref{thm:1}, the concavity (or convexity or convexity of the level set $\{N|F(N)=0\}$) of $F$ is not needed that is however an essential assumption in \cite{LI-LI-Y}.
\end{re}
As aforementioned, we will use $K$-quasiconformal mappings to study equation (\ref{eq:F(D^2u)}) over exterior domains. $K$-quasiconformal mappings play a special role in studying the H\"{o}lder continuity of solutions of two dimensional second order partial differential equations, which was developed by Morrey \cite{MO}, Nirenberg \cite{NI} and Finn and Serrin \cite{F-S}. In this paper, we will demonstrate the asymptotic behavior of $K$-quasiconformal mappings at infinity over exterior domains (Cf. Theorem \ref{thm:Holder of exterior q-c} in Section 2). By using this result to (\ref{eq:F(D^2u)}) over exterior domains,
we shall not only show $D^2u$ has a limit $A$ at infinity, but get the decay rate of $|D^2u-A|$ as $|x|\rightarrow\infty$ as well. After this, Theorem 1.1 will be proved by standard arguments.
\newline
\indent The organization of this paper goes as follows. In section 2, we study the H\"{o}lder continuity and asymptotic behavior at infinity of $K$-quasiconformal mappings over exterior domains, which implies the gradient H\"{o}lder estimate and the gradient asymptotic behavior at infinity of solutions of linear elliptic equations over exterior domains. In section 3, we give the proof of Theorem \ref{thm:1}.
\section{Exterior $K$-quasiconformal mappings}
Let's begin with the definition of exterior $K$-quasiconformal mappings in $\mathbb{R}^2\setminus\bar{\Omega}$. We refer to \cite{G-T} for the original definition of $K$-quasiconformal mappings.
\begin{defn}
\label{def:quasiconformal exterior}
A mapping $w(x)=(p(x),q(x))$ from $\mathbb{R}^2\setminus\bar{\Omega}$ $(\Omega\subset\mathbb{R}^2\mbox{~is bounded~})$ in $x=(x_1,x_2)$ plane to $w=(p,q)$ plane is exterior $K$-quasiconformal in $\mathbb{R}^2\setminus\bar{\Omega}$ if $p, q\in C^1\left(\mathbb{R}^2\setminus\bar{\Omega}\right)$ and
\begin{eqnarray}
\label{eq:q-c}
p^2_1+p^2_2+q^2_1+q^2_2\leq 2K\left(p_1q_2-p_2q_1\right)
\end{eqnarray}
holds for all $x\in\mathbb{R}^2\setminus\bar{\Omega}$ with some constant $K>0$, where $p_i=\frac{\partial p(x)}{\partial x_i},q_i=\frac{\partial q(x)}{\partial x_i}, i=1,2$.
\end{defn}
For $K$-quasiconformal mappings, the apriori interior H\"{o}lder estimate is well known (Cf. \cite[Lemma 2]{NI} and \cite[Theorem 1]{F-S}).\newline
\indent For exterior $K$-quasiconformal mappings, we have the following H\"{o}lder estimate over exterior domain and the asymptotic behavior at infinity.
\begin{thm}
\label{thm:Holder of exterior q-c}
Let $w=(p,q)$ be exterior $K$-quasiconformal in $\mathbb{R}^2\setminus \bar{\Omega}$ $(\Omega\subset\mathbb{R}^2$ is bounded $)$ with $K\geq 1$, and suppose $|w|\leq M$. Then, for any $\Omega^{\prime}\supset\supset\Omega$ with $d=\mathrm{dist}(\Omega,\partial\Omega^{\prime})$,
\begin{equation*}
\left|w(x)-w(y)\right|\leq C\left|x-y\right|^{\alpha},x,y\in\mathbb{R}^2\setminus\overline{\Omega^{\prime}}.
\end{equation*}
and $w(x)$ tends to a limit $w(\infty)$ at infinity such that
\begin{equation}
\label{asymptotic of exterior q-c}
\left|w(x)-w(\infty)\right|\leq C|x|^{-\alpha}\mbox{~for any~}x\in\mathbb{R}^2\setminus\overline{\Omega^{\prime}},
\end{equation}
where $\alpha=K-(K^2-1)^{\frac 12}$, $C$ depends only on $K, d$ and $M$.
\end{thm}
\begin{re}
The results in Theorem \ref{thm:Holder of exterior q-c} are also valid for $p,q\in W_{\mathrm{loc}}^{1,2}(\mathbb{R}^2\setminus\bar{\Omega})\cap L^{\infty}(\mathbb{R}^2\setminus\bar{\Omega})$.
\end{re}
To prove Theorem \ref{thm:Holder of exterior q-c}, we first state the following H\"{o}lder continuity of $K$-quasiconformal mappings with singularities.
\begin{lemma}[\textnormal{\cite[Theorem 3]{F-S}}]
\label{le:interior Holder of q-c}
Let $w=(p,q)$ be $K$-quasiconformal in a domain $\Omega$ of $x=
(x_1,x_2)$ plane, except at a set $T$ of isolated points in $\Omega$. Assume $|w|\leq M$. Then $w$ can be defined, or redefined, at the points of $T$ so that the resulting function is continuous in $\Omega$, and in any compact subregion $\Omega^{\prime}$ of $\Omega$ with $d=\mathrm{dist}(\Omega^{\prime}, \partial\Omega)$, $w(x)$ satisfies a uniform H\"{o}lder inequality
\begin{equation}
\label{interior Holder of q-c}
|w(x)-w(y)|\leq C|x-y|^{\alpha}, x,y\in\Omega^{\prime},
\end{equation}
where $\alpha=K-(K^2-1)^{\frac 12}$, $C$ depends only on $K, d$ and $M$.
\end{lemma}
We prove Theorem \ref{thm:Holder of exterior q-c} by making use of the Kelvin transform. For this purpose, we establish the following lemma, which states that the Kelvin transform of an exterior $K$-quasiconformal mapping is $K$-quasiconformal with an isolated singularity.
\begin{lemma}
\label{le:transform}
Let $w=(p,q)$ be exterior $K$-quasiconformal in $\mathbb{R}^2\setminus\bar{B}_1(0)$. Let $\tilde{p}$ and $\tilde{q}$ be the \textit{Kelvin transform} of $p$ and $q$ respectively, namely
$$\tilde{p}(x)=p\left(\frac x{|x|^2}\right),\tilde{q}(x)=q\left(\frac x{|x|^2}\right), x\in B_1(0)\setminus\{0\}.$$
Then, $\tilde{w}=(\tilde{q},\tilde{p})$ is $K$-quasiconformal in $B_1(0)\setminus\{0\}$.
\end{lemma}
\begin{proof}
Calculating directly, we have
$$\tilde{p}_1=\left(|x|^{-2}-2x^2_1|x|^{-4}\right)p_1+\left(-2x_1x_2|x|^{-4}\right)p_2,$$
$$\tilde{p}_2=\left(-2x_1x_2|x|^{-4}\right)p_1+\left(|x|^{-2}-2x^2_2|x|^{-4}\right)p_2,$$
$$\tilde{q}_1=\left(|x|^{-2}-2x^2_1|x|^{-4}\right)q_1+\left(-2x_1x_2|x|^{-4}\right)q_2,$$
and
$$\tilde{q}_2=\left(-2x_1x_2|x|^{-4}\right)q_1+\left(|x|^{-2}-2x^2_2|x|^{-4}\right)q_2.$$
It's easy to see that
$$\tilde{p}^2_1+\tilde{p}^2_2+\tilde{q}^2_1+\tilde{q}^2_2=|x|^{-4}\left(p^2_1+p^2_2+q^2_1+q^2_2\right),$$
and
$$\tilde{p}_1\tilde{q}_2-\tilde{p}_2\tilde{q}_1=-|x|^{-4}\left(p_1q_2-p_2q_1\right).$$
Since $w=(p,q)$ is exterior $K$-quasiconformal over $\mathbb{R}^2\setminus\bar{B}_1(0)$, we deduce by Definition \ref{def:quasiconformal exterior} that $p$ and $q$ satisfy (\ref{eq:q-c}) in $\mathbb{R}^2\setminus\bar{B}_1(0)$ for some $K\geq 1$.
So, we obtain that in $B_1(0)\setminus\{0\}$,
$$\tilde{p}^2_1+\tilde{p}^2_2+\tilde{q}^2_1+\tilde{q}^2_2\leq 2K\left(\tilde{p}_2\tilde{q}_1-\tilde{p}_1\tilde{q}_2\right),$$
which implies $\tilde{w}=(\tilde{q},\tilde{p})$ is $K$-quasiconformal in $B_1(0)\setminus\{0\}$.
\end{proof}
\begin{proof}[Proof of Theorem \ref{thm:Holder of exterior q-c}] Assume without loss of generality that $B_1(0)\subset\Omega$. Let $\tilde{p}$ and $\tilde{q}$ be the Kelvin transform of $p$ and $q$ respectively given by Lemma \ref{le:transform}. Let $\hat{\Omega}=\left\{\frac {x}{|x|^2}\Big|x\in\mathbb{R}^2\setminus\bar{\Omega}\right\}$ and for any $\Omega^{\prime}\supset\supset\Omega$, $\tilde{\Omega}=\left\{\frac {x}{|x|^2}\Big|x\in\mathbb{R}^2\setminus\overline{\Omega^{\prime}}\right\}$. Then by Lemma \ref{le:transform}, $\tilde{w}=(\tilde{q},\tilde{p})$ is $K$-quasiconformal in $\hat{\Omega}\setminus\{0\}$ with $K\geq 1$. Since $|w|\leq M$ implies $|\tilde{w}|\leq M$, applying Lemma \ref{le:interior Holder of q-c} to $\tilde{w}$ with $T=\{0\}$, we know that
$$|\tilde{w}(x)-\tilde{w}(y)|\leq C|x-y|^{\alpha}, x,y\in{\tilde{\Omega}},$$
which implies that $\tilde{w}(x)$ has a limit $\tilde{w}(0)$ at $0$ and for all $x\in{\tilde{\Omega}},$
$$\left|\tilde{w}(x)-\tilde{w}(0)\right|\leq C|x|^{\alpha}, \alpha=K-\left(K^2-1\right)^{\frac 12}.$$
Transforming back to exterior domain, we have that
$$|w(x)-w(y)|\leq C|x-y|^{\alpha}, x,y\in\mathbb{R}^2\setminus\overline{\Omega^{\prime}}$$
and $w(x)$ has a limit $w(\infty)=\tilde{w}(0)$ at infinity with
$$\left|w(x)-w(\infty)\right|\leq C|x|^{-\alpha},x\in\mathbb{R}^2\setminus\overline{\Omega^{\prime}},$$
where $\alpha=K-(K^2-1)^{\frac 12}$, $C$ depends only on $K, d$ and $M$.\newline
\indent The theorem is therefore proved.
\end{proof}
Next we consider linear elliptic equation
\begin{equation}
\label{eq:L}
L(u)=a_{11}(x)u_{11}(x)+2a_{12}(x)u_{12}(x)+a_{22}(x)u_{22}(x)=0,
\end{equation}
where $L$ is uniformly elliptic, that is, there exist $0<\lambda\leq\Lambda$ such that
\begin{equation}
\label{uniform elliptic 1}
\lambda(\xi_1^2+\xi_2^2)\leq a_{11}\xi_1^2+2a_{12}\xi_1\xi_2+a_{22}\xi_2^2\leq \Lambda(\xi_1^2+\xi_2^2), \forall \xi=(\xi_1,\xi_2)\in\mathbb{R}^2
\end{equation}
and
\begin{equation}
\label{uniform elliptic 2}
\frac{\Lambda}{\lambda}\leq \gamma
\end{equation}
for some constant $\gamma\geq 1$.\newline
\indent For uniformly elliptic equation (\ref{eq:L}) in a domain $\Omega$ of $\mathbb{R}^2$, it follows from the interior H\"{o}lder estimate of $K$-quasiconformal mappings that its bounded solutions have interior $C^{1,\alpha}$ estimate\cite[Theorem 12.4]{G-T}.\newline
\indent For uniformly elliptic equation (\ref{eq:L}) over exterior domain in $\mathbb{R}^2$, we can establish the gradient H\"{o}lder estimate and the gradient asymptotic behavior of solutions at infinity by the virtue of Theorem \ref{thm:Holder of exterior q-c}.
\begin{thm}
\label{thm:exterior for equation}
Let $\Omega$ be a bounded domain of $\mathbb{R}^2$ and $u\in C^2(\mathbb{R}^2\setminus \bar{\Omega})$ be a solution of equation (\ref{eq:L}) in $\mathbb{R}^2\setminus \bar{\Omega}$. Suppose $|Du(x)|\leq M$. Then for any $\Omega^{\prime}\supset\supset\Omega$ with $d=\mathrm{dist}(\Omega,\partial\Omega^{\prime})$,
\begin{equation*}
\left|Du(x)-Du(y)\right|\leq C\left|x-y\right|^{\alpha}, x,y\in\mathbb{R}^2\setminus\overline{\Omega^{\prime}}
\end{equation*}
and $Du(x)$ has a limit $Du(\infty)$ at infinity with
\begin{equation}
\label{asymptotic of Du}
|Du(x)-Du(\infty)|\leq C|x|^{-\alpha}, x\in\mathbb{R}^2\setminus\overline{\Omega^{\prime}},
\end{equation}
where $\alpha$ depends only on $\gamma$, $C$ depends only on $\gamma, d$ and $M$.
\end{thm}
\begin{re}
The results in Theorem \ref{thm:exterior for equation} are also valid for $u\in W^{2,2}(\mathbb{R}^2\setminus\bar{\Omega})$.
\end{re}
\begin{proof}[Proof of Theorem \ref{thm:exterior for equation}]
\indent Assume without loss of generality that $\lambda=1$. Let $p=u_1, q=u_2$. By equation (\ref{eq:L}), (\ref{uniform elliptic 1}) and (\ref{uniform elliptic 2}), we have (see details in \cite{G-T})
$$p^2_1+p^2_2\leq a_{11}p^2_1+2a_{12}p_1p_2+a_{22}p^2_2=a_{22}J, J=p_2q_1-p_1q_2, x\in \mathbb{R}^2\setminus \bar{\Omega}$$
and
$$q^2_1+q^2_2\leq a_{11}J, x\in \mathbb{R}^2\setminus \bar{\Omega}.$$
Noticing that $2\leq a_{11}+a_{22}=1+\Lambda\leq 1+\gamma$, we arrive at
$$p^2_1+p^2_2+q^2_1+q^2_2\leq \left(a_{11}+a_{22}\right)J\leq \left(1+\gamma\right)J, x\in \mathbb{R}^2\setminus \bar{\Omega},$$
which implies that $w=(q,p)$ is exterior $K$-quasiconformal over $\mathbb{R}^2\setminus \bar{\Omega}$ with $K=\frac{1+\gamma}{2}$. Since $|Du|\leq M$ in $\mathbb{R}^2\setminus\bar{\Omega}$, Theorem \ref{thm:Holder of exterior q-c} therefore asserts that for any $\Omega^{\prime}\supset\supset\Omega$,
$$|Du(x)-Du(y)|\leq C|x|^{-\alpha}, x,y\in\mathbb{R}^2\setminus\overline{\Omega^{\prime}}$$
and $Du(x)$ tends to a limit $Du(\infty)=(p(\infty), q(\infty))$ at infinity with
$$|Du(x)-Du(\infty)|\leq C|x|^{-\alpha}, x\in\mathbb{R}^2\setminus\overline{\Omega^{\prime}},$$
where $\alpha$ depends only on $\gamma$, $C$ depends only on $\gamma, d$ and $M$.
\end{proof}
\section{Exterior Bernstein type theorem}
In this section, we give the proof of the exterior Bernstein type theorem, i.e., Theorem \ref{thm:1}. As we remarked before, we don't need the concavity or convexity of $F$.\newline
\indent We find the limit $A$ of the Hessian $D^2u$ at infinity and estimate the decay rate of $|D^2u-A|$ first.
\begin{thm}
\label{thm:limit of D^2u}
Let $u$ be as in Theorem \ref{thm:1}. Then there exists a symmetric matrix
$A\in\mathbb{R}^{2\times2}$ such that
$$D^2u(x)\to A\text{~as~}|x|\to\infty$$ and
$$|D^2u(x)-A|\leq C|x|^{-\alpha}\text{~as~}|x|\to\infty,$$
which implies
\begin{eqnarray}
\label{in:u-xAx}
\left|u(x)-\frac 12 x^{\mathrm{T}}Ax\right|\leq C|x|^{2-\alpha}\text{~as~}|x|\to\infty,
\end{eqnarray}
where $\alpha\in(0,1)$ is a constant depending only on $\lambda$ and $\Lambda$, $C$ is a positive constant depending only on $\lambda$, $\Lambda$, and $M$.
\end{thm}
\begin{re}
If $u\in C^2$, then we don't need $F\in C^{1,1}$ in Theorem \ref{thm:limit of D^2u}.
\end{re}
\begin{proof}[\textit{Proof of Theorem \ref{thm:limit of D^2u}}]
By the virtue of the Nirenberg estimate, we can see that viscosity solutions to the equation (\ref{eq:F(D^2u)}) in $\mathbb{R}^2$ are always $C^{2,\alpha}$ for some $\alpha\in(0,1)$ depending only on the ellipticity constants of $F$. It follows from $F\in C^{1,1}$ and the Schauder estimate that $u\in C^{3,\gamma}(\mathbb{R}^2\setminus\bar{\Omega})$ for any $\gamma\in(0,1)$.
Then we take derivative with respect to $x_k$ $(k=1,2)$ on both sides of equation (\ref{eq:F(D^2u)}) to obtain
\begin{align}
\label{eq:aij}
a_{ij}(x)v_{ij}(x)=0, x\in\mathbb{R}^2\setminus\bar{\Omega},
\end{align}
where $a_{ij}(x)=F_{M_{ij}}\left(D^2u(x)\right)$ and $v(x)=u_k(x)$.
\newline
\indent Since $\|D^2u\|_{L^{\infty}\left(\mathbb{R}^2\setminus\bar{\Omega}\right)}\leq M$, we know $|Dv(x)|\leq M$. Applying Theorem \ref{thm:exterior for equation} to equation (\ref{eq:aij}) in $\mathbb{R}^2\setminus\bar{\Omega}$, we have that $Dv(x)$ tends to a limit $Dv(\infty)$ at infinity and for any $\Omega^{\prime}\supset\supset\Omega$,
$$|Dv(x)-Dv(\infty)|\leq C|x|^{-\alpha}, x\in\mathbb{R}^2\setminus\overline{\Omega^{\prime}}.$$
Then by the arbitrarity of $k$, we conclude that there exists a symmetric matrix $A\in\mathbb{R}^{2\times 2}$ such that $D^2u(x)\to A$ as $|x|\to\infty$ and
$$\left|D^2u(x)-A\right|\leq C|x|^{-\alpha} \text{~as~}|x|\to\infty.$$
It follows that
$$\left|u(x)-\frac 12 x^{\mathrm{T}}Ax\right|\leq C|x|^{2-\alpha}\text{~as~}|x|\to\infty,$$
where $\alpha\in(0,1)$ depends only on $\lambda$ and $\Lambda$, $C>0$ depends only on $\lambda$, $\Lambda$ and $M$.
\end{proof}
\indent Based on Theorem \ref{thm:limit of D^2u}, we will find the finer asymptotic behavior of $u$ by standard arguments. To do this, we need the following three lemmas which are well known. For readers' convenience, we show the proofs of them. Lemma \ref{le:smoothness} gives the higher order estimates. Lemma \ref{le:iterate} and Lemma \ref{le:expansion} are used to determine the linear term, logarithm term and constant term of the asymptotics of $u$.
\begin{lemma}
\label{le:smoothness}
Let $\phi$ be a viscosity solution of the equation
$$F\left(D^2\phi(x)+A\right)=0, x\in\mathbb{R}^2\setminus \bar{B}_1(0),$$
where $F\in C^{1,1}$ is a fully nonlinear uniformly elliptic operator with ellipticity constants $\lambda$ and $\Lambda$, and $A\in\mathbb{R}^{2\times 2}$ is symmetric matrix, satisfying $F(A)=0$. Suppose that for some constants $\beta>0$ and $\rho<2$,
$$|\phi(x)|\leq \beta|x|^{\rho}, x\in\mathbb{R}^2\setminus \bar{B}_1(0).$$
Then there exists some constant $r=r(\beta, \rho)\geq 1$ such that for $k=0,1,2,3$,
$$\left|D^k\phi(x)\right|\leq C|x|^{\rho-k}, x\in\mathbb{R}^2\setminus \bar{B}_r(0),$$
where $C$ depends only on $\lambda$, $\Lambda$, $\beta$ and $\rho$.
\end{lemma}
\begin{proof}
By $F\in C^{1,1}$, the Nirenberg estimate and the Schauder estimate, $\phi(x)\in C^{3,\gamma}$ for any $\gamma\in(0,1)$.
Fix $x\in\mathbb{R}^2\setminus\bar{B}_1(0)$ with $|x|>6$ and let
$$\bar{\phi}(y)=\left(\frac {2}{|x|}\right)^2 \phi\left(x+\frac{|x|}{2}y\right), y\in B_1(0).$$
\indent Since $$F(A)=0$$ and $$F(D^2\bar{\phi}(y)+A)=0, y\in B_1(0),$$ we see that
$$\bar{a}_{ij}(y)\bar{\phi}_{ij}(y)=0, y\in B_1(0),$$
where $\bar{a}_{ij}(y)=\int_0^1F_{M_{ij}}\left(tD^2\bar{\phi}(y)+A\right)\mathrm{d}t$. By the Schauder estimate, we have that for $k=0,1,2,3$,
$$\left|D^k\bar{\phi}(0)\right|\leq\|\bar{\phi}\|_{L^{\infty}(\bar{B}_1(0))}\leq C|x|^{\rho-2},$$
which implies
$$\left|D^k\phi(x)\right|\leq C|x|^{\rho-k},$$
where $C$ depends only on $\lambda$, $\Lambda$, $\beta$ and $\rho$.
\end{proof}
\begin{lemma}
\label{le:iterate}
Suppose $f(x)=O(|x|^{-\beta})$ as $|x|\to\infty$ with $\beta>1$. Then for any $\varepsilon>0$, the equation
$$\Delta u(x)=f(x)\text{~in~}\mathbb{R}^2\setminus \bar{B}_1(0)$$
has a solution $u(x)=O(|x|^{2-\beta+\varepsilon})$ as $|x|\to\infty$.
\end{lemma}
\begin{proof}
Let $$u(x)=-\frac {1}{2\pi}\int\limits_{\mathbb{R}^2\setminus \bar{B}_1(0)}(\log{|x-y|-\log{|y|}})f(y)\mathrm{d}y.$$
Then
$$\Delta u(x)=f(x), x\in\mathbb{R}^2\setminus \bar{B}_1(0)$$
and for any $\varepsilon>0$,
$$\left|u(x)\right|\leq C(\varepsilon)|x|^{2-\beta+\varepsilon}, x\in\mathbb{R}^2\setminus \bar{B}_1(0).$$
\end{proof}
\begin{lemma}
\label{le:expansion}
Let $u(x)=O(|x|^{\beta})$ be a smooth solution of $$\Delta u(x)=0, x\in\mathbb{R}^2\setminus \bar{B}_1(0)$$ for some $0<\beta<2$.
Then
\begin{equation}
\label{expansion of u}
u=b\cdot x+d\log{|x|}+c+O\left(|x|^{-1}\right)\mbox{~as~}|x|\to\infty,
\end{equation}
where $b\in\mathbb{R}^2$, $c, d\in\mathbb{R}$. Particularly, for $0<\beta<1$, (\ref{expansion of u}) holds with $b=0$.
\end{lemma}
\begin{proof}
Let $\xi(z)=u_1(x)-iu_2(x), z=x_1+ix_2$. Then $\xi(z)$ is an analytic function in $\mathbb{R}^2\setminus \bar{B}_1(0)$ and the growth of $\xi(z)$ is at most of order $|z|^{\beta-1}$. Since $0<\beta<2$, the Laurent expansion of $\xi(z)$ has the form
\begin{equation}
\label{laurent expasion}
\xi(z)=a_0+a_{-1}z^{-1}+a_{-2}z^{-2}+\cdots, z\in\mathbb{R}^2\setminus\bar{B}_1(0),
\end{equation}
where $a_0, a_{-1}, a_{-2}, \cdots$ are all complex numbers. Thus we have
$$Du(x)=D(b\cdot x+c_1)+D(a_{-1}\log{|x|}+c_2)+O(|x|^{-2})\text{~as~}|x|\to\infty,$$
where $b=(\mathrm{Re}~a_0, -\mathrm{Im}~a_0)^{\mathrm{T}}, c_1, c_2\in\mathbb{R}$. Since $\mathrm{Re}\int a_{-1}z^{-1}=\mathrm{Re}(a_{-1}\log{z})$ as a part of expansion of a real function $u$, $a_{-1}$ must be a real number.
Integrating the above, we see that
$$u=b\cdot x+d\log{|x|}+c+O(|x|^{-1})\text{~as~}|x|\to\infty,$$
where $c\in\mathbb{R}, d=a_{-1}\in\mathbb{R}$.\newline
\indent Particularly, for $0<\beta<1$, (\ref{laurent expasion}) holds with $a_0=0$. Therefore, the above equality also holds with $b=0$.
\end{proof}
\begin{proof}[Proof of Theorem \ref{thm:1}]We divide the proof into six steps.
\ \newline
\indent\textit{Step 1. Improving estimate (\ref{in:u-xAx}).}\newline
\indent Let $$\varphi(x)=u(x)-\frac 12 x^{\mathrm{T}}Ax.$$
Then by Theorem \ref{thm:limit of D^2u}, $$\varphi(x)=O(|x|^{2-\alpha})$$ and $\varphi(x)$ satisfies
\begin{equation}
\label{eq:F(D^2 varphi+A)}
F(D^2\varphi(x)+A)=0, x\in\mathbb{R}^2\setminus\bar{\Omega}.
\end{equation}
Suppose $R_0\geq 1$ such that $\Omega\subset B_{R_0}(0)$. It follows from Lemma \ref{le:smoothness} that for all $x\in\mathbb{R}^2\setminus\bar{B}_{R_0}(0)$,
\begin{eqnarray}
\left|D\varphi(x)\right|\leq C|x|^{1-\alpha},
\left|D^2\varphi(x)\right|\leq C|x|^{-\alpha},
\left|D^3\varphi(x)\right|\leq C|x|^{-1-\alpha}.
\label{deri}
\end{eqnarray}
\indent Taking derivative to both sides of equation (\ref{eq:F(D^2 varphi+A)}) with respect to $x_k$ $(k=1,2)$, we know that $\varphi_k$ satisfies equation
\begin{eqnarray}
a_{ij}(x)\left(\varphi_k(x)\right)_{ij}=0, x\in \mathbb{R}^2\setminus\bar{B}_{R_0}(0),
\label{eq:linear 1}
\end{eqnarray}
where $a_{ij}(x)=F_{M_{ij}}\left(D^2\varphi(x)+A\right)$. Since it follows from Theorem \ref{thm:limit of D^2u} that $D^2\varphi(x)\to 0$ as $|x|\to\infty$, we know
\begin{equation}
a_{ij}(x)\to F_{M_{ij}}(A)\mbox{~as~}|x|\to\infty.
\end{equation}
Assuming without loss of generality that $F_{M_{ij}}(A)=\delta_{ij}$, then by $F\in C^{1,1}$,
\begin{equation}
\left|\delta_{ij}-a_{ij}\right|\leq C|x|^{-\alpha}
\end{equation}
for some $C>0$. We obtain that for all $x\in\mathbb{R}^2\setminus\bar{B}_{R_0}(0)$,
$$\varphi_k(x)=O(|x|^{1-\alpha})$$ and
\begin{equation}
\label{eq:Delta varphi k}
\Delta(\varphi_k)(x)=\left(\delta_{ij}-a_{ij}(x)\right)(\varphi_k)_{ij}(x)=O(\left|x|^{-\alpha}|x|^{-1-\alpha}\right)=O\left(|x|^{-1-2\alpha}\right). \end{equation}
\indent By Lemma \ref{le:iterate}, for any $0<\varepsilon<\alpha$, there exists $$v(x)=O(|x|^{1-2\alpha+\varepsilon})$$
satisfying the equation (\ref{eq:Delta varphi k}). Then
\begin{equation}
\Delta (\varphi_k-v)(x)=0, x\in\mathbb{R}^2\setminus\bar{B}_{R_0}(0)
\end{equation}
and
$$\varphi_k(x)-v(x)=O(|x|^{1-\alpha}).$$
Therefore Lemma \ref{le:expansion} states
$$\varphi_k(x)-v(x)=d\log{|x|}+c+O\left(|x|^{-1}\right)\mbox{~as~}|x|\to\infty$$
for some $b\in\mathbb{R}^2, c\in\mathbb{R}$. Hence, for $k=1,2$, $$\varphi_k(x)=O(|x|^{1-2\alpha+\varepsilon}).$$
By the arbitrarity of $k$, we see $$\varphi(x)=O(|x|^{2-2\alpha+\varepsilon}).$$
Since $0<\varepsilon<\alpha$, we have improved the estimate (\ref{in:u-xAx}) a little.\newline
\indent We repeat the arguments above $n$ times, where $n$ is determined by the following way. Fix $0<\varepsilon<\alpha$ and let $n$ be an integer such that $0<1-2^n\alpha+(2^n-1)\varepsilon<\frac 18$, i.e. $n=\left[\log_2{\frac{\frac 78-\varepsilon}{\alpha-\varepsilon}}\right]+1$. Then we get an appropriate improved estimate
$$\varphi(x)=O(|x|^{2-2^n\alpha+(2^n-1)\varepsilon})=O(|x|^{1+\delta}), x\in\mathbb{R}^2\setminus\bar{B}_{R_0}(0)$$
with $\delta=1-2^n\alpha+(2^n-1)\varepsilon<\frac 18$.\newline
\indent\textit{Step 2. Determining the linear term.}\newline
\indent We obtain by Lemma \ref{le:smoothness} that for $\delta\in(0,\frac 18)$ and all $x\in\mathbb{R}^2\setminus\bar{B}_{R_0}(0)$,
$$|D\varphi(x)|\leq C|x|^{\delta}, |D^2\varphi(x)|\leq C|x|^{-1+\delta}.$$
Since $\varphi(x)$ satisfies equation
\begin{equation}
\label{eq:linear 2}
\bar{a}_{ij}(x)\varphi_{ij}(x)=0, x\in\mathbb{R}^2\setminus\bar{B}_{R_0}(0),
\end{equation}
where $\bar{a}_{ij}(x)=\int_0^1F_{M_{ij}}\left(tD^2\varphi(x)+A\right)\mathrm{d}t$, it follows from $F\in C^{1,1}$ that for some $C>0$,
$$|\bar{a}_{ij}(x)-\delta_{ij}|\leq C|x|^{-1+\delta}.$$
Thus
$$\Delta \varphi(x)=\left(\delta_{ij}-\bar{a}_{ij}(x)\right)\varphi_{ij}(x)=O \left(|x|^{-2+2\delta}\right), x\in\mathbb{R}^2\setminus\bar{B}_{R_0}(0).$$
Then Lemma \ref{le:iterate} implies that for any $\varepsilon\in(0,\frac 18)$, there exists $$v(x)=O(|x|^{2\delta+\varepsilon}),$$ satisfying
$$\Delta(\varphi-v)(x)=0, x\in\mathbb{R}^2\setminus\bar{B}_{R_0}(0).$$
Since $$\varphi(x)-v(x)=O(|x|^{1+\delta}),$$
it follows from Lemma \ref{le:expansion} that there exists $b\in\mathbb{R}^2$ such that
$$\varphi(x)-v(x)=b\cdot x+O(\log{|x|}).$$
Hence $$\varphi(x)=b\cdot x+O(|x|^{2\delta+\varepsilon}).$$
\indent\textit{Step 3. Determining the logarithm term and constant term.}\newline
\indent Let $$\bar{\varphi}(x)=u-\left(\frac 12x^{\mathrm{T}}Ax+b\cdot x\right).$$
Then $$\bar{\varphi}(x)=O(|x|^{2\delta+\varepsilon})$$ and $\bar{\varphi}(x)$ satisfies equation (\ref{eq:linear 2}).\newline
\indent By Lemma \ref{le:smoothness}, we see that for all $x\in\mathbb{R}^2\setminus\bar{B}_{R_0}(0)$,
$$|D\bar{\varphi}(x)|\leq C|x|^{-1+2\delta+\varepsilon}, |D^2\bar{\varphi}(x)|\leq C|x|^{-2+2\delta+\varepsilon}.$$
Consequently, for some $C>0$,
$$|\bar{a}_{ij}-\delta_{ij}|\leq C|x|^{-2+2\delta+\varepsilon}$$
and $$\Delta\bar{\varphi}(x)=(\delta_{ij}-\bar{a}_{ij})\bar{\varphi}_{ij}=O(|x|^{-4+4\delta+2\varepsilon}).$$
Since $\delta, \varepsilon\in (0,\frac 18)$, then by Lemma \ref{le:iterate}, there exists
$$v(x)=O(|x|^{-2+\varepsilon^{\prime}})$$
with $\varepsilon^{\prime}\in(0,1)$, satisfying
$$\Delta(\bar{\varphi}-v)(x)=0$$ and
$$\bar{\varphi}(x)-v(x)=O(|x|^{2\delta+\varepsilon}).$$
Thus, Lemma \ref{le:expansion} leads to
$$\bar{\varphi}(x)=d\log{|x|}+c+O\left(|x|^{-1}\right) \mbox{~as~}|x|\to\infty$$
for some $c, d\in\mathbb{R}$, namely,
\begin{equation}
\label{asymptotic of u}
u(x)=\frac 12 x^{\mathrm{T}}Ax+b\cdot x+d\log{|x|}+c+O(|x|^{-1}).
\end{equation}
\indent\textit{Step 4. Determining the $\frac {x}{|x|^2}$ term.}\newline
\indent Let $$\hat{\varphi}(x)=u(x)-\left(\frac 12 x^{\mathrm{T}}Ax+b\cdot x+d\log{|x|}+c\right).$$
Then $$D^2\hat{\varphi}=D^2u-A+O(|x|^{-2}).$$
By (\ref{asymptotic of u}), $D^2u=A+O(|x|^{-2})$, which implies $$\left|D^2\hat{\varphi}\right|=O(|x|^{-2}).$$ Since $\hat{\varphi}(x)$ satisfies equation (\ref{eq:linear 2}) with $\bar{a}_{ij}(x)=\int_0^1F_{M_{ij}}\left(t\left(D^2\hat{\varphi}(x)+D^2(d\log{|x|})\right)+A\right)\mathrm{d}t$, we have that for some $R_0\geq 1$ such that $\Omega\subset B_{R_0}(0)$, $$\Delta\hat{\varphi}(x)=(\bar{a}_{ij}(x)-\delta_{ij})\hat{\varphi}_{ij}(x)=:f(x)=O(|x|^{-2}|x|^{-2})=O(|x|^{-4}), x\in\mathbb{R}^2\setminus\bar{B}_{R_0}(0).$$
\indent Let $\psi(x)=\hat{\varphi}(\frac {x}{|x|^2})$ and $\tilde{f}(x)=f(\frac {x}{|x|^2})$ be the Kelvin transform of $\hat{\varphi}(x)$ and $f(x)$ respectively. Then we see $$\psi(x)=O(|x|)$$ and
$$\Delta\psi(x)=|x|^{-4}\tilde{f}(x)=:g(x)=O(1), x\in B_{\frac{1}{R_0}}(0).$$
\indent From $g\in L^p(B_{1/R_0}(0))$ for any $p>2$, it follows that $\psi(x)\in W^{2,p}(B_{1/R_0}(0))$ and hence $\psi(x)\in C^{1,\alpha}(B_{1/R_0}(0))$ for $\alpha=1-\frac{2}{p}\in(0,1)$. Then there exists $e\in\mathbb{R}^2$ and $\tilde{c}\in\mathbb{R}$ such that for some $C>0$,
$$\left|\psi(x)-(e\cdot x+\tilde{c})\right|\leq C|x|^{1+\alpha},x\in B_{\frac {1}{R_0}}(0).$$
Since $\psi(0)=0$ implies $\tilde{c}=0$, we go back to exterior domain to get
$$\left|\hat{\varphi}(x)-e\cdot\frac{x}{|x|^2}\right|\leq C|x|^{-1-\alpha},x\in\mathbb{R}^2\setminus\bar{B}_{R_0}(0),$$
which leads to
$$u=\frac 12 x^{\mathrm{T}}Ax+b\cdot x+d\log{|x|}+c+e\frac {x}{|x|^2}+O(|x|^{-1-\alpha}).$$
\indent\textit{Step 5. Calculating the value of $d$.}\newline
\indent Let $Q(x)=\frac 12 x^{\mathrm{T}}Ax+b\cdot x+c$. Then $$u(x)=Q(x)+d\log{|x|}+O(|x|^{-1})$$
and
$$\Delta(u-Q)(x)=O(|x|^{-3})$$ is integrable. Let $\nu$ be the unit outward normal of boundaries $\partial\Omega$ and $C_R=\partial B_R(0)$. Then by the divergence theorem, we have that for some $R>0$ large enough,
\begin{equation*}
\begin{split}
\iint\limits_{{B_R(0)\setminus\bar{\Omega}}}\Delta(u-Q)(x)\mathrm{d}x_1\mathrm{d}x_2&=\int\limits_{\partial({B_R(0)\setminus\bar{\Omega}})}(u-Q)_{\nu}\mathrm{d}s\\
&=\int\limits_{C_R}(d\log{|x|}+O(|x|^{-1}))_{\nu}(x)\mathrm{d}s-\int\limits_{\partial\Omega}(u-Q)_{\nu}\mathrm{d}s\\
&=d\int\limits_{C_R}\frac{x}{|x|^2}\cdot\nu\mathrm{d}s+O\left(\frac 1R\right)-\int\limits_{\partial\Omega}u_{\nu}\mathrm{d}s+\int_{\partial\Omega}Q_{\nu}\mathrm{d}s\\
&=2\pi d+O\left(\frac 1R\right)-\int\limits_{\partial\Omega}u_{\nu}\mathrm{d}s+\int_{\Omega}\Delta Q\mathrm{d}x\\
&=2\pi d+O\left(\frac 1R\right)-\int\limits_{\partial\Omega}u_{\nu}\mathrm{d}s+\mathrm{tr}A|\Omega|.
\end{split}
\end{equation*}
Letting $R\to\infty$, we get (\ref{value of d}).\newline
\indent\textit{Step 6. Improving smoothness of the error.}\newline
\indent Furthermore, suppose $F$ is smooth. Let
$$\tilde{\varphi}(x)=u-\left(\frac 12 x^{\mathrm{T}}Ax+b\cdot x+d\log{|x|}+c+e\frac {x}{|x|^2}\right).$$
Then, the Schauder estimate asserts that for all $k\in\mathbb{N}$,
$$\left|D^k\tilde{\varphi}(x)\right|\leq C(k)|x|^{-1-\alpha-k}.$$
\indent We complete the proof of Theorem \ref{thm:1}.
\end{proof}
\begin{re}(\romannumeral 1). If the equation has some divergence structure, then we can obtain another representation for the constant $d$, for example, the Monge-Amp\`{e}re equations, the special Lagrangian equations and the inverse harmonic Hessian equations. We refer to \cite{C-LI} and \cite{LI-LI-Y} to see details.\newline
\indent(\romannumeral 2). By the virtue of Theorem \ref{thm:1}, we have expansion for the solutions to the Monge-Amp\`{e}re equations, the special Lagrangian equations and the inverse harmonic Hessian equations at infinity in $\mathbb{R}^2\setminus\bar{\Omega}$, namely, any solution tends to a quadratic polynomial plus a logarithm term and $e\frac {x}{|x|^2}$ with the error at least $|x|^{-1-\alpha}$, which is finer than the results in \cite{C-LI} and \cite{LI-LI-Y}.
\end{re}
\end{document} | math |
वो राहगिर जगह-जगह घूम आयेगा
कभी-कभी प्यार इंसान को उस ऊँचाई तक ले जाती है
जब वो अपने दायरे को लाँघ कर आगे निकल जाती है
फिर वो किसी एक की नहीं रेह जाती....
रोज़मरे की बातों से हटकर कुछ गुलाबी एहसासों को
पिरोने की एकमात्र कोशिश है....
आप की राय की मुंतजि़र
तुम्हारे प्यार के बरसात की एक बूँद
समेट लिया है मैंने मेरे आँचल में
आज एक बीज बनकर ही सही
कल एक कँवल बन के खिलेगा
अपनी खुशियों की दास्तान
वो सुनायेगा सभी को
दिलाकर एहसास हमारे प्यार का
क्या ज़माना बदल गया?
बहुत दिनों बाद आज कुछ लिखने का अवसर प्राप्त हुआ !
कभी वक्त ने तो कभी हालात ने इसे मनसूब होने न दिया ः)वो यादें अक्सर अच्छी और मीठीं होती हैं, जो खुशियों से भरी हुईं रही हों
और तभी तो इंसान यादों को आज भी सँजोये रखता है !
कुछ आज की तो कुछ बचपन की यादों में छिपे फर्क को मेहसूस किया है
आप की राय की मुंतजिर.....
कैसा ज़माना था वो
जब लोग होली-ईद-दिवाली
सब मिलकर मनाते थे
किसने देखा, खुशियों का
एक मेला जैसा लगता था
तब मौसम भी सुहाना था
वक्त जैसे पडा रेहता
जिसे चाहे वो उसे
उठा लेता और समा जाता उसमें
आज कितना बदल सा गया है
सब कुछ कितना मुश्किल सा
न वक्त कहीं नज़र आता है
न मौसम पुराना सा
होली-ईद-दिवाली तो दूर
जन्मदिन भी नहीं मनाया जाता
कौन कहाँ वक्त निकाले
इन झमेलों में
आज हर कोई पूछता है
दोस्ती का हाथ बढाता है
सिर्फ कमाई-साधन के लिए
किस दोस्ती का फल व्यापार बने
आज न वक्त है
न वो लोग जिन्हें
कभी सादगी पसंद
न ही खुशियाँ
फिर भी निकल पडे हैं
ढुँढने अपने वज़ूद को
पैसों की आड में
खुशकिस्मती बनाने में
मैं सोचती रेहती हूँ
या मैं ज़माने में
कुछ देर से आई !?!
ज़िंदगी तेरे तो खेल निराले हैं
ये कविता मैंने तब लिखी थी जब लेबन्न में लडाई छिङ गई थी । जहॉ बच्चों की लाशें गिर रही थीं...और इस तरफ
एक मासूम बच्चा अपने पापा की ऊँगलियाँ पकड कर पारकींग लॉट पर चला जा रहा था....
ज़िंदगी तुझ से कोई शिकायत नहीं
क्योंकि, तुने वो सब दिया
जो कभी मैंने माँगा नहीं और
जो कभी मैंने चाहा भी नहीं
कितना इंसाफ है तेरी जूस्तज़ू में
जो कभी अपना तो क्या
पराया भी नहीं जताता
मैं सोच में रेहती हूँ ज़िंदगी
तू मेरा अपना है या पराया?
तू तो हवा का झोंका है
जो कभी ठंडी हवा से
दिल मचला दे तो
कभी तूफान बनकर
खडा हो जाऐ।
तुझे मैं क्या कहूँ -
आ देखें तेरी अगली चाल क्या है ।?।
आज भी लकडियाँ बँटोरता हूँ...
आज के युग में जो भी हो रहा है....उन सभी को मद्दे नज़र रखते हुए येही कुछ लिख बन पाया हमसे...आप सभी के
इसिलाह की मुंतजि़र.....
लकडियॉ बिन ने आया था किसी रोज़
काले बादलों का कॉरवॉ आता देख
छोड गया इन्हें ये सोच..
कल फिर आॐगा !
आज नया दिन है..पहाडों की परछाई के पीछे से
किरण झॉक रही थी और शुश्क हवा
अँगिठी के पास बैठने का बहाना दे रही थी !
याद आया, आज फिर लकडियॉ बिननी है
सुना है इस बार जा़डे की सरदी कुछ लम्बी है
लकडियों पर ओस की मोतियॉ
मानों लडी बनाकर बैठीं हों !
मैंने एक नहीं मानी-गिली ही सही
उठा लाया उन्हें जलाने के वास्ते...
सुबह उठा तो देखा लकडियों पर
हरी-हरी पत्तियों की कोपलें निकल आईं हैं
मानो मरे हुये में जान आ गई !
फिर दिल न माना कुछ और सोचने
निकाल फेंका बगीचे में, के
फूलो-फलो तुम भी बगीया के किसी कोने में
बन जाओ एक इसी गुलिस्तॉ में !
फिर सोचने लगा मैं -उस दिन बादलों को देख...गर मैं
खाली हाथ न चला आता
तो शायद ये राख का ढेर बनी रेहतीं
मैं कुछ और गरम आँच सेख लेता....लेकिन फिर सोचा -
जीवन-दान की जो आँच में सुकून है
वो किसी आग की आँच में कहॉ?
जिंदगी में हर कोई अपने- अपने अरमान लिये हुये आता है और शायद उसे पूरा करने या होने की आरजू़ में ही जिंदगी गुजा़र देता है...मेरी भी कोशिश यहाँ उन आरजूओं की सोच, कल्पना और उन सोचों में पडे़ एहसासों को पेश करना है। कहाँ तक सफल हुई हूँ ये मैं आप सभी पर छोड़ती हूँ......
ख्यालों के पन्ने उलटती रेहती हूँ
जिंदगी की स्याही घिसती रेहती हूँ
नये पन्ने जोड़ने की आरजू़ में,
नीत-नये दिन खोजती रेहती हूँ
जीवन के पुस्तकालय में,
'मधुशाला' को ढुँढती रेहती हूँ
शब्दकोश के इस भँडार से
जीवनरस निचोडती रेहती हूँ
स्याही-कलम के बिना भी
लिखे गये हैं ग्रंथ कई
मेरे कलम में आज भी मैं,
रंग भरती रेहती हूँ
अब के खुशियों से भरे
जीवन की हकीकत पर
उपन्यास लिखने की
आरजू़ में रेहती हूँ
कौन से दो नयन मैं उधार लाऊँ
जहाँ मेरी इस उपन्यास को
सच्चाई की एक दुकान मिले
मैं अब भी हिम्मत जुटाते रेहती हूँ
मैं अब भी टूटती पंक्तियों को जोडती हूँ
मैं अब भी एक किताब लिखने का हौसला रखती हूँ
बोलो, क्या इसे कोई खरीदेगा??
जीवन के वो बोल समझ पायेगा??
खून की स्याही, से सींचकर रखी इस किताब को
बोलो...क्या कोई अनमोल खरीदार मिलेगा??
जो पन्नों को मेरी तरह उलट-पलट कर
गुलाब के रंग सा मेरी तन्हाई को भर देगा??
चेहलती इस दुनिया में सोचूँ...घबराऊँ.....
नाउम्मीद का अकक्षर मिटाते रेहती हूँ
हाँ, आज भी मैं कोशिश करती रेहती हूँ ...!
जिंदगी के कई रंग और रुप होते हैं और किसी के आने या फिर जाने से भी उन्हीं रंग और रुप में भी परिवर्तन आ जाता है। ऐसे ही एक पल में बीता और अनुभवी चित्रण...इसिलाह की मुंतजी़र
जिंदगी तो हसीन ही है जाना था
परस्तार ने इसे और रंगीन बना दिया
उसकी परस्तिश में ऐसे डूबे हम
किसी परावार ने जैसे परिवाश बना दिया
घंटों बातों में डूबोकर रखना हमें
हर रंग में ढलते मोज्जाऐं जैसे दिलकश बना दिया
पलभर की खामोशी जैसे मुज़तारिब कर गई
हमको तो दिवानगी में मुफक्किर बना दिया
इस कद्र मेहाव हैं तेरी बातों में जाना
के हमें सब से मेहरूम बना दिया
तसनिफ हमें आ गई
तसनिफ हमें आ गई -छोटा मुहँ बडी़ बात लेकिन ये हौसला मुझे मेरे चाहने वालों से मिला है। इसिलाह की मुंतजी़र
तुम से तो जैसे मैं कल ही मिली थी
फिर कैसे ये दिल की कली खिल गई?
मैंने तो चँद लम्हें ही गुज़ारे थे
किस घडी़ क्या हुआ, दिल की गिरह खुल गई
गुफ्तगू में तुम से तो मैं संभली हुई थी
फिर किन इशारों से आँखें जु़बान बन गई
चँद लम्हों की बातें तसकिन बन गईं
ऐसी जादुगरी की, तसलिम हमारी मिल गई
दूर हुँ तुम से कोसों दूर अकेली
तस्वीर तुम्हारी मुझे राहत दे गई
क्यों मैं करने लगी मुहब्बत तुम से
यही परेशानी एक मेरी रेह गई
कुछ भी केह लो, यही मैंने जाना सनम
दिल तुम्हारा हो गया, मैं पराई रेह गई
देख लो प्यार में हम गाफि़ल रेह गये
कुछ भी केह लो तसनिफ हमें आ गई ;)
पेहली नज़र का धोखा
धोखा अकसर हो जाता है, कभी नादानी में तो कभी अंजाने में... जो भी हो धोखा तो धोखा है.... :)
पेहली नज़र में दिल का खोना
जा़लिम ये किस कदर का धोखा
बातें ही मुसलसल हुईं थीं
फिर खत्म हुआ सब्र दिल का
जा़लिम ने चल दिया अपनी चाल
रेह गया दिल अब स्रिफ रफि़क का
रफ्ता-रफ्ता दिल करने लगा इक़रार
अब तो जैसे रकि़ब हुआ है मेरा हाल
उस से इज़हार-ए-मुहब्बत में
रक्स-ए-ता-उस दिल हुआ जाता
रग-ए-जान में मेरे जैसे तुम बसे हो
रघ़बत सी अनंजुमन में कोई बस जाता
औफिस केक्युबिकल से....
अक्सर बचपन में आधुनिक कवियों की कविताओं में अँग्रेज़ी शब्दों का प्रयोग देखा है, और आज औफिस में बैठकर
जब कुछ पल अपने साथ बिताया तो अनायास ये इच्छा पुरी होती नज़र आई! ज्यादा कुछ यहाँ कहे बगैर आगे का
ब्यौरा नीचे लिखित शब्दों में... चित्रकारी स्वयं फिजा़ के हाथों....;)... किसी भी गुस्ताखी़ के लिऐ पेहले से ही खे़द है।
दिल बेचैन सा है,
खाली वक्त है
और दफ़्तर की मेज़ है।
काम न हो तो भी,
काम जताने की रीत है
जब काम ही न हो
तो भला क्या काम करें
के वक्त कट जाऐ।
ये वक्त काटना भी क्या काम है...!?!
पहाड़ खोदने से न कम है
मेरी असमंजस तो देखो
कभी कंप्युटर स्क्रीन देखूँ
तो कभी सामने रखे
टिशु बौक्स को।
हो न हो इस एकांकीपन में
टिशु बौक्स पर बनी चिडी़या
फूल, पत्ती और उसकी डाली
इन सब से दिल लगा बैठी, ये 'फिजा़'!
उठाया पेंसिल हाथ में
और कर ली चित्रकारी
शुरूआत टिशु पेपर से,
फिर प्रिंटाउट पेपर और
फिर नोट-पैड पर...
यकायक ऐसा लगा
मानो मुझ में अभी है और अरमान
पंछी संग उड़ती पुरवाई
मानो इस दिल ने जाना
फूलों की खुश्बूओं को
जैसे मेहसूस किया
मन विचलित होकर
उड़ने लगा...कहीं दूर
इस औफिस केक्युबिकल से
वहाँ, जहाँ वक्त की
कोई पाबंदियाँ नहीं
तानाशाही भी नहीं।
अपनी चित्रकारी देख
मन स्वयं दाद देने लगा
मानो एक और कला का जन्म हुआ
दिल सोच में फिर घुम होने लगा
क्या मैं एक चित्रकार हुँ?
जिंद़गी इतनी भी बूरी नहीं के
चित्रकारी से गुजा़रा न हो पाऐ...
ऐसे ही कुछ सुनहरे पल
आज औफिस के
क्यूबिकल में बिताऐ।
एक तुम से न हो पाये दूर शाम-ओ-सेहर
इंतजा़र, एक ऐसा अक्षर है जो हर किसी को बेहाल करता है। कई बार असमंजस में डाल देता है तो ....कभी क्रोधित भी...किंतु ...परंतु इंतजा़र हर कोई करता है; चाहे वो बसंत का हो, या नौकरी का या फिर बरखारानी ...इंतजा़र तो भाई! शामो-सेहर होता है। :)
क्या पता था इंतजा़र में हो रहे थे बेखबर
जिसका करते रहे इंतजा़र शाम-ओ-सेहर
चाहत कुछ इस कद्र बढी़ है उनसे के
हर फासले हो रहे ना-कामीयाब शाम-ओ-सेहर
मेरे दिल ने फैसला किया आज उस दिवाने से
कोशिश करेंगे याद करें शाम-ओ-सेहर
किस तरह वादा करें हम याद न करने का
जब भुला ही न पाये हम शाम-ओ-सेहर
गली, शहर सब घुमें 'फिजा़' दूर-दूर
कल से बडी ज़ोरों से बारिश हो रही है...ऐसी घमासान बारिश के बस पूछो नहीं।
मन तो करता है, जैसे निकल पडें बरसात में ऐसे बिना बरसाती और छाते के फिर जो हो सो हो....
बारिश की बूँदें जब
टप-टप करके गिरतीं हैं
कितने सुहाने और मीठे
ऐहसास ये जगातीं है।
मोतियों सी ये बूँदें
मन पर चंचल वार करतीं हैं
आवारा बादल की भाँति
मन, सुहाने पल में खो जाता है।
कितने ही पल में जी उठती हुँ
हर बूँद जब मिट्टी से जा मिलती है
मेरे भी चंचल मन में
इंद्रधनुष सी रंगत भर देतीं हैं।
छोटी-छोटी बूँदों जैसे उनकी बातें
मन के ख्यालों में सौ बीज हैं बोतीं
उन बीजों को सिंचने के
नये-नये हल ढुंढ निकालती।
कब बूँदों जैसे मैं मिल जाऊँ
दरिया के सिने से लग जाऊँ
उन के ही रंग में रंग जाऊँ
कैसा जादू कर देतीं हैं।
सावन के ये बरसाती बूँदें
कहीं हैं ये उमंग लातीं
कहीं ये सुख-चैन ले जातीं
दोनों ही पल सबको सताती।
कुछ मीठे तो कुछ खट्टी यादें
हर एक का मन ललचातीं
ऐसी ही कुछ सपने बुनने
वो कुछ पल हमको दे जातीं।
एक उषा की किरण जैसे
सबके मन में विनोद हैं लातीं
कितने ही सच्चे और मीठे
जीने की हैं राह दिखाते।
जाना! सुबह हो गई...
बहुत दिनों बाद कुछ लिखने की आस जागी, ठीक उसी तरह जिस तरह खेतों में अँकुर खाद, पानी और रवि की किरणों
से प्रज्जवलित हो उठतीं हैं। प्रातःकाल, स्नान लेते वक्त कुछ बातें अकस्मात ही मन कि आँगन में खलबला उठीं...
बातें जो शब्द बनकर ध्यान में विचरण करने लगीं...बस दिल उन्हीं ख्यालों को पिरोने लालायित हो उठा...
इस नाचीज़ की ये एक कृति कुछ इस तरह पेश है....
कल रात कुछ थकीं-थकीं सी थीं
और उनकी बाहों में नींद का आना
उषा की लालिमा चारों ओर फैल चुकीं थीं
फिर भी मैं नींद की
गहराईयों से लिपटी पडी थीं
इतने में उनका आना
मानो एक किरण बनकर
मुझे नींद की गोद से उठाना
और प्यार से केहना -
ये लो कौफी का ये प्याला !
मानो, मेरी सुबह रोशन हो गई
उनके प्यार की खुश्बू
मेरे दिन को मेहका गई
मैंने धीरे से पलकों के किवाड़ों को
खोलने की कोशिश की...
मानो, दिल और नींद की असमंजस में
और इसी द्वंद में फँसी रही...
आज भी नींद की खुश्क वादियों में
फि़जा़ बनकर मेहकती रही..
प्रकृति में बारिश कभी मीठी-मीठी खुशबू या फिर मौसम को रोमांचक बनाती है, तो कभी भारी बरसात से सब कुछ अस्त-व्यस्त हो जाता है। जीवन का संयम भी कभी-कभी ऐसा रूख ले लेता है, कुछ तूफानी बातें तो कुछ मुकाबले की बातें.... आखिरकार जीत लडने वाले और हौसला रखने वाले की ही होती है....
बारिश की बूँदें सर-सर करे बाहर
मेरे दिल में जैसे एक तूफान आये!
बूदों की ज़िद, बिजली की कडकडाहट
तूफानी लेहरों में दिल गोते खाये!
पानी के भवँडर में, मैं धँस गई हुँ
डूबे हैं न निकले, कुछ समझ न आये!
बूँदें बरसकर बेह जातीं हैं
मैं किस ओर बहूँ कोई तो बताये!
तुझ से मिलने की बडी ख़व्वाईश है मुझे
क्या-क्या न पूछूँ और क्या-क्या न तु बताये!
तेरी इस खोखली दुनिया में बस
होली के ऐसे पावन अवसर पर, बचपन बडा याद आता है । पेहले ये सोचकर मन बेहला लेती थी कि अब होली
खेलने नहीं मिलता शायद इस वजह से मन रेह-रेह कर बिते दिनों की याद दिलाता है, किंतु बात ये है कि बचपन पीछा नहीं छोडता...वक्त इस कदर बदल गया है कि
शायद ही वो परंपरा अब तक जिंदा रखी गई हो। एक छोटी सी साधारण सी कविता जिंदगी के रंगों को दर्शाती हुई....
तुम को देखा इंद्रधनुष सा
यादों की तरह वो भी आऐ
कुछ पल रेह कर खुश कर गऐ
यादें ही बन गऐ हैं सहारे
कुछ भी हों, ये हैं जीने के बहाने | hindi |
Jeseniova 124is offering a generously designed studio apartment for sale with an area of 45.28 m² in the sought-after locality of Prague 3 - Žižkov. This west-facing apartment is located on the 1st floor of the building and offers a balcony with an area of 12.3 m².
The Jeseniova 124 project is happy to present this new apartment comprising a spacious living area with space for a kitchenette and access to the balcony, a hall, bathroom equipped with a toilet and a shower cubicle as well as a box room with preparation for a washing machine. A parking space can be purchased to go with the new apartment in Prague 3. The apartment has assigned a cellar. The location of this apartment for sale makes it ideal as a place for you to live or as an advantageous investment.
The fixtures and fittings in the new studio apartment include wooden floor in oak hue and plastic windows with triple-glazing. Ceramic floor and wall tiles will be used in the bathroom.
The project is situated in a pleasant locality which is sought after thanks to its proximity to the centre of Prague and due to the fact that it is undergoing dynamic development, including construction of new residential projects as well as cultural, sports and relaxation centres. Žižkov offers a full range of civic facilities, including nurseries, primary schools, secondary schools and an eight-year grammar school, a wide range of services, shops, restaurants, a club cinema, a post office, a healthcare centre and a pharmacy. Excellent transport links for the new apartments in Prague 3 are provided by tram and bus lines, stops for which are only a couple of minutes' walk from the project. | english |
July 31, 2009 – At 14:33 Station 1 was dispatched along with Cressona Fire Department in the area of 1819 Sweet Arrow Lake Road (North Manheim Township) for a motor vehicle with entrapment and power lines resting on the vehicle. As units arrived on scene, Station 1 requested manpower from Station 4, and Engine 737 hit the roadway.Crews waited for PPL to disconnect the power to the infridging pole and the patient was immediatley extricated. Time out was approximately 1 hour 20 mins.
July 29, 2009- At 20:58 Liberty Station # 4 was dispatched to assist Districts 47, 42, and 56 (Landingville, Deer Lake, and Orwigsburg) on a possible house fire. As Engine 737 and Tanker 738 went repsonding, they were advised that due to a thunderstrom in the area, lightning had struck the house at 3 Main Street, community of Landingville. Incident command Chief 47 (Hoffman) arrived on scene with nothing showing from the exterior, and asked all incoming units to do a search of the inside of the house. Once 737 and 738 arrived on scene, the crews were split up, with one crew searching the third floor and the other in the basement area. After a search with thermal imaging cameras, it was determined that there was no extension into the house from the lightning strike. All units remained on scene for just over 1 hour.
At 18:10, Stations 1 & 4 were dispatched to the area of 141 West Main Street in the borough for a motor vehicle accident with unknown injuries. As units arrived on scene they were met with a single vehicle (Jeep) versus a utility pole and no injuries. Crews applied floor dry, disconnected the vehicles battery, and assisted in cleaning up the debris. Time out was about 35 minutes. ***Thanks to MLK Photos!
July 27, 2009- At 23:14 the Schuylkill Haven Fire Department along with Cressona Fire and Ladder 51, Squad 52 (West End, Pottsville) were dispatched to 1544 Route 61 (The Surgery Center) for an automatic fire alarm. Crews arrived with nothing showing from the exterior and did an investigation of the interior. After about a half hour, it was determined to be a false activation and all unit were cleared.
July 27, 2009- At 08:08 the Schuylkill Haven Fire Department was dispatched to 424 East Union Street, Schuylkill Haven Boro, to assist Medic 63-01 on a cardiac arrest. Crews assisted with packaging the patient and were on scene for about 15 minutes.
July 26, 2009- At 21:19 the Schuylkill Haven RIT was dispatched to 810 North 3rd Street, Pottsville, for a working structure fire. The RIT was dispatched to assist Pottsville as they had a working row home fire. RIT members responded on Engine 737 and Squad 739 with Chief 720 in command. Schuylkill Haven members weren’t utilized but remainded on scene for the better part of 2 hours.
July 23, 2009- MVA at Dock and Center Ave.
July 23, 2009- At 15:36 the S.H.F.D. was dispatched to the intersection of Dock Street and Center Ave, Schuylkill Haven Boro, for a motor vehicle accident. On duty Chief 723 (Donatti) was the first to arrive on location and advised of a 2 car crash with both vehicles still on the roadway with a minor injury. Rescue 727 and Engine 732 arrived on scene and assisted with cleaning debris off the roadway, while Engine 737 went to Center Ave and North Garfield Ave to assist Schuylkill Haven PD with traffic control. All units remained on scene for about 40 minutes.
July 21, 2009- At 21:20 all 3 Schuylkill Haven stations were dispatched to 62 Seven Stars Road, North Manheim Twp, for an automatic fire alarm. However, before any fire apparatus could go responding, the department was cancelled off by the alarm company stating a false activation.
July 19, 2009- At 14:47 Station 1 was dispatched for Rescue 727 and manpower to assist District 34 (Friedensburg & Summit Station) on a search in the area of 1 Hunters Lane, Washington Twp. The initial call was for an off road ATV accident but quickly turned in to a search call as a few people lost their way in the woods. Members from station 1 along with Chief 723 (Donatti) went responding within minutes of dispatch and were quickly activated to assist with the search. In the meantime, more companies were being called to the scene to assist, such as Pine Grove HH&L. Once HH&L was activated, they had station 2 from Schuylkill Haven respond out to their station to cover Pine Grove boro until they returned.The Schuylkill Hose were out in Pine Grove for just over 4.5 hours before being released. Chief 723 and Rescue 727 remained on scene up until after 19:00. All in all, it was a very long and hot day, but thankfully everyone went home!!!
July 16, 2009- At 14:09 stations 2 & 4 were dispatched to 408 Parkway, Schuylkill Haven Boro, for a smoke condition. The two companies were dispatched at the request of Chief 722 (Sattizahn) already on scene for an investigation, with smoke in the basement. Once the two engine companies arrived on scene, they did an investigation with thermal imaging cameras to try to determine the source of the smoke. It was then determined that the smoke was coming from a coal furnace that the homeowner was trying to re-light. Each company was on scene for roughly 20 minutes. | english |
Introduction & Overview on Responsible Data Science: Maarten de Rijke Professor in Information Retrieval, Informatics Institute, UvA.
Martijn van Otterlo AAA Data Science Researcher at Knowledge, Information and Innovation (KIN), Faculty of Economics and Business Administration (FEWEB), Amsterdam Center for Business Analytics (ACBA), VU.
Judith Möller Political Communication & Journalism, Faculty of Social and Behavioural Sciences, UvA.
Mykola Pechenizkiy Full Professor, Chair Data Mining, Department of Computer Science, Eindhoven University of Technology (TU/e), on FAT Predictive Analytics. | english |
'भाभी जी घर पर हैं' की गोरी मैम कान्स में करेंगी शिरकत! | ए२४बॉलिवुड
'भाभी जी घर पर हैं' की गोरी मैम कान्स में करेंगी शिरकत!
मुंबई : टेलीविजन अभिनेत्री सौम्या टंडन ने अपने सीरियल निर्माता से कान्स फिल्म फेस्टिवल में शामिल होने के लिये छुट्टी ले ली है। बता दें कि, वह इस समय एंड टीवी का मशहूर टीवी सीरियल 'भाभी जी घर पर हैं।' में अभिनय कर रही हैं। उनके अभिनय को टेलीविजन के दर्शक बेहद पंसद कर रहे हैं।
जानकारी दें दे कि, सौम्या इसके पहले कान में कभी शामिल नहीं हुई हैं। सौम्या कान को लेकर काफी खुश है। उनका मानना है कि- ' कान्स फेस्टिवल एक ऐसी जगह जहां आपको दुनिया की सभी फिल्म बिरादरी से मिलने और कॉन्टैक्ट बनाने का मौका मिलता है।'
अनीता भाभी ने दे डाली विभूती भैया को धमकी दी!
वैसे, ६९वें कान्स फिल्म महोत्सव में बॉलीवुड के कई मशहूर सितारे ऐश्वर्या राय, सोनम कपूर, रिचा चढ्ढा और नवाजुद्दीन सिद्दीकी शामिल हो चुके हैं। गौरतलब हो कि, इससे पहले बिग बॉस ८ के विनर गौतम गुलाटी पिछले साल कान्स फिल्म फेस्टिवल में दिखाई दिये थे। इस एक्टर ने शॉट फिल्म 'डरपोक' में काम किया था। जिसकी स्क्रीनिंग कान्स में की गई थी। | hindi |
وۄمید چھَم | kashmiri |
تہٕ وؤنُن تَس زِ ژٕ گژھ بازر تہٕ اَن کینٛہہ کھؠنہٕ خٲطرٕ | kashmiri |
राज्य समीक्षा पहाड़ी फल्टू देवभूमि में है दुनिया का सबसे ऊंचा शिव मंदिर..तृतीय केदार के आगे सिर झुकाती है दुनिया
देवभूमि में है दुनिया का सबसे ऊंचा शिव मंदिर..तृतीय केदार के आगे सिर झुकाती है दुनिया
वास्तव में देवभूमि के कण कण में भगवान बसे हैं। यहां तृतीय केदार के रूप में दुनिया का सबसे ऊंचा शिव मंदिर मौजूद है...आइए इस बारे में जानिए
कपिल २१ आग २०१८ पहाड़ी फल्टू
भारत देवभूमि है। यहां करोड़ों देवी देवताओं के प्राचीन मान्यताओं के मंदिर हैं, वहीँ भारत में सबसे ज्यादा पूजे जाने वाले भगवान शिव के बहुत से प्राचीन मंदिर हैं, जहाँ भोले के भक्तों का तांता लगा रहता है, लेकिन आज हम आपको एक इसे शिव मंदिर के बारे में बताने जा रहे हैं, जिसकी गिनती दुनिया के सबसे ऊँचे शिवालय में होती है। करीब ३,६८० मीटर की ऊंचाई पर स्थित इस शिवालय को विश्व का सबसे ऊंचा शिवालय माना जाता है। इस बेहद ही खास सबसे ऊंचा शिवालय देवभूमि उत्तराखंड के रुद्रप्रयाग जिले में स्थित है। इस जिले में तुंगनाथ नामक पहाड़ पर स्थित ये शिवालय तुंगनाथ मंदिर के नाम से मशहूर है। तकरीबन १००० साल पुराना तुंगनाथ मंदिर केदारनाथ और बद्रीनाथ मंदिर के बीचों-बीच स्थित है। इसके अलावा भी इस मंदिर की कई खास बातें हैं।
ग्रेनाइट पत्थरों से निर्मित इस भव्य और प्राचीन मंदिर को देखने के लिए हर साल भारी तादात में तीर्थयात्री और पर्यटक यहां आते हैं। इस मंदिर के निर्माण के बारे में ऐसी मान्यता है कि द्वापर युग में महाभारत के युद्ध के दौरान हुए विशाल नरसंहार के बाद भगवान शिव पांडवों से रूष्ट हो गए थे। तब भगवान शिव की प्रसन्न करने के लिए पांडवों ने इस मंदिर का निर्माण कर उनकी उपासना की थी। इस मंदिर को लेकर एक और मान्यता जुड़ी हुई है। कहा जाता है कि त्रेतायुग में भगवान श्रीराम ने जब रावण का वध किया तब खुद को ब्रह्महत्या के पाप से मुक्त करने के लिये उन्होंने इस स्थान पर आकर भगवान शिव की तपस्या की थी। लेकिन इस ऊंचे शिवालय तक पहुंचना इतना आसान भी नहीं है। तुंगनाथ मंदिर के प्रवेश द्वार पर चोपता की ओर बढ़ते हुए रास्ते में बांस के वृक्षों का घना जंगल और मनोहारी नजारे देखने को मिलते हैं।
यह भी पढें - मां धारी देवी मंदिर जल्द ही भव्य रूप में दिखेगा, मां के नए दरबार की ये तस्वीरें देखिए
चोपता से तुंगनाथ मंदिर की दूरी मात्र तीन किलोमीटर ही रह जाती है। चोपता से तुंगनाथ तक यात्रियों को पैदल ही सफर तय करना होता है। इस दौरान भगवान शिव के कई प्राचीन मंदिरों के दर्शन भी होते हैं। आपको बता दें कि हर साल नवंबर और मार्च के बीच के समय में यह मंदिर बर्फबारी के कारण बंद रहता है। लकिन जब आम भक्तों के लिए इस मंदिर के कपाट खुलते हैं तो यहां भक्तों का तांता लग जाता है। तुंगनाथ-चोपता-रांसी ट्रैक को बेहतरीन कहा जाता है। चोपता से शुरु होकर इस ट्रैक में कई दिन हरे भरे घास के बुग्यालों, जंगलों से होकर हिमालय की बायोडायवर्सिटी का दीदार होता है। चोपता-तुंगनाथ को मिनी स्विटजरलैंड भी कहा गया है। इस ट्रैक की शुरुआत चोपता से होती है. चोपता के छोटे छोटे मखमली बुग्याल जो चारों और से बांज, बुरांश, देवदार, कैल के पेडों से घिरे हैं। चोपता से पाली बुग्याल होते हुए थौली में पहला पडाव खत्म होता है। थौली से फिर बिसुडी ताल पड़ता है जो बेहद सुन्दर ताल है। बिसुडी ताल से बनतोली होते हुए रांसी पड़ता है। इस ट्रैक को पंचकेदार ट्रैक के नाम से भी जाना जाता है।
उत्तराखंड के ५ जिलों में इंटरनेट ठप कर दिया, पहाड़ में अघोषित आपातकाल- 'रमेश पहाड़ी'प्रेवियस पोस्ट
देवभूमि लाई जाएंगी अटल जी की अस्थियां, पहाड़ की इन पवित्र नदियों में होगा विसर्जननेक्स्ट पोस्ट | hindi |
Moderate or heavy rain shower Thursday, temperatures as high as 14°C / 58°F, low temperature around 5°C / 41°F, probability of precipitation 79%, wind out of the ESE 10 km/h / 6 mph. Barometric pressure 1016 mb / 30 in, visibility 17 km / 11 mi, humidity 71%.
Patchy rain possible Friday, temperatures as high as 13°C / 55°F, low temperature around 6°C / 43°F, probability of precipitation 82%, wind out of the ESE 11 km/h / 7 mph. Barometric pressure 1016 mb / 30 in, visibility 16 km / 10 mi, humidity 73%.
Patchy rain possible Saturday, temperatures as high as 14°C / 57°F, low temperature around 6°C / 43°F, probability of precipitation 73%, wind out of the ENE 9 km/h / 5 mph. Barometric pressure 1016 mb / 30 in, visibility 16 km / 10 mi, humidity 70%.
Moderate or heavy rain shower Sunday, temperatures as high as 15°C / 59°F, low temperature around 5°C / 42°F, probability of precipitation 68%, wind out of the SSW 7 km/h / 4 mph. Barometric pressure 1014 mb / 29.94 in, visibility 16 km / 10 mi, humidity 66%.
Moderate or heavy rain shower Monday, temperatures as high as 13°C / 56°F, low temperature around 6°C / 42°F, probability of precipitation 88%, wind out of the E 13 km/h / 8 mph. Barometric pressure 1015 mb / 29.97 in, visibility 15 km / 9 mi, humidity 70%.
Moderate rain at times Tuesday, temperatures as high as 14°C / 56°F, low temperature around 5°C / 42°F, probability of precipitation 86%, wind out of the E 10 km/h / 6 mph. Barometric pressure 1017 mb / 30.03 in, visibility 13 km / 8 mi, humidity 73%.
Moderate rain at times Wednesday, temperatures as high as 13°C / 56°F, low temperature around 5°C / 41°F, probability of precipitation 82%, wind out of the ENE 12 km/h / 7 mph. Barometric pressure 1018 mb / 30.06 in, visibility 16 km / 10 mi, humidity 69%.
La Paz, Bolivia Weather Forecast - Find local La Paz, Bolivia weather forecast and current conditions. Continually striving to be your best resource for Local La Paz, Bolivia Weather! | english |
تیمِہ حِصاب چھ اگر ہے داشیگام نیشنل پارک چھ بناونہ آمژن تِہندِ پاپتھن سُہ ہسا گژِھ آسٕنِہ مطلب<GARBAGE> فار اِکزامپل | kashmiri |
We chat with our recently recruited Data Strategy Director, Alistair McCall, who brings a wealth of knowledge that spans over decade in data and analytics. Originally from Scotland, Alistair has found his home down under and has worked with heavy hitters like Woolworth’s and Optus.
He touches on how he brings data-driven thinking into a creative agency and shares insight on predictive analytics along with the challenges and opportunities that lie ahead.
Hey Al – so you’re our Data Strategy Director, what does that mean?
I look after the data capability here at MercerBell. Together with a highly skilled team of analysts, we do great data analytics work for our existing clients. My role consists of leading and developing the team, all while liaising with existing data clients to help guide them through their challenges and opportunities. I also work with new clients to find ways where we can use our expertise to help them realise their opportunities, leverage their data and stay one step ahead.
Your accent tells me you’re not originally from here. What brought you to MercerBell?
Well, I’m originally from Scotland but I’ve lived in Sydney for the last 18 years. I may never lose my Scottish accent, but I consider myself a proper Aussie!
In terms of career, over the last ten years I’ve worked client side in data and analytics for some large organisations; most recently Woolworth’s, and prior to that, in the telco industry for Optus and then Vodafone.
At Woolworth’s Liquor Group, I developed an analytics capability for several different direct to consumer liquor retailers under the Woolworth’s umbrella. We worked with data in all different shapes and sizes to develop reporting, customer insights and advanced analytics solutions – basically any way that we could use the huge amounts of data available to us to improve our understanding of our customers, and ultimately provide our customers with a high quality experience each time that they interacted with us.
So the opportunity to work for a leading agency in CRM and customer experience like MercerBell, felt like a great opportunity to continue to grow my career in this space, while also giving me a new perspective and fresh challenge on the agency side.
We’ve heard that predictive analytics can help improve customer experience. Can you shed some light on what it is and your experience using it?
Put simply, predictive analytics is a form of advanced analytics that uses data to anticipate outcomes and behaviours that may happen in the future. These predictions are based on both current trends and historical facts; data is analysed with machine learning and data mining to make the most accurate predictions possible.
It’s been around for a long time, although it has become prevalent of late as computers have become more powerful, software has become more user friendly, and data has become so much more abundant.
Consequently, organisations look to their data to provide them with a means of competitive advantage. Organisations use predictive analytics in a number of different ways, including marketing optimisation and CRM, fraud detection, credit scoring and health care.
Churn models use historical transactions to detect changes in shopper behaviour which is a strong indicator of future disengagement. Armed with this advanced knowledge, marketing efforts can be directed at these high-risk customers to reduce the chances of attrition.
Predicting the way in which certain groups of customers are most likely to interact with a brand helps to optimise the timing and marketing channel used by retailers. For example, would you believe that there are a significant group of Australians who are happy to buy wine over the phone at 10am on a Monday morning?
What’s it like to do data at Mercerbell?
It’s fantastic to have the opportunity to work with such a variety of clients, across so many different industries. However, despite these differences, many of the data related challenges organisations face are similar, so my challenge is to get my foot in all of these different doors and demonstrate how MercerBell can help.
Organisations that are successful in transforming their approach to marketing & customer experience with data think big but start small – the first step is to select the right use case which will give quick demonstrable returns if successful.
True 1-1 marketing with the right content being delivered in the right context to an individual regardless of touchpoint is now achievable for any organisation committed to making the right investment in data and technology.
Machine learning and AI will continue to enter the mainstream as more tools and practical applications become available.
MercerBell is proud to welcome Alistair McCall to the team. His appointment is a clear demonstration of our readiness to innovate as we improve the way we deliver more delightful customer experiences. | english |
\begin{document}
\title{Two-state teleportation}
\author{L. Henderson, L. Hardy and V. Vedral\\Centre for Quantum Computation, Clarendon Laboratory, University of Oxford,\\Parks Road OX1 3PU}
\date{\today}
\maketitle
\begin{abstract}
Quantum teleportation with additional a priori information about the input
state achieves higher fidelity than teleportation of a completely unknown
state. However, perfect teleportation of two non-orthogonal input states
requires the same amount of entanglement as perfect teleportation of an
unknown state, namely one ebit. We analyse how well two-state teleportation
can be achieved using every degree of pure-state entanglement. We find the
highest fidelity of `teleportation' that can be achieved with only classical
communication but no shared entanglement. A two-state telecloning scheme is constructed.
\end{abstract}
\section{Introduction}
Transmission of quantum states can be accomplished either by direct sending of
qubits, or by transmission of classical bits where the sender and receiver
share entanglement. In schemes for quantum teleportation it has been shown
that the transmission of two classical bits together with the use of one ebit
achieves the same results as sending one qubit, \cite{Bennett93}.
If the state to be teleported is completely unknown, the fact that the amount
of entanglement between two separated subsystems may not increase under local
operations means that faithful teleportation cannot be achieved without one
full unit of entanglement. The argument goes as follows. Alice's particle is
initially in an unknown state, which could be a mixed state due to
entanglement with another particle $R$ at Alice's end. After the
teleportation, the entanglement between Alice's particle and $R$ is
transferred to an entanglement between Bob's particle and $R$, by entanglement
swapping, \cite{Zukowski93}. The original entangled channel between Alice and
Bob is completely destroyed. Local operations and classical communication
cannot increase the entanglement between Alice and Bob. Therefore the original
entanglement in the channel must be at least as high as the final entanglement
between Bob's particle and $R$. However the initial state of Alice's particle
is completely unknown, it may be a maximally mixed state, arising because
Alice's particle is maximally entangled to another particle, $R$. This would
make the final entanglement between Bob and $R$ maximal. Therefore the initial
entanglement in the channel must be maximal also, \cite{Plenio98}.
On the other hand, if Alice knows exactly what state she has, there is no need
for any entanglement to reliably transmit the state. She simply sends Bob
classical information saying which state it is, and he prepares it himself.
Between the two extremes of Alice possessing no prior information of the
state, and Alice possessing full information, she may have some prior
knowledge. For example, she may receive her qubits from a known ensemble
$\varepsilon=\{\left| \phi_{x}\right\rangle ,p_{x}\}$ of states $\left|
\phi_{x}\right\rangle $ with probability $p_{x}$.We consider the situation
where Alice knows that a preparer of quantum states provides her with one of
two non-orthogonal states, say $\left| \psi_{1}\right\rangle $ $=\cos
(\frac{\theta}{2})\left| 0\right\rangle +\sin(\frac{\theta}{2})\left|
1\right\rangle $ and $\left| \psi_{2}\right\rangle $ $=\sin(\frac{\theta}
{2})\left| 0\right\rangle +\cos(\frac{\theta}{2})\left| 1\right\rangle $
with equal probabilities. Alice then knows almost everything about the state.
In effect she has to transmit one bit of information to Bob saying which of
the two states she has. Is it possible to teleport the quantum state in this
case, using less than the full unit of entanglement required when the state is
completely unknown?
It turns out, rather surprisingly, that it is not possible and that a full
unit of entanglement is needed even for teleportation of only two states. This
is shown in section \ref{sec:ent}. In section \ref{sec:class}, we find the
upper bound for the fidelity of sending the state with no entanglement. In
section \ref{sec:methods}, we consider teleportation using a non-maximally
entangled channel. We make some connections between teleportation and cloning
in section \ref{sec:cloning}, and adapt the telecloning scheme of Murao
\textit{et al.}, \cite{Murao99}, to the case of telecloning two non-orthogonal
states. The two-state telecloning state is now different from that for
universal telecloning. We find that the amount of entanglement required
between sender and recipients is now state-dependent.
\section{Schemes without \label{sec:class}entanglement}
For comparison, we first determine what fidelity of transmission can be
achieved without using any entanglement, only classical communication. Alice
measures her state and sends the result to Bob, who makes his best guess of
the state based on this information. The fidelity of sending the state
$\left| \psi\right\rangle $ is defined as
\begin{equation}
F_{cl}(\left| \psi\right\rangle )=\sum_{i=1}^{n}P(i|\psi)|\langle\psi
|\alpha_{i}\rangle|^{2} \label{eq:fid}
\end{equation}
where $P(i|\psi)=$ $\langle\psi|A_{i}\left| \psi\right\rangle $ is the
probability of Alice obtaining the result corresponding to the positive
operator $A_{i}$ out of $n$ possible outcomes of the POVM $\{A_{i}\}$ where
$\sum_{i=1}^{n}A_{i}=1$. The state $|\alpha_{i}\rangle$ is Bob's guess, given
outcome $i$.
When the input state is completely unknown, the average of the fidelity over
an even distribution of all states on the Bloch sphere is taken. It has been
shown that the average fidelity over all states is \cite{Massar95}
\begin{align*}
F_{cl} & =\int\sum_{i=1}^{n}P(i|\psi)|\langle\psi|\alpha_{i}\rangle
|^{2})d\Omega\\
& =\frac{2}{3}
\end{align*}
In this case, Alice may make an orthogonal measurement in any direction, and
it is optimal for Bob to prepare the state corresponding to Alice's result.
On the other hand, when Alice's state is drawn from an ensemble of two states,
$\{\left| \psi_{1}\right\rangle ,\left| \psi_{2}\right\rangle \}$ with equal
probabilities, the fidelity
\[
F_{cl}(\{\left| \psi_{1}\right\rangle ,\left| \psi_{2}\right\rangle
\})=\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{2}P(i|\psi_{j})|\langle\psi
_{j}|\alpha_{i}\rangle|^{2}
\]
is much higher. This is the case we consider in this paper.
We first calculate the fidelity in the case where Bob simply prepares a
guessed state corresponding to one of the two input states, $\left|
\alpha_{i}\right\rangle \in\{\left| \psi_{1}\right\rangle ,\left| \psi
_{2}\right\rangle $ $\}$, for all $i=1...n$. Then the fidelity is limited only
by the errors Alice makes in measuring, due to the fact that the signal states
are non-orthogonal. We employ previous results on distinguishing two states.
These results have been derived with respect to two different ways of
characterising distinguishability. The states may either be distinguished so
as to minimise the probability of error in guessing the right state, or by
using an `unambiguous' measurement, which has no probability of error, but
which sometimes yields no information about the state.
It has been shown, \cite{Helstrom76}, that the smallest attainable probability
of error in distinguishing two states is
\[
P_{e}=\frac{1}{2}-\frac{1}{4}Tr(\left| \rho_{1}-\rho_{0}\right| )
\]
For two pure states $\left| \psi_{1}\right\rangle $ and $\left| \psi
_{2}\right\rangle $, the minimal probability of error may be derived from the
unitary evolution of the unknown state and an ancilla qubit, initially in the
state $\left| 0\right\rangle _{A}$, on which a projective measurement will be
performed in the $\{\left| 0\right\rangle ,\left| 1\right\rangle \}$ basis:
\begin{align}
\left| 0\right\rangle _{A}\left| \psi_{1}\right\rangle & \rightarrow
\sqrt{1-P_{e}}\left| 0\right\rangle _{A}\left| \psi_{1}\right\rangle
+\sqrt{P_{e}}\left| 1\right\rangle _{A}\left| \psi_{2}\right\rangle
\label{eq:unit}\\
\left| 0\right\rangle _{A}\left| \psi_{2}\right\rangle & \rightarrow
\sqrt{P_{e}}\left| 0\right\rangle _{A}\left| \psi_{1}\right\rangle
+\sqrt{1-P_{e}}\left| 1\right\rangle _{A}\left| \psi_{2}\right\rangle
\nonumber
\end{align}
If the ancilla is measured in the state $\left| 0\right\rangle _{A}$, we
conclude the state is $\left| \psi_{1}\right\rangle $ and if \ $\left|
1\right\rangle _{A}$, then we conclude $\left| \psi_{2}\right\rangle $. The
requirement that this evolution be unitary gives
\[
P_{e}=\frac{1}{2}(1\pm\sqrt{1-|\langle\psi_{1}|\psi_{2}\rangle|^{2}})
\]
For two pure states $\left| \psi_{1}\right\rangle $ $=\cos\frac{\theta}
{2}\left| 0\right\rangle +\sin\frac{\theta}{2}\left| 1\right\rangle $ and
$\left| \psi_{2}\right\rangle $ $=\sin\frac{\theta}{2}\left| 0\right\rangle
+\cos\frac{\theta}{2}\left| 1\right\rangle ,$ this is given by
\begin{equation}
P_{e}=\frac{1}{2}(1-\cos\theta)\nonumber
\end{equation}
If $\theta=0$, the two states are orthogonal and the probability of error is
zero. If no error is made, Bob prepares Alice's state with perfect fidelity.
If Alice makes an error, there is still some overlap with the correct state,
given by $\sin^{2}\theta$. The fidelity is therefore
\begin{align}
F & =(1-P_{e}).1+P_{e}\sin^{2}\theta\label{eq:minprob}\\
& =1-\frac{1}{2}(1-\cos\theta)\cos^{2}\theta\nonumber
\end{align}
For orthogonal states, $\theta=0$, $F_{1}=1$. For maximally non-orthogonal
states with $\theta=\frac{\pi}{4}$, $F_{1}=0.927.$
An alternative strategy is to construct a POVM which distinguishes the two
outcomes, $\left| \psi_{1}\right\rangle $ and $\left| \psi_{2}\right\rangle
$, with no probability of error, but has a third outcome where the state is
completely unknown. Then the maximum probability of a successful outcome is
\cite{Ivanovic87}, \cite{Dieks88}, \cite{Peres88} \label{eq:probsuccess}which
is $P_{s}=1-\sin\theta$ in our case.
\begin{figure}
\caption{Fidelity when Bob guesses one of the two input states. The solid line
corresponds to the measurement which minimises Alice's probability of error,
Eq. (\ref{eq:minprob}
\label{fig1}
\end{figure}
If the `don't know' outcome is obtained, Bob chooses at random which state to
prepare. In half the cases, he succeeds. If he fails, there is still an
overlap with the correct state. Therefore the fidelity is
\begin{equation}
F=1-\frac{1}{2}\sin\theta+\frac{1}{2}\sin^{3}\theta\label{eq:unamb}
\end{equation}
This fidelity is always lower than that achieved by minimising the probability
of error, (see Fig. (\ref{fig1})).
However the strategy where Alice minimises her probability of error and Bob
prepares one of the input states is not optimal. It is possible to achieve a
higher fidelity if Bob prepares a guess which has a slightly higher overlap
with the other state to take into account the possibility that Alice makes an
error. Alice still makes the measurement which minimises her probability of
error. For the two states $\left| \psi_{1}\right\rangle $ $=\cos(\frac
{\theta}{2})\left| 0\right\rangle +\sin(\frac{\theta}{2})\left|
1\right\rangle $ and $\left| \psi_{2}\right\rangle $ $=\sin(\frac{\theta}
{2})\left| 0\right\rangle +\cos(\frac{\theta}{2})\left| 1\right\rangle $
this is a projection onto $\left| 0\right\rangle $ or $\left| 1\right\rangle
$. The positive operators of the POVM to be performed are $A_{1}=\left|
0\right\rangle \langle0|$ and $A_{2}=\left| 1\right\rangle \langle1|$ and the
corresponding probabilities are
\begin{align*}
p(1|\psi_{1}) & =|\left\langle 0|\psi_{1}\right\rangle |^{2}=\cos^{2}
(\frac{\theta}{2})\\
p(2|\psi_{1}) & =|\left\langle 1|\psi_{1}\right\rangle |^{2}=\sin^{2}
(\frac{\theta}{2})\\
p(1|\psi_{2}) & =|\left\langle 0|\psi_{2}\right\rangle |^{2}=\sin^{2}
(\frac{\theta}{2})\\
p(2|\psi_{2}) & =|\left\langle 0|\psi_{2}\right\rangle |^{2}=\cos^{2}
(\frac{\theta}{2})
\end{align*}
The fidelity is
\begin{align*}
F_{cl} & =\frac{1}{2}(p(1|\psi_{1})|\left\langle \alpha|\psi_{1}
\right\rangle |^{2}+p(2|\psi_{1})|\left\langle \beta|\psi_{1}\right\rangle
|^{2}\\
& +p(1|\psi_{2})|\left\langle \alpha|\psi_{2}\right\rangle |^{2}+p(2|\psi
_{2})|\left\langle \beta|\psi_{2}\right\rangle |^{2})
\end{align*}
where $\left| \alpha\right\rangle $ and $\left| \beta\right\rangle $ are
Bob's guessed states. Assuming that the fidelity must be the same under
interchange of the two states, and that the guessed states share the same
symmetry as the input states, so that $|\left\langle \alpha|\psi
_{1}\right\rangle |^{2}=|\left\langle \beta|\psi_{2}\right\rangle |^{2}$, and
$|\left\langle \beta|\psi_{1}\right\rangle |^{2}=|\left\langle \alpha|\psi
_{2}\right\rangle |^{2}$, the fidelity becomes
\begin{align}
F_{cl} & =p(1|\psi_{1})|\left\langle \alpha|\psi_{1}\right\rangle
|^{2}+p(2|\psi_{1})|\left\langle \beta|\psi_{1}\right\rangle |^{2}
\label{eq:fidtwo}\\
& =\cos^{2}\frac{\theta}{2}\cos^{2}(\frac{\theta-\alpha}{2})+\sin^{2}
\frac{\theta}{2}\sin^{2}(\frac{\theta+\alpha}{2})\nonumber
\end{align}
Differentiating with respect to the choice of guessed angle $\alpha$ gives
\[
\frac{\partial F_{cl}}{\partial\alpha}=p(1|\psi_{1})\sin(\theta-\alpha
)+p(2|\psi_{1})\sin(\theta+\alpha)
\]
We find the maximum value of $F_{cl}$ by setting $\frac{\partial F_{cl}
}{\partial\alpha}=0$. The angle which gives a maximum is
\[
\alpha=\tan^{-1}\left( \frac{\sin\theta}{\cos^{2}\theta}\right)
\]
Substituting into Eq. (\ref{eq:fidtwo}) gives the fidelity plotted in Fig.
(\ref{fig2}). Notice that this fidelity, unlike the fidelity of the other
strategies, is symmetrical about $\theta=\frac{\pi}{4}$.
\begin{figure}
\caption{Fidelity when Alice minimises her probability of error. The dashed
line shows the case where Bob prepares the state she specifies, Eq.
(\ref{eq:minprob}
\label{fig2}
\end{figure}
This result coincides with the following expression derived by Fuchs and
Peres, \cite{Fuchs95}, in the context of eavesdropping,
\[
F_{cl}=\frac{1}{2}(1+\sqrt{1-|\langle\psi_{1}|\psi_{2}\rangle|^{2}
+|\langle\psi_{1}|\psi_{2}\rangle|^{4}})
\]
In this scenario, Alice tries to communicate to Bob one of a set of
non-orthogonal states, which is intercepted by Eve. Eve wants to extract as
much information as possible from a measurement on the state, and at the same
time to prepare a new state with as high fidelity as possible with Alice's
original state so as to deceive Bob. Eve performs the dual function of Alice
as measurer and Bob as preparer in our scheme where Alice and Bob are
connected only by a classical channel. It is plausible that for Bob to
maximise the fidelity, he should have maximum information about the state and
that Alice should also maximise her information by making the measurement
which minimises the probability of error. This suggests that the fidelity of
Eq. (\ref{eq:fidtwo})\ is optimal. The symmetry about $\theta=\frac{\pi}{4}$
may indicate optimality since all the less efficient strategies that we
investigated do not possess this symmetry. Fuchs and Peres give further
numerical and plausibility arguments in support of the optimality of this fidelity.
Up till now the discussion has focussed on the situation where Alice and Bob
communicate only by a classical channel. We now consider how shared
entanglement can improve the fidelity of teleportation.
\section{Use of entanglement\label{sec:ent}}
If Alice and Bob share only one entangled pair, perfect two-state
teleportation cannot be achieved without a full unit of entanglement. By
contrast, in the asymptotic case with many copies of the state and many
entangled pairs, perfect teleportation may be achieved with less than one full
unit of entanglement for each qubit communicated.
\subsection{Single channel case\label{sect:single}}
We prove that it is not possible to teleport perfectly with less than one full
unit of entanglement, even if the state to be teleported comes from a known
ensemble of only two non-orthogonal states. Let the state to be teleported be
$\left| \phi\right\rangle _{1}$, and the entangled channel $\left|
\psi\right\rangle _{23}$. Then the initial state of the three particles may be
written as
\[
\left| \phi\right\rangle _{1}\left| \psi\right\rangle _{23}=\sum_{k}
c_{k}^{\phi}\left| k\right\rangle _{12}U_{k}^{-1}\left| \phi\right\rangle
_{3}
\]
where the coefficient $c_{k}^{\phi}$ may depend on the initial state $\phi$.
The state has been expanded as a bipartite decomposition of the first two
particles versus the third, where the orthonormal basis of the first two
particles is given by $\{\left| k\right\rangle _{12}\}$ and the corresponding
states of the third particle are $U_{k}^{-1}\left| \phi\right\rangle _{3}$,
not necessarily orthogonal. Any general teleportation scheme must be of this
form. The state can be transformed unitarily as
\begin{equation}
U(\left| \phi\right\rangle _{1}\left| \psi\right\rangle _{23})=(\sum
_{k}c_{k}^{\phi}\left| k\right\rangle _{12})\left| \phi\right\rangle _{3}
\end{equation}
by the controlled unitary operation $U_{k}$ on the third particle. Let
$|A(\phi)\rangle_{12}=(\sum_{k}c_{k}^{\phi}\left| k\right\rangle _{12})$ and
consider two input states, $\left| \phi\right\rangle $ and $\left|
\phi^{\prime}\right\rangle $. By taking the overlap of Eq. (\ref{eq:unit})
with a similar equation for $\left| \phi^{\prime}\right\rangle $, we obtain
\[
_{1}\langle\phi^{\prime}\left| \phi\right\rangle _{1}=(_{12}\langle
A(\phi^{\prime})|A(\phi)\rangle_{12})(_{3}\langle\phi^{\prime}\left|
\phi\right\rangle _{3})
\]
Since
\[
_{1}\langle\phi^{\prime}\left| \phi\right\rangle _{1}=_{3}\langle\phi
^{\prime}\left| \phi\right\rangle _{3}
\]
it follows that either $\langle\phi^{\prime}\left| \phi\right\rangle =0$, or
$_{12}\langle A(\phi^{\prime})|A(\phi)\rangle_{12}=1$. If $\ \langle
\phi^{\prime}\left| \phi\right\rangle =0$, the two input states are
orthogonal and perfect teleportation can be achieved without the use of any
entanglement at all, since an exact measurement to distinguish the states can
be performed. The vectors $\left| A(\phi)\right\rangle _{12}$ and $\left|
A(\phi^{\prime})\right\rangle _{12}$ are normalised. Hence, if $_{12}\langle
A(\phi^{\prime})|A(\phi)\rangle_{12}=1$, then $\left| A(\phi)\right\rangle
_{12}=$ $\left| A(\phi^{\prime})\right\rangle _{12}$ and consequently the
coefficients $c_{k}^{\phi}$ must be independent of the input state $\phi$, so
that $c_{k}^{\phi}=c_{k}^{\phi^{\prime}}$. Therefore the probability of
obtaining the result $k$ is independent of the input state.
Any state to be teleported can be written as a linear combination of the
states $\left| \phi\right\rangle $ and $\left| \phi^{\prime}\right\rangle $
\[
\left| \psi\right\rangle =a\left| \phi\right\rangle +b\left| \phi^{\prime
}\right\rangle
\]
If both $\left| \phi\right\rangle $ and $\left| \phi^{\prime}\right\rangle $
can be teleported perfectly by the same operation, there exists a unitary
transformation $U$ such that
\[
U(\left| \phi\right\rangle _{1}\left| \psi\right\rangle _{23})=(\sum
_{k}c_{k}\left| k\right\rangle _{12})\left| \phi\right\rangle _{3}
\]
and
\[
U(\left| \phi^{\prime}\right\rangle _{1}\left| \psi\right\rangle
_{23})=(\sum_{k}c_{k}\left| k\right\rangle _{12})\left| \phi^{\prime
}\right\rangle _{3}
\]
where we have shown that the coefficients $c_{k}$ do not depend on the input
state. Therefore
\[
U(a\left| \phi\right\rangle _{1}+b\left| \phi^{\prime}\right\rangle
_{1})\left| \psi\right\rangle _{23}=\sum_{k}c_{k}\left| k\right\rangle
_{12}(a\left| \phi\right\rangle _{3}+b\left| \phi^{\prime}\right\rangle
_{3})
\]
and so any state can be teleported perfectly. This would mean it were possible
to perfectly teleport a maximally mixed state. By the arguments of the
introduction this would require a full unit of entanglement.
\subsection{Asymptotic case\label{sec:asymp}}
Alice's qubit is an equally weighted mixture of the two possible input states
and so can be described by the density matrix
\[
\rho=\frac{1}{2}(\left| \psi_{1}\right\rangle \langle\psi_{1}|+\left|
\psi_{2}\right\rangle \langle\psi_{2}|)
\]
Now if Alice possesses a large number $n$ of copies of the qubit, she may use
Schumacher compression, \cite{Schumacher95}, to compress the same information
into $nS(\rho)$ qubits, where $S(\rho)=-tr(\rho\log\rho)$ is the Von Neumann
entropy of the qubit $\rho$. If $\theta=0$, and the two states are orthogonal,
$S(\rho)=\log2=1$. \ This is the only case where no compression is possible.
For two maximally non-orthogonal states, with $\theta=\frac{\pi}{4}$,
$S(\rho)\approx0.907$ and transmission requires $0.907$ ebits per qubit of information.
If Alice and Bob share a large number $m$ of non-maximally entangled pairs in
the state $\rho_{AB}$, with $\rho_{A}=Tr_{B}(\rho_{AB})$, they may distill
$mS(\rho_{A})$ maximally entangled pairs using only local operations and
classical communication, \cite{Bennett96},\cite{Bennett96prl}. The quantity
$S(\rho_{A})$ denotes the amount of entanglement in the shared pairs and for a
maximally entangled state, $S(\rho_{A})=1$. The amount of entanglement
$S(\rho_{A})$ required per qubit of information sent by Alice is $S(\rho
_{A})=\frac{n}{m}S(\rho)$, which may be less than one in the limit of large
$m$ and $n$, when the input states are non-orthogonal. Clearly then, the
asymptotic case is different from the situation where only single copies of
the states are available.
\section{Teleportation through a non-maximally entangled
channel\label{sec:methods}}
Given that when Alice and Bob share only one non-maximally entangled channel
it is not possible to perform two-state teleportation perfectly, we would like
to know how high a fidelity can be achieved. Below, we compare several
different strategies, however it is still an open question what the most
optimal scheme would be.
If we apply the standard teleportation procedure, sending the initial state
\[
\left| \psi\right\rangle _{1}=\cos\frac{\theta}{2}\left| 0\right\rangle
+\sin\frac{\theta}{2}\exp(i\phi)\left| 1\right\rangle
\]
through the non-maximally entangled channel
\[
\left| \psi\right\rangle _{23}=\alpha\left| 00\right\rangle +\beta\left|
11\right\rangle
\]
then the initial state of the three particles may be written as
\begin{align}
\left| \psi\right\rangle _{123} & =\frac{1}{\sqrt{2}}(\left| \phi
^{+}\right\rangle (\alpha\cos\frac{\theta}{2}\left| 0\right\rangle +\beta
\sin\frac{\theta}{2}e^{i\phi}\left| 1\right\rangle )\label{eq:bellbasis}\\
& +\left| \phi^{-}\right\rangle (\alpha\cos\frac{\theta}{2}\left|
0\right\rangle -\beta\sin\frac{\theta}{2}e^{i\phi}\left| 1\right\rangle
)\nonumber\\
& +\left| \psi^{+}\right\rangle (\alpha\sin\frac{\theta}{2}e^{i\phi}\left|
0\right\rangle +\beta\cos\frac{\theta}{2}\left| 1\right\rangle )\nonumber\\
& +\left| \psi^{-}\right\rangle (-\alpha\sin\frac{\theta}{2}e^{i\phi}\left|
0\right\rangle +\beta\cos\frac{\theta}{2}\left| 1\right\rangle ))\nonumber
\end{align}
Without loss of generality, we assume that $\alpha$ and $\beta$ are real and
that $\alpha\leq\beta$. The fidelity is given by
\[
F(\left| \psi\right\rangle )=\sum_{i=1}^{4}p(i|\psi)|\left\langle \psi
|\alpha_{i}\right\rangle |^{2}
\]
where $i$ is the index of the projections $A_{i}=\left| \phi_{i}\right\rangle
\langle\phi_{i}|$ onto the four Bell states
\begin{align*}
\left| \phi_{1}\right\rangle & =\left| \phi^{+}\right\rangle \\
\left| \phi_{2}\right\rangle & =\left| \phi^{-}\right\rangle \\
\left| \phi_{3}\right\rangle & =\left| \psi^{+}\right\rangle \\
\left| \phi_{4}\right\rangle & =\left| \psi^{-}\right\rangle
\end{align*}
and $\left| \alpha_{i}\right\rangle $ is Bob's normalised and corrected
outcome $\left| \alpha_{i}\right\rangle $ given the measurement result $i$.
The probability of Alice measuring $\left| \phi^{+}\right\rangle $ or
$\left| \phi^{-}\right\rangle $, given the input state $\left|
\psi\right\rangle =\cos\frac{\theta}{2}\left| 0\right\rangle +\sin
\frac{\theta}{2}\exp(i\phi)\left| 1\right\rangle $ is
\[
p(1|\psi)=p(2|\psi)=\frac{1}{2}(\alpha^{2}\cos^{2}\frac{\theta}{2}+\beta
^{2}\sin^{2}\frac{\theta}{2})
\]
and of measuring $\left| \psi^{+}\right\rangle $ or $\left| \psi
^{-}\right\rangle $ is
\[
p(3|\psi)=p(4|\psi)=\frac{1}{2}(\alpha^{2}\sin^{2}\frac{\theta}{2}+\beta
^{2}\cos^{2}\frac{\theta}{2})
\]
The fidelity is then
\[
F(\left| \psi\right\rangle )=\cos^{4}\frac{\theta}{2}+\sin^{4}\frac{\theta
}{2}+\alpha\beta\sin^{2}\theta
\]
Averaged over all initial states, this gives
\begin{align}
F_{av} & =\frac{1}{4\pi}\int_{0}^{2\pi}\int_{0}^{\pi}(\cos^{4}\frac{\theta
}{2}+\sin^{4}\frac{\theta}{2}+\alpha\beta\sin^{2}\theta)\sin\theta d\theta
d\phi\label{eq:diruni}\\
& =\frac{2}{3}(1+\alpha\beta)\nonumber
\end{align}
It can be shown, using a result of the Horodeckis, \cite{Horodecki98}, that
the average fidelity given in Eq. (\ref{eq:diruni}) is optimal for any
teleportation scheme, whatever Alice's measurement or Bob's corrections. The
Horodeckis derive a general relation between the optimal fidelity of
teleportation $\ F_{tele}$ and the maximal singlet fraction $f$, defined
below, of the state used for teleportation
\[
F_{tele}=\frac{2f+1}{3}
\]
For the non-maximally entangled state $\alpha\left| 00\right\rangle
+\beta\left| 11\right\rangle $, the maximal singlet fraction is
\begin{align*}
f & =|\frac{1}{\sqrt{2}}(\langle00|+\langle11|)(\alpha\left|
00\right\rangle +\beta\left| 11\right\rangle )|^{2}\\
& =\frac{1}{2}(1+2\alpha\beta)
\end{align*}
and hence the optimal fidelity of teleportation is given by Eq.
(\ref{eq:diruni}).
In the two-state case, where Alice has either $\left| \psi_{1}\right\rangle $
$=\cos(\frac{\theta}{2})\left| 0\right\rangle +\sin(\frac{\theta}{2})\left|
1\right\rangle $ or $\left| \psi_{2}\right\rangle $ $=\sin(\frac{\theta}
{2})\left| 0\right\rangle +\cos(\frac{\theta}{2})\left| 1\right\rangle $
with equal probabilities, the fidelity is
\begin{equation}
F=\cos^{4}\frac{\theta}{2}+\sin^{4}\frac{\theta}{2}+\alpha\beta\sin^{2}
\theta\label{eq:dirtwo}
\end{equation}
When $\left| \psi_{1}\right\rangle $ and $\left| \psi_{2}\right\rangle $ are
not orthogonal, the fidelity can only be unity if the channel is maximally
entangled, $\alpha=\beta=\frac{1}{\sqrt{2}}$.
Another strategy for teleportation is based on first purifying the channel.
Purification has some probability to convert the state to a maximally
entangled state, which can achieve perfect teleportation, and some probability
to fail so that no entanglement is shared, and Alice and Bob must revert to
the classical methods for sending the state with no shared entanglement. For a
single copy, the best purification is the `Procrustean' method,
\cite{Bennett96}, which has optimal efficiency $2\alpha^{2}$, \cite{Lo97}.
When the purification fails, Alice and Bob are left with a product state. The
input state is unaffected by purification, so Alice may employ the best
strategy for transmitting the state without entanglement. For a completely
unknown input state, the fidelity is $F_{cl}=\frac{2}{3}$, hence the fidelity is
\begin{equation}
F=\frac{2}{3}(1+\alpha^{2}) \label{eq:purif}
\end{equation}
Higher fidelities are achieved in the two-state case. Then the best fidelity
which may be achieved is
\begin{equation}
F=2\alpha^{2}+(1-2\alpha^{2})F_{cl} \label{eq:puriftwo}
\end{equation}
where
\[
F_{cl}=\cos^{2}\frac{\theta}{2}\cos^{2}(\frac{\theta-\alpha}{2})+\sin^{2}
\frac{\theta}{2}\sin^{2}(\frac{\theta+\alpha}{2})
\]
is the best measurement strategy with no entanglement with
\[
\alpha=\tan^{-1}\left( \frac{\sin\theta}{\cos^{2}\theta}\right)
\]
For a completely unknown input state, teleporting directly through the
non-maximally entangled channel is always better than the strategy based on
purification, Eq. (\ref{eq:purif}), since $\alpha\leq\beta$, see Fig.
(\ref{fig:uni}).
\begin{figure}
\caption{Teleportation through a non-maximally entangled channel for unknown
state. The dotted line shows the purification method, Eq. (\ref{eq:purif}
\label{fig:uni}
\end{figure}
For two input states, on the other hand, the fidelities of the different
methods are plotted in Fig. (\ref{fig:comb}). The direct method is no longer
always better than the purification method, though it is better when the
entanglement in the channel is high, in which case it approaches the average
fidelity. For low entanglement, the efficiency of the direct method falls off
steeply and becomes worse even than the classical strategy without entanglement.
For a completely unknown state, teleportation via either strategy is always
better than the classical method of measuring and communicating the result.
However, when there are only two possible input states, a large amount of
information may be gained just by Alice measuring the state she has. It turns
out that the fidelity which may be achieved by Alice measuring her state and
telling Bob the result classically is higher than a direct teleportation, if
the channel has low entanglement. On the other hand, when the channel is first
purified, it is possible to take advantage of the high classical fidelity, by
employing the classical strategy when the purification fails. It is possible
to do this because it is known when the purification has failed. Hence in the
two-state case, the purification method is better for low entanglement than
the direct method.
In the two-state case, it is not known what is the optimal teleportation
scheme is. The best bound we have found is based on a combination of the
direct and purification methods. This may be achieved by Alice partially
purifying the entangled channel, $\alpha\left| 00\right\rangle +\beta\left|
11\right\rangle $ to a more entangled channel, $\alpha^{\prime}\left|
00\right\rangle +\beta^{\prime}\left| 11\right\rangle $, where $\alpha
^{\prime}\geq\alpha$. The probability of succeeding in this purification is
$P_{s}=\left( \frac{\alpha}{\alpha^{\prime}}\right) ^{2}$. If the
purification succeeds, the direct method may be employed on the more entangled
state. If it fails, the best classical strategy must be employed. Hence the
fidelity is given by
\begin{equation}
F=\left( \frac{\alpha}{\alpha^{\prime}}\right) ^{2}F_{dir}(\alpha^{\prime
})+(1-\left( \frac{\alpha}{\alpha^{\prime}}\right) ^{2})F_{class}
\label{eq:comb}
\end{equation}
For a particular non-maximally entangled channel, $\alpha$, this fidelity is
maximised by purifying to a particular channel characterised by $\alpha
^{\prime}$.
\begin{figure}
\caption{Teleportation through a non-maximally entangled channel for two
states with $\theta=\frac{\pi}
\label{fig:comb}
\end{figure}
\section{Relation to telecloning\label{sec:cloning}}
Limitations on the fidelity of teleportation can be related to limitations on
the fidelity of cloning non-orthogonal quantum states. When a perfect
teleportation is achieved, there should be no information about the state left
on Alice's side which would enable her to construct any approximate copy of
the state in addition to the perfectly teleported state. Teleportation using a
maximally entangled pair achieves perfect fidelity, and the measurement on
Alice's side provides no information since the probability of obtaining the
different measurement outcomes is independent of the input state. This was
also indicated by Nielsen and Caves, \cite{Nielsen97}, who showed that
teleportation is a special case of reversing a quantum measurement, and that a
necessary condition for reversibility of a general quantum operation is that
no information about the prior state be obtainable from the measurement. On
the other hand, if the channel is not maximally entangled, perfect
teleportation cannot be achieved and Alice's measurement may provide some
information about the input state. We have seen that when there is no
entanglement in the channel at all, the optimal strategy is for Alice to
extract as much information as possible from her measurement. The measurement
result may then be used to prepare an arbitrary number, $M$, of identical
imperfect copies of the original state with fidelity given by Eq.
(\ref{eq:fid}). This type of cloning has been called `classical cloning',
\cite{Gisin97}, to distinguish it from the more general operation of quantum
cloning which is based on unitary evolution of the input with an ancilla.
Quantum cloning can achieve higher fidelities than classical cloning for a
finite number of copies $M$. The process of quantum cloning allows the use of
more entanglement than classical cloning since the ancilla may remain
entangled to the input and the copies, which may also be entangled to one
another. For two-state teleportation through a non-maximally entangled
channel, there is a trade-off between the classical cloning based on directly
measuring the input state, and the fidelity that can be achieved by
teleportation based on the entanglement. The exact relation between the
constraints on sharing information amongst copies in cloning and in
teleportation is a topic for further research. However, one way in which the
relationship between cloning and teleportation may be pursued is through a
combination of the two procedures in `telecloning'. We now investigate the
effect of a priori information on this protocol.
\subsection{State-dependent telecloning\label{sec:teleclone}}
Teleportation has been combined with optimal universal cloning from one to $M$
\ copies, \cite{Murao99}. This is achieved by performing the usual
teleportation protocol but with the entangled channel being a multiparticle
entangled state, called the `telecloning' state. For $M=2$, the telecloning
state is a $4$-qubit state
\[
\left| \psi_{TC}\right\rangle =\frac{1}{\sqrt{2}}(\left| 0\right\rangle
\left| \phi_{0}\right\rangle +\left| 1\right\rangle \left| \phi
_{1}\right\rangle )\label{eq:tcstate}
\]
where $\left| \phi_{0}\right\rangle $ and $\left| \phi_{1}\right\rangle $
are the optimal cloning states produced by acting with the optimal cloning
transformation $U_{12}$ on $\left| 0\right\rangle $ and $\left|
1\right\rangle $ respectively,
\begin{align*}
\left| \phi_{0}\right\rangle & =U_{12}(\left| 0\right\rangle _{A}\left|
00\right\rangle )=\sqrt{\frac{2}{3}}\left| 0\right\rangle _{A}\left|
00\right\rangle +\sqrt{\frac{1}{6}}\left| 1\right\rangle _{A}(\left|
01\right\rangle +\left| 10\right\rangle )\\
\left| \phi_{1}\right\rangle & =U_{12}(\left| 0\right\rangle _{A}\left|
10\right\rangle )=\sqrt{\frac{2}{3}}\left| 1\right\rangle _{A}\left|
11\right\rangle +\sqrt{\frac{1}{6}}\left| 0\right\rangle _{A}(\left|
01\right\rangle +\left| 10\right\rangle )
\end{align*}
where subscript $A$ denotes the ancilla. In the telecloning state, the first
two qubits and the `port' are held by Alice and the last two qubits belong to
two distant users, Bob and Claire. When the other qubits are traced over after
telecloning, these yield the optimal clones of Alice's input state. The total
amount of entanglement between Alice and the other users, given by the Von
Neumann entropy of the reduced density matrix after tracing over one side, was
found to be $\log(3)$, clearly less than the two units of entanglement
required if cloning is performed first and then the standard teleportation.
Adapting the telecloning scheme to communicating two states produces a
surprising result in terms of the amount of entanglement required. Bruss
\textit{et al.}, \cite{Bruss98}, have found the optimal cloning transformation
$U$ with respect to the global fidelity for two-state cloning from one copy to
two. An ancilla is not necessary. Following the same procedure as in the
universal case for constructing the telecloning state, we may add an ancilla,
giving the cloned states to be
\begin{align*}
\left| \phi_{0}\right\rangle & =U_{12}(\left| 0\right\rangle _{A}\left|
00\right\rangle )=a\left| 0\right\rangle _{A}\left| 00\right\rangle
+b\left| 1\right\rangle _{A}(\left| 01\right\rangle +\left| 10\right\rangle
)+c\left| 0\right\rangle _{A}\left| 11\right\rangle )\\
\left| \phi_{1}\right\rangle & =U_{12}(\left| 0\right\rangle _{A}\left|
10\right\rangle )=c\left| 1\right\rangle _{A}\left| 00\right\rangle
+b\left| 0\right\rangle _{A}(\left| 01\right\rangle +\left| 10\right\rangle
)+a\left| 1\right\rangle _{A}\left| 11\right\rangle )
\end{align*}
where $a$, $b$ and $c$ depend on the overlap of the two states, as given in
the paper \cite{Bruss98}. The telecloning state is constructed just as before,
Eq. (\ref{eq:tcstate}). The ancilla is required in order that the recipients
may use the standard Pauli rotations to correct their state after they receive
the classical message from Alice. Notice however that $\left| \phi
_{0}\right\rangle $ and $\left| \phi_{1}\right\rangle $ are no longer the
optimal clones. The fidelity of cloning is shown in Figure (\ref{fig:newfil}).
\begin{figure}
\caption{The global fidelity of the clones produced in the telecloning scheme,
(solid line), as compared to the optimal global fidelity for two-state
cloning, (dotted line).}
\label{fig:newfil}
\end{figure}
The reduced density matrix found by tracing the density matrix for the
telecloning state over Alice's two qubits is
\[
\rho_{34}=\frac{1}{2}\left(
\begin{array}
[c]{cccc}
a^{2}+b^{2}+c^{2} & 0 & 0 & 2a(b+c)\\
0 & b^{2} & 0 & 0\\
0 & 0 & b^{2} & 0\\
2a(b+c) & 0 & 0 & a^{2}+b^{2}+c^{2}
\end{array}
\right)
\]
\begin{figure}
\caption{Entanglement between Alice and receivers in telecloning}
\label{fig:tclone}
\end{figure}
The entanglement between the two sides now increases with the overlap of the
two states $\left| \psi_{1}\right\rangle $ and $\left| \psi_{2}\right\rangle
$, but is always less than $\log(3)\approx1.585$, see Fig. (\ref{fig:tclone}).
However each qubit is maximally mixed so the entanglement between any one
qubit and the other three is one. This means that Alice's port qubit does
share a unit of entanglement with the other three qubits. This is consistent
with the requirement that perfect teleportation of two states employ a full
unit of entanglement. In this telecloning scheme, the amount of overall
entanglement is lower than in the universal case. It is an interesting
question whether a telecloning scheme giving the optimal two-state cloning
fidelity would also require less entanglement.
\section{Conclusion}
In this paper, we have shown the surprising result that a priori knowledge
makes no difference to the amount of entanglement required for perfect
teleportation. We have computed lower bounds for two-state teleportation
fidelity using a non-maximally entangled pure state as a channel, and the
exact result for the two-state fidelity with no entanglement.
This work opens a number of possible directions for future research. In this
paper, only pure entangled states were considered as channels for
teleportation. The investigation could be extended to mixed entangled states
also. The relationship between cloning and teleportation with a priori
knowledge could be investigated further by finding the amount of entanglement
required by a state-dependent telecloning scheme which preserves the
optimality of the clones produced. Asymmetric telecloning or general $N$ to
$M$ state-dependent telecloning could also be considered. It may be possible
to quantify exactly the relationship between the amount of information Alice
gains from her measurement, the amount of entanglement in the channel and
Bob's information. Our work provides a different way of understanding the
respective roles of classical information and quantum entanglement in the new
field of quantum information processing.
\textbf{Acknowledgments}
We thank Dagmar Bruss, Artur Ekert, Chiara Macchiavello, Mio Murao and Martin
Plenio for helpful discussions. L. Henderson acknowledges financial support of
the Rhodes Trust. L. Hardy thanks the Royal Society for funding.
\end{document} | math |
कोविड-१९: दिल्ली में बढ़ता जा रहा कोरोना का कहर, २३ और मिले पॉजिटिव
३१ मार्च को उत्तराखंड में आवाजाही की नहीं मिलेगी छूट, सरकार ने वापस लिया फैसला
कोरोना वायरस के चलते म्यूचुअल फंड में निवेशकों को नुकसान, एक महीन में २५ फीसदी कम रिटर्न
बाजार में बिकवाली से म्यूचुअल फंड रिटर्न में अब २५ फीसदी तक की गिरावट आई है.
आईफास्ट फाइनेशियल इंडिया में वरिष्ठ शोध विश्लेषक कृष्णा करवा ने कहा कि कोविड-१९ महामारी के आर्थिक असर से देश की प्रमुख ४४ म्यूचुअल फंड कंपनियां भी बच नहीं सकी हैं.
नई दिल्ली. इक्विटी आधारित म्यूचुअल फंड (इक्विटी मुच्युअल फंड) योजनाओं में निवेश करने वाले निवेशकों का रिटर्न पिछले एक महीने में २५ प्रतिशत गिरा है. कोरोना वायरस महामारी के चलते मंदी की आशंका से बाजार में भारी गिरावट देखने को मिली है.
यह भी पढ़ें: कोरोना के डर से कहीं आपने तो बंद नहीं की म्युचूअल फंड्स सीप, जानें अब क्या
छोटी और मिडकैप इक्विटी पर सबसे अधिक दबाव
बाजार में अस्थिरता के कारण छोटी से मध्यम अवधि के दौरान छोटी और मिड-कैप इक्विटी योजनाएं दबाव में रहेंगी. मॉर्निंग स्टार इंडिया के आंकड़ों के अनुसार इक्विटी योजना श्रेणी में सभी इक्विटी आधारित बचत योजनाओं (ईएलएसएस), स्मॉल कैप, मिडकैप और लार्ज-कैप योजनाओं ने १९ फरवरी से १८ मार्च २०२० के बीच २५-२६ प्रतिशत के बीच नकारात्मक प्रतिफल दिया है.
बाजार में भारी गिरावट का दौर
इसी अवधि के दौरान बीएसई सेंसेक्स लगभग ३० प्रतिशत गिर गया. कोरोना वायरस महामारी और अन्य कारणों के चलते सूचकांक ४१,००० के स्तर से गिरकर २९,००० के स्तर तक नीचे आ गया. मॉर्निंग स्टार के शोध निदेशक कौस्तुभ बेलापुरकर ने कहा, हमने बाजार में इस तरह की गिरावट कई बार देखी है. निराशावाद कुछ समय तक बना रह सकता है, क्योंकि कोरोना वायरस के प्रसार को लेकर अनिश्चित स्थिति है. लेकिन जैसा कि हमने पहले भी देखा है, लंबी अवधि में बाजार ठीक हो जाएगा.
यह भी पढ़ें: इस राज्य में पेट्रोल-डीजल हो गए महंगे, सरकार ने बढ़ाया ४% वैट | hindi |
using System;
using Android.Runtime;
using Android.Animation;
using Stencil.Native.Core;
namespace Stencil.Native.Droid.Core.UI
{
public class DroidHexColorEvaluator : ArgbEvaluator
{
public DroidHexColorEvaluator()
:base()
{
}
public DroidHexColorEvaluator(IntPtr handle, JniHandleOwnership transfer)
:base(handle, transfer)
{
}
public override Java.Lang.Object Evaluate(float fraction, Java.Lang.Object startValue, Java.Lang.Object endValue)
{
return CoreUtility.ExecuteFunction<Java.Lang.Object>("Evaluate", delegate()
{
Java.Lang.Object result;
int startInt = Convert.ToInt32(startValue);
int startA = (startInt >> 24) & 0xff;
int startR = (startInt >> 16) & 0xff;
int startG = (startInt >> 8) & 0xff;
int startB = startInt & 0xff;
int endInt = Convert.ToInt32(endValue);
int endA = (endInt >> 24) & 0xff;
int endR = (endInt >> 16) & 0xff;
int endG = (endInt >> 8) & 0xff;
int endB = endInt & 0xff;
result = ((startA + (int)(fraction * (endA - startA))) << 24) |
((startR + (int)(fraction * (endR - startR))) << 16) |
((startG + (int)(fraction * (endG - startG))) << 8) |
((startB + (int)(fraction * (endB - startB))));
return result;
});
}
}
}
| code |
बिजली कन्वेयर पिज्जा ओवन ल्ड-२स
स्टेनलेस स्टील बिजली पिज्जा ओवन (एब-२)
न्यूनतम आदेश मात्रा:१ यूनिट/यूनिट ओएम सेवा स्वीकार किए जाते हैं
स्टेनलेस स्टील हलोजन ओवन एब-४आ
एफओबी मूल्य:उस $ ८८-१००० /डिब्बों
आर्थिक बिजली ओवन (एब-८ब)
बिजली स्टेनलेस स्टील पिज्जा ओवन (एब-१)
न्यूनतम आदेश मात्रा:२ यूनिट/यूनिट ओएम सेवा स्वीकार किए जाते हैं
बिजली मक्का भुनने एब-१८-२
वाणिज्यिक ४ परतों परिप्रेक्ष्य बिजली संवहन ओवन एब-४आ
न्यूनतम आदेश मात्रा:१५ यूनिट/यूनिट ओएम सेवा स्वीकार किए जाते हैं
बिजली पिज्जा ओवन/वाणिज्यिक पिज्जा ओवन के लिए/पिज्जा ओवन एब-२
स्टेनलेस स्टील परिप्रेक्ष्य संवहन ओवन बिजली ४ परतों
बिजली कन्वेयर पिज्जा ओवन ल्ड-१स (००८६-१3580546328)
डबल परत बिजली पिज्जा ओवन (एब-२)
रेस्तरां पिज्जा ओवन
स्टेनलेस स्टील एलपीजी गैस ओवन गब-३२८
कन्वेयर पिज्जा ओवन ल्ड-१स | hindi |
{\rm tr}gin{document}
\thispagestyle{empty}
{\rm tr}gin{center} \LARGE
{\bf On the integration of \\ Poisson homogeneous spaces}
\\[12mm] \normalsize
{\mbox{$\mathfrak g$}rge\bf Francesco Bonechi$^{a}$, Nicola Ciccoli $^{b}$, Nicola Staffolani $^{c}$ and Marco Tarlini$^{a}$} \\[8mm]
{\small{\rm i}t
$^a$I.N.F.N. Sezione di Firenze,\\
Via G. Sansone 1, 50019 Sesto Fiorentino - Firenze, Italy \\
email: $\mbox{$\mathfrak g$}ngle name \rangle$ @fi.infn.it
~\\
$^b$Dipartimento di Matematica e Informatica,\\
Via Vanvitelli 1, 06123 - Perugia, Italy\\
email: ciccoli@dipmat.unipg.it
~\\
$^c$Dipartimento di Fisica,\\
Via G. Sansone 1, 50019 Sesto Fiorentino - Firenze, Italy \\
email: staffolani@fi.infn.it
}
{\rm e}nd{center}
\centerline{\bfseries Abstract} We study a reduction procedure for describing the symplectic groupoid of a
Poisson homogeneous space obtained by quotient of a coisotropic subgroup. We perform it as a reduction of the Lu-Weinstein symplectic groupoid integrating Poisson Lie groups, that is suitable even for the non-complete case.
\noindent {\bf Keywords:} Poisson geometry, Symplectic groupoids, Poisson homogeneous spaces,
Poisson-Lie groups, Coisotropic subgroups, Geometric quantization.
\noindent {\bf MSC:} 53D05, 17B63, 22A22, 53D17, 53D50
\noindent {\bf JGP subject code:} Symplectic geometry
{\rm e}ject
\normalsize
\section{Introduction}
Symplectic groupoids were introduced by Karasev and Weinstein in the 80's, \cite{Ka,We1987} as a tool to quantize Poisson
manifolds. They immediately became objects of independent math interests and one of the cornerstones of Poisson geometry. Our
knowledge on their role dramatically improved after the work by Cattaneo-Felder \cite{CaFe}, interpreting them as the phase space
of the Poisson sigma model, and Crainic-Fernandes \cite{CrFe} on the integrability of algebroids. On the contrary, quantum
aspects were much less studied: in \cite{XW} P.Xu and A.Weinstein defined the right notion of prequantization. Such a prequantization
can be explicitly constructed by reducing the prequantization of the phase space of the Poisson sigma model, as shown in \cite{BCZ}. In \cite{We2} the so-called noncommutative torus was recovered by the geometric quantization of the symplectic groupoid integrating the underling symplectic structure. Very recently, a notion of polarization of symplectic groupoids has been introduced in \cite{H}. Very roughly, the idea is to associate to any Poisson manifold a $C^*$-algebra constructed out of the space of polarized sections. This idea realizes a fundamental pattern in noncommutative geometry, where according to the Gelfand-Naimark theorem the noncommutative counterpart of the algebra of continuous functions on a (compact) manifold is a $C^*$-algebra.
During the same years, following the impulse of A. Connes, noncommutative geometry evolved trying to give an axiomatic description of what a noncommutative manifold should be. The most studied examples can be collected in two main classes: $i$) the so-called $\theta$-manifolds, where the underlying Poisson structure is determined by the action of an abelian group, like the celebrated noncommutative torus, and the Connes-Landi $4$-sphere, see \cite{CL} and also {\cite{CDV}}; $ii$) quantum groups and the associated homogeneous spaces. The $\theta$-manifolds are well studied from many different points of view: the symplectic groupoid was described first in \cite{Xu1}, their deformation quantization in \cite{Rieffel} and the polarization of the symplectic groupoid in \cite{H}. On the contrary, for spaces related to quantum groups less is known. The Poisson Lie groups, that are the semiclassical limit of quantum groups, were shown to be integrable in \cite{LW}. The problem of Poisson reduction of the symplectic groupoid was discussed in \cite{Xu}: from these results the integration of Poisson homogeneous spaces that are quotient by Poisson Lie subgroups can be obtained. With a completely different approach, Poisson symmetric spaces (a definition which does not contain all covariant Poisson structures on symmetric spaces) were shown to be integrable in \cite{Xu2}. Nothing is known concerning the quantization of the symplectic groupoid.
Much information about quantum aspects comes from quantum group theory, especially for what concerns the study of $C^*$-algebras of basic examples of quantum groups and homogeneous spaces. It is an interesting program to look at these constructions from the point of view of the quantization of the symplectic groupoid like the one proposed in \cite{H}.
When we started this project, we realized that there was no construction of symplectic groupoids integrating the most important examples of Poisson homogeneous spaces coming from the semiclassical limit of homogeneous spaces of quantum groups, like Podles spheres, odd spheres, quantum grassmanians. The most relevant properties of the underlying Poisson structures is that they can be obtained as quotients by coisotropic subgroups. The present paper is devoted to this construction and must be thought of as preliminary to the problem of quantization, that we hope to address in the future.
While we were finishing this paper, we were aware of \cite{Lu2007}, where a Poisson groupoid on any Poisson homogeneous space is presented. Moreover, conditions for the Poisson structure to be nondegenerate, so giving a symplectic groupoid, are discussed. The paper \cite{Lu2007} covers a large part of our results, that we obtained independently; in particular in the complete case it gives the symplectic groupoid that we describe in Theorem \ref{thm_groupoid}. Nevertheless, since the two approaches are different we think that our paper can help to clarify some issues. The differences between our paper and \cite{Lu2007} come out in the discussion of the noncomplete case ({{\rm i}t i.e.} when dressing vector fields are not complete). In fact under a weaker hypothesis about the integrability of dressing vector fields (that we call {{\rm i}t relative completeness}), we always obtain a symplectic groupoid. In concrete examples we show that the constructions are different.
This is the plan of the paper. In section 2 we recall very basic facts about Poisson manifolds and symplectic groupoids, mainly to fix notations. In section 3 we recall basic facts of Poisson Lie groups, following \cite{LuTh}. In section 4 we discuss the reduction procedure in terms of a moment map. When the Poisson Lie group is complete, the reduction is a straightforward analogue of the trivial case, where the action given by left multiplication of the subgroup can be lifted to a hamiltonian action on $T^*G$ and the groupoid is obtained by Marsden-Weinstein reduction. Indeed if the Poisson Lie group $G$ is complete then the left multiplication can be lifted to the groupoid and this action is hamiltonian in terms of Lu's momentum map. In the noncomplete case, the action can be lifted only as an infinitesimal action, and it is better to formulate it in terms of the symplectic action of the groupoid integrating the dual Poisson Lie group $G^*$. Nevertheless, if the subgroup satisfies the condition of relative completeness the procedure still works.
\section{Preliminaries on Poisson manifolds}
In this section we introduce the main definitions concerning the theory of Poisson manifolds and symplectic groupoids.
A {{\rm i}t Poisson manifold} $P$ is a smooth manifold provided with a bivector ${\rm p}i_P{\rm i}n {\cal G}amma(\Lambdambda^2TP)$ satisfying $[{\rm p}i_P,{\rm p}i_P]_S=0$, where $[,]_S$ is the Schouten bracket between multivector fields. The cartesian product $P=M\times N$ of two Poisson manifolds is a Poisson manifold with Poisson tensor ${\rm p}i_{M\times N}={\rm p}i_M+{\rm p}i_N$. The Poisson bivector ${\rm p}i_P$ defines a bundle map ${\rm p}i_P^\sharp:T^*P\rightarrow TP$ as $\mbox{$\mathfrak g$}ngle {\rm p}i^\sharp_P(\mbox{$\omega$}ega_p),\nu_p\rangle = \mbox{$\mathfrak g$}ngle {\rm p}i_P(p),\nu_p\wedge \mbox{$\omega$}ega_p\rangle$, for $p{\rm i}n P$, $\mbox{$\omega$}ega_p,\nu_p{\rm i}n T^*_pP$.
A submanifold $C$ of $P$ is a {{\rm i}t coisotropic submanifold} if
${\rm p}i^\sharp_P \left( N^* C \right) \subset TC$, where $N^* C$ is the conormal bundle of $C$, $N^*_x C = \{ \mbox{$\omega$}ega {\rm i}n T^*_x P:~ \mbox{$\mathfrak g$}ngle\mbox{$\omega$}ega , V\rangle = 0,\, \forall\ V {\rm i}n T_x C\}$, for all $x {\rm i}n C$. The generalized distribution defined by ${\rm p}i_P^\sharp(N^*C)$ is integrable and the space $\underline{C}$ of coisotropic leaves, if smooth, is a Poisson manifold. A submanifold $C$ is a {{\rm i}t Poisson submanifold} if ${\rm p}i_P(c){\rm i}n\Lambdambda^2T_cC$; it is coisotropic and the coisotropic foliation is trivial. A smooth map $\Psi:M\rightarrow N$ between two Poisson manifolds is a {{\rm i}t Poisson map} if the Poisson tensors are $\Psi$-related. In \cite{We1} it is proven that if $\Psi: M \rightarrow N$ is a Poisson map and $\mathcal{O}_N \subset N$ is a symplectic leaf then $\Psi^{-1} (\mathcal{O}_N) \subset M$, whenever is a submanifold, is coisotropic.
Let ${\cal G}=({\cal G},{\cal G}_0,\mathit{a}lpha_{\cal G},{\rm tr}ta_{\cal G},m_{\cal G},{\rm i}ota_{\cal G},{\rm e}psilon_{\cal G})$ be a Lie groupoid over the space of unities ${\cal G}_0$, where $\mathit{a}lpha_{\cal G}, {\rm tr}ta_{\cal G}:{\cal G}\rightarrow {\cal G}_0$ are the source and target maps, respectively, $m_{\cal G}:{\cal G}^{(2)}\rightarrow{\cal G}$ is the multiplication, ${\rm i}ota_{\cal G}:{\cal G}\rightarrow{\cal G}^{-1}$ is the inversion and ${\rm e}psilon_{\cal G}:{\cal G}_0\rightarrow{\cal G}$ is the embedding of unities. Our conventions are that $(x_1,x_2){\rm i}n{\cal G}^{(2)}$ if ${\rm tr}ta_{\cal G}(x_1)=\mathit{a}lpha_{\cal G}(x_2)$. We say that ${\cal G}$ is source simply connected (ssc) if $\mathit{a}lpha_{\cal G}^{-1}(m)$ is connected and simply connected for any $m{\rm i}n {\cal G}_0$.
A {{\rm i}t symplectic groupoid} is a Lie groupoid, which is equipped with a symplectic form, such that the graph
of the multiplication is a lagrangian submanifold of ${\cal G} \times {\cal G} \times \bar{\cal G}$, where $\bar{\cal G}$ means $\cal G$ with the opposite symplectic structure.
There exists a unique Poisson structure on ${\cal G}_0$ such that $\mathit{a}lpha_{\cal G}$ and ${\rm tr}ta_{\cal G}$ are Poisson and anti-Poisson mappings, respectively. A Poisson manifold is said to be integrable if it is the space of units of a symplectic groupoid.
An equivalent characterization for a Lie groupoid $\cal G$ to be a symplectic groupoid is that the symplectic form $\mbox{$\omega$}ega$ of $\cal G$ be multiplicative, {{\rm i}t i.e.} let ${\rm p}rGuno$, ${\rm p}rGdue: {\cal G}^{(2)}\rightarrow {\cal G}$ be respectively the projections onto the first and
second factor, then $m^*_{\cal G} \mbox{$\omega$}ega = {\rm p}rGuno^* \mbox{$\omega$}ega + {\rm p}rGdue^* \mbox{$\omega$}ega$.
Following \cite{MW}, we define the left action of $\cal G$ on a manifold $P$ with anchor $J:P\rightarrow {\cal G}_0$ a mapping from ${\cal G}{}_{{\rm tr}ta_{\cal G}}\times_J P=\{(x,p){\rm i}n{\cal G}\times P\,|\,{\rm tr}ta_{\cal G}(x)=J(p)\}$ to $P$, given by $(x,p)\rightarrow xp$ such that
{{\rm i}t i}) $J(xp)=\mathit{a}lpha_{\cal G}(x)$, {{\rm i}t ii}) $(xy)p =x(yp)$, {{\rm i}t iii}) ${\rm e}psilon(J(p))p=p$. In the case of $P$ symplectic, the action of ${\cal G}$ is called {{\rm i}t symplectic} if the graph of the action $\{(x,p,xp), {\rm tr}ta_{\cal G}(x)=J(p)\}$ is lagrangian in ${\cal G}\times P\times \bar P$. In \cite{MW} it is shown that $J:P\rightarrow {\cal G}_0$ is a Poisson map. Symplectic reduction is defined as follows. The isotropy group ${\cal G}^m_m=\mathit{a}lpha^{-1}_{\cal G}(m)\cap{\rm tr}ta^{-1}_{\cal G}(m)$ of $m{\rm i}n {\cal G}_0$ leaves invariant $J^{-1}(m)$ and ${\cal G}^m_m\backslash J^{-1}(m)$, whenever a manifold, is symplectic.
\section{The symplectic groupoid of a Poisson Lie group}
In this section we recall basic results of the theory of Poisson Lie groups, and of the symplectic groupoid integrating them. The presentation follows \cite{LuTh}.
A {{\rm i}t Poisson Lie group} $G$ is a Poisson manifold and a Lie group whose multiplication map $G \times G \rightarrow G$ is a Poisson map, where $G \times G$ is endowed with the product Poisson structure.
In terms of the Poisson bivector field ${\rm p}i_G$, it means that
{\rm tr}gin{equation}\mbox{$\mathfrak g$}bel{multiplicativity}
{\rm p}i_G (gh) = l_g {\rm p}i_G (h) + r_h {\rm p}i_G (g), \, \forall g,h {\rm i}n G\, ,
{\rm e}nd{equation}
where $l_g$ ($r_g$) stands for the left (right) group multiplication by $g$, as well as for the induced tangent map. A multivector field satisfying (\ref{multiplicativity}) is said to be {{\rm i}t multiplicative}.
A left action $\sigma : G \times P \rightarrow P$ of a Poisson Lie Group $G$ on a Poisson manifold $P$ is called a {{\rm i}t Poisson action} if $\sigma$ is a Poisson map, where $G \times P$ is endowed with the product Poisson structure. In terms of the Poisson bivectors ${\rm p}i_G$ of $G$ and ${\rm p}i_P$ of $P$, $\sigma$ is a Poisson action if, for any $g{\rm i}n G$ and $p{\rm i}n P$, we have that
$$
{\rm p}i_P(\sigma(g,p))=g_*{\rm p}i_P(p) + p_*{\rm p}i_G(g)\;,
$$
where $g:P\rightarrow P$, $g(p)=\sigma(g,p)$ and $p:G\rightarrow P$, $p(g)=\sigma(g,p)$.
A {{\rm i}t Lie bialgebra} is the couple $(\mathfrak{g},\mathfrak{g}^\star)$, where $\mathfrak{g}={\rm Lie} G$ and its dual $\mathfrak{g}^\star$ is a Lie algebra with bracket map $[~,~]_{\mathfrak{g}^\star}$ such that ${\rm d}elta=[,]_{\mathfrak{g}^\star}^*:\mathfrak{g}\rightarrow\Lambdambda^2\mathfrak{g}$ is a $1$-cocycle on $\mathfrak{g}$ relative to the adjoint representation of $\mbox{${\mathfrak g}$}$ on $\wedge^2 \mathfrak{g}$.
Let us assume that the group $G$ is connected and
simply connected.
{\rm tr}gin{thm}\mbox{$\mathfrak g$}bel{bialgebrasversuspoissonlie}
There is a one to one correspondence between connected and simply connected Poisson Lie groups and Lie bialgebras.
{\rm e}nd{thm}
{\rm tr}gin{dfn}
The \textbf{double Lie algebra} $\mathfrak{d} = \mbox{${\mathfrak g}$} \bowtie \mbox{${\mathfrak g}$}^\star$ of the Lie bialgebra $(\mbox{${\mathfrak g}$}, \mbox{${\mathfrak g}$}^\star)$ is defined as the vector space $\mbox{${\mathfrak g}$} \mbox{$\Omega^{1}(P)$}lus \mbox{${\mathfrak g}$}^\star$ endowed with the unique Lie bracket structure such that
{\rm tr}gin{itemize}
{\rm i}tem[${\rm i}math$)] it restricts to the given Lie brackets on $\mbox{${\mathfrak g}$}$ and $\mbox{${\mathfrak g}$}^\star$;
{\rm i}tem [${\rm i}math {\rm i}math$)] the symmetric and non-degenerate scalar product on $\mbox{${\mathfrak g}$} \mbox{$\Omega^{1}(P)$}lus \mbox{${\mathfrak g}$}^\star$ defined by
{\rm tr}gin{equation}
\mbox{$\mathfrak g$}ngle X + \xi , Y + {\rm e}ta\rangle= \xi(Y) + {\rm e}ta(X),\, \forall X,Y {\rm i}n \mbox{${\mathfrak g}$},\, \forall \xi, {\rm e}ta {\rm i}n \mbox{${\mathfrak g}$}^\star \nonumber
{\rm e}nd{equation}
is invariant.
{\rm e}nd{itemize}
{\rm e}nd{dfn}
In particular the bracket is defined for any $X,Y{\rm i}n\mathfrak{g}$ and $\xi,{\rm e}ta{\rm i}n\mathfrak{g}^\star$ as
{\rm tr}gin{equation}
\mbox{$\mathfrak g$}bel{bracket_double}
[X+\xi, Y+{\rm e}ta] = [X,Y] -ad^*_{\rm e}ta(X) +ad^*_\xi(Y) + [\xi,{\rm e}ta] + ad^*_X({\rm e}ta) - ad^*_Y(\xi)\;.
{\rm e}nd{equation}
It can be shown that $\mathfrak{d}=\mathfrak{g}\mbox{$\Omega^{1}(P)$}lus\mathfrak{g}^\star$ equipped with the bracket (\ref{bracket_double}) is a Lie algebra if and only if $(\mathfrak{g},\mathfrak{g}^\star)$ is a Lie bialgebra. As a consequence we have that if $(\mbox{${\mathfrak g}$}, \mbox{${\mathfrak g}$}^\star)$ is a Lie bialgebra, then so is $(\mbox{${\mathfrak g}$}^\star ,\mbox{${\mathfrak g}$})$. In particular the connected and simply connected group $G^*$ integrating $\mathfrak{g}^\star$ is a Poisson-Lie group. We call it the {{\rm i}t dual Poisson Lie group} of ($G,{\rm p}i_G$).
The {{\rm i}t double Lie group} $D$ is defined as the connected and simply-connected Lie group with Lie algebra $\mathfrak{d}$. Let ${\rm p}hi_{1}: G \rightarrow D$ and ${\rm p}hi_{2}:
G^* \rightarrow D$ be the Lie group
homomorphisms obtained by respectively integrating the
inclusion maps ${\mathfrak g} {\mathfrak h}ookrightarrow {\mathfrak d}$ and ${\mathfrak g}^\star {\mathfrak h}ookrightarrow {\mathfrak d}$. In the following we denote ${\rm p}hi_1(g)={\overline g}$ and ${\rm p}hi_2(\gammamma)={\overline g}a$.
The following formulas, proved in \cite{LuTh}, describe the Poisson tensor of $G$ and $G^*$ in terms of the group structure of $D$, making explicit the correspondence described in the integration Theorem \ref{bialgebrasversuspoissonlie}. Indeed, let ${\rm p}g:\mathfrak{d}\rightarrow\mathfrak{g}$, ${\rm p}gs:\mathfrak{d}\rightarrow\mathfrak{g}^\star$ be the natural projections; for any $g{\rm i}n G$, $\gammamma{\rm i}n G^*$, $X_i{\rm i}n\mathfrak{g}$ and $\xi_i{\rm i}n\mathfrak{g}^\star$ we have that
{\rm tr}gin{eqnarray}
\mbox{$\mathfrak g$}bel{poisson_tensors}
\mbox{$\mathfrak g$}ngle r_{g^{-1}}{\rm p}i_G(g),\xi_1\wedge\xi_2\rangle &=& -\mbox{$\mathfrak g$}ngle {\rm p}g{\rm Ad}_{{\overline g}^{-1}}\xi_1,{\rm p}gs{\rm Ad}_{{\overline g}^{-1}}\xi_2\rangle ~~~~ g{\rm i}n G,~\xi_i{\rm i}n\mathfrak{g}^\star\;,\cr
\mbox{$\mathfrak g$}ngle r_{\gammamma^{-1}}{\rm p}i_{G^*}(\gammamma),X_1\wedge X_2\rangle &=&\mbox{$\mathfrak g$}ngle {\rm p}g{\rm Ad}_{{\overline g}a^{-1}}X_1,{\rm p}gs{\rm Ad}_{{\overline g}a^{-1}}X_2\rangle\;~~~ \gammamma{\rm i}n G^*, X_i{\rm i}n\mathfrak{g}\;,
{\rm e}nd{eqnarray}
where ${\rm Ad}$ is the adjoint action of $D$.
For further purposes, let us consider the Poisson tensor ${\rm p}i_{+}$ on $D$ defined as follows:
\[ {\rm p}i_{+} (d) ~ = ~ {\mbox{$({\mathfrak g}, ~ {\mathfrak g}^{*})$}ac{1}{2}} (r_{d} {\rm p}i_{0} ~ + ~ l_{d} {\rm p}i_{0}), ~~~~~~~~~d {\rm i}n D, \]
where ${\rm p}i_{0} {\rm i}n {\mathfrak d} \wedge {\mathfrak d}$ is defined by
${\rm p}i_{0} (\xi_{1} + X_{1}, ~ \xi_{2} + X_{2} ) = \mbox{$\mathfrak g$}ngle X_{1}, ~ \xi_{2}\rangle - \mbox{$\mathfrak g$}ngle X_{2}, ~ \xi_{1}\rangle$,
for $\xi_{1} + X_{1}, \xi_{2} + X_{2} {\rm i}n {\mathfrak d}^{*} \cong {\mathfrak g}^\star \mbox{$\Omega^{1}(P)$}lus {\mathfrak g}$. If $d {\rm i}n D$ can be factorized as $d = {\overline g} {\overline g}a$ for some $g {\rm i}n G$ and $\gamma {\rm i}n G^{*}$, then an explicit formula for ${\rm p}i_{+}$ is given by
{\rm tr}gin{eqnarray}
& & \mbox{$\mathfrak g$}ngle (l_{{\overline g}^{-1}}r_{{\overline g}a^{-1}}) {\rm p}i_{+}
(d), (\xi_{1} + X_{1})\wedge (\xi_{2} + X_{2}) \rangle = \mbox{$\mathfrak g$}bel{symplectic_tensor}\\
& = & \mbox{$\mathfrak g$}ngle X_{1}, \xi_{2}\rangle - \mbox{$\mathfrak g$}ngle X_{2}, \xi_{1}\rangle + \mbox{$\mathfrak g$}ngle l_{g^{-1}} {\rm p}i_G(g),\xi_{1}\wedge\xi_{2}\rangle
+ \mbox{$\mathfrak g$}ngle r_{\gamma^{-1}}{\rm p}i_{G^*} (\gammamma), X_{1}\wedge
X_{2}\rangle = \nonumber \\
& = & \mbox{$\mathfrak g$}ngle X_{1}, ~ \xi_{2} + Ad_{{\overline g}a} {\rm p}gs Ad_{{\overline g}a^{-1}} X_{2} \rangle
~ - ~ \mbox{$\mathfrak g$}ngle\xi_{1}, ~ X_{2} + Ad_{{\overline g}^{-1}} {\rm p}g Ad_{{\overline g}} \xi_{2}\rangle \;.\nonumber
{\rm e}nd{eqnarray}
It can be proved that ${\rm p}i_+(g\gammamma)$ is nondegenerate.
If ${\rm p}hi_{1} \times {\rm p}hi_{2}$ is a global diffeomorphism, then we can identify $D$ with $G\times G^*$ and ${\rm p}i_+$ defines a
symplectic structure on the double. Moreover the global decomposition of $D$ defines a left action of $G$ on $G^*$ and a
right action of $G^*$ on $G$. Let $g{\rm i}n G$ and $\gammamma{\rm i}n G^*$ and let $g\gammamma={}^g\gammamma ~g^\gammamma$, where we identify $g$ with
${\overline g}$ and $\gammamma$ with ${\overline g}a$. It is immediate to verify that $(g,\gammamma)\rightarrow {}^g\gammamma$ is a left action of $G$ on
$G^*$ and $(g,\gammamma)\rightarrow g^\gammamma$ is right action of $G^*$ on $G$. These are known as {{\rm i}t dressing actions}. It can be
easily verified that for any $g,g_i{\rm i}n G$ and $\gammamma,\gammamma_i{\rm i}n G^*$ we have that
{\rm tr}gin{equation}\mbox{$\mathfrak g$}bel{properties_dressing}
(g_1 g_2)^\gamma = g_1^{{}^{g_{2}}\gamma} ~ g_2^\gamma~~;~~~~~~~~~
{}^g (\gamma_1 \gamma_2) = {}^g \gamma_1 ~~ {}^{g^{\gamma_{1}}}
\gamma_2~~.
{\rm e}nd{equation}
Such {\rm e}mph{intertwining} property between the two actions defines
what is called a {{\rm i}t matched pair of Lie groups} \cite{Mj,LW2}; we will come back to this notion in Section \ref{generalcase}.
{\rm tr}gin{lem} \mbox{$\mathfrak g$}bel{lem_fund_vec}
The fundamental vector fields associated to the left dressing action of $G$ on $G^*$ and to the right dressing action of $G^*$ on $G$ are respectively:
{\rm tr}gin{equation}\mbox{$\mathfrak g$}bel{dressing_vector_fields}
{\mathcal S}_{X} (\gamma) = {\rm p}i_{G^*}^\sharp (r_{\gamma^{-1}}^* X)~, ~~~~ \forall \gamma {\rm i}n G^*,~~ X {\rm i}n \mbox{${\mathfrak g}$} {\rm e}quiv \left( \mbox{${\mathfrak g}$}^\star \right)^\star~;
{\rm e}nd{equation}
\[
{\mathcal S}_{\xi} (g) = - {\rm p}i_G^\sharp (l_{g^{-1}}^* \xi) ~, ~~~~ \forall g {\rm i}n G, ~~\xi {\rm i}n \mbox{${\mathfrak g}$}^\star~.
\]
{\rm tr}gin{proof}
A direct computation gives the following expressions for the fundamental vector fields associated with the left dressing action
of $G$ on $G^*$ and with the right dressing action of $G^*$ on $G$:
\[
{\mathcal S}_{X} (\gamma) = l_{\gamma} ~ {\rm p}gs
\left( {\rm Ad}_{{\overline g}a^{-1}} X \right), ~~~~ \forall \gamma {\rm i}n G^*, ~~ X {\rm i}n \mbox{${\mathfrak g}$};
\]
\[
{\mathcal S}_{\xi} (g) = r_g ~ {\rm p}g \left( {\rm Ad}_{\overline g}\xi
\right), ~~~~ \forall g {\rm i}n G, ~~ \xi {\rm i}n \mbox{${\mathfrak g}$}^\star.
\]
We have to prove that the pointwise pairing of these vector fields with generic $1$-forms coincide. Then, given $X,Y{\rm i}n \mbox{${\mathfrak g}$}$,$\gamma {\rm i}n G^*$,
{\rm tr}gin{eqnarray}
\mbox{$\mathfrak g$}ngle{\mathcal S}_{X} (\gamma) , r_{\gamma^{-1}}^* Y\rangle &=&
\mbox{$\mathfrak g$}ngle l_{\gamma} {\rm p}gs \left( {\rm Ad}_{{\overline g}a^{-1}} X \right) ,
r_{\gamma^{-1}}^* Y\rangle \nonumber \\
&=& \mbox{$\mathfrak g$}ngle {\rm p}gs \left( {\rm Ad}_{{\overline g}a^{-1}} X \right) , {\rm Ad}_{{\overline g}a^{-1}}^* Y\rangle =
\mbox{$\mathfrak g$}ngle {\rm p}gs {\rm Ad}_{{\overline g}a^{-1}} X , {\rm p}g {\rm Ad}_{{\overline g}a^{-1}}
Y\rangle \nonumber \\
&=& \mbox{$\mathfrak g$}ngle{\rm p}i_{G^*} (\gamma), r^*_{\gamma^{-1}} (Y\wedge X)\rangle
{\rm e}quiv \mbox{$\mathfrak g$}ngle{\rm p}i_{G^*}^\sharp (r_{\gamma^{-1}}^* X),
r_{\gamma^{-1}}^* Y\rangle ~~\ .\nonumber
{\rm e}nd{eqnarray}
The proof for $\mathcal{S}_{\xi} (g)$ is similar.
{\rm e}nd{proof}
{\rm e}nd{lem}
The vector fields (\ref{dressing_vector_fields}) are called {{\rm i}t dressing vector fields}; their definition depends only on the
infinitesimal Lie bialgebra. Therefore they are defined even when ${\rm p}hi_1\times{\rm p}hi_2$ is not a diffeomorphism (and more generally
even if ${\rm p}hi_1$, ${\rm p}hi_2$ does not exist). We saw that if $D=G\times G^*$, then the dressing vector fields are complete. In
\cite{LuTh}, Lu has proved that $i$) the dressing vector fields of $G$ are complete if and only if those of $G^*$ are complete; $ii$)
$D=G\times G^*$ if and only if the dressing vector fields are complete.
Integrability of Poisson Lie groups has been shown in \cite{LW}. Let us consider the submanifold of $G\times G^*\times G^*\times G$ of dimension $2{\rm d}im G$ defined by
{\rm tr}gin{equation}\mbox{$\mathfrak g$}bel{sympl_grpd_noncomplete}
\Omega=\{(g_1,\gammamma_1,\gammamma_2,g_2){\rm i}n G\times G^*\times G^*\times G,\; {\overline g}_1{\overline g}a_1={\overline g}a_2 {\overline g}_2{\rm i}n D\}\;. {\rm e}nd{equation}
The local diffeomorphism ${{\mathfrak h}at P}i:\Omega\rightarrow D$, defined as ${{\mathfrak h}at P}i(g_1,\gammamma_1,\gammamma_2,g_2)={\overline g}_1{\overline g}a_1$, induces a nondegenerate Poisson structure on $\Omega$, that we still denote with ${\rm p}i_+$.
{\rm tr}gin{prop}\mbox{$\mathfrak g$}bel{sympl_gpd} Let $G$ be a connected and simply connected Poisson Lie group and let $G^*$ be the dual Poisson Lie group. Consider the groupoid ${\cal G}(G)=(\Omega,\mathit{a}lpha_G,{\rm tr}ta_G,m_G,{\rm e}psilon_G,i_G)$ over $G$ with structure maps:
{\rm tr}gin{itemize}
{\rm i}tem[i)] $\mathit{a}lphaG(g_1,\gammamma_1,\gammamma_2,g_2)=g_1$;
{\rm i}tem[ii)] ${\rm tr}taG(g_1,\gammamma_1,\gammamma_2,g_2)=g_2$;
{\rm i}tem[iii)] ${\rm e}psilon_{\mbox{\tiny G}}(g)=(g,e,e,g)$;
{\rm i}tem[iv)] $m_{\mbox{\tiny G}}[(g_1,\gammamma_1,\gammamma_2,g_2)(g_2,\mbox{$\mathfrak g$}mbda_1,\mbox{$\mathfrak g$}mbda_2,k_2)]=(g_1,\gammamma_1\mbox{$\mathfrak g$}mbda_1,\gammamma_2\mbox{$\mathfrak g$}mbda_2,k_2)$;
{\rm i}tem[v)] ${\rm i}ota_{\mbox{\tiny G}}(g_1,\gammamma_1,\gammamma_2,g_2)=(g_2,\gammamma^{-1}_1,\gammamma_2^{-1},g_1)$.
{\rm e}nd{itemize}
Then ${\cal G}(G)$ equipped with ${\rm p}i_+^{-1}$ is a symplectic groupoid integrating $(G,{\rm p}i_G)$.
Consider the groupoid
${\cal G}(G^*)=(\Omega,\mathit{a}lpha_{G^*},{\rm tr}ta_{G^*},m_{G^*},{\rm e}psilon_{G^*},i_{G^*})$ over $G^*$,
with structure maps:
{\rm tr}gin{itemize}
{\rm i}tem[i)] $\mathit{a}lphaGs(g_1,\gammamma_1,\gammamma_2,g_2)=\gammamma_2$;
{\rm i}tem[ii)] ${\rm tr}taGs(g_1,\gammamma_1,\gammamma_2,g_2)=\gammamma_1$;
{\rm i}tem[iii)] ${\rm e}psilon_{\mbox{\tiny G}^*}(\gammamma)=(e,\gammamma,\gammamma,e)$;
{\rm i}tem[iv)] $m_{\mbox{\tiny G}^*}[(g_1,\gammamma_1,\gammamma_2,g_2)(k_1,\mbox{$\mathfrak g$}mbda_1,\gammamma_1,k_2)]=(g_1k_1,\mbox{$\mathfrak g$}mbda_1,\gammamma_2,g_2k_2)$;
{\rm i}tem[v)] ${\rm i}ota_{\mbox{\tiny G}^*}(g_1,\gammamma_1,\gammamma_2,g_2)$ $=(g_1^{-1},\gammamma_2,\gammamma_1,g_2^{-1})$.
{\rm e}nd{itemize}
Then ${\cal G}(G^*)$ equipped with $-{\rm p}i_{+}^{-1}$ is a symplectic groupoid integrating $(G^*,{\rm p}i_{\mbox{\tiny G}^*})$.
{\rm e}nd{prop}
If $G$ and $G^*$ are complete, then $\Omega=G\times G^*$ globally and the above description can be given in terms of the dressing transformations. In particular the groupoid structures for ${\cal G}(G)$ read as $\mathit{a}lphaG(g\gammamma)=g$, ${\rm tr}taG(g\gammamma)=g^\gammamma$, $m_{\mbox{\tiny G}}[(g_1\gammamma_1)(g_1^{\gammamma_1}\gammamma_2)]=(g_1\gammamma_1\gammamma_2)$, ${\rm e}psilon_{\mbox{\tiny G}}(g)=(ge)$, ${\rm i}ota_{\mbox{\tiny G}}(g\gammamma)=g^\gammamma \gammamma^{-1}$. For ${\cal G}(G^*)$ we have $\mathit{a}lphaGs(g\gammamma)={}^g\gammamma$, ${\rm tr}taGs(g\gammamma)=\gammamma$, $m_{\mbox{\tiny G}^*}[(g_1{}^{g_2}\gammamma_2)(g_2\gammamma_2)]=(g_1g_2\gammamma_2)$, ${\rm e}psilon_{\mbox{\tiny G}^*}(\gammamma)=(e\gammamma)$, ${\rm i}ota_{\mbox{\tiny G}^*}(g\gammamma)=g^{-1}{}^g\gammamma$.
\subsection{The non simply connected case} Let us remove in this subsection the hypothesis that $G$ is simply connected. The above construction of the symplectic groupoid cannot be repeated since now ${\rm p}hi_1: {\tilde G}\rightarrow D$, where ${\tilde G}$ is the universal
covering of $G$. Let $Z\subset{\tilde G}$ be the discrete central subgroup such that $G={\tilde G}/Z$. There exists on ${\tilde G}$ a unique multiplicative
Poisson structure ${\rm p}i_{\tilde G}$ such that the quotient ${\tilde G}\rightarrow G$ is a Poisson map and ${\rm p}i_{\tilde G}(z)=0$ for any $z{\rm i}n Z$. As a
consequence the multiplication by $z$ on ${\tilde G}$ is a Poisson diffeomorphism; moreover by looking at (\ref{poisson_tensors}) we
see that since ${\rm p}i_{\tilde G}(z)=0$ we have ${\rm Ad}_{\overline z}\xi={\rm Ad}^*_z\xi$, for any $\xi{\rm i}n\mathfrak g^*$, and
${\rm Ad}_z^*\xi=\xi$ since $Z$ is central. So we can conclude that ${\rm p}hi_1(z)=\overline{z}$ commutes with ${\overline g}a$ for
any $\gammamma{\rm i}n G^*$ and that $Z$ acts as a symplectic groupoid morphism on the symplectic groupoid ${\cal G}({\tilde G})$ defined in
Proposition \ref{sympl_gpd} as $z(\tilde{g}_1,\gammamma_1,\gammamma_2,\tilde{g}_2)=(z\tilde{g}_1,\gammamma_1,\gammamma_2,z\tilde{g}_2)$.
{\rm tr}gin{prop}\mbox{$\mathfrak g$}bel{sympl_grpd_non1conn}
For any Poisson Lie group $G=\tilde{G}/ Z$, ${\cal G}(G)={\cal G}({\tilde G})/Z$ carries the structure of a symplectic groupoid integrating it.
{\rm e}nd{prop}
In the following we will denote the equivalence classes as $[\tilde{g}_1,\gammamma_1,\gammamma_2,\tilde{g}_2]{\rm i}n {\cal G}(G)$. Remark
that it can happen that ${\rm p}hi_1:\tilde{G}\rightarrow D$ satisfies ${\rm p}hi_1(Z)=1$ so that it descends to $G$. In this case it is possible to define a groupoid as in Proposition \ref{sympl_gpd}, even without assuming that $G$ is simply connected. It is
easily observed that such groupoid is a quotient by $Z$ of the groupoid defined in Proposition \ref{sympl_grpd_non1conn}.
As a simple consequence of Proposition \ref{sympl_gpd}, we have the following corollary.
{\rm tr}gin{cor} \mbox{$\mathfrak g$}bel{grpd_action} The symplectic groupoid ${\cal G}(G^*)$ acts simplectically on $\overline{{\cal G}(G)}$ with anchor $J:{\cal G}(G)\rightarrow G^*$ defined as $J[\tilde{g}_1,\gammamma_1,\gammamma_2,\tilde{g}_2]=\mathit{a}lphaGs(\tilde{g}_1,\gammamma_1,\gammamma_2,\tilde{g}_2)=\gammamma_2$; the action $a:{\cal G}(G^*){}_{\rm tr}taGs\!\times_J{\cal G}(G)\rightarrow {\cal G}(G)$ is given by
$$
a\{(\tilde{k}_1,\mbox{$\mathfrak g$}mbda_1,\mbox{$\mathfrak g$}mbda_2,\tilde{k}_2)[\tilde{g}_1,\gammamma_1,\mbox{$\mathfrak g$}mbda_1,\tilde{g}_2]\}=[\tilde{k}_1\tilde{g}_1,\gammamma_1,\mbox{$\mathfrak g$}mbda_2,\tilde{k}_2\tilde{g}_2]\;.
$$
{\rm e}nd{cor}
{\rm tr}gin{proof}
Simply observe that the graph of the action $a$ is the quotient under the action of $Z$ of the graph of the multiplication of ${\cal G}(G^*)$.
{\rm e}nd{proof}
In particular we have that $J:({\cal G}(G),{\rm p}i_+)\rightarrow (G^*,{\rm p}i_{\mbox{\tiny G}^*})$ is an anti-Poisson map.
\section{The symplectic groupoid of a homogeneous space}
In this section we discuss the integration of Poisson homogeneous spaces of the Poisson Lie group $G$.
Let us start with the simplest case of a Lie group $G$ with the zero Poisson structure ${\rm p}i_G=0$. Its symplectic groupoid ${\cal G}(G)=G\times \mathfrak{g}^\star$ is identified with the cotangent bundle after trivializing via left
translations. The left multiplication of $G$ on itself admits a cotangent lift $k(g,\xi)=(kg,\xi)$ for $k,g{\rm i}n G$ and $\xi{\rm i}n
\mathfrak{g}^\star$; this lifted action is hamiltonian with momentum map $J(g,\xi)={\rm Ad}^*_g(\xi)$. Let now $H$ be any closed
subgroup of $G$ with Lie algebra $\mathfrak h$. The restriction to $H$ of the lifted action is again obviously hamiltonian with
momentum map ${J_{\mbox{\tiny H}}}={\rm pr}_H\circ J$, where ${\rm pr}_H:{\mathfrak g}^\star\rightarrow {\mathfrak g}^\star/{\mathfrak h}^{\rm p}erp$ and $\mathfrak{h}^{\rm p}erp = \{ \xi {\rm i}n g^\star:~ \mbox{$\mathfrak g$}ngle\xi, X\rangle=0, \forall X {\rm i}n \mbox{${\mathfrak h}$} \}$.
The symplectic groupoid of the quotient is just the Marsden--Weinstein reduction of this hamiltonian action: $T^*(H\backslash
G)=H\backslash {J_{\mbox{\tiny H}}}^{-1}(0)$.
We are going to see how this generalizes to a generic Poisson Lie group. We know that any action by Poisson diffeomorphism on an
integrable Poisson manifold can be lifted to a hamiltonian action on the (ssc) symplectic groupoid with a multiplicative momentum
map, see \cite{MW,FOR}. This construction applies only to the case $H$ being a Poisson subgroup with zero Poisson structure; it is
clear that in the general case one has to consider generalized notions of hamiltonian actions and even in the generalized setting
we will consider, the lifting property will not be automatic.
\subsection{Embeddable homogeneous spaces}
Let us recall some basic facts about coisotropic subgroups and their role in the quotient of Poisson manifolds. Let $H$ be a coisotropic connected closed subgroup of the Poisson Lie group $G$ and $\mathfrak{h} = Lie~H$. At the infinitesimal level, coisotropic subgroups are characterized by the following Proposition, whose proof can be found in \cite{STT}.
{\rm tr}gin{prop} \mbox{$\mathfrak g$}bel{thm_coi_alg}
A subgroup $H$ is coisotropic if and only if $\mathfrak{h}^{\rm p}erp \subset \mbox{${\mathfrak g}$}^\star$ is a subalgebra of $\mbox{${\mathfrak g}$}^\star$, where $\mathfrak{h}^{\rm p}erp = \{ \xi {\rm i}n g^\star:~ \mbox{$\mathfrak g$}ngle\xi, X\rangle=0, \forall X {\rm i}n \mbox{${\mathfrak h}$} \}$.
{\rm e}nd{prop}
\noindent{\bf Assumption}: Let $\mathfrak{h}^{\rm p}erp$ be integrated by a closed subgroup $H^{\rm p}erp \subset G^*$.
As a consequence of Proposition \ref{thm_coi_alg}, $H^{\rm p}erp$ results coisotropic as well. The following property of coisotropic subgroups will be relevant in what follows.
{\rm tr}gin{lem} \mbox{$\mathfrak g$}bel{lem_h_hperp_inacca}
Given a coisotropic subgroup $H \subset G$, then the restriction of the (infinitesimal) dressing actions of $G$ on $G^*$ to $H$ leaves $H^{\rm p}erp$ invariant and its orbits are the coisotropic leaves. Moreover, when $H$ is a Poisson subgroup, then the dressing action of $H^{\rm p}erp$ on $H$ is trivial.
{\rm e}nd{lem}
{\rm tr}gin{proof}
Since for any $\gammamma{\rm i}n H^{\rm p}erp$ we can characterize $T_\gammamma H^{\rm p}erp$ as $r_\gammamma{\mathfrak h}^{\rm p}erp$, we get that $N^*_\gammamma H^{\rm p}erp=r^*_{\gammamma^{-1}}{\mathfrak h}$. Then the dressing vector fields $\mathcal{S}_{X} (\gamma) = {\rm p}i_{\mbox{\tiny G}^*}^\sharp (r_{\gamma^{-1}}^* X)$ corresponding to $X{\rm i}n{\mathfrak h}$ (see Lemma \ref{lem_fund_vec}) span the coisotropic distribution and, in particular, are tangent to $H^{\rm p}erp$.
Analogously for the right dressing action. To prove the last statement, let us recall
that the coisotropic foliation of a Poisson submanifold is null. {\rm e}nd{proof}
{\rm tr}gin{cor}
If $H$ is a Poisson subgroup, then $H$ acts on $H^{\rm p}erp$ by automorphisms.
{\rm e}nd{cor}
{\rm tr}gin{proof}
Let us prove it in the complete case. Let $h{\rm i}n H$, $\gammamma_i{\rm i}n H^{\rm p}erp$. By the properties (\ref{properties_dressing}) of the dressing action, ${}^h (\gamma_1 \gamma_2) = {}^h \gamma_1 ~~ {}^{h^{\gamma_1}} \gamma_2$. As $h^{\gamma_1} = h$ by means of Lemma \ref{lem_h_hperp_inacca}, then ${}^h (\gamma_1 \gamma_2) = {}^h \gamma_1 ~~ {}^h \gamma_2$. In the general case, infinitesimal action by automorphisms means that the dressing vector fields of $H$ on $H^{\rm p}erp$ are multiplicative.
{\rm e}nd{proof}
Let us denote with $\tilde{H}$, $\tilde{G}$ the universal covers of $H$ and $G$ respectively and let ${\rm p}hi_{\tilde{H}}:\tilde{H}\rightarrow {\tilde G}$ the group homomorphism integrating the inclusion $\mathfrak{h}\rightarrow\mathfrak{g}$. Then let us define
{\rm tr}gin{equation}\mbox{$\mathfrak g$}bel{subgroupoidofH}
\Omega(\tilde{H},H^{\rm p}erp) = \{({\rm p}hi_{\tilde H}(\tilde{h}_1),\gammamma_1,\gammamma_2,{\rm p}hi_{\tilde H}(\tilde{h}_2)){\rm i}n{\cal G}({\tilde G}),\; \tilde{h}_i{\rm i}n\tilde{H},\, \gammamma_i{\rm i}n H^{\rm p}erp\}\subset \Omega\;.
{\rm e}nd{equation}
It is clear that $\Omega(\tilde{H},H^{\rm p}erp)$ defines a subgroupoid ${\cal G}({\tilde G},{\rm p}hi_{\tilde{H}}({\tilde H}))$ over ${\rm p}hi_{\tilde H}({\tilde H})$ of ${\cal G}({\tilde G})$ and a subgroupoid ${\cal G}(G^*,H^{\rm p}erp)$ over $H^{\rm p}erp$ of ${\cal G}(G^*)$. They respectively integrate the subalgebroids $N^*{\rm p}hi_{\tilde{H}}({\tilde H})\subset T^*{\tilde G}$ and $N^*H^{\rm p}erp\subset T^*G^*$.
The following theorem establishes the role of coisotropic subgroups in the quotient of Poisson manifolds (the proof can be found in \cite{LuTh}).
{\rm tr}gin{thm}
\mbox{$\mathfrak g$}bel{thm_poi_red}
Let $\sigma: K \times P \rightarrow P$ be a Poisson action of the Poisson Lie group $K$ over the Poisson manifold $P$ and let $B \subset K$ be a coisotropic subgroup of $K$. If the orbit space $B \backslash P$ is a smooth manifold, then there is a unique Poisson structure on $B \backslash P$ such that the natural projection map $P \rightarrow B \backslash P$ is Poisson.
{\rm e}nd{thm}
Let $H$ be a coisotropic subgroup of the Poisson Lie group $G$; if we apply this result to $P=K=G$, $B=H$ and to $P=K=G^*$, $B=H^{\rm p}erp$ we conclude that both $H\backslash G$ and $G^*/H^{\rm p}erp$ are Poisson manifolds.
Borrowing the terminology from quantum groups we call them {{\rm i}t embeddable Poisson homogeneous spaces}, since $H$-invariant functions on $G$ are a Poisson subalgebra of $C^{\rm i}nfty(G)$. Let ${\rm p}h : G \rightarrow H \backslash G$ and ${\rm p}hp: G^*\rightarrow G^*/H^{\rm p}erp$ the projection maps and let us denote ${\rm p}h(g)=\underline{g}$ and ${\rm p}hp(\gammamma)=\underline{\gammamma}$.
Embeddable Poisson homogeneous spaces come with a distinct point, the image $\underline{e}$ of the identity $e$, where the coinduced Poisson structure vanishes. Indeed, they can be characterized as those having at least one point where the Poisson structure vanishes, or equivalently the stability group of such a point is coisotropic.
\subsection{The complete and simply connected case}
Let us assume that $G$ is simply connected and complete. Let us review the concept of symplectic reduction via Lu's momentum map.
{\rm tr}gin{dfn} \mbox{$\mathfrak g$}bel{dfn_momap}
A $C^{{\rm i}nfty}$ map $J: P \rightarrow G^*$ is called a momentum mapping for the left Poisson action $\sigma: G\times P\rightarrow P $ if
\[
\sigma_{\mbox{\tiny X}} ~ = ~ - {\rm p}i_{\mbox{\tiny P}}^\sharp
(J^{*}(\mbox{$X^{r}$})), ~~~ \forall X {\rm i}n \mbox{$\mathfrak g$}.
\]
where for each $X {\rm i}n \mbox{$\mathfrak g$}$, $\mbox{$X^{r}$}$ is the right invariant $\mbox{$1$-form}$ on $\mbox{$G^{*}$}$ with value $X$ at $e$, and $\sigma_{\mbox{\tiny X}}$ is the fundamental vector field associated to $X$ by the action $\sigma$. The momentum mapping $J$ is said to be equivariant if $J(\sigma(g,p))={}^g(J(p))$, for any $g{\rm i}n G$ and $p{\rm i}n P$.
{\rm e}nd{dfn}
Remark that this definition is slightly different from the one given in \cite{LuTh}. If $P$ is symplectic, a Poisson action $\sigma$ admits a momentum mapping $J$ if and only if there exists a symplectic action of the symplectic groupoid ${\cal G}(G^*)$ on $P$ with anchor $J$: the correspondence is given by $\sigma(g,p)=(gJ(p))p$, for $g{\rm i}n G$, $p{\rm i}n P$, see \cite{WX}. Remark that this correspondence demands $G$ to be complete. By applying this result to $P={\cal G}(G)$ we get that the left $G$-action on ${\cal G}(G)$ given by $\sigma(g,(k\gammamma))=gk\gammamma$ is Poisson and admits an equivariant momentum mapping $J(g\gammamma)={}^g\gammamma$. Moreover it is multiplicative, {{\rm i}t i.e.} if $(g_1\gammamma_1)$ and $(g_2\gammamma_2)$ are composable then $J((g_1\gammamma_1)(g_2\gammamma_2))=J(g_1\gammamma_1)J(g_2\gammamma_2)$.
More concretely, for any $X{\rm i}n\mbox{$\mathfrak g$}$, the fundamental vector field of the left $G$-action is $\sigma_X(g\gammamma)=r_{(g\gammamma)^{-1}*}X$ and the right invariant form $X^r_\gammamma=r^*_{\gammamma^{-1}}X$. We have that, for any $g\gammamma{\rm i}n{\cal G}(G)$,
{\rm tr}gin{equation}\mbox{$\mathfrak g$}bel{lem_momap_poi_ac}
\sigma_X(g\gammamma)=-{\pi_+^\sharp}\circ [T_{g\gammamma} J]^* (X^r_{J(g\gammamma)})\;.
{\rm e}nd{equation}
Let us introduce the map
{\rm tr}gin{equation}\mbox{$\mathfrak g$}bel{momentum_map}
{J_{\mbox{\tiny H}}} = {\rm p}hp \circ J,~~~~~ {J_{\mbox{\tiny H}}}(g\gammamma)=\underline{{}^g\gammamma}.
{\rm e}nd{equation}
Being a composition of Poisson submersions, ${J_{\mbox{\tiny H}}}$ is a Poisson submersion too. In the special case in which $H$ is a Poisson Lie subgroup, $H^{\rm p}erp$ is a normal subgroup and $G^*/H^{\rm p}erp{\rm e}quiv H^*$ is a Poisson Lie group with Lie algebra ${\mathfrak h}^\star=\mbox{$\mathfrak g$}^\star/{\mathfrak h}^{\rm p}erp$. By using (\ref{properties_dressing}) it can be easily shown that the dressing action of $H$ descends to $G^*/H^{\rm p}erp$, ${}^h{\rm p}hp(\gammamma){\rm e}quiv{\rm p}hp({}^h\gammamma)$, for any $h{\rm i}n H$ and $\gammamma{\rm i}n G^*$. Then ${J_{\mbox{\tiny H}}}$ is an equivariant and multiplicative momentum mapping for the left multiplication by $H$. In the general coisotropic case, $G^*/H^{\rm p}erp$ is only a Poisson manifold and ${J_{\mbox{\tiny H}}}$ must be thought as a momentum mapping in a generalized sense, see Corollary \ref{gpd_gpd_red} at the end of this subsection.
Let us consider ${J_{\mbox{\tiny H}}}^{-1} (\underline{e})=\{g\gamma{\rm i}n G \times G^*:{}^g \gamma {\rm i}n H^{\rm p}erp\}$, that is a submanifold since ${J_{\mbox{\tiny H}}}$ is a submersion. Since $\{\underline{e}\}$ is a zero dimensional leaf of $G^*/H^{\rm p}erp$ then ${J_{\mbox{\tiny H}}}^{-1} (\underline{e})$ is coisotropic in $G \times G^*$. Let us show that the left multiplication by $H$ leaves ${J_{\mbox{\tiny H}}}^{-1} (\underline{e})$ invariant: Lemma \ref{lem_h_hperp_inacca} implies that, if $g\gamma {\rm i}n J_{\mbox{\tiny H}}^{-1} (\underline{e})$, that is if ${}^g \gamma {\rm i}n H^{\rm p}erp$, then ${}^{h g} \gamma {\rm e}quiv {}^h ({}^g \gamma) {\rm i}n {}^h (H^{\rm p}erp) = H^{\rm p}erp$, and then $h g \gamma {\rm i}n J_{\mbox{\tiny H}}^{-1} (\underline{e})$. The left $H$ action is proper and free so that the orbit space is smooth.
{\rm tr}gin{thm} \mbox{$\mathfrak g$}bel{thm_groupoid}
$\mathcal{G} (H\backslash G) = H\backslash {J_{\mbox{\tiny H}}}^{-1} (\underline{e})$ is a symplectic groupoid that integrates $H\backslash G$.
{\rm e}nd{thm}
{\rm tr}gin{proof} Since $J_{\mbox{\tiny H}}^{-1} (\underline{e})$ is a coisotropic submanifold of $\mathcal{G} (G)$, it admits a symplectic reduction and let $\mbox{$\omega$}ega_+^H$ the induced symplectic structure. Let us show that this reduction coincides with the quotient by the left $H$ action. Formula \ref{lem_momap_poi_ac} implies that the fundamental vector fields associated to the left multiplication of $G \times G^*$ by $H$ are given by
{\rm tr}gin{equation}\mbox{$\mathfrak g$}bel{actionofH}
\sigma_{\mbox {\tiny X}} (g \gamma) = -{\rm p}i_{\mbox{\tiny +}}^\sharp \left[ [T_{g \gamma} J]^* \circ r_{J(g \gamma)^{-1}}^* X \right], ~~~ \forall X {\rm i}n \mbox{${\mathfrak h}$},
{\rm e}nd{equation}
where we recall that $J : \mathcal{G}(G) \rightarrow G^* : g\gamma \mapsto {}^g \gamma$ is the momentum mapping. On the other hand, the coisotropic distribution is defined as
\[
{\rm p}i_{\mbox{\tiny +}}^\sharp \left( N^*_{g \gamma} J_{\mbox{\tiny H}}^{-1} (\underline{e}) \right),~~~ \forall g \gamma {\rm i}n J_{\mbox{\tiny H}}^{-1} (\underline{e}).
\]
Simple identities allow to write for $g\gammamma{\rm i}n{J_{\mbox{\tiny H}}}^{-1}(\underline{e})$
{\rm tr}gin{eqnarray*}
N^*_{g \gamma} {J_{\mbox{\tiny H}}}^{-1} (\underline{e}) &=& {\rm Ker} [T_{g \gamma} {J_{\mbox{\tiny H}}}]^{\rm p}erp ={\rm Im}[T_{g\gammamma} {J_{\mbox{\tiny H}}}]^* =\{[T_{g \gamma} J]^* \circ [T_{J(g \gamma)} p_{\mbox{\tiny H}^{\rm p}erp} ]^* X, ~~~ \forall X {\rm i}n \mbox{${\mathfrak h}$} \} \cr
&=& \{[T_{g \gamma} J]^* \circ r^*_{J(g\gammamma)^{-1}}X, ~~~ \forall X {\rm i}n \mbox{${\mathfrak h}$} \},
{\rm e}nd{eqnarray*}
since ${\rm p}hp\circ r_{J(g\gammamma)^{-1}}={\rm p}hp$ and $[T_e{\rm p}hp]^*:T^*_{\underline e} (G^*/H^{\rm p}erp){\rm e}quiv\mbox{${\mathfrak h}$}\rightarrow T^*_eG^*{\rm e}quiv\mbox{$\mathfrak g$}$ is just the inclusion map.
Let us show that $J_{\mbox{\tiny H}}^{-1} (\underline{e})$ is a subgroupoid of $\mathcal{G}(G)$.
Take $g_1\gamma_1,g_2\gamma_2 {\rm i}n J_{\mbox{\tiny H}}^{-1} (\underline{e})$ such that $g_2 = g_1^{\gamma_1}$. Then $m(g_1\gamma_1,g_2\gamma_2) = g_1 \gamma_1 \gamma_2 {\rm i}n J_{\mbox{\tiny H}}^{-1} (\underline{e})$ since ${}^{g_1} (\gamma_1 \gamma_2) = {}^{g_1} \gamma_1 ~ {}^{g_1^{\gamma_1}} \gamma_2 {\rm i}n H^{\rm p}erp$ because ${}^{g_1^{\gamma_1}} \gamma_2 = {}^{g_2} \gamma_2 {\rm i}n H^{\rm p}erp$ by definition. The quotient $H\backslash {J_{\mbox{\tiny H}}}^{-1} (\underline{e})$ inherits the structure of groupoid. In fact the left $H$ action on ${J_{\mbox{\tiny H}}}^{-1}(\underline{e})$ and on $G$ defines the relations $S_H\subset {J_{\mbox{\tiny H}}}^{-1}(\underline{e})\times {J_{\mbox{\tiny H}}}^{-1}(\underline{e})$ and $R_H\subset G\times G$, respectively; one can show that $(S_H,R_H)$ is a smooth congruence on ${J_{\mbox{\tiny H}}}^{-1}(\underline{e})$, according to Definition 2.4.5 of \cite{MK}, that induces a unique Lie groupoid structure on the quotient. We will follow a more direct way, by explicitly defining this groupoid structure. Let us denote with $\underline{g}{\rm i}n H\backslash G$ the equivalence class of $g{\rm i}n G$ and with $\underline{g}\gammamma$ the equivalence class of $g\gammamma{\rm i}n {J_{\mbox{\tiny H}}}^{-1}(\underline{e})$. The source and target maps are defined as
{\rm tr}gin{eqnarray}
\mathit{a}lphaGH (\underline{g} \gamma) &=& \underline {\mathit{a}lpha_{\mbox{\tiny G}} (g \gamma)} = \underline {g} \nonumber \\
{\rm tr}taGH (\underline{g}\gamma) &=& \underline{{\rm tr}ta_{\mbox{\tiny G}}(g \gamma)} = \underline {g^\gamma} \;; \nonumber
{\rm e}nd{eqnarray}
one must check that the definition of ${\rm tr}taGH$ is correct; indeed ${\rm tr}taGH (\underline{h g} \gamma) = \underline{(h g)^\gamma} = \underline{h^{{}^{g} \gamma} ~ g^\gamma}=\underline {g^\gamma}$ since ${}^{g} \gamma {\rm i}n H^{\rm p}erp$. Given $\underline{g_i} \gamma_i {\rm i}n H \backslash {J_{\mbox{\tiny H}}}^{-1}(\underline{e})$,
$i = 1, 2$, such as $\mathit{a}lphaGH (\underline{g_2} \gamma_2) = \underline{g_2} = \underline {g_1^{\gamma_1}} = {\rm tr}taGH (\underline{g_1} \gamma_1)$, we set ${{\rm m}_{\mbox{\tiny G}}^{\mbox{\tiny H}}}(\underline{g_1} \gamma_1 , \underline{g_2} \gamma_2)=
\underline{g_1} \gamma_1 \gamma_2$. Then $\mathit{a}lphaGH ( \underline{g_1} \gamma_1 \gamma_2 ) = \underline{g_1} =
\mathit{a}lphaGH ( \underline{g_1} \gamma_1 )$ and ${\rm tr}taGH ( \underline{g_1} \gamma_1 \gamma_2) =
\underline{g_1^{\gamma_1\gamma_2}} = \underline{(h g_2)^{\gamma_2}} =\underline{h^{{}^{g_2} \gamma_2} ~ {g_2^{\gamma_2}}}=
{\rm tr}taGH (\underline{g_2} \gamma_2)$, where $h {\rm i}n H$ is such that $h g_2 =
g_1^{\gamma_1}$, which follows from the condition of composability, and last equality follows, once more, from the condition that ${}^{g_2}\gammamma_2{\rm i}n H^{\rm p}erp$.
Finally, let us show that the reduced symplectic form $\mbox{$\omega$}ega_+^H$ is multiplicative. First, we observe that the restriction of $\mbox{$\omega$}ega_+={\rm p}i_+^{-1}$ to ${J_{\mbox{\tiny H}}}^{-1}(\underline{e})$ is multiplicative, making it a presymplectic groupoid. Then we observe that the quotient map ${\rm p}h^{(1)}:{J_{\mbox{\tiny H}}}^{-1}(\underline{e})\rightarrow {\cal G}(H\backslash G)$ induces a submersion ${\rm p}h^{(2)}:{J_{\mbox{\tiny H}}}^{-1}(\underline{e})^{(2)}\rightarrow{\cal G}(H\backslash G)^{(2)}$, so that any element in $\Lambdambda^2 T{\cal G}(H\backslash G)^{(2)}$ can be written as ${\rm p}h_*^{(2)}V$ for $V{\rm i}n \Lambdambda^2 T{J_{\mbox{\tiny H}}}^{-1}(\underline{e})^{(2)}$. We then have
$$
\mbox{$\mathfrak g$}ngle ({{\rm m}_{\mbox{\tiny G}}^{\mbox{\tiny H}}}^*-{\rm p}rGHuno^* - {\rm p}rGHdue^*)\mbox{$\omega$}ega_+^H,{\rm p}h_*^{(2)} V\rangle = \mbox{$\mathfrak g$}ngle (m^*-{\rm p}runo^*-{\rm p}rdue^*)\mbox{$\omega$}ega_+,V \rangle = 0\;.
$$
{\rm e}nd{proof}
One can think of this reduction as a reduction of a symplectic groupoid action. Let ${\cal G}(G^*/H^{\rm p}erp)$ the symplectic groupoid integrating $G^*/H^{\rm p}erp$ obtained by the right counterpart of the above procedure. In total analogy with the above construction we have that ${\cal G}(G^*/H^{\rm p}erp)=\{g\underline{\gammamma}{\rm i}n G^*\times G^*/H^{\rm p}erp, \; g^\gammamma{\rm i}n H\}$. The groupoid structures are $\mathit{a}lphaGsHp(g\underline{\gammamma})=\underline{{}^g\gammamma}$, ${\rm tr}taGsHp(g\underline{\gammamma})=\underline{\gammamma}$, ${{\rm m}_{\mbox{\tiny G}^*}^{\mbox{\tiny H}^\perp}}[(g_1\underline{\gammamma_1})(g_2\underline{\gammamma_2})]=g_1g_2\underline{\gammamma_2}$ for $\underline{\gammamma_1}=\underline{{}^{g_2}\gammamma_2}$, etc... It is also clear that the isotropy group of $\underline{e}$ is ${\cal G}(G^*/H^{\rm p}erp)^{\underline{e}}_{\underline{e}}=H$. One can easily check that ${J_{\mbox{\tiny H}}}:{\cal G}(G)\rightarrow G^*/H^{\rm p}erp$ is the anchor for the symplectic action of ${\cal G}(G^*/H^{\rm p}erp)$ on ${\cal G}(G)$ given by $(k\underline{\mbox{$\mathfrak g$}mbda})(g\gammamma)=kg\gammamma$.
{\rm tr}gin{cor}\mbox{$\mathfrak g$}bel{gpd_gpd_red}
${\cal G}(H\backslash G) = {\cal G}(G^*/H^{\rm p}erp)^{\underline{e}}_{\underline{e}}\backslash{J_{\mbox{\tiny H}}}^{-1}(\underline{e})$\;.
{\rm e}nd{cor}
\subsection{The general case}\mbox{$\mathfrak g$}bel{generalcase} If $G$ is neither complete nor simply connected, we have to use
the general form of ${\cal G}(G)$ given in Proposition \ref{sympl_grpd_non1conn}. Most of the construction of the
complete and simply connected case can be generalized in a straightforward way, apart from few crucial facts. Instead of Lu's
momentum map, we have to think of ${\cal G}(G)$ as a hamiltonian ${\cal G}(G^*)$ space, as described in Corollary \ref{grpd_action}. In
particular, the map ${J_{\mbox{\tiny H}}}$ defined as in (\ref{momentum_map}) is still a Poisson submersion and ${J_{\mbox{\tiny H}}}^{-1}(\underline{e})$ is a
coisotropic submanifold of ${\cal G}(G)$. The coisotropic reduction is therefore well defined. First of all, care has to be taken about smoothness of this quotient. In fact, in the general case the ${\cal G}(G^*)$-action of Corollary \ref{grpd_action} does not define a left $G$-action, due to non completeness of dressing vector fields. In particular, formula (\ref{actionofH}) still defines an infinitesimal action of $\mathfrak{h}$, spanning the coisotropic distribution, that cannot
in general be integrated to a group action of $H$.
We first remark that it can be integrated to a groupoid action. In fact the restriction of the groupoid action $a:{\cal G}(G^*){}_{\rm tr}taGs\!\times_J{\cal G}(G)\rightarrow {\cal G}(G)$ defined in Corollary \ref{grpd_action} to the subgroupoid ${\cal G}(G^*,H^{\rm p}erp)$ defined in (\ref{subgroupoidofH}) leaves ${J_{\mbox{\tiny H}}}^{-1}(\underline{e})$ invariant, {{\rm i}t i.e.} we have a left groupoid action $a:{\cal G}(G^*,H^{\rm p}erp){}_{\rm tr}taGs\!\!\times_J{J_{\mbox{\tiny H}}}^{-1}(\underline{e})\rightarrow{J_{\mbox{\tiny H}}}^{-1}(\underline{e})$ with anchor $J:{J_{\mbox{\tiny H}}}^{-1}(\underline{e})\rightarrow H^{\rm p}erp$. Furthermore, its infinitesimal action is the restriction of the algebroid action of $T^*G^*$ on ${\cal G}(G)$, and by repeating the argument in the proof of Theorem \ref{thm_groupoid}, spans the coisotropic distribution of ${J_{\mbox{\tiny H}}}^{-1}(\underline{e})$. The coisotropic quotient can be obtained as ${\cal G}(G^*,H^{\rm p}erp)\backslash {J_{\mbox{\tiny H}}}^{-1}({\underline e})$, the orbit space of the groupoid action of ${\cal G}(G^*,H^{\rm p}erp)$. Although ${J_{\mbox{\tiny H}}}^{-1}(\underline{e})$ is still a subgroupoid of ${\cal G}(G)$, it is not obvious a priori that this groupoid action defines a smooth congruence in ${J_{\mbox{\tiny H}}}^{-1}({\underline e})$ and so a groupoid structure on the quotient.
In order to overcome these problems, we introduce a weaker notion of completeness of dressing vector fields reducing the problem to a quotient by an ordinary free and proper group action. We say that two Lie algebras $(\mathfrak{g}_1,\mathfrak{g}_2)$
are a {{\rm i}t matched pair of Lie algebras} if there exists a third Lie algebra ${\mathfrak g}_1\bowtie{\mathfrak g}_2$, called the {{\rm i}t double Lie algebra}, isomorphic to ${\mathfrak g}_1\mbox{$\Omega^{1}(P)$}lus{\mathfrak g}_2$ as vector space and containing ${\mathfrak g}_1$ and ${\mathfrak g}_2$ as Lie subalgebras. It comes out that $a$ and $b$ defined by $[X,\xi]=b_\xi(X)\mbox{$\Omega^{1}(P)$}lus a_X(\xi)$ for $X{\rm i}n {\mathfrak g}_1$, $\xi{\rm i}n{\mathfrak g}_2 $, define compatible actions of the two Lie algebras on each other.
Accordingly, we say that two Lie groups $G_1$ and $G_2$ form {{\rm i}t a matched pair of Lie groups} if there exists a third Lie group $G_1\bowtie G_2$, called the {{\rm i}t double Lie group}, diffeomorphic to $G_1\times G_2$ and containing $G_1$ and $G_2$ as closed Lie subgroups. It comes out that $G_1$ and $G_2$ act on each other with actions satisfying compatibility conditions analogue to (\ref{properties_dressing}); viceversa, given such compatible actions then there exists a unique double Lie group (see \cite{Mj}, \cite{LW2}).
It is clear that the couples $({\mathfrak g},{\mathfrak g}^\star)$ and $(\mathfrak{h},\mathfrak{h}^{\rm p}erp)$ form matched pairs of Lie algebras with the coadjoint actions as compatible actions. We say that $(H,H^{\rm p}erp)$ are
{{\rm i}t relatively complete} if the infinitesimal actions of $\mathfrak{h}$ on $H^{\rm p}erp$ and of $\mathfrak{h}^{\rm p}erp$ on $H$ via
the dressing vector fields can be integrated in such a way that $(H,H^{\rm p}erp)$ forms a matched pair of Lie groups, or equivalently that
the finite actions of $H$ and $H^{\rm p}erp$ satisfy relations (\ref{properties_dressing}). We need the following Lemma concerning the universal cover of $H$, in order to include the case when $G$ is not simply connected.
{\rm tr}gin{lem}\mbox{$\mathfrak g$}bel{lift_dressing_univ_cover}
{\rm tr}gin{itemize}
{\rm i}tem[$i$)] If $(H,H^{\rm p}erp)$ forms a matched pair of Lie groups then also $(\tilde{H},H^{\rm p}erp)$ forms a matched pair,
where $\tilde{H}$ is the universal cover of $H=\tilde{H}/Z_H$.
{\rm i}tem[$ii$)] The center $Z_H\subset\tilde{H}$ acts trivially on $H^{\rm p}erp$ and is a fixed point set of the dressing action of $H^{\rm p}erp$.
{\rm i}tem[$iii$)] The quotient map $\tilde{H}\rightarrow H$ intertwines the $H^{\rm p}erp$ action, {{\rm i}t i.e.} $\tilde{h}^\gammamma\rightarrow h^\gammamma$ for any lift $\tilde{h}$ of $h{\rm i}n H$ and $\gammamma{\rm i}n H^{\rm p}erp$.
{\rm e}nd{itemize}
{\rm e}nd{lem}
{\rm tr}gin{proof}
Let us prove point $i$). Any $\tilde{h}{\rm i}n\tilde{H}$ can be seen as the equivalence class $[h]$ of a path $h:[0,1]\rightarrow H$, with $h(0)=e$, with respect to homotopies preserving end points. Since $H^{\rm p}erp$ is connected and its action on $H$ preserves the identity, for any $\gammamma{\rm i}n H^{\rm p}erp$ and $[h]{\rm i}n\tilde{H}$, define the action of $H^{\rm p}erp$ on $\tilde{H}$ as $[h]^\gammamma=[h^\gammamma]$, where
$h^\gammamma(t)=h(t)^\gammamma$, and the action of $\tilde{H}$ on $H^{\rm p}erp$ as ${}^{[h]}\gammamma={}^{h(1)}\gammamma$. It is immediate to
check that they are well defined and that ${}^{[h]}(\gammamma_1\gammamma_2)={}^{[h]}\gammamma_1 {}^{[h]^{\gammamma_1}}\gammamma_2$. In order to check that $([h_1][h_2])^\gammamma=[h_1]^{{}^{[h_2]}\gammamma}[h_2]^\gammamma$ we have to prove that the paths $t\rightarrow h_1(t)^{ {}^{h_2(t)}\gammamma}$
and $t\rightarrow h_1(t)^{{}^{h_2(1)}\gammamma}$ are homotopic. This can be shown by using the homotopy $F(s,t)=h_1(t)^{{}^{h_2(t+s(1-t))} \gammamma}$.
In order to get point $ii$), we observe that $Z_H={\rm p}i_1(H)$ is realized as homotopy classes of loops and its action on $H^{\rm p}erp$ is trivial; the action of $H^{\rm p}erp$ on $Z_H$ is trivial since $H^{\rm p}erp$ is connected to the identity so that any loop $z$ is homotopic to $z^\gammamma$. Finally, point $iii$) can be directly verified once one realizes that the quotient $\tilde{H}\rightarrow H$ is realized as $[h]\rightarrow h(1)$.
{\rm e}nd{proof}
Let $\tilde{H}\bowtie H^{\rm p}erp$ be the double Lie group with the product rule given by $\tilde{h}\gammamma={}^{\tilde{h}}\gammamma \tilde{h}^\gammamma$, for $\tilde{h}{\rm i}n \tilde{H}$ and $\gammamma{\rm i}n H^{\rm p}erp$.
{\rm tr}gin{thm}
\mbox{$\mathfrak g$}bel{thm_groupoid_general} If $(H,H^{\rm p}erp)$ are relatively complete then the left groupoid action $a:{\cal G}(G^*,H^{\rm p}erp)$ ${}_{\rm tr}taGs\!\!\times_J{J_{\mbox{\tiny H}}}^{-1}(\underline{e})\rightarrow{J_{\mbox{\tiny H}}}^{-1}(\underline{e})$ is equivalent to a free and proper action of $H$ and $H\backslash{J_{\mbox{\tiny H}}}^{-1}(\underline{e})$ is a symplectic groupoid that integrates $H\backslash G$.
{\rm e}nd{thm}
{\rm tr}gin{proof}
Let ${\tilde G}$ be the universal covering of $G$ so that $G={\tilde G}/Z$ and let ${\cal G}(G)=Z\backslash{\cal G}({\tilde G})$ be as described in Proposition \ref{sympl_grpd_non1conn}. Let us recall that ${\rm p}hi_1:{\tilde G}\rightarrow D$ and ${\rm p}hi_2:G^*\rightarrow D$ are the Lie group homomorphisms entering the definition of ${\cal G}({\tilde G})$.
We have that $[\tilde{g}_1,\gammamma_1,\gammamma_2,\tilde{g}_2]{\rm i}n {J_{\mbox{\tiny H}}}^{-1}(\underline{e})$ if $\gammamma_2{\rm i}n H^{\rm p}erp$. Let ${\rm p}hi_{\tilde H}:\tilde{H}\rightarrow{\tilde G}$ be the Lie group homomorphism induced by the injection ${\mathfrak h}\rightarrow {\mathfrak g}$. Then we have that ${\rm p}hi_{\tilde{H}}(Z_H)\subset Z$.
Moreover, due to the uniqueness of the group homomorphism integrating any Lie algebra morphism, we can conclude that ${\rm p}si:\tilde{H}\bowtie H^{\rm p}erp\rightarrow D$ defined as ${\rm p}si(\tilde{h}\gammamma)={\rm p}hi_1({\rm p}hi_{\tilde{H}}(\tilde{h})){\rm p}hi_2(\gammamma)$, for $\tilde{h}{\rm i}n\tilde{H}$ and $\gammamma{\rm i}n H^{\rm p}erp$, is a group homomorphism. For any $\tilde{h}{\rm i}n\tilde{H}$, $\mbox{$\mathfrak g$}mbda{\rm i}n H^{\rm p}erp$ we have that $({\rm p}hi_{\tilde{H}}(\tilde{h}),\mbox{$\mathfrak g$}mbda,{}^{\tilde{h}}\mbox{$\mathfrak g$}mbda,{\rm p}hi_{\tilde{H}}(\tilde{h}^\mbox{$\mathfrak g$}mbda)){\rm i}n{\cal G}(G^*,H^{\rm p}erp)$. In fact, by using the definition above of ${\rm p}si$ we have
{\rm tr}gin{eqnarray}\nonumber
{\rm p}hi_1({\rm p}hi_{\tilde{H}}(\tilde{h})){\rm p}hi_2(\mbox{$\mathfrak g$}mbda)&=&{\rm p}si(\tilde{h}\mbox{$\mathfrak g$}mbda)=
{\rm p}si({}^{\tilde h}\mbox{$\mathfrak g$}mbda\tilde{h}^\mbox{$\mathfrak g$}mbda)={\rm p}si({}^{\tilde h}\mbox{$\mathfrak g$}mbda){\rm p}si(\tilde{h}^\mbox{$\mathfrak g$}mbda)=\cr& =&
{\rm p}hi_2({}^{\tilde h}\mbox{$\mathfrak g$}mbda){\rm p}hi_1({\rm p}hi_{\tilde{H}}(\tilde{h}^{\mbox{$\mathfrak g$}mbda}))\;.
{\rm e}nd{eqnarray}
So we can define the left $H$-action on ${J_{\mbox{\tiny H}}}^{-1}(\underline{e})$ by choosing any lift $\tilde h$ of $h{\rm i}n H$ and letting $$h[\tilde{g}_1,\gammamma_1,\gammamma_2,\tilde{g}_2]=a\{({\rm p}hi_{\tilde{H}}(\tilde{h}),\gammamma_2,{}^{\tilde{h}}\gammamma_2,{\rm p}hi_{\tilde{H}}(\tilde{h}^\gammamma_2))[\tilde{g}_1,\gammamma_1,\gammamma_2,\tilde{g}_2]\}=[{\rm p}hi_{\tilde{H}}(\tilde{h})\tilde{g}_1,\gammamma_1,{}^h\gammamma_2,{\rm p}hi_{\tilde{H}}(\tilde{h}^{\gammamma_2})\tilde{g}_2]\;.$$
The independence on the choice of the lift $\tilde{h}$ is clear since $(\tilde{h}z)^\gammamma=\tilde{h}^\gammamma z$ for any $z{\rm i}n Z_H$ due to point $ii$) in Lemma \ref{lift_dressing_univ_cover}.
Under this condition, the coisotropic reduction is obtained as a quotient of the free and proper action of $H$ and so it is a smooth manifold. Moreover, groupoid structures descend to the quotient, as it can be directly verified and everything goes through like in the proof of Theorem \ref{thm_groupoid}.
{\rm e}nd{proof}
In the following we analyze some obvious conditions that imply relative completeness.
{\rm tr}gin{lem}\mbox{$\mathfrak g$}bel{relative_completeness}
If $H^{\rm p}erp$ is simply connected and $H$ is a Poisson-Lie subgroup, then $(H,H^{\rm p}erp)$ are relatively complete.
{\rm e}nd{lem}
{\rm tr}gin{proof} Due to Lemma \ref{lem_h_hperp_inacca}, the dressing vector fields of $H^{\rm p}erp$ restricted to $H$ are zero and the action of $H^{\rm p}erp$ is trivially integrated. Since the hypothesis $ii$) of Lemma 4.1 in \cite{Mj} is obviously satisfied and $H^{\rm p}erp$ is simply connected, we get the result. {\rm e}nd{proof}
\subsection{An Example: $G=SU(1,1), H=U(1)$.}\mbox{$\mathfrak g$}bel{example_su11}
Let us consider the following double Lie algebra ${\mathfrak d}=s{\rm e}ll(2,{\mathbb C})$ with pairing $\mbox{$\mathfrak g$}ngle A,B\rangle={\rm Im\,Tr}(AB)$ and
$${\mathfrak g}=\mathfrak{su}(1,1)=\left\{\left({\rm tr}gin{array}{cc}ia & b\cr b^*&-ia {\rm e}nd{array}\right)\;, a{\rm i}n{\mathbb R}, b{\rm i}n{\mathbb C}\right\}~~,$$
$${\mathfrak g}^\star=\mathfrak{sb}(2,{\mathbb C})=\left\{\left({\rm tr}gin{array}{cc}a & n\cr0&-a {\rm e}nd{array}\right)\;, a{\rm i}n{\mathbb R}\;, n{\rm i}n{\mathbb C}\right\}\;.$$
Since the group
$$G=SU(1,1)=\left\{\left({\rm tr}gin{array}{cc} \mathit{a}lpha&{\rm tr}ta\cr {\rm tr}ta^*& \mathit{a}lpha^*{\rm e}nd{array}\right),\, |\mathit{a}lpha|^2-|{\rm tr}ta|^2=1 \right\}$$
is embedded in $D=SL(2,{\mathbb C})$, formulas (\ref{poisson_tensors}) define a multiplicative Poisson structure on $SU(1,1)$, even if it is not simply connected. The simply connected dual group is
$$G^*=SB(2,{\mathbb C})=\left\{\left({\rm tr}gin{array}{cc} A&N\cr 0& A^{-1}{\rm e}nd{array}\right),\, A>0, N{\rm i}n{\mathbb C}\right\}\;.$$
Let us choose as subgroup $H\subset G$ the diagonal $U(1)$, which
is a Poisson-Lie subgroup; then $H^{\rm p}erp$ is the closed subgroup
of $G^*$ of strictly upper diagonal matrices
$$
H^{\rm p}erp = \left\{ \left({\rm tr}gin{array}{cc}1 & N\cr 0&1{\rm e}nd{array}\right)\, ,\, N{\rm i}n {\mathbb C}\right\}~~~~.
$$
The quotient
$U(1)\backslash SU(1,1)$ is homeomorphic to the open disk and its quantization has been studied in \cite{Kor}.
Dressing transformations are not complete. An easy way of looking at it is the following. Let $g{\rm i}n SU(1,1)$ and $\xi{\rm i}n\mathfrak{g}^\star$: the flux $g_t$ of the dressing vector field corresponding to $\xi$ is given locally by the solution of $g{\rm e}xp t\xi=\gammamma_t g_t$ with $\gammamma_t{\rm i}n G^*$. We see that for $t{\rm i}n{\mathbb R}$ the equation
$$
\left( {\rm tr}gin{array}{cc}\mathit{a}lpha&{\rm tr}ta\cr{\rm tr}ta^*&\mathit{a}lpha^*{\rm e}nd{array}\right)\left({\rm tr}gin{array}{cc}1&t\cr0&1{\rm e}nd{array}\right)=\left({\rm tr}gin{array}{cc}A_t&N_t\cr0&A_t^{-1}{\rm e}nd{array}\right)
\left({\rm tr}gin{array}{cc}\sigma_t & \tau_t\cr\tau_t^*&\sigma_t^* {\rm e}nd{array}\right)~~~$$
admits in general solutions only for $t<t_0$ (for instance take $\mathit{a}lpha,{\rm tr}ta{\rm i}n{\mathbb R}$ with ${\rm tr}ta\not=0$). In particular the dressing action of $H^{\rm p}erp$ on $G$ is not complete. On the contrary, one easily computes that
$$
\left( {\rm tr}gin{array}{cc}\mathit{a}lpha&0\cr0&\mathit{a}lpha^*{\rm e}nd{array}\right)\left({\rm tr}gin{array}{cc}1&b\cr0&1{\rm e}nd{array}\right)=\left({\rm tr}gin{array}{cc}1&\mathit{a}lpha^2 b\cr0&1{\rm e}nd{array}\right)
\left({\rm tr}gin{array}{cc}\mathit{a}lpha & 0\cr 0& \mathit{a}lpha^* {\rm e}nd{array}\right)~~~,$$
so that $(H,H^{\rm p}erp)$ are relatively complete. Then Theorem \ref{thm_groupoid_general} produces a symplectic groupoid for the quotient Poisson structure on the disc. A subfamily of the whole family of covariant Poisson discs given in \cite{Kles} can be described in a similar manner.
\subsection{Comparison with the construction in \cite{Lu2007}} In \cite{Lu2007} the most general Poisson homogeneous spaces of Poisson Lie groups are considered. Drinfeld in \cite{Dr} showed that Poisson structures on $H\backslash G$, such that the right $G$ action is Poisson, are naturally associated to lagrangian subalgebras ${\mathfrak l}\subset{\mathfrak d}$. The case of $H$ coisotropic, considered in this paper, corresponds to ${\mathfrak l}={\mathfrak h}\mbox{$\Omega^{1}(P)$}lus {\mathfrak h}^{\rm p}erp$.
Let us assume that $i$) $G$ is a closed subgroup of any $D$ integrating $\mathfrak d$ (even not simply connected); $ii$) $H=L_H\cap G$, where $L_H$ is the connected subgroup of $D$ integrating $\mathfrak l$; $iii$) the infinitesimal action of $\mathfrak l$ on $G$ is integrated to a finite action of $L_H$. Then a Poisson groupoid for any
Poisson homogeneous space, even non embeddable, is constructed. Moreover
conditions for the Poisson structure to be non degenerate are
given.
If we restrict to the embeddable homogeneous spaces, that we consider in the present paper, and to the complete case, the
groupoid is described as $G\times_H H^{\rm p}erp$, the fibred product with respect to the right $H$-action on $G\times H^{\rm p}erp$ given by
$(g,\gammamma)h=(gh,{}^{h^{-1}}\gammamma)$. In this case the Poisson structure is non degenerate. We can describe our symplectic
groupoid ${\cal G}(H\backslash G)$ as a fibred product $H^{\rm p}erp\times_H G$ with respect to the left action $h(\gammamma,g)=({}^h\gammamma,hg)$,
via the correspondence $(\underline{g}\gammamma){\rm i}n{J_{\mbox{\tiny H}}}^{-1}(\underline{e})\rightarrow [{}^g\gammamma,g]{\rm i}n H^{\rm p}erp\times_H G$. It is then clear that the reduction procedure in \cite{Lu2007} coincides with the right version of our procedure.
In the non complete case the two constructions are different. The groupoid in \cite{Lu2007} is described as ${\cal G}amma=G\times_H
L_H/H$, where $L_H\subset D$ is the connected subgroup integrating ${\mathfrak l}={\mathfrak h}\mbox{$\Omega^{1}(P)$}lus {\mathfrak
h}^{\rm p}erp\subset\mathfrak{d}$ and $L_H/H$ is the homogeneous space by right quotient of $H\subset L_H$. The hypothesis that the action of $\mathfrak{l}$ on $G$ can be integrated implies that the dressing vector fields
corresponding to $\mathfrak{h}^{\rm p}erp$ are complete on $G$. The Poisson structure is not known to be symplectic in general.
In order to realize that this construction is, in general, different from ours, it is enough to look at the trivial case, where
$H=\{e\}$ and $H^{\rm p}erp=G^*$. This case obviously satisfies the relative completeness requirement: the symplectic groupoid
described in Theorem \ref{thm_groupoid_general} is obviously the unreduced one ${\cal G}(G)$. The construction in \cite{Lu2007} gives
${\cal G}amma=G\times G^*$, which is not a groupoid. In fact, the requirement that the action of $\mathfrak{l}={\mathfrak g}^*$
integrates is equivalent to completeness.
A less trivial case is given by the example discussed in subsection \ref{example_su11}. In that case, $L_H= H\bowtie H^{\rm p}erp$. We saw in
fact that the infinitesimal dressing action of $H^{\rm p}erp$ is complete only when restricted to $H$,
where it is trivial, and is not complete on the whole $SU(1,1)$.
\section{Concluding remarks}
In the complete case, the symplectic groupoid ${\cal G}(H\backslash G)$ described in the previous section has the source fibre isomorphic to $H^{\rm p}erp$, so it will be the unique source simply connected groupoid integrating $H\backslash G$ only if $H^{\rm p}erp$ is simply connected. Moreover, since we are interested in the problem of quantization a more explicit description will be necessary. In particular it is natural to ask when it is symplectomorphic to $T^*(H\backslash G)$ with the canonical symplectic form. This problem will be addressed elsewhere, while in this section we will sketch a construction of a diffeomorphism between the symplectic groupoid and the cotangent bundle, that can be considered a first step in this direction.
In the complete case, the symplectic groupoid ${\cal G}(H\backslash G)$ can be described as the fibre bundle $H^{\rm p}erp \times_H G$,
associated with the principal bundle $G\rightarrow H\backslash G$ and the dressing action of $H$ on $H^{\rm p}erp$. Since the cotangent
bundle is the bundle associated to the coadjoint action on $\mathfrak{h}^{\rm p}erp$, let us suppose that there exists a
diffeomorphism $s_H:{\mathfrak h}^{\rm p}erp\rightarrow H^{\rm p}erp$ that intertwines the coadjoint action of $H$ with the dressing action,
{{\rm i}t i.e.} $s_H({\rm Ad}^*_h\xi)={}^hs_H(\xi)$, for any $h{\rm i}n H$, $\xi{\rm i}n{\mathfrak h}^{\rm p}erp$. We then have a fibre bundle
isomorphism that we describe as follows. Let us consider any trivialization of the principal bundle $G\rightarrow H\backslash
G$ given by the local sections $g_i:U_i\rightarrow G$ and transition functions $h_{ij}: U_i\cap U_j\rightarrow H$, such that
$g_j(x)=h_{ji}(x)g_i(x)$ for any $x{\rm i}n U_i\cap U_j$. Then there exist local diffeomorphisms $S_i: {\cal G}|_{U_i} \rightarrow T^*
H\backslash G|_{U_i}$ given by:
{\rm tr}gin{equation}
S_i(x \gamma)= {\rm Ad}^*_{g_i(x)^{-1}}(s_H^{-1}({}^{g_i(x)} \gamma)) {\rm i}n {\rm Ad}^*_{g_i(x)^{-1}}{\mathfrak h}^{\rm p}erp=T^*_x(H\backslash G) \;.\nonumber
{\rm e}nd{equation}
Since $s_H$ intertwines coadjoint and dressing action of $H$, $S_i=S_j$ on $U_i\cap U_j$ so that a global diffeomorphism $S:{\cal G}(H\backslash G)\rightarrow T^*(H\backslash G)$ is defined. Since the source map, when transported to the cotangent bundle, coincides with the bundle projection, the symplectic structure cannot be the canonical one, unless the Poisson structure on $H\backslash G$ is trivial.
Let us briefly see a class of examples where to apply the above construction. When $H$ is a Poisson Lie group and $H^{\rm p}erp$ is of exponential type, {{\rm i}t i.e.} $H^{\rm p}erp={\rm e}xp{\mathfrak h}^{\rm p}erp$, we can choose $s_H={\rm e}xp$. In fact, since $\mathfrak{h}^{\rm p}erp$ in an ideal, the coadjoint action of $H$ on $H^{\rm p}erp$ is a Lie algebra morphism: $Ad_X^* \left( [\xi, {\rm e}ta] \right) = [Ad_X^*\xi, {\rm e}ta] + [\xi,Ad_X^* {\rm e}ta]$, for all $X {\rm i}n \mbox{${\mathfrak h}$}, \xi,{\rm e}ta {\rm i}n \mbox{${\mathfrak h}$}^{\rm p}erp$. Then due to the uniqueness of the group automorphism that integrates the coadjoint action we conclude that ${}^h{\rm e}xp\xi={\rm e}xp{\rm Ad}^*_h\xi$.
While we we were finishing this paper, it appeared on the net paper \cite{stefanini} that contains very close results. It is shown that the Poisson action of a complete Poisson Lie group $H$ on an integrable Poisson manifold $P$ can be lifted to a groupoid action of ${\cal G}(H^*)$ on ${\cal G}(P)$; this fact allows one to obtain the groupoid integrating $P/H$ by symplectic reduction. The result coincides with Theorem \ref{thm_groupoid} in our paper when we take $P=G$ as a Poisson Lie group and $H\subset G$ a Poisson Lie subgroup. It would be nice to extend the results of \cite{stefanini} to the most general coisotropic reduction described in Theorem \ref{thm_poi_red} in order to get our Theorem \ref{thm_groupoid} in full generality as a particular case of this reduction scheme.
{\rm tr}gin{thebibliography}{666666}
\bibitem{BCZ} F. Bonechi, A. S. Cattaneo and M. Zabzine: Geometric quantization and non-perturbative Poisson sigma model. Adv.Theor.Math.Phys.10:683-712, (2006).
\bibitem{CaFe} A. Cattaneo and G. Felder: Poisson sigma model and symplectic groupoid. In {{\rm i}t Quantization of singular symplectic quotients}, vol.198 of Progr.Math., 61-93, Birkhauser, Basel (2001).
\bibitem{CL} A. Connes and G. Landi: Noncommutative Manifolds the Instanton Algebra and Isospectral Deformations. Commun.Math.Phys. 221 (2001) 141-159.
\bibitem{CDV} A. Connes, M. Dubois-Violette: Noncommutative finite-dimensional manifolds. I. Spherical manifolds and related examples. Commun. Math. Phys. {\bf 230} (2001), 539-579.
\bibitem{CrFe} M. Crainic and R. L. Fernandes: Integrability of Lie brackets. Ann.of Math. 2 {\bf 157(2)} (2003), 575-620.
\bibitem{Dr} V. G. Drinfel'd: On Poisson homogeneous spaces of Poisson-Lie groups. Theo. Math. Phys. {\bf 95} 2 (1993), 226-227.
\bibitem{FOR} R. L. Fernandes, J. P. Ortega, T. S. Ratiu: The momentum map in Poisson geometry. [arXiv:0705.0562].
\bibitem{H} E. Hawkins: A Groupoid Approach to Quantization. [arXiv:math/0612363].
\bibitem{Ka} M. V. Karasev: Analogues of objects of the theory of Lie groups for nonlinear Poisson brackets. Izv. Akad. Nauk SSSR Ser. Mat., {\bf 50}, 638, (1986), 508-538. English translation: Math. USSR-Izv. {\bf 28} 3 (1987), 497-527.
\bibitem{Kles} S. Klimek and A. Le\'sniewski: Quantum Riemann Surfaces I. The Unit Disc. Comm. Math. Phys. {\bf 146}, 103--122 (1993).
\bibitem{Kor} L.I. Korogodsky: Quantum Group $SU(1,1)\times \mathbb Z_2$ and "Super-Tensor" Products, Comm.Math.Phys. {\bf 163} (1994), 433-460.
\bibitem{LuTh} J.-H. Lu: ``{{\rm e}m Multiplicative and affine Poisson structures on Lie groups}''. Phd thesis, Univ. of California, Berkeley, (1990).
\bibitem{Lu2007} J.-H. Lu: A note on Poisson homogeneous spaces. [arXiv:0706.1337].
\bibitem{LW} J.-H Lu and A. Weinstein: Groupoides symplectiques doubles des groupes de Lie-Poisson. C.R.Acad.Sc.Paris, {\bf 309} (1989), 951-954.
\bibitem{LW2} J.-H Lu and A. Weinstein: Poisson Lie groups, dressing transformations and Bruhat decompositions. J.Differential Geometry {\bf 31} (1990) 501-526.
\bibitem{MK} K.C.H. Mackenzie, {{\rm i}t General theory of Lie groupoids and Lie algebroids}. Cambridge University Press, (2005).
\bibitem{Mj} S. Majid: Matched pairs of Lie groups associated to solutions of the Yang-Baxter equations. Pac.J.of Math. {\bf 141} 2, (1990), 311-332.
\bibitem{MW} K. Mikami and A. Weinstein: Moments and Reduction for Symplectic Groupoids. Publ. RIMS. Kyoto Univ. {\bf 24} (1988), 121-140.
\bibitem{Rieffel} M. Rieffel, Deformation quantization for actions of
$\mathbb R^d$, Mem. Amer. Math. Soc. {\bf 106} (1993).
\bibitem{STT} M. A. Semenov-Tian-Shansky: Dressing transformations and Poisson Lie group actions. Publ. RIMS, Kyoto Univ. {\bf 21} (1985), 1237-1260.
\bibitem{stefanini} L. Stefanini: Integrability and reduction of Poisson group actions. arXiv:0710.57532 [math.SG].
\bibitem{We1987} A. Weinstein: Symplectic groupoids and Poisson manifolds. Bull. Amer. Math. Soc.(N.S.) {\bf 16} (1987), 101-104.
\bibitem{We1} A. Weinstein: Coisotropic calculus on Poisson manifolds. J. Math. Soc. Japan {\bf 40} (4) (1988), 705-726.
\bibitem{We2} A. Weinstein: Symplectic groupoids, geometric
quantization and irrational rotation algebras, in {{\rm i}t Symplectic
geometry, groupoids and integrable systems}. Springer NY (1991),
281-290.
\bibitem{WX} A. Weinstein, P. Xu: Classical solutions of the quantum Yang-Baxter equations. Commun.Math.Phys. {\bf 148} (1992) 309-343.
\bibitem{Xu} P. Xu: Symplectic groupoids of reduced Poisson spaces. C.R.Acad.Sci.Paris Serie I {\bf 314} (1992), 457-461.
\bibitem{Xu1} P. Xu: Poisson manifolds associated with group actions and classical triangular $r$--matrices. J. Funct. Anal. {\bf 112} (1993), 218-240.
\bibitem{Xu2} P. Xu: Dirac submanifolds and Poisson involutions.
Ann. Sci. Ecole Norm. Sup. (3) {\bf 36 } (2003), 403-430.
\bibitem{XW} P. Xu and A. Weinstein: Extension of symplectic groupoids and quantization. J. Reine Angew. Math. {\bf 417} (1991), 159-189.
{\rm e}nd{thebibliography}
{\rm e}nd{document} | math |
Was Your Umbilical Cord Knotted?
The umbilical cord has been described as the baby’s lifeline. It develops from the placenta and is responsible for providing important nutrients to the baby. Disruptions in the transfer of blood and oxygen through the umbilical cord can lead to serious injuries in a baby.
As a baby moves around in the mother’s womb, the umbilical cord can become knotted. If this happens, then there is a threat for a reduced level of blood and oxygen in the baby. When a baby’s oxygen level gets too low, then fetal hypoxia can occur. Hypoxic ischemic encephalopathy, which is a reduced level of blood and oxygen, leading to a brain injury, can be the result of a knotted umbilical cord. A subsequent cerebral palsy diagnosis can also be the result of a brain injury.
When a mother presents with certain types of risk factors, doctors can test prenatally for the presence of true knots in the umbilical cord. Doctors can use ultrasounds to detect the presence of a knotted umbilical cord. If a doctor fails to order certain tests to detect true knots, and the baby suffers a birth injury because of the failure to perform the tests, a strong argument will be made that the doctor fell below the standard of care, causing the baby’s injury, especially if mother presents with the risk factors which should alert the doctor to test.
What Are Some Of The Risk Factors For A Knotted Umbilical Cord?
Hypoxic ischemic encephalopathy is essentially defined as a reduced level of blood and oxygen, resulting in a brain injury. For babies who experience a knotted umbilical cord, or a true knot in the umbilical cord, doctors must pay close attention due to what can be at stake if the baby suffers a reduction of blood and oxygen.
In some cases of a knotted cord, the knot is not tight enough to impede the flow of blood and oxygen. However, a knot that starts off not restricting the flow of oxygen can later develop into a knot that in fact does restrict blood and oxygen. This is because as the child develops, he or she begins to move more and more. Flip and spinning movements can lead to a once “loose” knot, tightening. It is at this point that a reduction in blood and oxygen can present itself. Therefore, doctors must take ample precautions when a knotted umbilical cord is detected.
A mother might notice decreased movement in her baby. As the baby grows, they may slip through a loop in the umbilical cord. After 37 weeks, if there is decreased activity in the baby, a knotted umbilical cord might be the culprit.
Doctors can use an ultrasound to diagnose a knotted umbilical cord. Fetal tracings may also suggest the presence of a knot through sudden drops in the fetal heart rate. With that said, the ultrasound can be the best way to confirm or rule out the presence of a knot. Certain risk factors should alert doctors to perform testing to see if the umbilical cord is knotted. Even though many knots form later in the pregnancy, in general, a knot can form at any time.
Decreased fetal movement, the presence of a long umbilical cord, and a male baby can be some of the things which strongly suggest that a knot could be in the cord and that an ultrasound is needed to confirm or rule out the diagnosis. Add to this, when mother is carrying multiple babies, the chances of a knotted umbilical cord increases. Doctors must be aware of these factors, and others, especially when mother is reporting a sudden decrease in movement of the baby.
If fetal hypoxia is suspected due to a knotted umbilical cord, doctors will need to move to a C-Section. Therefore, close monitoring is required for this medical condition. A loose knot can tighten at any time, which can increase the chances of the baby suffering a brain injury.
Did A Knotted Umbilical Cord Cause A Brain Injury In Your Baby?
Certain factors require that doctors must test for a knotted umbilical cord. If doctors fail to identify these factors, and not test, fetal hypoxia, or death can be the result. Mothers who express concern over decreased baby movement will generally explain these concerns to their doctor and look to their doctor for guidance. A strong argument for medical malpractice can be made if doctors fail to act appropriately regarding certain risk factors regarding a knotted umbilical cord and injury occurs.
Did your baby's umbilical cord have knots in it and now your child has a birth injury? | english |
बाय इंडियन पब्लिक मेल , २७ अक्टोबर, २०१८, १६:३०
पेरिस, फ्रेंच ओपन बैडमिंटन टूर्नामेंट के क्वार्टर फाइनल मुकाबले में भारत की साइना नेहवाल को हार का सामना करना पड़ा। विश्व की नंबर वन खिलाड़ी ताइ जु यिंग ने साइना नेहवाल को २०-२२ और ११-२१ से हराकर टूर्नामेंट से बाहर कर दिया। साइना ने पहले गेम में अच्छा खेल दिखाया लेकिन इसके बाद वह चीनी ताइपै की खिलाड़ी के सामने नहीं टिक पाई और २०-२२, ११-२१ से हार गई। यह साइना की ताइ-जु के हाथों लगातार १२वीं हार है।
वहीं इससे पहले पीवी सिंधू ने जापान की सायाका सातो को सीधे गेम में हराकर क्वार्टर फाइनल में जगह बनाई लेकिन बी साइ प्रणीत हारकर बाहर हो गए। तीसरी वरीयता प्राप्त सिंधू ने सायाका को २१-१७ और २१-१६ से हराया। अब सिंधू का सामना सातवीं वरीयता प्राप्त हि बिंगजियाओ से होगा। दूसरी ओर प्रणीत को इंडोनेशिया के जोनाथन क्रिस्टी ने २१-१६ और २१-१४ से हराया।
पुरूष युगल में सात्विक साइराज रांकीरेड्डी और चिराग शेट्टी तथा मनु अत्री और बी सुमित रेड्डी की जोड़ियों ने भी अंतिम आठ में जगह बना ली। सात्विक और चिराग ने चीन के हि जितिंग और तान कियांग को २१-१३ और २१-१९ से हराया जबकि मनु और सुमित ने चीन के लियू चेंग और झांग नान की तीसरी वरीयता प्राप्त जोड़ी को २१-१४ और २१-१६ से शिकस्त दी। मेघना जे और पूर्विषा एस राम को चौथी वरीयता प्राप्त इंडोनेशिया की ग्रेसिया पोली और अप्रियानी राहायु ने २१-१५ और २१-१३ से हराया। | hindi |
بادشاہن تہٕ وزٟرَن ییٚلہِ تَس سٟتۍ خٲر پٲٹھ کوٚر تہٕ تِمَو پرٛزٕ نووُے نہٕ سُہ | kashmiri |
Second time’s a charm, right? Ryan O’Callaghan, the former professional NFL football player for the New England Patriots and Kansas City Chiefs, has come out… for the second time.
O’Callaghan previously implied he was gay when he mentioned having a boyfriend in 2014; however, no one really noticed his big announcement. | english |
In-Ear earbuds with team logo 3D printed design, official MLB logo wire slider, and team insignia on the head jack.
This entry was posted on March 23, 2012 at 3:48 pm and is filed under Arizona Diamondbacks. You can follow any responses to this entry through the RSS 2.0 feed. | english |
होम | आध्यात्मिकता | आप जीनियस हैं या सीज़ोफ्रीनिक? दीजिए इन ३ सवालों के जवाब और जानिए
आपको जानकर आश्चर्य होगा कि हमारा मस्तिष्क ९८ प्रतिशत काम अचेत अवस्था में करता है। आपका दिमाग कितना तेज है और कितना बीमार यह आप एक साधारण से टेस्ट से पता कर सकते हैं।माइंड टेस्ट गेमी इन हिन्दी :- नीचे हम आपसे कुछ साधारण से सवाल पूछ रहे हैं, जिनके जवाब आपको यह बताएंगे कि
यह आलेख निम्नलिखित के बारे में जानकारी प्रदान करता है : बीमार एंड मस्तिष्क
आपको जानकर आश्चर्य होगा कि हमारा मस्तिष्क ९८ प्रतिशत काम अचेत अवस्था में करता है। आपका दिमाग कितना तेज है और कितना बीमार यह आप एक साधारण से टेस्ट से पता कर सकते हैं।
नीचे हम आपसे कुछ साधारण से सवाल पूछ रहे हैं, जिनके जवाब आपको यह बताएंगे कि आपका दिमाग कितना तेज है। सवाल पढ़िए और जवाब दीजिए, लेकिन इसे हल्के में मत लीजिए क्योंकि इनके जवाब देना हर किसी के बस की बात नहीं। जिसने भी इसका सही जवाब दिया, वह या तो जीनियस है या सीज़ोफ्रीनिक।
सवाल १: एक रेस कार और चक्रवात में क्या समानता है?
{ पढ़ें :- मन की ज़्यादा न सुनें, अन्तरात्मा की आवाज़ सुनना है हितकर }
सवाल २: केतली और भाप इंजन में क्या समानता है?
सवाल ३: एक पेंसिल और जूते में क्या समानता है?
आपका जवाब आपके बारे में क्या कहता है, जानने के लिए देखिए वीडियो। सही जवाब जानने के लिए नीचे देखें। | hindi |
In this thread you can find all news articles concerning Tomb Raider II: Starring Lara Croft.
Since October 28 the mobile version of Tomb Raider II is also available in the Google Play Store (for Android Smart Phones and Tablets). The iOS version has been around since December 2014 and now finally Android users can enjoy the overhauled game as well.
The game features better graphics (with new textures) and Achievements. The game, which is available for 99 cents in the European store, includes the add on levels for "The Golden Mask". Change to the add on by clicking on the icon with the four squares.
Just like with part 1 the controls take some getting used to, but the game still promises a lot of fun, especially when you try locking Winston in the freezer for an achievement. Please note that the game can prove a little annoying here: when you've started the Manor from the Golden Mask menu, manor-specific achievements might not pop, so make sure you switch back to Tomb Raider II before paying the manor a visit.
More screenshots can be found in our galleries. | english |
Warmth and heating have always been crucial in the species development (even for the cold-blooded species!). Mammals need heat to survive and this basic concept is applied in all homes and interiors where the climate is a problematic issue. In most of the houses there are heaters from a central heating (bio, geothermic, methane-based, solar...) that allow to overcome the bad season. Shapes and forms have evolved from mere heating tools that needed to be hidden behind curtains or grids to super-designy pieces that claim - and deserve - a central space in the living rooms and around the house. | english |
\begin{document}
\title{ itleName}
\pagestyle{plain}
\begin{abstract}
Distributed quantum computing (DQC) is a promising approach to extending the computational power of near-term quantum devices.
However, the non-local quantum communication between quantum devices is much more expensive and error-prone than
the local quantum communication within each quantum device.
Previous work on the DQC communication optimization focus on optimizing the communication protocol for each individual non-local gate and then adopt quantum compilation designs which are designed for local multi-qubit gates (such as controlled-x or CX gates) in a single quantum computer.
The communication patterns in distributed quantum programs are not yet well studied, leading to a far-from-optimal communication cost.
In this paper, we identify \textit{burst communication}, a specific qubit-node communication pattern that widely exists in many distributed programs and can be leveraged to guide communication overhead optimization.
We then propose \frameworkName, an automatic compiler framework to first extract the burst communication patterns from the input programs, and then optimize the communication steps of burst communication discovered.
Experimental results show that our proposed AutoComm can reduce the communication resource consumption and the program latency by 75.6\% and 71.4\% on average, respectively.
\end{abstract}
\section{Introduction}
Quantum computing is promising with its great potential of providing significant speedup to many problems, such as large-number factorization with an exponential speedup \cite{Shor} and unordered database search with a quadratic speedup \cite{Grover}.
A large number of qubits is required in order to solve practical problems with quantum advantage and the qubit count requirement is even higher after taking quantum error correction \cite{nielsen2002quantum} into consideration.
However, it has turned out that extending the number of qubits on a single quantum processor is exceedingly difficult due to various hardware-level challenges such as crosstalk errors \cite{crosstalk1,crosstalk2}, qubit addressability~\cite{bruzewicz2019trapped}, fabrication difficulty~\cite{brink2018device}, etc.
The challenges usually increase with the size of quantum hardware and may limit the number of qubits accommodated by a single quantum processor.
Rather than relying on the advancement of a single quantum processor, an alternative way of increasing scalability is by distributed quantum computing (DQC), which integrates the computing resources of multiple modular quantum processors.
For example, recent experiments have demonstrated an entanglement-based quantum network of three quantum processors \cite{QNexp_3-node_network}. Companies such as IBM also envision in their roadmap \cite{IBM2020roadmap} a
future of creating a large-scale quantum computer
with quantum interconnects that link superconducting quantum processors.
Similarly, the ion trap-based quantum computer also
requires an optical network of multiple traps each with tens of qubits in-order to scale up, making DQC a path to realizing large-scale quantum computers \cite{monroe2012}.
In DQC, remote communication involving qubits in different computing nodes is essential yet far more expensive than the local communication on qubits within the same node (e.g., 5-100x time consumption and up to 40x accuracy degradation~\cite{time-slice, Young2022AnAF}).
There are two major schemes for remote quantum communication: one built upon the cat-entangler and cat-disentangler protocol~\cite{cat_entangle}, and the other based on the quantum teleportation~\cite{nielsen2002quantum}.
In this paper, we denote the former scheme as Cat-Comm and the latter one as TP-Comm.
Both schemes consume EPR pairs~\cite{optimal_nonlocal}, which are pre-distributed entangled qubit pairs, as a resource to establish quantum communication.
Cat-Comm can implement the remote CX gate~\cite{nielsen2002quantum} with only one EPR pair, but for general two-qubit gates like the SWAP gate~\cite{nielsen2002quantum}, Cat-Comm requires up to three EPR pairs~\cite{Ferrari2021CompilerDF}. In contrast, TP-Comm conducts any remote two-qubit gate with two EPR pairs~\cite{optimal_nonlocal}, making it more efficient for the SWAP gate. For a distributed program, more complex remote operations or more information getting transferred per EPR pair would lead to less communication cost.
The overall compiling flow for DQC is similar to that of single-node quantum programs, except with more emphasis on remote communication overhead.
Ferrari et al.~\cite{Ferrari2021CompilerDF} propose a compiler design similar to single-node compilers~~\cite{Li2019TacklingTQ, Qiskit, Amy2019staqAFQ, Khammassi2022OpenQLA, Sivarajah2020tketAR} using Cat-Comm for each remote CX gate and TP-Comm for each remote SWAP gate. Unsatisfied with the low information of the remote CX gate, Baker et al.~\cite{time-slice} eliminate all remote CX gates by using the remote SWAP gate, which only requires two EPR pairs for implementation but contains the information of three CX gates. Unfortunately, bounded by the information of a single two-qubit gate, these compilers cannot achieve higher throughput of information per EPR pair.
Eisert et al.~\cite{optimal_nonlocal} suggest higher throughput could be achieved by considering multi-qubit gates. Diadamo et al.~\cite{Diadamo2021DistributedQC} propose a specialized compiler for distributed VQE that uses Cat-Comm to implement controlled-unitary-unitary and controlled-controlled-unitary gates. However, their work can only optimize the gate written in the controlled-unitary form and thus cannot work with decomposed circuits. Moreover, their work
cannot optimize programs lacking controlled-unitary blocks.
Besides increasing the `height' (number of qubits) of remote operations, we observe that the throughput of information per EPR pair can also be significantly boosted up by expanding the `width' (number of gates) of each remote communication. Specifically, we discover that a large amount of remote two-qubit gates in distributed quantum programs can be implemented collectively through one or two communication invocations. On top of the observation, we propose to optimize the communication overhead based on the \textit{burst communication}, which denotes a group of continuous remote two-qubit gates between one qubit and one node. Burst communication is powerful as it is more information-intensive than single two-qubit gate and contains but not limited to controlled-unitary blocks. Burst communication is also flexible for optimization as it does not require specialized circuit representation and is available in decomposed circuits.
\begin{figure}
\caption{AutoComm Overview.}
\label{fig:designoverview}
\end{figure}
To this end, we develop the first burst-communication-centric optimization framework, \textit{\frameworkName} as shown in Figure~\ref{fig:designoverview}.
In contrast to existing compiling flows~\cite{time-slice, Ferrari2021CompilerDF, Li2019TacklingTQ, Qiskit, Amy2019staqAFQ, Khammassi2022OpenQLA, Sivarajah2020tketAR}, where each remote CX gate is implemented independently (i.e., sparse communication), \textit{\frameworkName} greatly mitigates the communication bottleneck with burst communication and can be easily integrated into these existing compiling flows.
Our framework consists of three key stages. Firstly, we perform a communication aggregation pass to group remote gates and extract burst communication blocks.
Due to the broad availability of burst communication in distributed quantum programs, this pass could generate a large amount of burst communication blocks for following optimizations.
Secondly, we propose a hybrid communication scheme which examines the patterns of each burst communication block and assigns the optimal communication scheme for each block. The insight for this step is that, TP-Comm and Cat-Comm is more resource-efficient for different type of burst communications and considering only one communication scheme would incur extra resource consumption.
Finally, we propose an adaptive communication schedule for burst communication blocks of different patterns to squeeze out the parallelism between them and thus reduce overall program latency.
There are two critical observations for this optimization: it is possible to execute burst communication with shared qubits or nodes in parallel, and we can fuse some burst communication blocks to cut down the communication footprint.
Our contributions are summarized as follows:
\begin{itemize}
\item We identify the burst communication feature in distributed quantum computing and promote its importance in optimizing distributed quantum programs. We further propose the first communication optimization framework based on the burst communication.
\item We propose a communication aggregation pass to expose burst communications of distributed quantum programs and then design a hybrid communication scheme, using both Cat-Comm and TP-Comm to accommodate different communication patterns.
\item We propose an efficient communication scheduling method to optimize the latency adaptively squeezing out the parallelism of various patterns.
\item Compared to the state-of-the-art baseline method~\cite{Ferrari2021CompilerDF}, AutoComm significantly reduces the communication resource consumption and the program latency by 75.6\% and 71.4\% on average, respectively.
\end{itemize}
\section{Background} \label{sect: bg}
In this section, we introduce necessary background to understand the distributed quantum computing and its communication.
We do not cover the basic quantum computing concepts (e.g., qubit, gate, measurement) and recommend ~\cite{nielsen2002quantum} for more details.
\subsection{EPR Pair and Entanglement}
\paragraph{EPR entanglement} To establish quantum communication in a distributed quantum computer, we first need to generate a pair of qubits whose state is $\frac{1}{\sqrt{2}}(\ket{00} + \ket{11})$, EPR entangled state.
The two qubits such state is called EPR entanglement pair (Abbrev., EPR pair)~\cite{nielsen2002quantum}.
The two qubits of an EPR pair can be distributed on different quantum devices, formulating a remote EPR pair~\cite{optimal_nonlocal}.
The preparation of the remote EPR pair includes two stages: generation and purification. The generation stage generates and distributes EPR pairs but is very noisy, making the purification stage indispensable~\cite{isailovic2006interconnection}.
\subsection{Distributed Quantum Computing}
The development of quantum communication~\cite{QNexp9, QNexp10, QNexp11, QNexp12, QNexp13, QNexp14, QNexp15, QNexp16, QNexp17, QNexp18, QNexp19, QNexp_3-node_network} enables distributed computing over a series of quantum devices. As in classical distributed computing, remote communication between computing nodes is also the bottleneck of distributed quantum computing (DQC) and should be carefully optimized.
Different from the classical distributed computing system, quantum data cannot be easily shared across quantum nodes due to the no-cloning theorem~\cite{nielsen2002quantum}.
The workaround is to exploit different communication schemes (e.g., \textit{Cat-Comm}~\cite{optimal_nonlocal} and \textit{TP-Comm}~\cite{nielsen2002quantum}) based on remote EPR entanglement, one of the key information resources in quantum processing.
Figure~\ref{fig:qucomm} illustrates how to use these two schemes to implement one \textit{remote CX gate}, with the control qubit $q_1$ residing in quantum nodes A and the target qubit $q_1'$ in node B. Qubits in Figure~\ref{fig:qucomm} fall into two categories. The first category of qubits is used to store quantum information and is called \textit{data qubits}, e.g., $q_1$ and $q_1'$. The second category of qubits, called \textit{communication qubits}, is used to hold the remote EPR entanglement required for quantum communication, e.g. $q_0$ and $q_0'$ in Figure~\ref{fig:qucomm}.
As shown in Figure~\ref{fig:qucomm}(a), the first communication scheme Cat-Comm utilizes cat-entangler to transfer the state of the control qubit $q_1$ to node B, execute the target CX gate, and then use cat-disentangler to transfer the state back to node A. While TP-Comm, the second communication scheme in Figure~\ref{fig:qucomm}(b), employs quantum teleportation~\cite{nielsen2002quantum} to transfer the state of $q_1$, and then execute the target CX gate. Though Cat-Comm and TP-Comm both require one EPR pair and two bits of classical communication,
Cat-Comm is more widely-used than TP-Comm in DQC compilers~\cite{Ferrari2021CompilerDF, Diadamo2021DistributedQC}.
This is mainly due to the dirty side-effect of TP-Comm.
We would need another invocation of
TP-Comm
to release the occupation of the communication qubit (e.g., $q_0'$ in Figure~\ref{fig:qucomm}(b)), which would be later used for other quantum communications. As a result, two EPR pairs are actually required to implement a single remote CX gate by TP-Comm, with one pair for handling the dirty side-effect.
\begin{figure}
\caption{The implementation of one remote CX. (a) The Cat-Comm version. (b) The TP-Comm version. Each wavy line denotes an EPR pair between qubits, and each dashed line denotes one bit of classical communication. M denotes measurement.}
\label{fig:qucomm}
\end{figure}
\begin{figure}
\caption{The optimized implementation of the controlled-unitary block $C-U1-U2$. (a) The Cat-Comm version. (b) The TP-Comm version. }
\label{fig:qucomm-cu}
\end{figure}
In Figure~\ref{fig:qucomm}, we only show how to implement one individual CX gate. To implement complex remote interactions between quantum nodes, one simple strategy is to first decompose the remote interaction into several remote CX gates and implement each remote CX gate as in Figure~\ref{fig:qucomm}. However, this strategy may incur heavy communication costs.
Prior work~\cite{cat_entangle} spots a more efficient way to implement a controlled-unitary block between two quantum nodes. Figure~\ref{fig:qucomm-cu} provides the optimized implementation of the controlled-block $C-U1-U2$, where $U1$ and $U2$ are some unitary quantum operations. The implementation in Figure~\ref{fig:qucomm-cu} only requires one EPR pair, fewer than implementing each remote two-qubit gate independently.
Besides the controlled-unitary block, we discover that plenty of quantum communications in distributed quantum programs can be transformed into a group of remote interactions between one qubit and one quantum node. We name such a group of remote interactions \textit{burst communication}. Different from the single CX case, Cat-Comm and TP-Comm each has its own advantage for burst communication of various patterns.
Unfortunately, existing DQC compilers~\cite{ILP, time-slice} either do not take advantage of the burst communication or only consider the basic controlled-unitary case~\cite{Diadamo2021DistributedQC}.
In later sections, we would use \textit{one remote EPR pair} and \textit{one remote communication} interchangeably, because for either Cat-Comm or TP-Comm, one invocation just requires one remote EPR pair.
\section{Problem and Motivation}
In this section, we first introduce the communication problem in distributed quantum programs and then identify the optimization opportunities by considering burst communication.
For the rest of the discussions, we assume quantum communication can be established between any two quantum nodes, a typical assumption in data-center distributed computing~\cite{van2002distributed}. We also assume that each quantum node has only two communication qubits, which is realistic for near-term DQC~\cite{Ferrari2021CompilerDF}.
\begin{figure}
\caption{Program snippet extracted from quantum arithmetic circuits~\cite{revlib}
\label{fig:example}
\end{figure}
\subsection{Communication Problem}
The example distributed program in Figure~\ref{fig:example} is modified from quantum arithmetic circuits~\cite{revlib}.
This program contains many remote CX gates whose control qubit and target qubit reside in different quantum nodes, e.g., $CX\, q_1,q_3$. Remote CX gates are inevitable in DQC especially when the program's qubit number is substantially larger than each quantum node's. To make the distributed program executable, we should transfer
the states of qubits in remote CX gates to make them locally executable temporarily. The state transfer involves remote communication between quantum nodes, which can be accomplished by Cat-Comm or TP-Comm.
Due to the noisy nature of quantum communication,
remote operations are far more error-prone than local quantum gates. The long runtime of quantum communication would also lead to the decoherence of quantum states. As a result, to produce high fidelity outcome,
we hope the number of remote communication to be as small as possible, so is the latency induced.
As indicated in Section~\ref{sect: bg}, one remote CX gate requires at least one remote communication.
While there is little room for optimizing the communication cost of one remote CX gate, there is a large optimization space when considering burst communication, which involves a group of remote CX gates. For example, we can execute the first two CX gates on $q_1, q_3$ in Figure~\ref{fig:example} collectively, with only one communication by using the circuit in Figure~\ref{fig:qucomm-cu}(a). From the perspective of information theory, burst communication is more informative than the communication with only one remote CX.
The overall communication cost and latency would be considerably lowered if handling all remote CX gates in this burst manner.
Fortunately, as we see in the next section, burst communication is prevalent in diverse distributed quantum programs.
\subsection{Burst Communication in DQC}\label{sect:burstcomm}
Aside from the arithmetic program shown in Figure~\ref{fig:example}, we also see burst communication in a variety of quantum programs.
As examples,
we examine the burst communication of the Quantum Fourier Transform (QFT) program~\cite{nielsen2002quantum} and the Quantum Approximate Optimization Algorithm (QAOA)~\cite{Farhi2014AQA} by hand. These two represent different categories of quantum programs: QAOA is one of the most important applications in near-term quantum computing whereas QFT is the building block circuit of quantum algorithms.
We first give a formal definition of the burst communication in DQC. In this paper, we refer to a group of continuous remote two-qubit gates between one qubit $q$ and one node as \textit{burst communication}. For two remote two-qubit gates $g_1$ and $g_2$, the continuity of these two gates means there are no other remote gates between $g_1$ and $g_2$.
To characterize the burst communication of a distributed program $dprog$, for a remote gate $g$ in $dprog$, we define function $\epsilon(g)$ to be the largest burst communication block
that contains $g$. The gate order of $dprog$ may affect the burst communication block found. $\epsilon(g)$ is defined to be the largest over all functional-equivalent gate order of $dprog$.
We then define $len(\epsilon(g))$ to be the number of remote CX gates in $\epsilon(g)$ if compiled to the CX+U3 basis~\cite{Qiskit}.
Finally, we are ready to define the inverse-burst distribution as follows:
\begin{align}
P(x) = \dfrac{\vert\{ g \vert len(\epsilon(g)) < x\} \vert}{\# g}.
\end{align}
A lower $P(x)$ suggests more burst communication.
\begin{figure}
\caption{(a) QFT program with two nodes and two qubits per node. (b) The layout for the maximal $P_4$.
Parameters omitted for simplicity.
For demonstration, we do not combine $\text{CRZ}
\label{fig:qftexam}
\end{figure}
We begin by examining the QFT program using the aforementioned definition.
We assume the total qubit number is $n$, the quantum node number is $k$, and qubits are evenly distributed across all nodes, with $t = \frac{n}{k}$ qubits per node. Figure~\ref{fig:qftexam} shows the QFT program with $k=2$ and $t=2$. For the QFT program, as shown in Figure~\ref{fig:qftexam}, each $q_i$ is controlled by all qubits $q_j$ (through the CRZ gate) that satisfies $j > i$~\cite{nielsen2002quantum}. First, we have $P(2) = 0$
because each CRZ gate in QFT is compiled into two CX gates, as illustrated in Figure~\ref{fig:qftexam}(a). Now, we consider $P(4)$. For the $i$-th qubit satisfies $i \le n-k$, the number of $j$ s.t. $\epsilon(\text{CRZ}_{ji}) < 4$ is at most $\lfloor \frac{i-1}{t-1} \rfloor$ because for one node, if at least two of its qubits have subscripts $> i$,
this node would have at least two qubits being interacted by qubit $i$. Since CRZ gates are commutable with each other, we could form a communication block with at least 4 CX gates. On the other hand, if $i > n-k$, then the $i$-th qubit is at most interacted with $n-i$ qubits, thus the number of $j$ s.t. $\epsilon(\text{CRZ}_{ji}) < 4$ is at most $n-i$.
Therefore, we have
$$P(4) \le \frac{\sum_{i=1}^{n-k} \lfloor\frac{i-1}{t-1}\rfloor + \sum_{i=n-k+1}^n (n-k)}{\sum_{i=1}^n (n-i) - k\sum_{l=1}^t (t-l) } = \frac{1}{t}.$$
This indicates there are $1-P(4)=1-\frac{1}{t}$ remote gates within a communication block that possesses more than 4 CX gates. Generally, we can prove that $P(2m) \le \frac{m-1}{t}$. This upper bound is quite promising when $t$ is large and it is actually loose. For Figure~\ref{fig:qftexam}(b) which corresponds to the upper bound of $P(4)$, there may be $\frac{1}{t}$ of remote CRZ gates, i.e., $\text{CRZ}_{43}$ and $\text{CRZ}_{32}$ not in a block with 4 remote CX gates at the first glance. But we can actually combine $\text{CRZ}_{43}$ and $\text{CRZ}_{32}$ to form a 4-REM-CX block since there are no other remote gates between them. This indicates that QFT has more abundant burst communication than the upper bound suggests.
\begin{figure}
\caption{QAOA program with two nodes and three qubits per node. Parameters omitted for simplicity. (a) inter-node communication number $r=3$. (b) $r=4$.}
\label{fig:qaoaexam}
\end{figure}
Similarly, for the QAOA program, we assume $k$ nodes and $t$ qubits per node. We also suppose $r$ remote ZZ interactions between any two nodes. Figure~\ref{fig:qaoaexam} shows the QAOA program with $k=2$ and $t=3$. Likewise, $P(2) = 0$ since each ZZ interaction is compiled into two CX gates, as shown in Figure~\ref{fig:qaoaexam}(a). For every two nodes, the qubit layout to minimize $len(\epsilon(ZZ))$ for each ZZ interaction is to make every two ZZ interactions have no shared qubits, i.e., not adjacent. However, this layout at most accommodates $t$ ZZ interactions. If $r > t$, the number of ZZ interactions s.t. $len(\epsilon(ZZ)) < 4$ is at most $t-2(r\ mod\ t)$ by examining the gate adjacency. Thus, $P(4) \le \frac{t-2(r\ mod\ t)}{r}$. For example in Figure~\ref{fig:qaoaexam}(b), only $\frac{t-2(r\ mod\ t)}{r} = \frac{1}{4}$ of remote ZZ interactions are not in a 4-REM-CX block.
Generally, if $r > st$ for some integer $s$, $P(2(s+1)) \le \frac{t-2(r\ mod\ t)}{r} < \frac{1}{s}$. This study reveals that burst communication is broadly available in the QAOA program.
We could derive a similar analysis for other programs.
Further numerical evidence for the richness of burst communication in various programs is shown in Figure~\ref{fig:burst-stat}. The next step is to figure out how to utilize the abundant burst communication in distributed programs to optimize the communication overhead, as discussed in the next section.
\subsection{Optimization Opportunities}
To exploit burst communication in distributed quantum programs, we need to answer three key questions:
\paragraph{How to unveil the burst communication?} The burst communication is high-level program information and cannot be deduced simply from the low-level circuit language, especially when
the remote interactions between multiple nodes are all mixed together. For example in Figure~\ref{fig:example}, gate $CX\, q_2;q_4$ between node A and node B is followed by $CX\, q_1;q_6$, which is the interaction between node A and node C. To maximize the benefits of burst communication, we need to discover groups of remote gates in disordered quantum circuits.
\paragraph{How to select the best communication scheme?}
Burst communication comes in various forms. Cat-Comm may not always be better than TP-Comm for burst communication, unlike the single CX case. For example in Figure~\ref{fig:example}, if we use Cat-Comm to implement the last three remote CX gates between $q_3$ and node A, three EPR pairs are needed. However, with TP-Comm to teleport $q_3$ to node A, at most two EPR pairs are needed.
Thus, to reduce the communication cost, we should examine the pattern of burst communication and choose the communication scheme wisely.
\paragraph{How to schedule burst communication?} Finally, we need to schedule the execution of burst communication blocks. If we arrange all burst communication in a sequential way, the large time overhead would impose non-negligible decoherence errors on quantum states.
As a result, we should maximize the parallelism in burst communication to generate high-fidelity output. To achieve this goal,
we must first identify the relationships between communication blocks and then reduce the gaps caused by them adaptively.
\section{{\frameworkNameSpace} Framework}
In this section, we first give an overview of the {\frameworkNameSpace} framework and then introduce each component in detail.
\subsection{Design overview}
We propose the \textit{\frameworkName} framework as shown in Figure~\ref{fig:designoverview}.
{\frameworkName} focuses on the communication optimization of distributed quantum programs and serves as the back-end of front compiling flows like mapping qubits to quantum nodes. We would adopt existing technologies for these front compiling stages, as we would see in Section~\ref{sect:eval}.
To optimize the communication overhead in distributed programs,
{\frameworkName} comes with three stages to utilize the burst communication. First, it aggregates remote two-qubit gates by gate commutation. Gate commutation is quite common in quantum programs~\cite{Nam2017AutomatedOO}. Commutable gates, on the one hand, may be ordered arbitrarily and hide the burst communication. On the other hand, we could also utilize gate commutation to uncover burst communication blocks. In this stage, a pre-processing step is used to identify burst communication, and a linear merge step is employed to combine isolated burst communication blocks.
Second, it assigns an optimal communication scheme for each burst communication. We observe that the pattern of burst communication impacts the efficiency of communication schemes. Cat-Comm is less expensive for some patterns, while TP-Comm may be more cost-effective for others. It is thus important to examine the communication patterns and consider both Cat-Comm and TP-Comm for hybrid communication, rather than focusing on one scheme.
Third, it performs a block-level schedule of burst communication.
It is possible to run communication blocks with shared nodes or qubits concurrently or shorten the quantum state transfer path across quantum nodes for specified communication patterns. Combined with these optimizations,
a greedy schedule is effective for burst communication blocks.
\input{img/rule}
\begin{algorithm}[h]
\footnotesize
\SetAlgoLined
\KwIn{An array of communication blocks $blk\_list$}
\KwOut{Merged communication blocks $blk\_list\_merge$}
$blk\_list\_merge = [\,]$\;
$blk = blk\_list[0]$ \;
\While{there are blocks in $blk\_list$ not visited}{
$non\_commute\_gates = []$\;
\For{$blk\_next$ in unvisited blocks of $blk\_list$}{
\tcp{Attempt merge $blk$ to $blk\_next$}
\For{$gate$ between $blk$ and $blk\_next$}{
\uIf{$gate$ is single-qubit and not commutes with $blk$}{
$non\_commute\_gates.append(gate)$\;
}
\uIf{$gate$ is two-qubit}{
check if $gate$ is commutable with $non\_commute\_gates$ and $blk$\;
\uIf{not commutable}{
\uIf{$gate$ is in-node two-qubit}{
$non\_commute\_gates.append(gate)$;
} \uElse{
break\;
}
}
}
}
$blk = $merge $blk$, $non\_commute\_gates$ and $blk\_next$\;
}
\uIf{the above merge failed}{
Try to merge $blk\_next$ to $blk$ similarly\;
\uIf{succeeds}{
$blk = $merge $blk$, $non\_commute\_gates$ and $blk\_next$\;
} \uElse{
$blk = blk\_next$\;
}
}
}
output the merged blocks and adjust the order of commutable gates\;
\caption{Linear merge procedure}
\label{alg:linear-merge}
\end{algorithm}
\begin{figure}
\caption{Communication aggregation for the example program in Figure~\ref{fig:example}
\label{fig:commagg}
\end{figure}
\subsection{Communication Aggregating}
Burst communication is prevalent in distributed programs, but may not be immediately available due to two factors: CX gates may be scattered across the program, and whether CX gates are remote depends on the qubit mapping to quantum nodes.
To uncover hidden burst communications, we need to rewrite the circuit and aggregate remote CX gates.
Figure~\ref{fig:xrule} summarizes the X-rotation-centered rewriting rules used for gate commutation. Rules for other rotation axes can be obtained by similar transformation.
Below are the main steps to aggregate remote gates based on these rules.
\paragraph{Preprocessing:} The first step is to identify the qubit-node pair of burst communication.
We start with the qubit-node pair associated with the most remote gates as it would likely lead to a large burst communication block. For example in Figure~\ref{fig:example}, the chosen qubit-node pair is ($q_3$, node A) as it is associated with 5 remote CX gates. We then search for consecutive remote CX gates related to this qubit-node pair.
This step would result in many isolated communication blocks, for example in Figure~\ref{fig:commagg}(a), we obtain four small blocks.
\paragraph{Linear merge:} The next step is to merge isolated small communication blocks obtained in the preprocessing.
As illustrated in Algorithm~\ref{alg:linear-merge}, we merge related communication blocks in a linear and greedy manner.
For communication blocks \circlenum{1}, \circlenum{2}, \circlenum{3}, \circlenum{4} in Figure~\ref{fig:commagg}(a),
we can easily merge block \circlenum{1} and \circlenum{2} since only single-qubit gates exist between those two blocks. However, we can not merge block \circlenum{2} and block \circlenum{3} because gate $CX\, q_5,q_3$ is commutable with neither block \circlenum{2} nor block \circlenum{3}. Finally, as shown in Figure~\ref{fig:commagg}(b), we obtain two larger communication blocks.
\paragraph{Iterative refinement:} Then we merge communication blocks of other qubit-node pairs in descending order of their number of remote gates until no improvement is made. The final result of communication aggregation is shown in Figure~\ref{fig:commagg}(c).
\subsection{Communication Assignment}\label{sect:blocking}
With burst communication blocks, the next optimization is to find the best way to execute them.
We address this problem
by first examining the pros and cons of Cat-Comm and TP-Comm, and then assigning the optimal communication scheme based on the pattern analysis of burst communication blocks. Since we assume only two communication qubits in each quantum node, the communication patterns discussed here center on interactions between one qubit and one node. Extending burst communication to the node-to-node situation is promising when communication qubits are plentiful. We leave it for future work.
\paragraph{Cat-Comm vs. TP-Comm:}
Suppose we have a burst communication block between a qubit $q_1$ in node A and several qubits in node B, with a total of $n$ remote CX gates in the block. If the block can be executed by a single call to Cat-Comm, the savings on EPR pairs would be up to $n$ times, compared to executing each remote CX gate individually. However, as discussed below, not all communication blocks can be cheaply executed via Cat-Comm. Compared to Cat-Comm, the savings on ERP pairs with TP-Comm is at most $\frac{n}{2}$ times as TP-Comm requires two EPR pairs to execute any burst communication block: one to teleport $q_1$ to node B, the other to release the occupancy of $q_1$ on the communication qubit in node B. For simplicity, we use the other EPR pair to teleport $q_1$ back to node A.
We postpone to
Section~\ref{sect:schedule} to handle the case that teleporting $q_1$ to some other node is better than moving back.
Overall, Cat-Comm provides higher ERP pair savings for specific burst communication blocks, while TP-Comm can handle an arbitrary communication block with up to two EPR pairs.
\begin{figure}
\caption{Two primitive communication patterns (a)(b) and the variant (c).}
\label{fig:pattern1}
\end{figure}
\begin{figure}
\caption{The transformation between communication patterns by using Hadamard gates.}
\label{fig:patterntransform}
\end{figure}
\begin{figure*}
\caption{(a) The result of the communication assignment pass. (b) The result of the communication schedule pass.}
\label{fig:commassignsched}
\end{figure*}
\paragraph{Pattern analysis:}
Figure~\ref{fig:pattern1}(a)(b) shows two primitive patterns for qubit-to-node burst communication.
For the unidirectional communication pattern in Figure~\ref{fig:pattern1}(a) where one qubit (i.e., $q_1$) always serves as the control qubit, the communication block can be implemented by Cat-Comm with only one EPR pair if
no single-qubit gate on the control qubit separates two-qubit gates~\cite{cat_entangle}. For example, one call of Cat-Comm can handle the gate sequence $CX\,q_1,q_1';\,CX\,q_1,q_2'$ , but cannot address $CX\,q_1,q_1';\,H\,q_1;\,CX\,q_1,q_2'$ due to the middle H gate.
To optimize this communication pattern with Cat-Comm, we should remove single-qubit gates on the control qubit. When they are not removable, we resort to TP-Comm.
A varied unidirectional pattern in which $q_1$ always serves as the target qubit, as shown in Figure~\ref{fig:pattern1}(c), also occurs frequently in distributed quantum programs. This pattern can be transformed into the pattern in Figure~\ref{fig:pattern1}(a) by applying a series of Hadamard gates, as shown in Figure~\ref{fig:patterntransform}(a).
In contrast to unidirectional patterns, Figure~\ref{fig:pattern1}(b) shows a bidirectional pattern in which $q_1$ serves as both control qubit and target qubit. A block in this pattern cannot be executed by a single call of Cat-Comm as Cat-Comm cannot transfer the state of target qubits. Even if we transform it to the unidirectional pattern in Figure~\ref{fig:patterntransform}(b) with Hadamard gates, single-qubit gates on the control qubit still prevent a cheap implementation by Cat-Comm. In fact, for the block in Figure~\ref{fig:patterntransform}(b), TP-Comm is more efficient as it only requires two EPR pairs, while Cat-Comm requires three EPR pairs.
To summarize, for unidirectional patterns in Figure~\ref{fig:pattern1}(a)(c), we will try Cat-Comm first, while for the bidirectional pattern in Figure~\ref{fig:pattern1}(b), TP-Comm is preferred.
\paragraph{Communication assignment:}
Now, we are ready to assign an optimal communication scheme, either Cat-Comm or TP-Comm, to each burst communication block.
Considering Figure~\ref{fig:commagg}(c) as an example, we assign Cat-Comm to unidirectional blocks \circlenum{1}, \circlenum{6} and \circlenum{7}, and assign TP-Comm to bidirectional blocks \circlenum{2}, \circlenum{4} and \circlenum{5}. For \circlenum{3}, although being unidirectional, it cannot be executed by one call of Cat-Comm as there is a $T^{\dagger}$ gate on the control qubit between two CX gates. Since executing it with either Cat-Comm or TP-Comm requires two EPR pairs, we set the TP-Comm assignment as default. The finalized assignment is shown in Figure~\ref{fig:commassignsched}(a).
\subsection{Communication Scheduling}\label{sect:schedule}
After optimizing the count of remote communications, we then schedule the execution of burst communication blocks to
reduce the total execution time of the distributed program and reduce the impact of decoherence. Based on the quantitative data shown in Table~\ref{tab:quantdata}, the preparation of remote EPR pairs is the most time-consuming one among various operations and hence should be carefully optimized to hide its latency. While the quantitative data may vary across quantum devices, the schedule design in this section should be also effective.
\begin{table}[htbp]
\centering
\small
\renewcommand*{\arraystretch}{1}
\begin{tabular}{|l|c|l|}
\hline
Operation & Variable Name & Latency \\ \hline
Single-qubit gates & $t_{1q}$ & $\sim$ 0.1 CX \\ \hline
CX and CZ gates & $t_{2q}$ & 1 CX \\ \hline
Measure & $t_{ms}$ & 5 CX \\ \hline
EPR preparation
& $t_{ep}$ & $\sim$ 12 CX \\ \hline
One-bit classical comm & $t_{cb}$ & $\sim$ 1 CX \\ \hline
\end{tabular}
\caption{The quantitative latency data of operations in distributed quantum programs, extracted from~\cite{isailovic2006interconnection, correa2018ultra}. All latencies are normalized to CX counts.}
\label{tab:quantdata}
\end{table}
The designs here aim to maximize block-level parallelism and shorten the latency of sequential execution by fusion.
\paragraph{More block-level parallelism:}
The essence of scheduling is to maximize the parallelism in a circuit.
For burst communication blocks without nodes or qubits in common, they can be concurrently executed in nature. For blocks with shared nodes or qubits, their parallelism is limited by their commutability, as well as the communication resources each node holds. With the constraint that each node can establish only two communications in parallel, there is little room for lazy operations, and we adopt a greedy strategy to execute commutable blocks, i.e., execute as many blocks as possible simultaneously, as soon as EPR pairs are prepared.
\begin{figure}
\caption{The schedule optimization for commutable Cat-Comm blocks, with shared qubit or node.
}
\label{fig:pipesched}
\end{figure}
\begin{figure}
\caption{The schedule optimization for TP-Comm blocks. Aligned qubit teleportation in (b) is better than the independent qubit teleportation in (a).
}
\label{fig:greedytp}
\end{figure}
For Cat-Comm blocks, we can execute two commutable blocks in parallel at most if they share nodes, as shown in Figure~\ref{fig:pipesched}. For TP-Comm blocks, the situation is complex as each TP-Comm blocks require two EPR pairs. For two commutable TP-blocks, rather than prioritizing the completion of one TP-comm as in Figure~\ref{fig:greedytp}(a), we observe that parallelism can be enabled by communication alignment, as shown in Figure~\ref{fig:greedytp}(b). Compared to Figure~\ref{fig:greedytp}(a), Figure~\ref{fig:greedytp}(b) aligns the qubit teleportation of the two blocks, leading to a latency saving of $t_{block}+2t_{tele}$. This TP-Comm alignment technique can be generalized to the case of $n$ commutable TP-Comm blocks (any two blocks may share common nodes). With TP-Comm alignment, the total latency saving can be up to $(n-1)(t_{block}+2t_{tele})$ (e.g., if those TP-Comm blocks are on nodes $\{A_1, A_2\}, \{A_2, A_3\},\cdots, \{A_n, A_{n+1}\}$ respectively).
\begin{figure}
\caption{The schedule optimization for TP-Comm blocks. Cyclic qubit teleportation in (b) is better than the SWAP-style qubit teleportation in (a).
}
\label{fig:tokenpass}
\end{figure}
\paragraph{Fusion of sequential blocks:}
Sometimes communication blocks have to be executed in sequence. However, if the teleported qubits in TP-Comm blocks are the same, we can optimize their executions by fusing the teleportations, as shown in Figure~\ref{fig:tokenpass}. Figure~\ref{fig:tokenpass}(a) shows a simple schedule where each TP-Comm is executed independently. As each node has only two communication qubits, we need to wait for $t_{ep}$ before executing the next TP-Comm block. In contrast, Figure~\ref{fig:tokenpass}(b) fuses the teleportations between quantum nodes, forming a cycle: $A \to B \to C \to A$. With fusion, the number of teleportations is reduced by one and the overall execution time is reduced by $t_{ep}+t_{tele}$, where $t_{tele}$ is the time to teleport one qubit (about 8 CX time as shown in Figure~\ref{fig:qucomm}(b)). Generally, if we have $n$ TP-Comm blocks with the same teleported qubit, the total number of teleportation would be reduced by $n-1$, and the saving of overall latency would be $(n-1)(t_{ep}+t_{tele})$.
From another view, the fusion also optimizes the token passing problem in classical distributed computing~\cite{van2002distributed}, which also appears in Section~\ref{sect:blocking}, about whether to move the teleported qubit in TP-Comm back or to another node.
With the designs above, the communication schedule pass should apply block-level commutation analysis to unveil the patterns discussed above and then apply corresponding optimizations. We omit the details since this procedure is very similar to the communication aggregation except working at the block level.
With all those optimizations applied, Figure~\ref{fig:commassignsched}(b) shows the optimized communication schedule for the program in Figure~\ref{fig:example}. In total, 2.4x latency saving is achieved compared to executing each remote CX gate independently.
\section{Evaluation}\label{sect:eval}
In this section, we first compare the performance of {\frameworkName} to the baseline method and then evaluate the effect of each optimization pass in {\frameworkName}. We finally perform a sensitivity analysis on {\frameworkName} to study how its performance evolves as the program configuration changes.
\subsection{Experiment Setup}
\paragraph{Metric} The first metric we considered is the number of issued remote communications. Each remote communication would consume one remote EPR pair for both Cat-Comm and TP-Comm. To avoid the ambiguity on the cost of TP-Comm, we say TP-Comm needs two communications (i.e., two EPR pairs) to execute one burst communication block, with one of the communications handling its dirty side-effect.
The number of remote communications models the resource overhead of executing distributed programs and a lower value is favored.
The second metric is the maximum number of remote two-qubit gates executed through one communication. For TP-Comm blocks, this number is averaged on two communications. We denote this metric by `Peak \# REM CX'.
This metric models the communication throughput of information and a higher value is preferred.
Finally, we consider two metrics that model the relative performance, in communication cost and program latency respectively, of {\frameworkName} to baselines. The first one is `improv. factor', which is defined to be `total communication \# by baseline/total communication \# by \frameworkName'. The second one is `LAT-DEC factor' and is defined to be `program latency by baseline/program latency by \frameworkName'. We hope these two metrics to be as large as possible.
\paragraph{Baseline} For the baseline method, we implement the compiler~\cite{Ferrari2021CompilerDF} which only exploits the Cat-Comm scheme for remote CX gates and does not consider burst communication. To reduce the program latency, the baseline adopts a greedy scheduling method, i.e., executing operations as soon as possible.
For both the baseline and {\frameworkName}, we map qubits to distributed quantum nodes by the `Static Overall Extreme Exchange' strategy studied in ~\cite{time-slice}.
\paragraph{Platforms} We perform all experiments on a Ubuntu 18.04 server with a 6-core Intel E5-2603v4 CPU and 32GB RAM. Other software includes Python 3.8.3 and Qiskit 0.18.3~\cite{Qiskit}.
\paragraph{Benchmark programs} We consider two categories of benchmark programs, as shown in Table~\ref{tab:benchmark}. The first category of benchmarks are function-specific, i.e., they focus on implementing specific elementary functions, e.g., arithmetic operations and Fourier transformation. These quantum programs are often used as the building blocks of large quantum applications. The second category of benchmarks are application-driven. These programs usually target at solving real-world problems, e.g., Bernstein-Vazirani (BV) algorithm, Quantum Approximate Optimization algorithm (QAOA), and Unitary Coupled Cluster ansatzes (UCCSD). Specifically, we choose the graph maxcut problem for the QAOA test programs, and for the UCCSD programs, we select molecules $\text{LiH}, \text{BeH}_2$, and $\text{CH}_4$ which correspond to 8, 12, and 16 particles (thus qubits), respectively.
All benchmark programs used in the evaluation are collected from IBM Qiskit~\cite{Qiskit} and RevLib~\cite{revlib}.
\begin{table}[t]
\centering
\resizebox{0.4\textwidth}{!}{
\renewcommand*{\arraystretch}{1.4}
\begin{tabular}{|p{1.0cm}|p{1.5cm}|p{1.0cm}|p{1.3cm}|p{1.0cm}|p{1.0cm}|p{1.55cm}|} \hline
Type & Name & \# qubit & \# node & \# gate & \# CX & \# REM CX \\ \hline
\multirow{9}{1.0cm}{Build-ing Blocks} & \multirow{3}{1.5cm}{Multi-Controlled Gate (MCTR)} & 100 & 10 & 10640 & 4560 & 1680 \\ \cline{3-7}
& & 200 & 20 & 21840 & 9360 & 3568 \\ \cline{3-7}
& & 300 & 30 & 33040 & 14160 & 5632 \\ \cline{2-7}
& \multirow{3}{1.5cm}{Ripple-Carry Adder (RCA)} & 100 & 10 & 1569 & 785 & 220 \\ \cline{3-7}
& & 200 & 20 & 3169 & 1585 & 662 \\ \cline{3-7}
& & 300 & 30 & 4769 & 2385 & 820 \\ \cline{2-7}
& \multirow{3}{1.5cm}{Quantum Fourier Transform (QFT)} & 100 & 10 & 40100 & 20000 & 9000 \\ \cline{3-7}
& & 200 & 20 & 160200 & 80000 & 38000 \\ \cline{3-7}
& & 300 & 30 & 360300 & 180000 & 87000 \\ \hline
\multirow{9}{1.0cm}{Real World Appli-cations} & \multirow{3}{1.5cm}{Bernstein Vazirani (BV)} & 100 & 10 & 265 & 65 & 56 \\ \cline{3-7}
& & 200 & 20 & 535 & 135 & 126 \\ \cline{3-7}
& & 300 & 30 & 803 & 203 & 194 \\ \cline{2-7}
& \multirow{3}{1.5cm}{QAOA} & 100 & 10 & 6000 & 4000 & 3144 \\ \cline{3-7}
& & 200 & 20 & 24000 & 16000 & 14076 \\ \cline{3-7}
& & 300 & 30 & 54000 & 36000 & 32896 \\ \cline{2-7}
& \multirow{3}{1.5cm}{UCCSD} & 8 & 4 & 3129 & 1420 & 900 \\ \cline{3-7}
& & 12 & 6 & 40659 & 19142 & 15136 \\ \cline{3-7}
& & 16 & 8 & 129829 & 64956 & 53426 \\ \hline
\end{tabular}
}
\caption{Benchmark programs. The qubits are evenly distributed across quantum nodes. The number of remote CX gates (\# REM CX) is computed on the qubit mapping by `Static Overall Extreme Exchange'~\cite{time-slice}.}
\label{tab:benchmark}
\end{table}
\begin{figure}
\caption{Burst communications by \frameworkName: Pr[X] = Pr[one communication carries >= X\hspace{3pt}
\label{fig:burst-stat}
\end{figure}
\subsection{Compared to Baseline}
We evaluate both {\frameworkName} and the baseline method on benchmark programs in Table~\ref{tab:benchmark}. The results of {\frameworkName} and its relative performance to the baseline are shown in Table~\ref{tab:comm-cost}.
\paragraph{Burst communication statistics:} Figure~\ref{fig:burst-stat} shows the distribution of burst communications assembled by {\frameworkName}. This distribution is closely related to the inverse-burst distribution discussed in Section ~\ref{sect:burstcomm} but is easier to compute. We can see that burst communications exist widely in various distributed quantum programs, no matter in building-block circuits (Figure~\ref{fig:burst-stat}(a)) or in real-world applications (Figure~\ref{fig:burst-stat}(b)). Moreover, Figure~\ref{fig:burst-stat} demonstrates the effectiveness of {\frameworkName} in unveiling burst communications. In Figure~\ref{fig:burst-stat}, the communications that each carries $\ge2$ remote CX gates account for 76.8\% of the total remote communications, on average.
\paragraph{Communication cost:} {\frameworkName} achieves significant communication cost reduction on the benchmark programs.
Compared to the baseline method, {\frameworkName} reduces the number of remote communications by a factor of 4.1x on average, up to 9.2x. The peak communication throughput (i.e., `Peak \#\,REM CX') by {\frameworkName} is 8.8x on average and up to 18x of that by the baseline.
These improvements indicate that {\frameworkName} can efficiently discover and utilize burst communications in distributed quantum programs, transferring more information in each communication than the baseline method.
The good communication performance of {\frameworkName} comes from two factors: the aggregation of remote CX gates and the hybrid implementation of burst communications by using both Cat-Comm and TP-Comm. We will further elaborate on this point in Section~\ref{sect:optianaly}.
\paragraph{Latency:} {\frameworkName} also achieves significant latency reduction on benchmark programs.
Compared to the baseline method, {\frameworkName} reduces the program execution time by a factor of 3.5x on average, up to 7.1x, as shown in Table~\ref{tab:comm-cost}.
The trend of latency reduction is closely related to the trend of communication cost reduction. This is as expected because {\frameworkName} keeps the local parallelism in the program when aggregating remote interactions.
\begin{table}[tbp]
\centering
\footnotesize
\resizebox{0.48\textwidth}{!}{
\renewcommand*{\arraystretch}{1.2}
\begin{tabular}{|p{2.cm}|p{1.35cm}|p{1.35cm}|p{1.1cm}|p{1.0cm}|p{1.29cm}|} \hline
{
Name} & {
Tot Comm} & {
TP-Comm} & Peak\,\# REM\,CX & Improv. factor & LAT-DEC factor \\ \hline
MCTR-100-10 & 533 & 220 & 10 & 3.15 & 3.27 \\\hline
MCTR-200-20 & 972 & 418 & 10 & 3.67 & 3.83 \\\hline
MCTR-300-30 & 2044 & 1112 & 10 & 2.76 & 2.88 \\\hline
RCA-100-10 & 79 & 54 & 5.5 & 2.78 & 3.34 \\\hline
RCA-200-20 & 469 & 224 & 5.5 & 1.41 & 2.10 \\\hline
RCA-300-30 & 410 & 204 & 5.5 & 2.00 & 3.30 \\\hline
QFT-100-10 & 2068 & 1784 & 18 & 8.70 & 6.53 \\\hline
QFT-200-20 & 8351 & 7566 & 18 & 9.10 & 6.98 \\\hline
QFT-300-30 & 18835 & 17348 & 18 & 9.24 & 7.13 \\\hline
BV-100-10 & 9 & 0 & 8 & 6.22 & 4.33 \\\hline
BV-200-20 & 19 & 0 & 8 & 6.63 & 4.63 \\\hline
BV-300-30 & 29 & 0 & 8 & 6.69 & 4.69 \\\hline
QAOA-100-10 & 1448 & 266 & 6 & 2.17 & 1.83 \\\hline
QAOA-200-20 & 6787 & 728 & 8 & 2.07 & 1.79 \\\hline
QAOA-300-30 & 16053 & 1138 & 6 & 2.05 & 1.69 \\\hline
UCCSD-8-4 & 464 & 0 & 4 & 1.94 & 1.74 \\\hline
UCCSD-12-6 & 8973 & 0 & 4 & 1.69 & 1.55 \\\hline
UCCSD-16-8 & 33303 & 0 & 5 & 1.60 & 1.50 \\\hline
\end{tabular}
}
\caption{The results of {\frameworkName} and its relative performance to the baseline. The name column are acronyms of test programs in Table~\ref{tab:benchmark}.}
\label{tab:comm-cost}
\end{table}
\subsection{Compared to GP-based Compiler}
We further compare {\frameworkName} to the graph-partition-based (GP-based) compiler~\cite{time-slice}.
A GP-based compiler converts remote interactions to local interactions by swapping qubits with a strategy derived from graph partition algorithms.
To reduce the communication cost and program latency of the GP-based compiler, we utilize TP-Comm for swapping qubits since TP-Comm requires only two communications for one remote SWAP gate, one communication less than using Cat-Comm. We denote this version of the GP-based compiler by \textit{GP-TP}. Once again, for GP-TP, we adopt the as-soon-as-possible schedule strategy in~\cite{Ferrari2021CompilerDF}.
As shown in Figure~\ref{fig:gptp}, {\frameworkName} achieves significant reduction in both communication cost and program latency, compared to GP-TP. Specifically, {\frameworkName} reduces the communication cost by a factor of 3.3x on average, up to 12.9x. It also reduces the program execution time by a factor of 4.3x on average, up to 10.3x. On the side of information theory, {\frameworkName} improves the performance by enabling a higher throughput of information. Each remote communication in GP-TP carries less than two remote CX gates which is much smaller than {\frameworkName}. On the algorithmic side, {\frameworkName} reduces unnecessary qubit movement by taking advantage of burst communication. For example, for a potential burst communication between $q_1$ and node B, if there are some commutable remote CX gates between $q_1$ and node C lying in between and interrupting the communication block between $q_1$ and node B, the GP-TP method needs to move $q_1$ to node B first, then to node C and back to node B again. However, with burst communication, we only need to first move $q_1$ to node B, and then to node C.
\begin{figure}
\caption{Compared to GP-TP. Results are averaged over different configurations of \#\,qubit and \#\,node in Table~\ref{tab:benchmark}
\label{fig:gptp}
\end{figure}
\subsection{Optimization Analysis}\label{sect:optianaly}
\begin{figure*}
\caption{(a)-(c) The effects of the proposed optimizations. Bars with different colors denote different configurations of (\#qubit, \#node).
For (a)(b), the y-axis is the ratio of \# remote communications. For (c), the y-axis is the ratio of program latency. (d)(e) The effects of \#\,qubit and \#\,node on the improv. factor of \frameworkName. The test program in (d)(e) is MCTR.}
\label{fig:opti}
\end{figure*}
In this section, we further explore and analyze the effect of each optimization in \frameworkName. For each analysis, we change only one component of {\frameworkName} at a time, with other components fixed, to isolate the effect of each component/optimization.
\paragraph{The effect of communication aggregation:} Table~\ref{tab:comm-cost} demonstrates the benefit of communication aggregation compared to the baseline. Here we further demonstrate the necessity of considering gate commutation in the aggregation pass. Figure~\ref{fig:opti}(a) shows the communication cost comparison between the aggregation without gate commutation and the aggregation used in {\frameworkName}. For the programs in Figure~\ref{fig:opti}(a), {\frameworkName} reduces the communication cost by a factor of 5.5x on average, up to 6.7x, compared to the aggregation without gate commutation.
Gate commutation is indispensable for discovering burst communications, not only because multi-qubit gates are often scattered in quantum circuits, but also due to the uncertainty of qubit mapping to quantum nodes (the uncertainty of whether a CX is remote or local).
\paragraph{The effect of hybrid communication assignment:} We further demonstrate the importance of considering both Cat-Comm and TP-Comm for burst communication. Figure~\ref{fig:opti}(b) shows the communication cost comparison between the communication assignment with Cat-Comm only and the hybrid assignment scheme in {\frameworkName}. The Cat-Comm only method is extended from the specialized compiler~\cite{Diadamo2021DistributedQC} for distributed VQE.
For the programs in Figure~\ref{fig:opti}(b), {\frameworkName} reduces the communication cost by a factor of 2.8x on average, up to 4.6x, compared to the Cat-Comm only method. The key enabler for the hybrid scheme in {\frameworkName} is that Cat-Comm only applies to few communication patterns and for the cases that Cat-Comm cannot apply, TP-Comm would be more efficient.
\paragraph{The effect of communication scheduling:} We then study the effect of the communication scheduling optimization in {\frameworkName}.
Figure~\ref{fig:opti}(c) shows the latency comparison between {\frameworkName}'s scheduling, denoted by burst-greedy, and the greedy (as-soon-as-possible) scheduling for communication blocks.
For the programs in Figure~\ref{fig:opti}(c), the burst-greedy method reduces the program latency by a factor of 1.4x on average, up to 1.6x, compared to the general greedy schedule.
The effectiveness of {\frameworkName} for scheduling burst communication stems from its smart utilization of communication qubits, especially for TP-Comm blocks, as discussed in Section~\ref{sect:schedule}.
\subsection{Sensitivity Analysis}
The performance of {\frameworkName} may be affected by some external factors, e.g., the number of input qubits and the number of computing nodes.
In this section, we study how the performance of {\frameworkName} varies with those factors. We focus on `improv. factor' here, and the variation of `LAT-DEC factor' would follow a similar trend.
\paragraph{The effect of \#\,qubit:} Figure~\ref{fig:opti}(d) shows how the improv. factor of {\frameworkName} changes with the number of qubits. As shown in the figure, the improv. factor converges when \# qubit/\# node is large.
This may be due to the fact that the number of burst communication blocks also increases when the total number of remote multi-qubit gates grows with the number of qubits. Such behavior is preferable because it illustrates that {\frameworkName} can provide a consistent reduction for the communication cost as the number of qubits grows.
\paragraph{The effect of \#\,node:} Figure~\ref{fig:opti}(e) shows how the improv. factor of {\frameworkName} changes with the number of nodes. In this figure, the performance of {\frameworkName} deteriorates when \# qubit/\# node is small. This is because it is harder to find large communication blocks when the number of qubits in each node is limited to be small.
Therefore we should avoid using too many nodes for distributing quantum programs because in such a case the remote multi-qubit gates would proliferate and there is little chance to execute those remote interactions collectively, given the fact that the number of communication qubits in each node is only two.
\section{Discussion and Future Work}
To the best of our knowledge, this paper is the first attempt that formalizes burst communication in distributed quantum programs.
We discover a large number of burst communications hidden in various distributed quantum programs and propose the first modular framework to uncover these burst communications and use them to optimize the communication overhead.
We argue that the formalization of burst communication and the modular solution proposed in this paper unveil new opportunities for communication optimization in DQC and would potentially inspire a series of works for overcoming DQC's communication problem.
Although we show that the proposed framework significantly surpasses existing works in optimizing the communication overhead of distributed quantum programs, there is still much space left for potential improvements.
\paragraph{Extending to general collective communication} This paper only considers the near-term DQC where communication qubits are supposed to be limited. In such a case, we are restricted to studying the qubit-to-node burst communication, which is a special case of the general collective communication, involving a group of nodes.
Assuming the availability of more communication qubits in the future, we could consider node-to-node collective communication which offers a potential optimization opportunity as we can now aggregate small qubit-to-node burst communication blocks into a larger one. Besides, for the fusion operation in the communication schedule optimization, we can also extend it to node-to-node communication blocks.
\paragraph{Co-designing with front compiling stages} The proposed framework is designed to be easily pluggable into existing compiling flows. But we could also couple it with front compiling stages to achieve further optimization. For example,
existing compilers include a pass to add SWAP gates to change the qubit layout to optimize circuit metrics. We could co-design with this pass to maximize the number and size of burst communications. Besides, in the case where burst communication is deeply hidden, we could also consider using unitary synthesis to create burst communication in the gate decomposition pass.
Finally, we could co-design with the qubit mapping pass to achieve a balance of communication overhead and device utilization rate, as shown in Figure~\ref{fig:opti}(d)(e).
\paragraph{Combining with quantum error correction} Since DQC involves quantum communication which is far more noisy than local quantum gates, reinforcing the whole distributed quantum system with quantum error correction (QEC) becomes vital for future DQC.
One promising way to implement QEC in DQC is to encode one logical qubit in each node, and use quantum communication to implement logical operations between logical qubits. In this case, the CX gate between logical qubits would involve a large number of physical qubits simultaneously and provide great opportunities for burst communication optimization. Besides, communications coming from magic state distillation are also worth considering.
\section{Related Work}
Most existing quantum compilers~\cite{Li2019TacklingTQ, Qiskit, Amy2019staqAFQ, Khammassi2022OpenQLA, Sivarajah2020tketAR} focus on the compilation of programs within a single quantum computer. Extending these works to DQC cannot achieve high information throughput per quantum communication, as in the compiler proposed by Ferrari et al.~\cite{Ferrari2021CompilerDF}. Baker et al.~\cite{time-slice} propose using the more informative remote SWAP gates to replace all remote CX gates in distributed quantum programs and obtain a higher throughput. Diadamo et al. \cite{Diadamo2021DistributedQC} further increase the communication throughput by considering multiple-qubit control-unitary blocks. However, their work requires specialized circuit representation and cannot optimize general quantum programs.
Moreover, all these works do not consider the burst communication and related optimizations proposed in this paper.
Another line of work executes distributed quantum programs in a hybrid way. Tang et al.\cite{cutQC} propose a way to execute quantum programs in distributed computing nodes but without inter-node communication. To overcome the expressibility loss due to no inter-node communication,
their work relies heavily on classical post-processing techniques and cannot be extended to large-scale quantum programs.
Other quantum communication-related works focus on building robust quantum communication networks~\cite{QNrouting1,QNrouting2,QNrouting3,QNrouting4} or reducing the resource consumption of existing quantum communication techniques~\cite{repeater12,repeater13,repeater14,repeater15,repeater16}. These works are orthogonal to this paper.
\section{Conclusion}
As in classical distributed computing, the inter-node communication overhead bottlenecks distributed quantum computing. Existing compilers~\cite{Ferrari2021CompilerDF, Diadamo2021DistributedQC, time-slice} for distributed programs either treat the inter-node communication like the in-node communication or only provide optimization for gates in the control-unitary form. These works fail to utilize the hidden communication patterns in distributed quantum programs. To overcome the shortcomings of existing compilers, this paper explores various distributed quantum programs and identifies burst communication for the first time. Burst communication is a qubit-node communication pattern that widely exists in many distributed programs.
Based on burst communication, we propose the framework, {\frameworkName}, which is proved to be efficient in cutting down inter-node communication overhead, by comprehensive evaluations on diverse distributed benchmarks.
The proposed framework can be easily integrated into existing compiling flows of quantum programs and would benefit near-term distributed quantum computing.
\end{document} | math |
# -*- encoding: utf-8 -*-
from abjad import *
def test_instrumenttools_transpose_from_sounding_pitch_to_written_pitch_01():
staff = Staff("<c' e' g'>4 d'4 r4 e'4")
clarinet = instrumenttools.ClarinetInBFlat()
attach(clarinet, staff)
instrumenttools.transpose_from_sounding_pitch_to_written_pitch(staff)
assert systemtools.TestManager.compare(
staff,
r'''
\new Staff {
\set Staff.instrumentName = \markup { Clarinet in B-flat }
\set Staff.shortInstrumentName = \markup { Cl. in B-flat }
<d' fs' a'>4
e'4
r4
fs'4
}
'''
) | code |
As Enfield is becoming one of the most sought after London boroughs for residents and increasing number of investors are buying properties in the region. In order to assist investors ensure that they can reap the maximum possible rate of return on investment, Finefair offers the most comprehensive and sought after Guaranteed Rent Enfield specific services possible. Our peerless management solution for properties is designed to meet the flexible needs of any portfolio, giving you maximum income returns on the back of minimal involvement.
Owning a property for investment purposes is a big commitment. The level of investment, however, does not need to be matched by a similar level of time and cost commitment. With the backing of being the preferred supplier for the Local Authority, we at Finefair offer the highest level of property management efficiency available whilst ensuring that your involvement and cost are kept to minimal levels.
The cost of management services is something one might assume to be quite high, in particular when related to something as specialised as a Guaranteed Rent Enfield related service. In truth we at Finefair have implemented a means that makes allowing cost effective property management easily accessible to the investor. Our services are based on a zero rated commission structure and have no monthly fees. This means that we, in effect, offer our services to landlords and property owners at not cost. Finefair are committed to ensuring that you reap the maximum return on your valuable investment at the minimum cost.
We also want you to experience the maximum returns as soon and as regularly as possible when you enter into a relationship with us in the Guaranteed Rent Enfield market. Our services ensure that you receive monthly rental fees whether the property is occupied or not. Finefair also undertakes to make sure you are getting this income revenue stream as soon as possible after you become one of our highly valued clients. The first payments are usually processed within a day or two of agreements being signed.
Finefair offer an end-to-end level of service for property management. As well as taking over the management of utility and Council Tax billing from you, ensuring that they are correctly applied, we also conduct comprehensive monthly inspections of all properties in our management care, ensuring that they are well maintained and looked after at all times.
Finefair’s Guaranteed Rent Enfield services can make sure you enjoy the best rate of return on investment from your property at the lowest cost and lowest level of time commitment.
This entry was posted in Blog Entry on April 13, 2014 by admin. | english |
Nowadays I hear that phrase quite often. I am getting used to it and more so the pronouns. I had mentioned about this before but, just so stress my point, here is a whole blog post dedicated to it.
I go to the supermarket and there the attendees are nice to me “Madam nikusaidie aje?” How can I help you madam? Its so nice! Some of you may think I am getting in over my head or making a big deal over nothing but, I mean, for me, knowing all too well my past and of knowing that I never used to be referred to as such, it gives me such exhilarated feeling whenever someone refers me as such. Simply, feels good! Makes you know inside that its happening. I am actually living the life I have been dreaming about.
When the people close to me, mostly my family and friends who stuck around me, refer to me as 'she' or 'her' it feels really nice. This means that they are internalizing the idea and that its getting easier for them to refer to me as such. I simply love it! You cant help but appreciate it.
I guess this is what most people call 'passing' since I seem to do that very well. Imagine, on about three or four occasions, a former colleague of mine has passed right infront of me, even glancing towards me or rather looking at me and has (seemingly) not recognised me at all! I find that astounding considering that I myself still see me as the same, albeit the hair and make-up! All in all, that must mean something. It must mean that I am making lots of progress. I am happy.
p.s. I cant wait to see an article on a daily paper that is coming out soon. I am told it will be a feature story about Intersexuality and Transsexualism in Kenya and based on a recent workshop that was held here in Nairobi. I am also told that it has stories of intersex and transsexual persons in kenya. It will be a first of its kind. I simply cant wait to see it!
It goes to show how well your transformation has gone. If they can say that without blinking an eye, well, you have really outdone yourself, Madam.
I will start calling you Madam.
"Passing" would mean deception. You're not deceiving anyone. They're seeing the real you! And I don't blame you for feeling good about each "ma'am" you hear or about correct pronouns. I transitioned more than two years ago, and those things still make me feel really good inside. They probably always will!
I'm an alien...Am a little alien! | english |
اشوک نَگر ضلعس مَنٛز کم چھِ تمام ویکسِنیشن سینٹر ۱۸ وُہُر پیٚٹھؠ وٲنٛسہِ خٲطرٕ سٕپُٹنِک دٔیُم ڈوز پیش کران | kashmiri |
Focused on Nature is now headquartered in Arizona just north of Tucson.
This site is small but growing. We hope that it can eventually become a great place to view and purchase nature photography online.
Feel free to share or comment on all photos on our site. You can even leave general comments below.
All pictures in the galleries are for sale. You can choose from prints, merchandise or low res digital downloads.
During the checkout process for prints and merchandise, you may be prompted to crop the photo based on the size you ordered. If you don't like the options, please contact us so that we can custom crop the picture to meet your needs.
Prices for all high resolution digital downloads are negotiable based on the type of rights you would like and how you plan to use the photograph. Please contact us if you are interested in a high resolution file.
If you have any questions about FocusedonNature.com or you just want to say hi, please contact us by clicking on the "CONTACT" link in the main menu.
I am now a fan of FON! | english |
\begin{document}
\baselineskip15pt
\maketitle
\thispagestyle{empty}
\begin{abstract}
Motivated by tumor growth in Cancer Biology, we provide a complete
analysis of existence and non-existence of invasive fronts for the
{\it reduced Gatenby--Gawlinski model}
\begin{equation*}
\partial_t U \,=\, U\bigl\{f(U)-dV\bigr\}\,,\qquad
\partial_t V \,=\, \partial_x \left\{f(U)\,\partial_x V\right\} + r V f(V)\,,
\end{equation*}
where $f(u)=1-u$ and the parameters $d, r$ are positive. Denoting by $(\mathcal{U},\mathcal{V})$ the
traveling wave profile and by $(\mathcal{U}_\pm,\mathcal{V}_\pm)$ its asymptotic states at $\pm\infty$,
we investigate existence in the regimes
\begin{equation*}
\begin{aligned}
&d>1: &\; & \bigl(\mathcal{U}_-,\mathcal{V}_-\bigr)=\bigl(0,1\bigr)
&\textrm{and}\;\;\ \bigl(\mathcal{U}_+,\mathcal{V}_+\bigr)=\bigl(1,0\bigr),\\
&d<1: &\; &\bigl(\mathcal{U}_-,\mathcal{V}_-\bigr)=\bigl(1-d,1\bigr)
&\textrm{and}\;\;\ \bigl(\mathcal{U}_+,\mathcal{V}_+\bigr)=\bigl(1,0\bigr),
\end{aligned}
\end{equation*}
which are called, respectively, {\it homogeneous invasion} and {\it
heterogeneous invasion}. In both cases, we prove that a propagating
front exists whenever the speed parameter $c$ is strictly positive.
We also derive an accurate approximation of the front profile in
the singular limit $c \to 0$.
\end{abstract}
\section{Introduction}\label{sec1}
Biological invasion is one of the basic features of Nature and its potentiality
to modify its structure and its inherent vitality. Sometimes invasion of a
new species can be regarded as a positive event, sometimes as a negative one
depending on the property of the intruder and the invaded, see
\cite{LewiPetrPott16}. Here, motivated by Cancer Biology, we focus on the
appearance of invasion in the form of propagating fronts in {\it tumor growth}.
Precisely, we present a rigorous mathematical analysis of a reaction-diffusion system
composed by two differential equations, for which we prove the existence of
traveling wave solutions that can be interpreted as {\it invasion fronts} of a
cancerous tissue into a healthy one. We urge the reader to pay attention
to the specific form of the nonlinear diffusion term in our system and
the consequences it has on the set of admissible propagation speeds.
\subsection{Genesis of the model}
The original motivation is the analysis of the so-called {\it acid-mediated tumor
growth}, proposed by Otto Warburg as a mechanism responsible for tumor increase
\cite{WarbWindNege27}. Precisely, the so-called {\it Warburg effect} refers to the
observation that --even in aerobic conditions-- cancer cells tend to favor metabolism via
glycolysis rather than the more efficient oxidative phosphorylation pathway, usually
preferred by most other cells of the body \cite{AlfaEtAl14}. A simplified mathematical
description for such a mechanism has been proposed in \cite{GateGawl96}. After an
appropriate rescaling and using the notation $f(s)=1-s$, the one-dimensional version of
the model reads as
\begin{equation}\label{GGsys}
\left\{\begin{aligned}
\partial_t U \,&=\, U\bigl\{f(U) - dW\bigr\}\,, \\
\partial_t V \,&=\, \partial_x \bigl\{f(U)\,\partial_x V\bigr\} + r V f(V) \,, \\
\partial_t W \,&=\, a\,\partial_x^2 W + b(V-W)\,,
\end{aligned}\right.
\end{equation}
where $U = U(x,t)$ represents the (normalized) population of healthy cells, $V=V(x,t)$ is
the (normalized) population of tumor cells, and $W=W(x,t)$ is the concentration of lactic
acid. The reaction-diffusion system \eqref{GGsys} is a sound description of the
acid-mediated tumor growth mechanism. In what follows, we refer to \eqref{GGsys} as
the {\bf complete Gatenby--Gawlinski model} to distinguish it from a corresponding reduced
version to be introduced later.
The basics of such a modeling is rather clear. Firstly, healthy cells --denoted by $U$--
have a certain reproduction level (supposed logistic with rate $1$, for simplicity) and
are deteriorated by the acid, following the standard mass action law with kinetic constant
$d$. Secondly, the tumor cells $V$ have the capability of spreading at a rate that
depends on the quantity of healthy cells $U$, and they also reproduce according to a
logistic law, with a different rate denoted by $r$. A rough justification of the
dependence on $U$ in the coefficient of $\partial_x V$ is that tumor cells --possessing a
high-degree of invasiveness-- can hardly move when the density of healthy cells is high.
Specifically, the coefficient is null (no motion of cancerous tissue) if the healthy cells
are at carrying capacity. Finally the concentration $W$ of lactic acid undergoes
diffusion at constant rate $a$, and is increased proportionally to the unknown $V$,
with kinetic constant $b$, until it reaches the saturation level $W = V$. Let us stress
that the third unknown $W$ has no direct effect on the dynamics of the variable
$V$. The system is meaningful when the parameters $a,b,d,r$ are all positive.
Modifications of the original model have also been considered by many authors:
among others, we quote here \cite{McGiEtAl14} (generalized Gatenby--Gawlinski
model), \cite{ArauFassSalv18} (linear diffusion in the tumor variable),
\cite{HoldRodr15} (effect of chemotherapy), \cite{MartEtAl10} (stromal
interaction), \cite{StinSuruMera15} (distinction between intracellular and
extracellular proton dynamics). An interesting feature of the Gatenby--Gawlinski
model \eqref{GGsys} is the numerical evidence of existence of invasive
propagation fronts, i.e. special solutions describing the invasion of the cancer
cells into the healthy tissue. To our knowledge, no rigorous proof of the existence
of such front is available so far, except in some limiting parameter regimes.
To decrease the complexity of \eqref{GGsys}, we consider the reduced system
\begin{equation}\label{redGGsys}
\left\{\begin{aligned}
\partial_t U \,&=\, U \bigl\{f(U)- dV\bigr\}\,, \\
\partial_t V \,&=\, \partial_x \bigl\{f(U)\,\partial_x V\bigr\}+ r V f(V)\,,
\end{aligned}\right.
\end{equation}
obtainable as a formal limit in the regime $a\sim\textrm{const.}$ and $b\to\infty$,
that is replacing the last dynamical equation with the trivial constitutive identity $W=V$
(see \cite{FasaHerrRodr09, MascMoscSime21, MoscSime19}). Such a model intends to
describe the case in which the tumor cells act directly on the healthy tissue with
no additional specific intermediate (at the level of ODE, an analogous system has been
discussed in \cite{FassYang17}). We refer to \eqref{redGGsys} as the {\bf reduced
Gatenby--Gawlinski model}. It can be regarded as a simplified version of the system
proposed in \cite{McGiEtAl14}, obtained by rescaling the space and choosing
\begin{equation}\label{redGGgenGG}
a_2=d, \quad r_2=r, \quad a_1=d_1=d_2=0, \quad D=1, \quad c=b,
\end{equation}
where the parameters $a_1,a_2, d_1, d_2, r_2$ and $D$ are as in \cite{McGiEtAl14}.
Incidentally, let us observe that there are other possible reductions of the same
original complete model, which are obtained by considering different parameter
regimes and could also be worth investigating.
The diffusion coefficient $f(U) = 1-U$ in the $V$-equation of system~\eqref{redGGsys}
can be seen as an inherent defense process exerted by the healthy tissue in
response to the presence of the tumor. If the healthy cells are at their
carrying capacity, normalized to $1$, no invasion can occur; in contrast, tumor
starts growing whenever the density of healthy cells is lower than $1$, and in
absence of healthy tissue the tumor is free to permeate all the space.
Incidentally, we observe that $f(U)$ takes negative values when $U > 1$, so
that the diffusion equation for $V$ becomes ill-posed in such a regime.
In the subsequent traveling wave analysis, we restrict our attention to values
$U \in (0,1)$, so that $f(U) > 0$.
\subsection{Scalar reaction-diffusion equations with degenerate diffusion}
Propagation fronts attracted the interest of many researchers because they provide
the simplest mathematical framework describing the process of biological invasion.
Rigorous results concerning existence and asymptotic stability of traveling wave
solutions for scalar equations of the form
\begin{equation}\label{degFKPP}
\partial_t U \,=\, \partial_x \bigl\{\phi(U)\,\partial_x U\bigr\}+f(U)\,,
\end{equation}
with reaction term $f$ and nonlinear diffusion $\phi$, have been obtained under
various assumptions. When $\phi$ is a strictly positive constant, the diffusion
is linear and equation~\eqref{degFKPP} is semilinear. For $\phi$ dependent on $U$ and
attaining strictly positive values, the diffusion is nonlinear and non-degenerate. Here,
we are interested in the case in which the function $\phi$ is non-negative and null at
some specific points, usually $U=0$, the archetypal example being the {\it porous medium
equation} for which $\phi(s)\propto s^p$ for some $p>0$. Let us stress that considering a
function $\psi$ such that $\psi'=\phi$, equation \eqref{degFKPP} can be rewritten as
\begin{equation*}
\partial_t U \,=\, \partial_x^2 \psi(U)+f(U)\,,
\end{equation*}
corresponding to a porous medium equation with reaction. Existence of traveling wave
solutions has been widely explored in such a context, see \cite{Aron80, Engl85, GildKers05,
MalaMarc03, Newm80, SancMain94b, SancMain97, SancMain95, Sher10} for a single degeneration
point, and \cite{DrabTaka20, MalaMarc05, MalaMarc03, Mans10b} for multiple degenerations.
Different forms of the multiplier function $\phi$, e.g. depending on $\partial_x U$,
have also been considered (see \cite{AtkiReutRidl81,BengDepa18}).
In the scalar case, the typical existence statement --valid for linear, nonlinear
non-degenerate or degenerate diffusion-- can be rephrased as follows. Let the function
$f$ be of logistic type, i.e. it has two zeros (say $0$ and $1$) and is positive in
between. Then the scalar equation \eqref{degFKPP} supports traveling waves
$U(x,t)=\mathcal{U}(x-ct)$ satisfying the asymptotic conditions $\mathcal{U}(-\infty)=1$
and $\mathcal{U}(+\infty)=0$ if and only if $c\geq c_\ast$, for some strictly positive $c_\ast$.
Moreover, the solution to the initial value problem with Heaviside-like data, characterized
by a sharp jump from 0 to 1, converges in an appropriate sense to the traveling wave
connecting the states $0$ and $1$ and moving at critical speed $c_\ast$.
For traveling waves of linear diffusion equations, stability analysis is a
classical subject dating back to the pioneering papers by Fisher \cite{Fish37}
and Kolmogorov, Petrovskii and Piscounov \cite{KolmPetrPisc37}. Much less is
known, however, in the case of degenerate diffusion equations. One of the few
results is contained in \cite{LeyvPlaz20}, following the general method outlined
in \cite{MeyrRadeSier14} for general reaction-diffusion systems.
\subsection{Reaction-diffusion systems with cross-dependent self-diffusivities}
As expected, for systems, the situation is less clear.
First of all, it is necessary to agree on the terminology.
Let us consider, for simplicity, a $2\times2$ reaction-diffusion system of the form
\begin{equation}\label{2x2}
\left\{\begin{aligned}
\partial_t u \,&=\, \partial_x\bigl\{\phi_{11}(u,v)\partial_x u+\phi_{12}(u,v)\partial_x
v\bigr\}+F(u,v)\,, \\
\partial_t v \,&= \partial_x\bigl\{\phi_{21}(u,v)\partial_x u+\phi_{22}(u,v)\partial_x
v\bigr\}+ G(u,v)\,,
\end{aligned}\right.
\end{equation}
for some diffusivities $\phi_{ij}$ with $i,j\in\{1,2\}$ and reaction terms $F, G$.
Many examples for \eqref{2x2} with a significant applied perspective can be provided.
Among others, the celebrated {\it Keller--Segel chemotaxis model} --proposed as a
description for the motion of bacteria towards some optimal environment \cite{KellSege71}--
fits into the class choosing
\begin{equation*}
\phi_{11}(u,v)=a,\quad \phi_{12}(u,v)=0,\quad
\phi_{21}(u,v)=-b\,\chi(u),\quad \phi_{22}(u,v)=\mu(u),
\end{equation*}
and $F(u,v)=-\kappa(u)v$, $G(u,v)= 0$ for some parameters $a, b>0$ and functions $\kappa$,
$\mu$, $\chi$. The Keller--Segel system can be regarded as a prototype of ``exotaxis''
models because the gradient in the concentration of one species induces a flux of another
species.
A second example is \cite{ShigKawaTera79} --the progenitor of a long lineage--
where the terminology {\it cross-diffusion system} has been used to denote a
particular case of \eqref{2x2} characterized by the presence of the diffusion term
$\partial_x^2 \psi_i$ in place of $\partial_x(\phi_{i1}\partial_x u +\phi_{i2}\partial_x v)$
for $i=1,2$. In other words we assume that there exist $\psi_1, \psi_2$ such that
$\phi_{11} = \partial_u \psi_1$, $\phi_{12} = \partial_v\psi_1$, $\phi_{21} = \partial_u
\psi_2$, $\phi_{22}=\partial_v\psi_2$, which is not the case in general.
A simplified version of \eqref{2x2} is obtained by assuming the terms $\phi_{12}$ and
$\phi_{21}$ to be null, that is focusing on systems with {\it cross-dependent
self-diffusivities}:
\begin{equation}\label{2x2self}
\left\{\begin{aligned}
\partial_t u \,&=\, \partial_x\left\{\phi_{11}(u,v)\partial_x u\right\}+F(u,v)\,, \\
\partial_t v \,&= \partial_x\left\{\phi_{22}(u,v)\partial_x v\right\}+ G(u,v)\,.
\end{aligned}\right.
\end{equation}
Both species are submitted to self-diffusion with a diffusivity coefficient that, in
general, may depend on the other variable. The reduced Gatenby--Gawlinski model
\eqref{redGGsys} fits into \eqref{2x2self} with the choices
\begin{equation*}
\phi_{11}(u,v)=0,\quad \phi_{22}(u,v)=f(u),\quad F(u,v)=u \bigl\{f(u) - dv\bigr\},
\quad G(u,v)= r v f(v).
\end{equation*}
Coming back to the topic of invasion fronts in the case of reaction-diffusion systems, a
huge difference with respect to the scalar case arises already for linear self-diffusion
because the dimension of the phase-space for the traveling wave ODE is strictly larger
than two. Nonlinear non-degenerate self-diffusions make the analysis harder, but, in
principle, still manageable with an adapted strategy. In contrast, when the diffusion
operator degenerates at some values, the situation becomes more involved with a
pivotal role played by an appropriate {\it desingularization procedure}, which
will be explained below.
Focusing on the case of cross-dependent self-diffusivities, after the pioneering
contribution of Aronson \cite{Aron80} devoted to a predator-prey system, the
attention moved toward the model proposed by Kawasaki et al. \cite{KawaEtAl97},
which attempts to provide a detailed description of the patterns generate by
some colonies of bacteria, called {\it Bacillus subtilis} (see
\cite{BenjCoheLevi00} for a comprehensive review on cooperative
self-organization of micro-organisms). This model is composed by two coupled
evolution equations for the population density $b$ and the concentration of
nutrient $n$. Degenerate cross-dependent self-diffusion appears in the equation
for the bacteria $b$ and is proportional to the product of the two unknowns,
i.e. $D(n,b) \propto n\cdot b$. Investigations on existence of propagating
fronts in bacteria growth models --either from a purely analytical point of view
or from a numerical perspective-- have been performed in
\cite{FengZhou07,Mans10a,Mans17,SatnMainGardArmi01}. In particular, in
\cite{Mans17, SatnMainGardArmi01}, the existence result is very similar to the
one valid for the scalar case, including the existence of a traveling wave for
the critical speed.
Existence of propagation fronts for the complete Gatenby--Gawlinski model (and its
modifications) is cogently supported by partial results and numerical calculations,
see \cite{DaviEtAl18,FasaHerrRodr09,HoldRodrHerr14, McGiEtAl14, MoscSime19}. However,
rigorous mathematical results are very limited if not completely missing. Again, a
distinguished feature of the model is the presence of cross-dependent self-diffusion.
In contrast with the bacteria models, the cross-diffusion term $f(U)$ in the
$V$-equation is a monotone {\em decreasing} function of the variable $U$, and our
goal is to explore in detail the consequences of such kind of coupling, in the
particular example of the reduced Gatenby--Gawlinski model \eqref{redGGsys}.
\subsection{Statement of the main results}
A {\it traveling wave} for \eqref{redGGsys} is a solution of the form
\begin{equation*}
U(x,t) \,=\, \mathcal{U}(x-ct)\,, \quad V(x,t) \,=\, \mathcal{V}(x-ct)\,,
\end{equation*}
where the parameter $c \in \mathbb{R}$ is the propagation speed. If $\xi := x-ct$ denotes
the space variable in a comoving frame, the traveling wave profile formally
satisfies the ODE system
\begin{equation}\label{Ode1}
c\,\frac{{\rm d}\mathcal{U}}{{\rm d}\xi} + \mathcal{U}\bigl\{f(\mathcal{U}) - d\,\mathcal{V}\bigr\} \,=\, 0\,,\qquad
\frac{{\rm d}}{{\rm d}\xi}\left\{f(\mathcal{U})\frac{{\rm d}\mathcal{V}}{{\rm d}\xi}\right\} + c\,\frac{{\rm d}\mathcal{V}}{{\rm d}\xi}
+ r \mathcal{V} f(\mathcal{V}) \,=\, 0\,.
\end{equation}
A {\it propagation front} is a special type of traveling wave, enjoying the
asymptotic conditions
\begin{equation}\label{BC1}
\lim_{\xi\to\pm\infty} \bigl(\mathcal{U},\mathcal{V}\bigr)(\xi) \,=\, \bigl(\mathcal{U}_\pm,\mathcal{V}_\pm\bigr)\,.
\end{equation}
The asymptotic values $\bigl(\mathcal{U}_\pm,\mathcal{V}_\pm\bigr)$ are forced to be
constant equilibria to system \eqref{redGGsys}. While numerical evidence
of existence of traveling waves has been provided in \cite{MascMoscSime21, MoscSime19},
no rigorous result was obtained so far. In what follows, we will reconsider the above
definition of propagation front in order to incorporate
the presence of possible degeneracies.
When $d \neq 1$, system \eqref{redGGsys} has exactly four constant equilibria\thinspace :
the trivial state $(\bar U,\bar V) = (0,0)$, the healthy state $(1,0)$, the
cancerous state $(0,1)$ and the heterogeneous state $(1-d,1)$. Note that the
last equilibrium is positive, hence biologically significant, if and only if
$d < 1$. In the limiting case $d = 1$, the system has only three uniform
equilibria.
In this paper, we mainly concentrate on the case $d>1$, which seems most relevant in
cancerology (considering $d$ as a measure of aggressiveness of the tumor),
and we look for traveling wave solutions that describe the invasion of the
healthy state by the infected state. In other words, we choose as asymptotic values
\begin{equation}\label{BC1bis}
\bigl(\mathcal{U}_-,\mathcal{V}_-\bigr) \,=\, \bigl(0,1\bigr) \quad\textrm{and}\quad
\bigl(\mathcal{U}_+,\mathcal{V}_+\bigr) \,=\, \bigl(1,0\bigr)\,.
\end{equation}
This situation is referred to as {\bf homogeneous invasion}. We also study
more succinctly the regime $0<d<1$, in which homogeneous invasion is
not possible. In that case, we focus on {\bf heterogeneous invasion} which
corresponds to the asymptotic states
\begin{equation}\label{BC2}
\bigl(\mathcal{U}_-,\mathcal{V}_-\bigr) \,=\, \bigl(1-d,1\bigr)
\quad\textrm{and}\quad
\bigl(\mathcal{U}_+,\mathcal{V}_+\bigr) \,=\, \bigl(1,0\bigr)\,.
\end{equation}
The particular case $d = 1$ is non-generic, and will not be considered here.
It is important to keep in mind that the second equation in \eqref{redGGsys} is a {\it
degenerate parabolic equation}, see \cite{SancMain95}, in the sense that the coefficient
$f(U)$ in front of the leading order term $\partial_x^2 V$ vanishes when $U = 1$. For that
reason, it is not clear at all that system~\eqref{redGGsys} has global classical solutions,
and a similar caveat applies to the ODEs \eqref{Ode1} satisfied by the traveling waves.
Hence, we adopt here the following definition, which is adapted from \cite{HilhEtAl08} and based
on the notion of weak solution.
\begin{df}\label{df:front}
The triple $(\mathcal{U},\mathcal{V}; c)$ is a {\bf propagation front} for system \eqref{redGGsys}
connecting the asymptotic states $\bigl(\mathcal{U}_-,\mathcal{V}_-\bigr)$ and
$\bigl(\mathcal{U}_+,\mathcal{V}_+\bigr)$ if
\begin{itemize}
\item[\bf i)] $(\mathcal{U},\mathcal{V})\in C(\mathbb{R}\,;\,[0,1])\times C(\mathbb{R}\,;\,[0,1])$
and $f(\mathcal{U})\dfrac{{\rm d}\mathcal{V}}{{\rm d}\xi}\in L^2(\mathbb{R})$;
\item[\bf ii)] $(\mathcal{U},\mathcal{V})$ is a weak solution to \eqref{Ode1}, i.e. for all
$(\phi,\psi) \in C^1(\mathbb{R})\times C^1(\mathbb{R})$ with compact support
\begin{align}\label{frontdef1}
&\int_{\mathbb{R}} \mathcal{U}\left\{c\,\frac{{\rm d}\phi}{{\rm d}\xi} - \bigl[f(\mathcal{U})-d\,\mathcal{V}\bigr]
\phi\right\}{\rm d} \xi\,=\, 0\,,\\ \label{frontdef2}
&\int_{\mathbb{R}} \left\{\left[f(\mathcal{U})\frac{{\rm d}\mathcal{V}}{{\rm d}\xi} + c\,\mathcal{V}\,\right]
\frac{{\rm d}\psi}{{\rm d}\xi} - r \mathcal{V} f(\mathcal{V}) \psi \right\}{\rm d} \xi\,=\, 0\,;
\end{align}
\item[\bf iii)] the asymptotic conditions \eqref{BC1} are satisfied.
\end{itemize}
The couple $(\mathcal{U},\mathcal{V})$ is the {\bf profile of the front} and the value $c$ is
the {\bf speed of propagation}.
\end{df}
The main result of this paper is the following.
\begin{thm}\label{main1}
Assume that $d > 1$ and $r > 0$. For any $c > 0$, the reduced Gatenby--Gawlinski
system \eqref{redGGsys} has a propagation front $\bigl(\mathcal{U},\mathcal{V};c\bigr)$ connecting
$(0,1)$ with $(1,0)$. This solution is unique up to translations and both components
$\mathcal{U}, \mathcal{V}$ are strictly monotone functions of $\xi = x-ct$.
\end{thm}
The proof also provides detailed information on the behavior of the front profile as
$\xi \to \pm\infty$. In particular, we can choose a translate of the wave such that
\begin{equation}\label{AsymUV1}
\mathcal{U}(\xi) \,=\, \alpha e^{\mu \xi} + \mathcal{O}\bigl(e^{(\mu+\eta)\xi}\bigr)\,,
\qquad \mathcal{V}(\xi) \,=\, 1 - e^{\lambda \xi} + \mathcal{O}\bigl(e^{(\lambda+\eta)
\xi}\bigr)\,, \qquad \hbox{as}\quad \xi \to -\infty\,,
\end{equation}
for some $\alpha > 0$, where
\begin{equation}\label{lamudef}
\lambda \,=\, \frac12\bigl(-c + \sqrt{c^2 + 4r}\bigr) \,>\, 0\,,
\qquad \mu \,=\, \frac{d-1}{c} \,>\, 0\,, \qquad
\eta \,=\, \min(\lambda,\mu)\,.
\end{equation}
Moreover, there exists $\beta > 0$ such that
\begin{equation}\label{AsymUV2}
\mathcal{U}(\xi) \,=\, 1 - \beta e^{-\gamma\xi} + \mathcal{O}\bigl(e^{-2\gamma\xi}\bigr)\,,
\qquad \mathcal{V}(\xi) \,=\, \beta\,\frac{r+1}{d}\,e^{-\gamma\xi}
+ \mathcal{O}\bigl(e^{-2\gamma \xi}\bigr)\,,
\end{equation}
as $\xi \to +\infty$, where $\gamma = r/c$.
\begin{figure}
\caption{{\small The profile $(\mathcal{U}
\label{fig1}
\end{figure}
Most remarkably, Theorem~\ref{main1} shows that there exists {\bf no minimal speed} for
the propagation fronts of system \eqref{redGGsys}. This is in sharp contrast with what
happens for scalar equations involving a degenerate diffusion, see
\cite{SancMain94b,SancMain97} and also \cite{SatnMainGardArmi01} (for the Kawasaki
system). To elaborate on that, we consider a further formal reduction of system
\eqref{redGGsys}, which seems reasonable at least for solutions that evolve slowly in
time. In view of the first equation in \eqref{redGGsys}, one can expect that the first
component $U$ should stay close to $1-dV$ if $dV \le 1$ and to zero if $dV > 1$. Assuming
this to be exactly true, we obtain a scalar evolution equation for the second component
$V$\thinspace :
\begin{equation}\label{GGscalar}
\partial_t V \,=\, \partial_x \left\{\phi(V)\partial_x V\right\}+ r V f(V)\,,
\qquad \hbox{where}\quad \phi(V) \,:=\, \min(dV,1)\,.
\end{equation}
Strictly speaking, the results of \cite{SancMain97, MalaMarc05} do not apply to
\eqref{GGscalar} because the diffusion coefficient $\phi$ is only a Lipschitz
function of $V$. Disregarding that technical issue, we expect nevertheless that
equation \eqref{GGscalar} has monotone front solutions satisfying
$\mathcal{V}(-\infty) = 1$, $\mathcal{V}(+\infty) = 0$ if and only if $c \ge c_*$, for some
minimal speed $c_* = c_*(d,r) > 0$. Moreover, when $c = c_*$, the front profile
is ``sharp'' in the sense that there exists $\bar\xi \in \mathbb{R}$ such that
$\mathcal{V}(\xi) = 0$ for all $\xi \ge \bar\xi$. Quite surprisingly,
Theorem~\ref{main1} shows that the PDE system \eqref{redGGsys} behaves
differently\thinspace : propagation fronts exist for all positive speeds $c > 0$, no
matter how small, and all front profiles are smooth and strictly monotone. Sharp
fronts, which are typical for scalar equations with degenerate diffusion, do not
exist in system \eqref{redGGsys}.
Of course, this discrepancy means that the formal reduction leading to \eqref{GGscalar}
is not justified. In fact, if $(\mathcal{U},\mathcal{V})$ is the front profile given by
Theorem~\ref{main1}, for some values of the parameters $d,r,c$, we can introduce
the {\em effective diffusion coefficient} $\phi : (0,1) \to (0,1)$ defined by
\begin{equation}\label{Deff}
1 - \mathcal{U}(\xi) \,=\, \phi\bigl(\mathcal{V}(\xi)\bigr)\,, \qquad \xi \in \mathbb{R}\,.
\end{equation}
By construction, the second component $\mathcal{V}$ of the front profile is a
traveling wave solution of the scalar equation \eqref{GGscalar} with
$\phi$ given by \eqref{Deff}. In particular we must have
$c \ge c_*(\phi,r)$, where $c_*$ is the minimal speed for the scalar
equation. Numerical calculations shows that the shape of the effective
diffusion coefficient $\phi$ depends strongly on the values of the
parameters $d,r,c$, and it often very different from the naive guess
$\phi(V) = \min(dV,1)$. This is especially true when $c$ is small, in
which case $\phi(V)$ is found to be extremely flat near the origin $V = 0$,
see the discussion at the end of Section~\ref{sec3}.
Going back to \eqref{redGGsys}, in the case where $0 < d < 1$, the system has an additional,
biologically significant, equilibrium $(\bar U,\bar V) = (1-d,1)$ in which healthy and cancerous
cells coexist. In that case, it is natural to consider traveling waves that connect the
coexistence state to the healthy state given by \eqref{BC2}. We have the following
analogue of Theorem~\ref{main1}.
\begin{thm}\label{main2}
Assume that $0 < d < 1$ and $r > 0$. For any $c > 0$, the reduced Gatenby--Gawlinski
system \eqref{redGGsys} has a propagation front $\bigl(\mathcal{U},\mathcal{V};c\bigr)$ connecting
$(1-d,1)$ with $(1,0)$. This solution is unique up to translations and both
components $\mathcal{U}$ and $\mathcal{V}$ are strictly monotone. Moreover, there is no
propagation front connecting $(0,1)$ with $(1,0)$ in that case.
\end{thm}
\begin{figure}
\caption{{\small The profile $(\mathcal{U}
\label{fig2}
\end{figure}
The rest of this article is organized as follows. Section \ref{sec2} is mainly
devoted to the proof of Theorem~\ref{main1}. Our starting point is the
desingularization of the ODE system \eqref{Ode1}, using a standard procedure
that was already known for scalar equations with degenerate diffusion.
Propagation fronts are then constructed as heteroclinic connections between two
equilibria of the desingularized system. The unstable manifold of the infected
state is two-dimensional in that setting, which forces us to introduce an additional
shooting parameter, and an important part of our analysis relies on monotonicity
properties with respect to that shooting parameter. The proof of Theorem
\ref{main2} goes along the same lines, and is briefly presented in
Section~\ref{subsec27}. In Section~\ref{sec3}, we explore the limiting regime
where $c\to 0$, and we derive an asymptotic expansion of the front profile that
is remarkably accurate even at moderately small speeds. Finally, we draw some
conclusions in Section~\ref{sec4} and we outline a few perspectives.
\subsection*{Acknowledgments.} The research of the first named author
is partially supported by the grant ISDEEC ANR-16-CE40-0013 of the French
Ministry of Higher Education, Research and Innovation. This work benefited
from mutual invitations, on the occasion of which the hospitality of
Universit\'e Grenoble Alpes and Sapienza, Universit\`a di Roma is gratefully
acknowledged.
\section{Existence of propagation fronts}\label{sec2}
This section is devoted to the proofs of Theorem~\ref{main1} and \ref{main2}. We assume
that the reader is familiar with center manifold theory for ODEs and normal form theory.
All necessary material can be found in classical monographs such as \cite{CLW,GH,HI}, to
which we shall refer when needed.
In what follows, we fix the parameters $d > 0$ and $r > 0$ in system~\eqref{Ode1}. All
quantities that appear in the proof depend on $d,r$, but for notational simplicity this
dependence will not be indicated explicitly.
\subsection{Preliminary results}
\label{subsec21a}
The underlying ODE system of \eqref{redGGsys} is
\begin{equation}\label{uniform}
\frac{{\rm d} U}{{\rm d} t}=\, F(U,V;d)\,:=\,U\bigl(f(U)- d V\bigr)\,,\quad
\frac{{\rm d} V}{{\rm d} t}\,=\, G(U,V;r)\,:=\, r V f(V)\,.
\end{equation}
Regardless of the biological meaning of the variables, uniform
equilibria of \eqref{redGGsys} are
\begin{equation*}
(\bar U,\bar V)=(0,0),\qquad (\bar U,\bar V)=(1,0),\qquad (\bar U,\bar V)=(0,1),
\qquad (\bar U,\bar V)=(1-d,1)\,.
\end{equation*}
Computing the partial derivatives of $F$ and $G$, we determine the
linearized equation of \eqref{uniform} at $(\bar U,\bar V)$, which is
\begin{equation*}
\frac{{\rm d}}{{\rm d} t}\begin{pmatrix} u \\ v\end{pmatrix}
=\mathbf{A}\begin{pmatrix} u \\ v\end{pmatrix}
\quad\textrm{where}\quad
\mathbf{A}:=\begin{pmatrix} 1-2\bar U-d\bar V & -d\bar U \\ 0 &
r(1-2\bar V)\end{pmatrix}\,.
\end{equation*}
Hence, for the uniform equilibria, the following properties hold\thinspace :
\begin{itemize}
\item[\bf i)] $(0,0)$ is always an unstable node (eigenvalues $1$ and $r$);
\item[\bf ii)] $(1,0)$ is always a saddle (eigenvalues $-1$ and $r$);
\item[\bf iii)] $(0,1)$ is a saddle if $d<1$ and a stable node if $d>1$
(eigenvalues $1-d$ and $-r$);
\item[\bf iv)] $(1-d,1)$ is a stable node if $d<1$ and a saddle if $d>1$
(eigenvalues $d-1$ and $-r$).
\end{itemize}
Note the stability exchange between $(1-d,1)$ and $(0,1)$ when passing
the threshold $d=1$. In what follows, we look for propagation fronts with
asymptotic states \eqref{BC1bis} if $d > 1$ and \eqref{BC2} if $d < 1$.
The non-generic case $d = 1$ will not be considered.
\begin{lem}\label{lem:positivec}
If $(\mathcal{U},\mathcal{V};c)$ is a propagation front in the sense of Definition~\ref{df:front},
then $\mathcal{V} f(\mathcal{V}) \in L^1(\mathbb{R})$ and
\begin{equation}\label{cformula}
c \,=\, r\int_{\mathbb{R}} \mathcal{V}(\xi) f(\mathcal{V}(\xi)) \,{\rm d}\xi \,>\, 0\,.
\end{equation}
\end{lem}
\begin{proof}
Let $\chi : \mathbb{R} \to \mathbb{R}$ be a smooth non-decreasing function satisfying
$\chi(x) = -1/2$ for $x \le -1$ and $\chi(x) = 1/2$ for $x \ge 1$.
Given any $L > 1$, we consider the relation \eqref{frontdef2} in
Definition~\ref{df:front}, with $\psi(\xi) = \psi_L(\xi) := \chi(\xi+L) - \chi(\xi-L)$.
Note that $\psi$ is a smooth approximation of the characteristic function
of the interval $[-L,L]$. Since $\mathcal{V}$ is a continuous function having finite
limits at infinity, we find
\[
c \int_\mathbb{R} \mathcal{V}\,\psi_L'\,{\rm d}\xi ~\xrightarrow[L\to\infty]{}~
c \bigl(\mathcal{V}(-\infty) - \mathcal{V}(+\infty)\bigr) \,=\, c\,.
\]
Moreover, using H\"older's inequality, we can bound
\[
\biggl|\int_\mathbb{R} f(\mathcal{U})\mathcal{V}' \psi_L'\,{\rm d}\xi\biggr| \,\le\, \|\chi'\|_{L^2}
\left\{\biggl(\int_{-L-1}^{-L+1} \bigl|f(\mathcal{U})\mathcal{V}'\bigr|^2\,{\rm d}\xi\biggr)^{1/2}
+ \biggl(\int_{L-1}^{L+1} \bigl|f(\mathcal{U})\mathcal{V}'\bigr|^2\,{\rm d}\xi\biggr)^{1/2}
\right\}\,,
\]
and the right-hand side converges to zero as $L \to +\infty$ because
$f(\mathcal{U})\mathcal{V}' \in L^2(\mathbb{R})$ by assumption. So we deduce from \eqref{frontdef2}
that
\[
r\int_\mathbb{R} \mathcal{V} f(\mathcal{V})\psi_L \,{\rm d} \xi ~\xrightarrow[L\to\infty]{}~c\,,
\]
which gives the desired result since $\mathcal{V} f(\mathcal{V}) \ge 0$ and $\psi_L$ increases
to $1$ as $L \to +\infty$.
\end{proof}
\begin{lem}\label{lem:sharp}
If $(\mathcal{U},\mathcal{V};c)$ is a propagation front in the sense of Definition~\ref{df:front},
there exists a unique point $\bar\xi \in \mathbb{R} \cup \{+\infty\}$ such that\\[1mm]
1) $\mathcal{U},\mathcal{V} \in C^\infty((-\infty,\bar\xi))$ and $0 < \mathcal{U}(\xi),\mathcal{V}(\xi) < 1$
for $\xi < \bar\xi$;\\[1mm]
2) If $\bar\xi < \infty$, then $\mathcal{U}(\xi) = 1$ and $\mathcal{V}(\xi) = 0$ for all
$\xi \ge \bar\xi$.
\end{lem}
In other words, the propagation front $(\mathcal{U},\mathcal{V};c)$ is {\bf smooth} if
$\bar\xi = +\infty$, and {\bf sharp} if $\bar\xi < +\infty$. In fact, we shall eventually
prove that the latter case cannot occur for system~\eqref{Ode1}, but at the moment we have
to consider both possibilities.
\begin{proof}
Since $\mathcal{U},\mathcal{V}$ are continuous functions and $c > 0$ by Lemma~\ref{lem:positivec}, we
deduce from \eqref{frontdef1} that $\mathcal{U} \in C^1(\mathbb{R})$ and $\mathcal{U}$ is a classical solution of
the first ODE in \eqref{Ode1}. In particular $\mathcal{U}$ cannot vanish without being identically
zero, which would contradict the assumption that $\mathcal{U}_+ = 1$, hence $\mathcal{U}(\xi) > 0$ for all
$\xi \in \mathbb{R}$. On the other hand, we know from \eqref{BC1} that $\mathcal{U}(\xi) < 1$ when $\xi$
is large and negative. Thus either $\mathcal{U}(\xi) < 1$ for all $\xi \in \mathbb{R}$, in which case we
set $\bar\xi = +\infty$, or there exists a (unique) point $\bar\xi \in \mathbb{R}$ such that
$\mathcal{U}(\bar\xi) = 1$ and $\mathcal{U}(\xi) < 1$ for all $\xi < \bar \xi$.
According to \eqref{frontdef2}, on the interval $I := (-\infty,\bar \xi)$ the function
$\mathcal{V}$ is a weak solution of an elliptic ODE, so that $\mathcal{V}$ is of class $C^2$ and satisfies
the second ODE in \eqref{Ode1} in the classical sense. In fact, using \eqref{Ode1} and a
bootstrap argument, it is easy to verify that $\mathcal{U},\mathcal{V} \in C^\infty(I)$. Moreover, since
$0 \le \mathcal{V} \le 1$ and since the nonlinear term $\mathcal{V} f(\mathcal{V})$ vanishes when $\mathcal{V} = 0$ and
$\mathcal{V} = 1$, it is clear that $\mathcal{V}$ cannot vanish on $I$ without being identically zero,
which would contradict the assumption that $\mathcal{V}_- = 1$. Similarly, if $1 - \mathcal{V}$ vanishes
somewhere on $I$, then $\mathcal{V} \equiv 1$ on $I$; if $\bar\xi = +\infty$, this contradicts the
assumption that $\mathcal{V}_+ = 0$, and if $\bar\xi < +\infty$ this implies that
$\mathcal{U}'(\bar\xi) = d/c > 0$, which is of course impossible since $0 \le \mathcal{U} \le 1$. The
proof of 1) is thus complete.
It remains to prove 2), assuming of course that $\bar\xi < +\infty$. Since
$\mathcal{V}(\xi) \ge 0$ by assumption, the first ODE in \eqref{Ode1} shows that
$c\,\mathcal{U}'(\xi) = \mathcal{U}(\xi)\bigl(\mathcal{U}(\xi) + d\mathcal{V}(\xi) - 1\bigr) \ge \mathcal{U}(\xi)\bigl(\mathcal{U}(\xi)
- 1\bigr)$, with equality if and only if $\mathcal{V}(\xi) = 0$. Since $\mathcal{U}(\bar\xi) = 1$ and
$\mathcal{U}(\xi) \le 1$ for all $\xi \ge \bar\xi$, the only possibility is that $\mathcal{U}(\xi) = 1$
and $\mathcal{V}(\xi) = 0$ for all $\xi\ge\bar\xi$. This concludes the proof.
\end{proof}
\subsection{Desingularization of the ODE system}
\label{subsec21}
Here, we concentrate on the regime $d>1$ and we look for propagation fronts with
asymptotic states \eqref{BC1bis}. We know from Lemma~\ref{lem:positivec} that $c>0$, and
from Lemma~\ref{lem:sharp} that the profiles $\bigl(\mathcal{U},\mathcal{V}\bigr)$ satisfy \eqref{Ode1} in
the classical sense on the interval $I = (-\infty,\bar\xi)$ for some
$\bar\xi \in \mathbb{R} \cup\{+\infty\}$. The ODE system \eqref{Ode1} degenerates in the limit
where $\xi \to \bar\xi$, which complicates the analysis. Fortunately, as in scalar
equations \cite{Engl85}, it is possible to desingularize \eqref{Ode1} using a relatively
simple change of variables.
Given a solution $\bigl(\mathcal{U},\mathcal{V}\bigr) : I \to (0,1)^2$ of \eqref{Ode1}
satisfying \eqref{BC1}, we define a new independent variable $y = \Phi(\xi)$
by setting
\begin{equation}\label{ydef}
\frac{{\rm d} y}{{\rm d} \xi} \,\equiv\, \Phi'(\xi) \,=\, \frac{1}{1 - \mathcal{U}(\xi)}\,,
\qquad \hbox{for all~} \xi \in I = (-\infty,\bar\xi)\,.
\end{equation}
Since $\mathcal{U} \in C^1(\mathbb{R})$ and $U(\xi) \to 1$ as $\xi \to \bar\xi$, it is clear that
\[
\int_{-\infty}^0 \frac{1}{1 - \mathcal{U}(\xi)}\,{\rm d}\xi \,=\, +\infty
\qquad\hbox{and}\quad
\int_0^{\bar\xi} \frac{1}{1 - \mathcal{U}(\xi)}\,{\rm d}\xi \,=\, +\infty\,,
\]
no matter whether $\bar\xi < +\infty$ or $\bar\xi = +\infty$. This shows that
$\Phi :I \to \mathbb{R}$ is a smooth diffeomorphism, so that we can introduce the new
dependent variables $(u,v)$ defined by
\begin{equation}\label{uvdef}
u(y) \,=\, \mathcal{U}\bigl(\Phi^{-1}(y)\bigr)\,, \quad
v(y) \,=\, \mathcal{V}\bigl(\Phi^{-1}(y)\bigr)\,, \qquad y \in \mathbb{R}\,.
\end{equation}
Using \eqref{ydef}, \eqref{uvdef}, it is straightforward to verify that the functions
$u,v$ are solution of the desingularized system
\begin{equation}\label{Ode2}
\left\{\begin{aligned}
c\,\frac{{\rm d} u}{{\rm d} y} + u(1-u)(1-u - d v) \,&=\, 0\,,\\
\frac{{\rm d}^2 v}{{\rm d} y^2} + c\,\frac{{\rm d} v}{{\rm d} y} + r v(1-u)(1-v) \,&=\, 0\,,
\end{aligned}\right.
\end{equation}
which is considered on the whole real line. The boundary conditions are unchanged:
\begin{equation}\label{BC3}
\lim_{y \to -\infty}\bigl(u(y),v(y)\bigr) \,=\, (0,1)\,,
\qquad
\lim_{y \to +\infty}\bigl(u(y),v(y)\bigr) \,=\, (1,0)\,.
\end{equation}
It is important to observe that the desingularized system \eqref{Ode2} has many more
equilibria than the original system \eqref{Ode1}. Indeed, in addition to the trivial
state $(u,v) = (0,0)$ and the infected stated $(u,v) = (0,1)$, system \eqref{Ode2} has a
continuous family of equilibria of the form $(u,v) = (1,v_\infty)$ for arbitrary
$v_\infty \in \mathbb{R}$. Except for the healthy state $(u,v) = (1,0)$, those equilibria are an
artifact of the change of variables \eqref{ydef} and do not correspond to physically
meaningful situations.
If we introduce the additional variable $w = {{\rm d} v}/{{\rm d} y}$, we obtain
from \eqref{Ode2} the first-order system
\begin{equation}\label{Ode3}
\left\{\begin{aligned}
c\frac{{\rm d} u}{{\rm d} y} \,&=\, -u(1-u)(1-u - d v)\,, \\
\frac{{\rm d} v}{{\rm d} y}\,&=\, w\,, \\
\frac{{\rm d} w}{{\rm d} y} \,&=\, -c w - rv(1-u)(1-v)\,,
\end{aligned}\right.
\end{equation}
which is the starting point of our analysis. In the following sections, we
consider solutions of \eqref{Ode3} that lie in the region $\mathcal{D} \subset \mathbb{R}^3$
defined by
\begin{equation}\label{Ddef}
\mathcal{D} \,=\, \bigl\{(u,v,w) \in \mathbb{R}^3\,\big|\, 0 < u < 1\,,~
0 < v < 1\,,~ w < 0\bigr\}\,.
\end{equation}
Indeed, the constraints $0 < u,v < 1$ were established in Lemma~\ref{lem:sharp},
and we shall see below that all front profiles also satisfy $w < 0$.
\subsection{The unstable manifold of the infected state}
\label{subsec22}
The linearization of system \eqref{Ode3} at the infected state $S_- = (0,1,0)$ is
\begin{equation}\label{linS-}
c\frac{{\rm d} u}{{\rm d} y} \,=\, (d-1)\,u\,, \quad \frac{{\rm d} z}{{\rm d} y} \,=\, - w\,,
\quad \frac{{\rm d} w}{{\rm d} y} \,=\, -rz-cw\,,
\end{equation}
where $z = 1 -v$. The equilibrium $S_-$ is thus hyperbolic, with two
positive eigenvalues $\lambda,\mu$ given by \eqref{lamudef}, and one
negative eigenvalue $\zeta = -\frac12\bigl(c + \sqrt{c^2 + 4r}\bigr)$.
In view of \eqref{BC3}, we are are interested in solutions that lie on
the two-dimensional unstable manifold of $S_-$. It is a
straightforward task to compute an asymptotic expansion of all such
solutions in a neighborhood of $S_-$, see e.g. \cite[Chapter~3]{GH}.
Keeping only the solutions that belong to the region $\mathcal{D}$ near $S_-$,
we obtain the following representation:
\begin{lem}\label{lem:unstab} Fix $c > 0$. For any $\alpha > 0$,
the ODE system \eqref{Ode3} has a unique solution such that
\begin{align}\nonumber
u(y) \,&=\, \alpha\,e^{\mu y} + \mathcal{O}\Bigl(e^{(\mu + \eta)y}
\Bigr)\,, \\ \label{asym1}
v(y) \,&=\, 1 - e^{\lambda y} + \mathcal{O}\Bigl(e^{(\lambda + \eta)y}\Bigr)\,, \\
\nonumber
w(y) \,&=\, - \lambda\,e^{\lambda y} + \mathcal{O}\Bigl(e^{(\lambda + \eta)y}\Bigr)\,,
\end{align}
as $y \to -\infty$, where $\lambda,\mu$ are given by \eqref{lamudef}
and $\eta = \min(\lambda,\mu) > 0$.
\end{lem}
\begin{rem}\label{rem:allsol}
Up to translations in the variable $y \in \mathbb{R}$, Lemma~\ref{lem:unstab}
describes all solutions of \eqref{Ode3} that converge to $S_-$ as
$y \to -\infty$ and belong to the region $\mathcal{D}$ for sufficiently large
$y < 0$. To prove Theorem~\ref{main1}, our strategy is to study the
behavior of those solutions as a function of the {\em shooting parameter}
$\alpha > 0$ and the {\em speed parameter} $c > 0$. When needed,
we denote by $(u_{\alpha,c},v_{\alpha,c},w_{\alpha,c})$ the unique solution
of \eqref{Ode3} satisfying \eqref{asym1}. Among other properties,
we shall use the fact that, for any $y_0 \in \mathbb{R}$, the solution
$(u_{\alpha,c}(y),v_{\alpha,c}(y),w_{\alpha,c}(y))$ depends continuously on the
shooting parameter $\alpha$, uniformly in $y \in (-\infty,y_0]$.
\end{rem}
The solution of \eqref{Ode3} satisfying \eqref{asym1} is not
necessarily globally defined. The following result clarifies
under which condition the solution is global and stays in the
region \eqref{Ddef} for all $y \in \mathbb{R}$.
\begin{lem}\label{lem:invariance}
If the solution $(u_{\alpha,c},v_{\alpha,c},w_{\alpha,c})$ is defined on
some interval $J = (-\infty,y_0)$ and satisfies
$v_{\alpha,c}(y) > 0$ for all $y \in J$, then $(u_{\alpha,c}(y),
v_{\alpha,c}(y),w_{\alpha,c}(y)) \in \mathcal{D}$ for all $y \in J$.
\end{lem}
\begin{proof}
We denote $(u,v,w) = (u_{\alpha,c},v_{\alpha,c},w_{\alpha,c})$.
Since the right-hand side of the first equation in \eqref{Ode3} vanishes
when $u = 0$ and $u = 1$, it is clear that $0 < u(y) < 1$ for all
$y \in J$. Next, assuming that $v(y)$ stays positive, we claim that
$w(y) < 0$ for all $y \in J$. Indeed, if this is not the case, we
can find $y_1 < y_0$ such that $w(y_1) = 0$ and $w(y) < 0$ for all
$y \in (-\infty,y_1)$. In particular, we have $0 < v(y) < 1$ for
all $y \in (-\infty,y_1]$, and the last equation in \eqref{Ode3}
shows that $w'(y_1) = -r(1-u(y_1))v(y_1)(1-v(y_1)) < 0$, which
gives a contradiction. So $w(y) < 0$ for all $y \in J$, which
implies that $0 < v(y) < 1$ for all $y \in J$.
\end{proof}
For any $\alpha > 0$ and $c > 0$, we now define
\begin{equation}\label{Tdef}
T(\alpha,c) \,=\, \sup\bigl\{y_0 \in \mathbb{R}\,\big|\,
v_{\alpha,c}(y) > 0 \hbox{ for all } y < y_0\bigr\} \,\in\,
(-\infty,+\infty]\,.
\end{equation}
According to Lemma~\ref{lem:invariance}, there are just two possibilities\thinspace :
\begin{itemize}
\item Either $T(\alpha,c) < +\infty$, in which case
$v_{\alpha,c}(T(\alpha,c)) = 0$ and $w_{\alpha,c}(T(\alpha,c)) < 0$,
so that $v_{\alpha,c}(y)$ becomes negative for some $y > T(\alpha,c)$.
The corresponding value of the shooting parameter $\alpha$ must
therefore be disregarded.
\item Or $T(\alpha,c) = +\infty$, in which case the solution
$(u_{\alpha,c},v_{\alpha,c},w_{\alpha,c})$ is global and stays in the
region $\mathcal{D}$ for all $y \in \mathbb{R}$. These are the solutions among
which we want to find the traveling wave profiles satisfying
\eqref{BC3}.
\end{itemize}
\subsection{Monotonicity with respect to the shooting parameter}
\label{subsec23}
A crucial observation is that the solutions of \eqref{Ode3} on
the unstable manifold of $S_-$ are monotone functions of the
shooting parameter $\alpha$. The precise statement is the
following\thinspace :
\begin{lem}\label{lem:monotone} Fix $c > 0$. If $\alpha_2 > \alpha_1 > 0$,
then $T(\alpha_2,c) \ge T(\alpha_1,c)$ and the solutions of
\eqref{Ode3} defined by \eqref{asym1} satisfy
\begin{equation}\label{comp1}
u_{\alpha_2,c}(y) \,>\, u_{\alpha_1,c}(y)\,, \quad
v_{\alpha_2,c}(y) \,>\, v_{\alpha_1,c}(y)\,,
\end{equation}
for all $y \in (-\infty,T(\alpha_1,c))$.
\end{lem}
\begin{proof}
Fix $\alpha_2 > \alpha_1 > 0$. In a first step, we show that
inequalities \eqref{comp1} hold for all sufficiently large $y < 0$.
From \eqref{asym1} we already know that $u_{\alpha_2,c}(y) - u_{\alpha_1,c}(y)
\approx (\alpha_2-\alpha_1)\,e^{\mu y}$ as $y \to -\infty$, which proves
the first inequality in \eqref{comp1} in the asymptotic regime.
To establish the second inequality, we need a higher order expansion
of the solutions on the unstable manifold of $S_-$, which can be obtained
as follows. For $i = 1,2$, we denote $u_i = u_{\alpha_i,c}$, $v_i =
v_{\alpha_i,c}$, and we introduce the functions $\omega_i$ defined by
$\omega_i(y) = e^{-\lambda y}(1 - v_i(y))$, for $y < 0$ sufficiently
large. A direct calculation shows that
\begin{equation*}
\omega_i'' + \delta \omega_i' + r \omega_i F\bigl(u_i,e^{\lambda y}\omega_i\bigr)
\,=\, 0\,,\qquad i = 1,2\,,
\end{equation*}
where $\delta = \sqrt{c^2 + 4r}$ and $F(u,\tilde v) = u + (1-u)\tilde v$. In addition,
according to \eqref{asym1}, we have $\omega_i(y) \to 1$ and $\omega_i'(y) \to 0$
as $y \to -\infty$. We now consider the difference $\omega = \omega_1 - \omega_2$,
which satisfies the inhomogeneous equation
\begin{equation}\label{omeq}
\omega'' + \delta \omega' + r\omega G \,=\, rf\,,
\end{equation}
where $G = G(y) := u_2 + (1-u_2)e^{\lambda y}(\omega_1+\omega_2)$ and $f = f(y) :=
\omega_1(u_2-u_1)(1-e^{\lambda y}\omega_1)$. Integrating \eqref{omeq} and using the fact
the $\omega(y) \to 0$ and $\omega'(y) \to 0$ as $y \to -\infty$, we obtain the
integral equation
\begin{equation}\label{omeqint}
\omega(y) \,=\, \frac{r}{\delta}\int_{-\infty}^y \Bigl(1 - e^{-\delta(y-z)}\Bigr)
\Bigl(f(z) - \omega(z)G(z)\Bigr) \,{\rm d} z\,,
\end{equation}
which can be used to compute iteratively an asymptotic expansion of $\omega(y)$ as
$y \to -\infty$. Since $G(y) = \mathcal{O}(e^{\eta y})$ as $y \to -\infty$, where $\eta =
\min(\lambda,\mu) > 0$, the leading order term is simply obtained by setting
$\omega = 0$ in the right-hand side of \eqref{omeqint}.
If we observe that
\begin{equation*}
f(y) \,=\, \omega_1(y) \bigl(u_2(y) - u_1(y)\bigr) \Bigl(1 - e^{\lambda y}
\omega_1(y)\Bigr) \,=\, (\alpha_2-\alpha_1)e^{\mu y} + \mathcal{O}\Bigl(e^{(\mu + \eta)y}\Bigr)\,,
\end{equation*}
we thus find
\begin{equation}\label{omexp}
\omega(y) \,\equiv\, \omega_1(y) - \omega_2(y) \,=\,
\frac{r(\alpha_2 - \alpha_1)}{\mu(\mu+\delta)}\,e^{\mu y}
+ \mathcal{O}\Bigl(e^{(\mu + \eta)y}\Bigr)\,, \qquad \hbox{as }y \to -\infty\,.
\end{equation}
Recalling that $\alpha_2 > \alpha_1$, we conclude that $\omega_1(y) > \omega_2(y)$ when
$y < 0$ is sufficiently large, which means that the second inequality in \eqref{comp1}
holds in the asymptotic regime. It also follows from the representation formula
\eqref{omeqint} that $\omega'(y) > 0$ when $y < 0$ is sufficiently large, and this in turn
implies that $v_2'(y) > v_1'(y)$ in that region. Summarizing, we have shown that there
exists $y_1 \in \mathbb{R}$ such that inequalities \eqref{comp1} hold for all
$y \in (-\infty,y_1]$. Moreover $v_{\alpha_2,c}'(y_1) > v_{\alpha_1,c}'(y_1)$.
In a second step, we prove that $T(\alpha_2,c) \ge T(\alpha_1,c)$ and that inequalities
\eqref{comp1} hold for all $y \in (-\infty, T(\alpha_1,c))$. Indeed, if this is not the
case, there exists $y_2 < \min\{T(\alpha_1,c),T(\alpha_2,c)\}$ such that both inequalities
in \eqref{comp1} hold on the interval $(y_1,y_2)$, but at least one becomes an equality at
$y = y_2$. Our strategy is to show that this is impossible. Denoting as before
$u_i = u_{\alpha_i,c}$ and $v_i = v_{\alpha_i,c}$ for $i = 1,2$, we observe that
\begin{equation*}
v_i'' + c v_i' + \phi_i v_i \,=\, 0\,, \qquad
\textrm{where}\quad \phi_i \,=\, r(1-u_i)(1-v_i)\,.
\end{equation*}
As $0 < u_1(y) < u_2(y) < 1$ and $0 < v_1(y) < v_2(y) < 1$ for all
$y \in [y_1,y_2)$, it is clear that $\phi_1(y) > \phi_2(y) > 0$
on that interval. We consider the ratio $\rho(y) = v_2(y)/v_1(y)$,
which satisfies
\begin{equation}\label{rhoeq}
\rho''(y) + \left(c + \frac{2v_1'(y)}{v_1(y)}\right)\rho'(y)
- \bigl(\phi_1(y)-\phi_2(y)\bigr)\rho(y) \,=\, 0\,, \qquad y \in (y_1,y_2)\,.
\end{equation}
We know that $\rho(y_1) > 1$ and $\rho'(y_1) > 0$, because the point $y_1$ was chosen so
that $v_2(y_1) > v_1(y_1) > 0$ and $v_1'(y_1) < v_2'(y_1) < 0$. On the other hand, the
differential equation \eqref{rhoeq} implies that the function $\rho$ cannot have a
positive local maximum on the interval $(y_1,y_2)$. So we must have
$\rho(y) \ge \rho(y_1) > 1$ for all $y \in [y_1,y_2)$, and taking the limit $y \to y_2$ we
conclude that $\rho(y_2) = v_2(y_2)/v_1(y_2) > 1$.
To establish the first inequality in \eqref{comp1}, we observe that
$c u_i'(y) = \psi_i(y)\bigl(1 - u_i(y)\bigr)u_i(y)$ for all
$y \in [y_1,y_2]$, where $\psi_i = u_i + dv_i - 1$. We thus have the
integral representation
\begin{equation*}
h(u_i(y)) \,=\, h(u_i(y_1)) \,\exp\left(\frac{1}{c}\int_{y_1}^y
\psi_i(z)\,{\rm d} z \right)\,, \qquad y \in [y_1,y_2]\,,\quad i = 1,2\,,
\end{equation*}
where $h(u) = u/(1-u)$.
In particular,
\begin{equation*}
\frac{h(u_2(y_2))}{h(u_1(y_2))} \,=\, \frac{h(u_2(y_1))}{h(u_1(y_1))}
\,\exp\left(\frac{1}{c}\int_{y_1}^{y_2} \bigl(\psi_2(z)-\psi_1(z)\bigr)
\,{\rm d} z \right) \,>\, \frac{h(u_2(y_1))}{h(u_1(y_1))} \,>\, 1\,,
\end{equation*}
because $\psi_2(y) > \psi_1(y)$ on $(y_1,y_2)$. Thus $u_2(y_2) > u_1(y_2)$,
so that both inequalities in \eqref{comp1} hold at $y = y_2$, which
gives the desired contradiction.
\end{proof}
We recall that the relevant values of the shooting parameter $\alpha > 0$ are those for
which $T(\alpha,c) = +\infty$. Since $T(\alpha,c)$ is a non-decreasing function of $\alpha$
by Lemma~\ref{lem:monotone}, the following definition is natural\thinspace :
\begin{equation}\label{alpha0def}
\alpha_0(c) \,=\, \inf\bigl\{\alpha > 0 \,|\, T(\alpha,c) = +\infty
\bigr\} \,\in\, [0,+\infty]\,.
\end{equation}
Two situations can occur, depending on the value of the speed
parameter $c > 0$\thinspace :
\begin{lem}\label{lem:alpha0}
If $c \ge 2\sqrt{r}$, then $\alpha_0(c) = 0$. If $0 < c < 2\sqrt{r}$,
then $0 < \alpha_0(c) < +\infty$.
\end{lem}
\begin{proof}
If $c \ge 2\sqrt{r}$ ({\em strongly damped case}), we claim that $T(\alpha,c) = +\infty$
for all $\alpha > 0$, so that $\alpha_0(c) = 0$. Indeed, using the continuity properties
mentioned in Remark~\ref{rem:allsol}, it is easy to verify that, in the limit where
$\alpha \to 0$, the solution $(u_{\alpha,c},v_{\alpha,c})$ of \eqref{Ode2} given by
Lemma~\ref{lem:unstab} converges uniformly on compact intervals to $(0,v)$, where
$v : \mathbb{R} \to \mathbb{R}$ is the unique solution of the Fisher--KPP equation
\begin{equation}\label{FKPP}
v'' + c v' + rv(1-v) \,=\, 0\,,
\end{equation}
normalized so that $e^{-\lambda y}(1 - v(y)) \to 1$ as $y \to -\infty$. As is well known,
the Fisher--KPP front $v$ is positive when $c \ge 2\sqrt{r}$. Since $v_{\alpha,c}$ is an
increasing function of $\alpha$ by Lemma~\ref{lem:monotone}, we deduce that
$v_{\alpha,c}(y) > 0$ for all $y \in \mathbb{R}$ and all $\alpha > 0$, which means that
$T(\alpha,c) = +\infty$ for all $\alpha > 0$.
We next consider the opposite situation where $0 < c < 2\sqrt{r}$ ({\em weakly damped
case}). In that case, the solution $v$ of the Fisher--KPP equation is no longer positive,
hence there exists $\bar y \in \mathbb{R}$ so that $v(\bar y) < 0$. By continuity, we have
$v_{\alpha,c}(\bar y) < 0$ when $\alpha > 0$ is sufficiently small, so that
$T(\alpha,c) < +\infty$ for all sufficiently small $\alpha > 0$. To conclude the proof, it
remains to show that $T(\alpha,c) = +\infty$ when $\alpha > 0$ is sufficiently large. It
is convenient here to define $y_0 = (\ln \alpha)/\mu \gg 1$ and to consider the shifted
quantities
\[
\begin{aligned}
\hat u(y) \,&:=\, u_{\alpha,c}(y-y_0) \,=\, e^{\mu y} +
\mathcal{O}\Bigl(e^{(\mu + \eta)y}\Bigr)\,, \\
\hat v(y) \,&:=\, v_{\alpha,c}(y-y_0) \,=\, 1 - \beta\,e^{\lambda y} +
\mathcal{O}\Bigl(e^{(\lambda + \eta)y}\Bigr)\,, \\
\hat w(y) \,&:=\, w_{\alpha,c}(y-y_0) \,=\, - \beta\lambda\,e^{\lambda y} +
\mathcal{O}\Bigl(e^{(\lambda + \eta)y}\Bigr)\,,
\end{aligned}
\qquad \hbox{as}\quad y \to -\infty\,,
\]
where $\beta = \alpha^{-\lambda/\mu} \to 0$ as $\alpha \to +\infty$. On any interval of
the form $(-\infty,y_0]$, these functions converge uniformly to $(\chi,1,0)$ as
$\beta \to 0$, where $\chi$ is the unique solution of the differential equation
\begin{equation*}
c\chi' \,=\, u(1-u)\bigl(d-1 + u\bigr)\,,
\end{equation*}
normalized so that $\chi(y) = e^{\mu y} + \mathcal{O}(e^{2\mu y})$ as $y \to -\infty$. It is
clear that $\chi$ is increasing and converges to $1$ as $y \to +\infty$. Given any small
$\epsilon > 0$, we can therefore choose $y_1 > 0$ large enough and $\beta > 0$ small
enough so that $\hat u(y_1) \ge 1-\epsilon$, as well as $\hat v(y) \ge 1-\epsilon$ and
$\hat v'(y) \ge -\epsilon$ for all $y \le y_1$. In the rest of the proof, we choose
$\epsilon = \epsilon_0/K$ where
\begin{equation}\label{Kdef}
\epsilon_0 \,=\, \frac{d-1}{2d} \,\in\, \Bigl(0\,,\frac12\Bigr)\,,
\qquad \hbox{and}\qquad K \,=\, 1 + \frac{1}{c} + \frac{2r}{d}\,>\, 1\,.
\end{equation}
Under these assumptions, we claim that $\hat v(y) \ge 1 - \epsilon_0$ for all $y \ge y_1$,
which implies that $T(\alpha,c) = +\infty$. Indeed, as long as
$\hat v(y) \ge 1 - \epsilon_0$, the function $\hat u$ satisfies
\[
\hat u'(y) \,=\, \frac{1}{c}\,\hat u(y)\bigl(1-\hat u(y)\bigr)
\bigl(d\hat v(y) - 1 + \hat u(y)\bigr) \,\ge\,
\frac{\mu}{2}\,\hat u(y)\bigl(1-\hat u(y)\bigr)\,,
\]
because $d\hat v - 1 \ge d-1-d\epsilon_0 = d\epsilon_0 = c\mu/2$. Integrating that
inequality for $y \ge y_1$ and recalling that $\hat u(y_1) \ge 1-\epsilon$, we obtain
\begin{equation}\label{hatubd}
\frac{\hat u(y)}{1-\hat u(y)} \,\ge\, \frac{\hat u(y_1)}{1-\hat u(y_1)}
\,e^{\mu(y-y_1)/2} \,\ge\, \frac{1-\epsilon}{\epsilon}\,e^{\mu(y-y_1)/2}\,,
\end{equation}
which shows that $1 - \hat u(y) \le 2\epsilon \,e^{-\mu(y-y_1)/2}$ as long as
$\hat v(y) \ge 1 - \epsilon_0$. Under that hypothesis, the
function $\hat v$ satisfies a differential inequality of the form
$\hat v''(y) + c\hat v'(y) + \delta\,e^{-\gamma (y-y_1)} \ge 0$, where
$\delta = 2r\epsilon \epsilon_0$ and $\gamma = \mu/2$. Integrating
that inequality for $y \ge y_1$ and assuming for simplicity that
$\gamma \neq c$, we obtain
\[
\hat v'(y) \,\ge\, \hat v'(y_1)\,e^{-c(y-y_1)} - \frac{\delta}{c-\gamma}
\,\Bigl(e^{-\gamma (y-y_1)} - e^{-c(y-y_1)}\Bigr)\,,
\]
hence, recalling that $\hat v(y_1) \ge 1-\epsilon$ and $\hat v'(y_1) \ge
-\epsilon$\thinspace :
\begin{align}\nonumber
\hat v(y) \,&\ge\, \hat v(y_1) + \frac{1 - e^{-c(y-y_1)}}{c}\,\hat v'(y_1)
-\frac{\delta}{c-\gamma}\int_{y_1}^y \Bigl(e^{-\gamma (z-y_1)} - e^{-c(z-y_1)}
\Bigr)\,{\rm d} z \\ \label{hatvbd}
\,&>\, \hat v(y_1) + \frac{1}{c}\,\hat v'(y_1) - \frac{\delta}{c\gamma}
\,\ge\, 1 - \epsilon - \frac{\epsilon}{c} - \frac{4r\epsilon\epsilon_0}{
c\mu} \,=\, 1 - K\epsilon\,,
\end{align}
where $K$ is defined in \eqref{Kdef}. Summarizing, inequalities
\eqref{hatubd} and \eqref{hatvbd} together imply that the lower bound
$\hat v(y) \ge 1-\epsilon_0$ holds in fact for all $y \ge y_1$,
so that $T(\alpha,c) = + \infty$ if $\alpha > 0$ is large enough.
\end{proof}
\begin{rem}\label{rem:alpha0}
If $0 < c < 2\sqrt{r}$, then $T(\alpha_0(c),c) = +\infty$. Indeed, if this was not the
case, the solution $v_{\alpha_0(c),c}$ of \eqref{Ode2} defined in Lemma~\ref{lem:unstab}
would cross the origin (with a negative slope) at point
$\bar y = T(\alpha_0(c),c) < +\infty$. By continuity, $v_{\alpha,c}$ would also change
sign near $\bar y$ if $\alpha > \alpha_0(c)$ and $\alpha$ is sufficiently close to
$\alpha_0(c)$. Thus $T(\alpha,c) < +\infty$ for some $\alpha > \alpha_0(c)$, which
contradicts the definition of $\alpha_0(c)$. Summarizing, it follows from
Lemma~\ref{lem:alpha0} that $T(\alpha,c) = +\infty$ for all $\alpha > 0$ when
$c \ge 2\sqrt{r}$, and $T(\alpha,c) = +\infty$ if and only if $\alpha \ge \alpha_0(c)$
when $0 < c < 2\sqrt{r}$.
\end{rem}
\subsection{Asymptotic behavior as $y \to +\infty$}
\label{subsec24}
Using the results obtained so far, we now show that the solutions of \eqref{Ode2} on the
unstable manifold of $S_-$, when they stay in the region defined by \eqref{Ddef}, are
eventually monotone and converge therefore to finite limits as $y \to +\infty$.
\begin{lem}\label{lem:limits}
If $T(\alpha,c) = +\infty$, the following limits exist\thinspace :
\begin{equation}\label{uvlimits}
u_\infty(\alpha,c) \,=\, \lim_{y \to +\infty} u_{\alpha,c}(y)
\in \{0,1\}\,, \qquad
v_\infty(\alpha,c) \,=\, \lim_{y \to +\infty} v_{\alpha,c}(y)
\in [0,1)\,.
\end{equation}
Moreover, if $u_\infty(\alpha,c) = 0$, then $v_\infty(\alpha,c) = 0$.
\end{lem}
\begin{proof}
Assume that $\alpha > 0$ and $c > 0$ are such that $T(\alpha,c) =
+\infty$, which means that the solution $(u,v,w) = (u_{\alpha,c},
v_{\alpha,c},w_{\alpha,c})$ of \eqref{Ode3} is global and stays in the
region $\mathcal{D}$ for all $y \in \mathbb{R}$. In particular, we have $0 < v(y) < 1$ and
$v'(y) = w(y) < 0$ for all $y \in \mathbb{R}$, which proves the existence
of the second limit in \eqref{uvlimits}. As for the function
$u$, there are two possibilities\thinspace :
\begin{itemize}
\item Either $u(y) + dv(y) > 1$ for all $y \in \mathbb{R}$, in which case the first equation in
\eqref{Ode3} shows that $u'(y) > 0$ for all $y \in \mathbb{R}$. As $0 < u(y) < 1$, we deduce
that $u(y)$ converges to some limit $u_\infty \in (0,1]$. Actually, since
$(u_\infty,v_\infty)$ must be an equilibrium of \eqref{Ode3}, we necessarily have
$u_\infty = 1$.
\item Or there exists $\bar y \in \mathbb{R}$ such that $u(\bar y) + dv(\bar y) = 1$. In that
case, by the first equation in \eqref{Ode3}, we have $u'(\bar y) = 0 < - dv'(\bar y)$,
and this implies that $u(y) + dv(y) < 1$ for all $y > \bar y$. The same argument also
shows that $u(y) + dv(y) > 1$ for all $y < \bar y$, in agreement with
\eqref{asym1}. Thus we conclude that $u'(y) > 0$ for all $y < \bar y$, and $u'(y) < 0$
for all $y > \bar y$. In particular $u(y)$ converges to some limit $u_\infty \in [0,1)$
as $y \to +\infty$, and we must have $u_\infty = v_\infty = 0$ since
$(u_\infty,v_\infty)$ is an equilibrium of \eqref{Ode3}.
\end{itemize}
The proof of \eqref{uvlimits} is thus complete.
\end{proof}
It is clear from Lemma~\ref{lem:monotone} that both limits $u_\infty$, $v_\infty$ in
\eqref{uvlimits} are non-decreasing functions of the shooting parameter $\alpha > 0$. Also,
the proof of Lemma~\ref{lem:alpha0} shows that, if $\alpha > 0$ is sufficiently large
(depending on $c$), we necessarily have $u_\infty = 1$ and $v_\infty > 0$. This leads to
the following definition\thinspace :
\begin{equation}\label{alpha1def}
\alpha_1(c) \,=\, \inf\bigl\{\alpha > \alpha_0(c) \,|\,
u_\infty(\alpha,c) = 1\bigr\}\,.
\end{equation}
\begin{lem}\label{lem:alpha1}
For any $c > 0$ we have $0 < \alpha_1(c) < \infty$. Moreover
$\alpha_1(c) = \alpha_0(c)$ if $0 < c < 2\sqrt{r}$.
\end{lem}
\begin{proof}
Fix $c > 0$. We already observed that $u_\infty(\alpha,c) = 1$ when
$\alpha > 0$ is sufficiently large, so that $\alpha_1(c) < +\infty$.
If $c \ge 2\sqrt{r}$, so that $\alpha_0(c) = 0$ by Lemma~\ref{lem:alpha0},
we recall that the solution $(u_{\alpha,c},v_{\alpha,c})$ of \eqref{Ode2}
converges uniformly on compact sets to $(0,v)$ as $\alpha \to 0$,
where $v$ is the Fisher--KPP front. Since $v(y) \to 0$ as $y \to
+\infty$, we can choose $y \in \mathbb{R}$ so that $v(y) < 1/d$. If
$\alpha > 0$ is sufficiently small, we thus have $u_{\alpha,c}(y)
+ dv_{\alpha,c}(y) < 1$, and the proof of Lemma~\ref{lem:limits}
then shows that $u_\infty(\alpha,c) = 0$. Thus $\alpha_1(c) > 0$.
It remains to show that $\alpha_1(c) = \alpha_0(c)$ when $0 < c < 2\sqrt{r}$. Indeed, if
$\alpha_1(c) > \alpha_0(c)$, we can take $\alpha \in (\alpha_0(c),\alpha_1(c))$ so that
the corresponding solution $(u,v,w) = (u_{\alpha,c},v_{\alpha,c},w_{\alpha,c})$ of
\eqref{Ode3} stays in $\mathcal{D}$ for all $y \in \mathbb{R}$. Moreover $u_\infty = v_\infty = 0$ since
$\alpha < \alpha_1(c)$. We choose $\epsilon > 0$ small enough so that
$c < 2\sqrt{r}(1-\epsilon)$, and $\bar y > 0$ large enough so that $u(y) < \epsilon$ and
$v(y) < \epsilon$ for all $y \ge \bar y$. All solutions of the constant coefficient ODE
\[
v''(y) + cv'(y) + r(1-\epsilon)^2 v(y) \,=\, 0\,, \qquad
y \in \mathbb{R}\,,
\]
have infinitely many zeros in the interval $(\bar y,+\infty)$, and Sturm's comparison
theorem asserts that the function $v_{\alpha,c}$, which satisfies the second equation in
\eqref{Ode2} where $(1-u)(1-v) > (1-\epsilon)^2$, has a fortiori infinitely many zeros in
that interval, see e.g. \cite[Chapter~8]{CL}. This of course contradicts the assumption
that $\alpha > \alpha_0(c)$.
\end{proof}
\begin{rem}\label{rem:alpha1}
It follows from Remark~\ref{rem:alpha0} that $T(\alpha_1(c),c) = +\infty$
for any $c > 0$. It is also easy to verify that $u_\infty(\alpha_1(c),c) = 1$.
Indeed, if this is not the case, we have $u_\infty(\alpha,c) = v_\infty(\alpha,c)
= 0$ by Lemma~\ref{lem:limits}, where $\alpha = \alpha_1(c)$, hence we
can take $\bar y \in \mathbb{R}$ large enough so that $u_{\alpha,c}(\bar y) +
d v_{\alpha,c}(\bar y) < 1$. By continuity, we then have $u_{\alpha',c}(\bar y) +
d v_{\alpha',c}(\bar y) < 1$ for any $\alpha'$ sufficiently close to $\alpha$, so
that $u_\infty(\alpha',c) = 0$ for some $\alpha' > \alpha_1(c)$, in contradiction
with the definition of $\alpha_1(c)$. It is more difficult to prove
that $v_\infty(\alpha_1(c),c) = 0$; this is precisely the purpose
of the next section.
\end{rem}
\subsection{The center manifold of the healthy state}
\label{subsec25}
Given any $c > 0$, we assume from now on that $\alpha \ge \alpha_1(c)$.
In that case, we know from Remark~\ref{rem:alpha1} that $T(\alpha,c) =
+\infty$ and that the solution $(u_{\alpha,c},v_{\alpha,c}, w_{\alpha,c})$
of \eqref{Ode3} given by Lemma~\ref{lem:unstab} converges to
$\bigl(1,v_\infty(\alpha,c),0\bigr)$ as $y \to + \infty$,
where $0 \le v_\infty(\alpha,c) < 1$. Our goal is to determine
for which value(s) of $\alpha$ we have $v_\infty(\alpha,c) = 0$,
so that the boundary conditions \eqref{BC3} are satisfied.
To study the dynamics of the ODE system \eqref{Ode3} in a
neighborhood of the healthy equilibrium $S_+ = (1,0,0)$,
we introduce the new dependent variables
\begin{equation}\label{tildeuvw}
\tilde u(y) \,=\, 1 - u(y)\,, \qquad \tilde v(y)
\,=\, v(y) + w(y)/c\,, \qquad \tilde w(y) = w(y)/c\,,
\end{equation}
which satisfy the modified system
\begin{align}\nonumber
\tilde u' \,&=\, \frac{1}{c}\,\tilde u(1-\tilde u)(\tilde u - d\tilde v
+ d\tilde w)\,, \\ \label{Ode4}
\tilde v' \,&=\, -\frac{r}{c}\,\tilde u(\tilde v -\tilde w)(1-
\tilde v + \tilde w)\,, \\ \nonumber
\tilde w' \,&=\, -c \tilde w - \frac{r}{c}\,\tilde u(\tilde v -\tilde w)
(1-\tilde v + \tilde w)\,.
\end{align}
It is clear that $(\tilde u,\tilde v,\tilde w) = (0,v_\infty,0)$ is an equilibrium of
\eqref{Ode4} for any $v_\infty \in \mathbb{R}$, and that the healthy state $S_+$ corresponds to
$v_\infty = 0$. The linearization of \eqref{Ode4} at the origin is easily found to be
$\tilde u' = 0$, $\tilde v' = 0$, $\tilde w' = -c\tilde w$. It follows that all solutions
of \eqref{Ode4} that stay in a small neighborhood of the origin for all sufficiently large
$y > 0$ converge as $y \to +\infty$ to a two-dimensional center manifold
$\mathcal{W} \subset \mathbb{R}^3$, which is tangent at the origin to the subspace spanned by the vectors
$(1,0,0)$ and $(0,1,0)$. For any $k \in \mathbb{N}$, the center manifold is locally the graph of a
$C^k$ function $\mathcal{F}$, so that $(\tilde u,\tilde v,\tilde w) \in \mathcal{W}$ if and only if
$\tilde w = \mathcal{F}(\tilde u,\tilde v)$ where
\begin{equation}\label{cFdef}
\mathcal{F}(\tilde u,\tilde v) \,=\,
-\frac{r}{c^2}\,\tilde u\tilde v \Bigl(1 +
\mathcal{O}(|\tilde u| + |\tilde v|)\Bigr)\,,
\qquad \hbox{as} \quad (\tilde u,\tilde v) \to
(0,0)\,.
\end{equation}
We recall that the center manifold $\mathcal{W}$ and the associated function $\mathcal{F}$ are not
necessarily unique, but the asymptotic expansion in \eqref{cFdef} is free of ambiguity,
see e.g. \cite[Chapter~3]{GH}. Moreover, any center manifold $\mathcal{W}$ necessarily contains
the equilibria $(0,v_\infty,0)$ for sufficiently small values of $v_\infty$. The
derivation of \eqref{cFdef} is standard, see \cite{CLW,GH,HI} for the methodology and
several examples. We just observe here that $\mathcal{F}(0,\tilde v) = 0$ because the dynamics of
\eqref{Ode4} is trivial when $\tilde u = 0$, and that $\mathcal{F}(\tilde u,0) = 0$ because the
subspace defined by $\tilde v = \tilde w = 0$ is invariant under the evolution defined by
\eqref{Ode4}.
Since we are interested in solutions of \eqref{Ode3} that stay in the region $\mathcal{D}$ defined
by \eqref{Ddef}, it is natural to consider solutions of \eqref{Ode4} on the smaller
manifold
\[
\mathcal{W}_+ \,=\, \bigl\{(\tilde u,\tilde v,\tilde w) \in
\mathcal{W} \,\big|\, \tilde u > 0\,,~\tilde v > 0\bigr\}\,.
\]
We first study the solutions of \eqref{Ode4} which
converge to zero as $y \to +\infty$.
\begin{lem}\label{lem:Wzero}
Up to translations in the variable $y$, there exists a unique
solution of \eqref{Ode4} on the center manifold $\mathcal{W}_+$ which
converges to zero as $y \to +\infty$. This solution
satisfies
\begin{equation}\label{asym2}
\tilde u(y) \,=\, \frac{c}{ry} + \mathcal{O}\Bigl(\frac{1}{y^2}
\Bigr)\,, \qquad
\tilde v(y) \,=\, \frac{c(1+r)}{dry} + \mathcal{O}\Bigl(\frac{1}{y^2}
\Bigr)\,, \qquad \hbox{as } y \to +\infty\,.
\end{equation}
\end{lem}
\begin{proof}
We first prove the existence of a solution of \eqref{Ode4} on $\mathcal{W}_+$
which converges to zero as $y \to +\infty$. We perform the
change of variables
\begin{equation}\label{fgdef}
\tilde u(y) \,=\, \frac{a}{y}\,f\bigl(\ln y\bigr)\,, \qquad
\tilde v(y) \,=\, \frac{b}{y}\,g\bigl(\ln y\bigr)\,, \qquad
z \,=\, \ln y\,,
\end{equation}
where $a = c/r$ and $b = c(1+r)/(dr)$. If $\tilde u,\tilde v$
evolve according to \eqref{Ode4} with $\tilde w = \mathcal{F}(\tilde u,\tilde v)$,
the new functions $f(z),g(z)$ satisfy the system
\begin{equation}\label{fgsys}
\begin{aligned}
f' \,&=\, f + \frac{1}{c}f\Bigl(1 - a e^{-z}f\Bigr)
\Bigl(af -db g + d e^{-z} \mathcal{R}(f,g,z)\Bigr)\,, \\
g' \,&=\, g - \frac{1}{b}f\Bigl(bg - e^{-z}\mathcal{R}(f,g,z)\Bigr)
\Bigl(1 - b e^{-z}g + e^{-2z}\mathcal{R}(f,g,z)\Bigr)\,,
\end{aligned}
\end{equation}
where $\mathcal{R}(f,g,z) = e^{2z}\mathcal{F}(a e^{-z}f,be^{-z}g)$ and ${}'$ now
denotes differentiation with respect to the new variable
$z = \ln y$. As $|\mathcal{R}(f,g,z)| \le C |f| |g|$ by \eqref{cFdef},
we see that the non-autonomous system \eqref{fgsys} converges
as $z \to +\infty$ to
\begin{equation}\label{fglimit}
f' \,=\, f \left\{1 + \frac{1}{r}f - \left(1 + \frac{1}{r}\right) g\right\}\,,
\qquad g' \,=\, g\bigl(1 - f\bigr)\,.
\end{equation}
This limiting system has a unique positive equilibrium $(\bar f,\bar g) = (1,1)$, which is
hyperbolic, and the eigenvalues of the linearized operator are easily found to be
$1 + 1/r$ and $-1$. Applying the stable manifold theorem, we deduce that there exists a
solution $(f,g)$ of \eqref{fgsys} which converges to $(1,1)$ as $z \to +\infty$ and
satisfies $|f(z) - 1| + |g(z)-1| = \mathcal{O}(e^{-z})$ in this limit. Returning to the original
variables, we conclude that the solution of \eqref{Ode4} on $\mathcal{W}_+$ given by \eqref{fgdef}
converges to $(0,0)$ as $y \to +\infty$ and satisfies \eqref{asym2}.
To prove uniqueness, it is convenient to write the evolution
equations on the center manifold $\mathcal{W}_+$ in the condensed form
\begin{equation}\label{uvreduc}
\tilde u' \,=\, \mathcal{G}(\tilde u,\tilde v)\,, \qquad
\tilde v' \,=\, \mathcal{H}(\tilde u,\tilde v)\,,
\end{equation}
where
\begin{equation}\label{GHdef}
\begin{aligned}
\mathcal{G}(\tilde u,\tilde v) \,&=\, \frac{1}{c}\,\tilde u(1-\tilde u)
\bigl(\tilde u - d\tilde v + d\mathcal{F}(\tilde u,\tilde v)\bigr)\,, \\
\mathcal{H}(\tilde u,\tilde v) \,&=\, -\frac{r}{c}\,\tilde u\bigl(\tilde v -
\mathcal{F}(\tilde u,\tilde v)\bigr)\bigr(1- \tilde v + \mathcal{F}(\tilde u,
\tilde v)\bigr)\,.
\end{aligned}
\end{equation}
The solution $(\tilde u,\tilde v)$ of \eqref{uvreduc} constructed in
the previous step satisfies $\tilde v = \Psi(\tilde u)$ in some
$\epsilon$-neighborhood of the origin, where $\Psi : (0,\epsilon)
\to \mathbb{R}_+$ is a $C^k$ function satisfying the functional relation
\begin{equation}\label{funcrel}
\mathcal{H}\bigl(x,\Psi(x)\bigr) \,=\, \Psi'(x)\,\mathcal{G}\bigl(x,\Psi(x)\bigr)\,,
\qquad x \in (0,\epsilon)\,.
\end{equation}
Moreover, in agreement with \eqref{asym2}, we have $\Psi(x) =
(1+r)x/d + \mathcal{O}(x^2)$ as $x \to 0$.
Now, we consider an {\em arbitrary} positive solution $(\tilde u,\tilde v)$
of \eqref{uvreduc} that converges to the origin as $y \to +\infty$.
Using \eqref{funcrel}, we observe that
\begin{align}\nonumber
\frac{{\rm d}}{{\rm d} y}\bigl(\tilde v - \Psi(\tilde u)\bigr) \,&=\,
\mathcal{H}\bigl(\tilde u,\tilde v\bigr) - \Psi'(\tilde u)\,
\mathcal{G}\bigl(\tilde u,\tilde v\bigr) \\[-1mm] \label{diffeq}
\,&=\, \mathcal{H}\bigl(\tilde u,\tilde v\bigr) - \mathcal{H}\bigl(\tilde u,
\Psi(\tilde u)\bigr) - \Psi'(\tilde u)\Bigl(\mathcal{G}\bigl(\tilde u,
\tilde v\bigr) - \mathcal{G}\bigl(\tilde u,\Psi(\tilde u)\bigr)\Bigr) \\
\nonumber
\,&=\, {\rm d}elta(\tilde u,\tilde v)\bigl(\tilde v - \Psi(\tilde u)\bigr)\,,
\end{align}
where
\[
{\rm d}elta(\tilde u,\tilde v) \,=\, \int_0^1 \Bigl(\partial_2
\mathcal{H}\bigl(\tilde u,(1-t)\Psi(\tilde u)+t \tilde v\bigr) -
\Psi'(\tilde u)\,\partial_2 \mathcal{G}\bigl(\tilde u,(1-t)\Psi(\tilde u)
+t \tilde v\bigr)\Bigr)\,{\rm d} t\,.
\]
Using \eqref{cFdef} and \eqref{GHdef}, it is straightforward to
compute an asymptotic expansion of ${\rm d}elta(\tilde u,\tilde v)$
as $(\tilde u,\tilde v) \to (0,0)$, which is found to be
${\rm d}elta(\tilde u,\tilde v) = c^{-1}\tilde u \bigl(1 + \mathcal{O}(|\tilde u| +
|\tilde v|)\bigr)$. In particular ${\rm d}elta(\tilde u,\tilde v) > 0$ for
small solutions on $\mathcal{W}_+$. Keeping that observation in mind,
we integrate \eqref{diffeq} on the interval $[y_1,y_2]$ for $y_1 > 0$
sufficiently large and obtain the relation
\[
\tilde v(y_2) - \Psi(\tilde u(y_2)) \,=\, \exp\Bigl(
\int_{y_1}^{y_2} {\rm d}elta(\tilde u(y),\tilde v(y))\,{\rm d} y\Bigr)
\Bigl(\tilde v(y_1) - \Psi(\tilde u(y_1))\Bigr)\,,
\]
which implies that $|\tilde v(y_2) - \Psi(\tilde u(y_2))| \ge
|\tilde v(y_1) - \Psi(\tilde u(y_1))|$. By assumption, the
left-hand side converges to zero as $y_2 \to +\infty$,
and we conclude that $\tilde v(y_1) = \Psi(\tilde u(y_1))$ for all
(sufficiently large) $y_1 > 0$. This precisely means that
$(\tilde u,\tilde v)$ coincides, up to a translation in the
variable $y$, with the solution of \eqref{uvreduc} constructed
in the first step.
\end{proof}
Since a whole neighborhood of the origin in $\mathbb{R}^3$ is foliated by
one-dimensional strong stable leaves over the two-dimensional center
manifold $\mathcal{W}$, see \cite{CLW}, we can extract from Lemma~\ref{lem:Wzero}
useful information on the asymptotic behavior as $y \to +\infty$
of the traveling waves of the original system \eqref{Ode3}.
As a first application, we prove uniqueness of the traveling wave
for each value of the speed parameter.
\begin{lem}\label{lem:unique}
Given any $c > 0$, there exists at most one value $\alpha \ge
\alpha_1(c)$ of the shooting parameter such that the solution
$(u_{\alpha,c}(y),v_{\alpha,c}(y),w_{\alpha,c}(y))$ of \eqref{Ode3} given
by Lemma~\ref{lem:unstab} converges to $S_+ = (1,0,0)$ as $y \to +\infty$.
\end{lem}
\begin{proof}
Assume that, for some $\alpha \ge \alpha_1(c)$, the solution
$(u_{\alpha,c},v_{\alpha,c},w_{\alpha,c})$ of \eqref{Ode3}
converges to $S_+ = (1,0,0)$ as $y \to +\infty$. We denote by
$(\tilde u_{\alpha,c},\tilde v_{\alpha,c},\tilde w_{\alpha,c})$
the corresponding solution of \eqref{Ode4}, given by the
change of variables \eqref{tildeuvw}. We first observe that
$(\tilde u_{\alpha,c},\tilde v_{\alpha,c},\tilde w_{\alpha,c})$
does not lie on the strong stable manifold of the origin
$(0,0,0)$, because that manifold consists of solutions
of \eqref{Ode4} satisfying $\tilde u' = \tilde v' = 0$, $\tilde
w' = -c \tilde w$. Thus $(\tilde u_{\alpha,c},\tilde v_{\alpha,c},
\tilde w_{\alpha,c})$ approaches exponentially fast a nontrivial
solution $(\tilde u,\tilde v)$ on the center manifold $\mathcal{W}_+$,
which converges itself to $(0,0)$ as $y \to +\infty$.
Using Lemma~\ref{lem:Wzero}, we conclude that the pair
$(\tilde u_{\alpha,c},\tilde v_{\alpha,c})$ satisfies the
asymptotic expansion \eqref{asym2}, and that $\tilde
w_{\alpha,c} = \mathcal{F}(\tilde u_{\alpha,c},\tilde v_{\alpha,c})$
up to exponentially small corrections as $y \to +\infty$.
Now suppose that another solution $(u_{\alpha'\!,c},v_{\alpha'\!,c}, w_{\alpha'\!,c})$
also converges to $S_+$. If $\alpha' > \alpha$, the proof of Lemma~\ref{lem:monotone}
shows that there exists $\rho > 1$ such that $v_{\alpha'\!,c}(y)/v_{\alpha,c}(y) \ge \rho$
for all sufficiently large $y > 0$. On the other hand, since the asymptotic behavior of
both solutions is given by \eqref{asym2}, as is explained above, it follows from
\eqref{tildeuvw} and \eqref{cFdef} that
\[
\lim_{y \to +\infty} \frac{v_{\alpha'\!,c}(y)}{v_{\alpha,c}(y)}
\,=\, \lim_{y \to +\infty} \frac{\tilde v_{\alpha'\!,c}(y)}{\tilde
v_{\alpha,c}(y)} \,=\, 1\,,
\]
which gives a contradiction. So we must have $\alpha' = \alpha$
and uniqueness is established.
\end{proof}
We now prove the main result of this section, namely the
existence of a traveling wave connecting the infected
state $S_-$ to the healthy state $S_+$.
\begin{lem}\label{lem:exist}
If $c > 0$ and $\alpha = \alpha_1(c)$, the solution $(u_{\alpha,c},
v_{\alpha,c},w_{\alpha,c})$ of \eqref{Ode3} given by
Lemma~\ref{lem:monotone} converges to $S_+ = (1,0,0)$ as
$y \to +\infty$.
\end{lem}
\begin{proof}
Fix $\alpha = \alpha_1(c)$. We already know that
$(u_{\alpha,c}(y),v_{\alpha,c}(y),w_{\alpha,c}(y))$ converges to
$(1,v_\infty,0)$ as $y \to +\infty$, for some $v_\infty \in [0,1)$. If
$v_\infty > 0$, we obtain a contradiction as follows. We perform
again the change of variables \eqref{tildeuvw} and consider system
\eqref{Ode4} near the equilibrium $(0,v_\infty,0)$. The
linearization at this point is given by
\[
\tilde u' \,=\, -\frac{dv_\infty}{c}\,\tilde u\,, \qquad
\tilde v' \,=\, -\frac{rv_\infty}{c}(1-v_\infty)\,\tilde u\,, \qquad
\tilde w' \,=\, -c \tilde w -\frac{rv_\infty}{c}(1-v_\infty)\,\tilde u
\,.
\]
In contrast to the situation where $v_\infty = 0$, which was studied
previously, the zero eigenvalue is now simple, with eigenvector
$(0,1,0)$, and there are two negative eigenvalues $-dv_\infty/c$ and
$-c$. Applying the center manifold theorem again, we deduce that there
exists a small open neighborhood $\Omega$ of $(0,v_\infty,0)$ in
$\mathbb{R}^3$ that is foliated by two-dimensional stable leaves over a
one-dimensional center manifold, which itself consists of the family
of equilibria $(0,v,0)$ with $v$ close enough to $v_\infty$. Taking a
smaller neighborhood if needed, we can make sure that, for all initial
data in $\Omega$, the solution of \eqref{Ode4} converges to $(0,\bar
v,0)$ as $y \to +\infty$, for some $\bar v > 0$.
Now let $(\tilde u_{\alpha,c},\tilde v_{\alpha,c},\tilde w_{\alpha,c})$
denote the solution of \eqref{Ode4} obtained from $(u_{\alpha,c},
v_{\alpha,c},w_{\alpha,c})$ by the change of variables \eqref{tildeuvw}.
By assumption $(\tilde u_{\alpha,c}(y),\tilde v_{\alpha,c}(y),\tilde
w_{\alpha,c}(y))$ converges to $(0,v_\infty,0)$ as $y \to +\infty$, hence
there exists $\bar y \in \mathbb{R}$ such that $(\tilde u_{\alpha,c}(y),\tilde
v_{\alpha,c}(y), \tilde w_{\alpha,c}(y)) \in \Omega$ for all $y \ge \bar y$.
By continuity, we infer that $(\tilde u_{\alpha'\!,c}(\bar y),\tilde
v_{\alpha'\!,c}(\bar y), \tilde w_{\alpha'\!,c}(\bar y)) \in \Omega$ if
$\alpha' < \alpha$ is sufficiently close to $\alpha$, which means
that $(u_{\alpha'\!,c}(y),v_{\alpha'\!,c}(y),w_{\alpha'\!,c}(y))$ converges
to $(1,\bar v,0)$ as $y \to +\infty$ for some $\bar v > 0$. As $\alpha' <
\alpha = \alpha_1(c)$, this clearly contradicts definition \eqref{alpha1def}.
So we must have $v_\infty(\alpha,c) = 0$.
\end{proof}
\begin{rem}\label{rem:monotone}
Using similar arguments, one can also show that the map
$\alpha \mapsto v_\infty(\alpha,c)$ is continuous and strictly
increasing for $\alpha \ge \alpha_1(c)$.
\end{rem}
\subsection{Asymptotic behavior in the original variables}
\label{subsec26}
It is now an easy task to complete to proof of Theorem~\ref{main1}. Given any
$c > 0$, we denote $\alpha = \alpha_1(c) > 0$, where $\alpha_1(c)$ is defined
in \eqref{alpha1def}. We know from Lemma~\ref{lem:exist} that the solution $(u,v,w) =
(u_{\alpha,c},v_{\alpha,c}, w_{\alpha,c})$ of \eqref{Ode3} given by Lemma~\ref{lem:unstab}
converges to $S_+ = (1,0,0)$ as $y \to +\infty$, so that the boundary conditions
\eqref{BC3} are satisfied. We now undo the change of variables \eqref{ydef}, which in
view of \eqref{uvdef} can be written in the equivalent form
\begin{equation}\label{xidef}
\frac{{\rm d} \xi}{{\rm d} y} \,\equiv\, \bigl(\Phi^{-1}\bigr)'(y)
\,=\, 1 - u(y)\,, \qquad y \in \mathbb{R}\,.
\end{equation}
Specifically, we define
\begin{equation}\label{xiexp}
\xi(y) \,=\, \Phi^{-1}(y) \,=\, y - \int_{-\infty}^y
u(y')\,{\rm d} y'\,, \qquad y \in \mathbb{R}\,.
\end{equation}
Using the asymptotic expansions \eqref{asym1} as $y \to -\infty$ and \eqref{asym2}
as $y \to +\infty$, it is straightforward to verify that
\begin{equation}\label{Phiminus}
\Phi^{-1}(y) \,=\, \begin{cases}
y - \frac{\alpha}{\mu}\,e^{\mu y} + \mathcal{O}\Bigl(e^{(\mu+\eta)y}\Bigr)
& \hbox{as} \quad y \to -\infty\,, \\
\frac{c}{r}\,\ln(y) + \xi_0 + \mathcal{O}\Bigl(\frac{1}{y}\Bigr)
& \hbox{as} \quad y \to +\infty\,, \\
\end{cases}
\end{equation}
for some $\xi_0 \in \mathbb{R}$. At this point, it is important to note that $\xi(y)
\to +\infty$ as $y \to +\infty$, so that $\bar\xi = +\infty$ in the terminology
of Lemma~\ref{lem:sharp}. Sharp fronts of the original system \eqref{Ode1}
would correspond to solutions of \eqref{Ode3} satisfying $\int_0^{+\infty}
(1{-}u)\,{\rm d} y < \infty$, which are excluded by Lemma~\ref{lem:Wzero}. Inverting
\eqref{Phiminus}, we easily find
\begin{equation}\label{Phiplus}
\Phi(\xi) \,=\, \begin{cases}
\xi + \frac{\alpha}{\mu}\,e^{\mu \xi} + \mathcal{O}\Bigl(e^{(\mu+\eta)\xi}\Bigr)
& \hbox{as} \quad \xi \to -\infty\,, \\
e^{\gamma(\xi-\xi_0)} + \mathcal{O}(1)
& \hbox{as} \quad \xi \to +\infty\,, \\
\end{cases}
\end{equation}
where $\gamma = r/c$. Finally, defining $\mathcal{U}(\xi) = u(\Phi(\xi))$
and $\mathcal{V}(\xi) = v(\Phi(\xi))$ in agreement with \eqref{uvdef},
we obtain by construction a solution of \eqref{Ode1} which
satisfies the boundary conditions \eqref{BC1}. Since $u'(y) < 0$
and $v'(y) > 0$ for all $y \in \mathbb{R}$, it is clear that $\mathcal{U}'(\xi) < 0$
and $\mathcal{V}'(\xi) > 0$ for all $\xi \in \mathbb{R}$, and the asymptotic
expansions \eqref{AsymUV1}, \eqref{AsymUV2} are direct consequences
of \eqref{asym1}, \eqref{asym2}, and \eqref{Phiplus}. For any
$c > 0$, the uniqueness (up to translations) of the solution of
\eqref{Ode1} satisfying \eqref{BC1} is a consequence of
Lemma~\ref{lem:unique}. The proof of Theorem~\ref{main1}
is thus complete. \mathbb{Q}ED
\begin{figure}
\caption{{\small The profile of the same propagation front is represented in
the desingularized variables (left) and in the original variables (right).
The values of the parameters are $d = 2$, $r = 5$, and $c = 0.5$.
Note that $1-u(y)$ and $v(y)$ converge slowly to zero as $y \to +\infty$,
in agreement with \eqref{asym2}
\label{fig3}
\end{figure}
\subsection{Existence of traveling waves when $d < 1$}
\label{subsec27}
Since the beginning of Section~\ref{subsec22}, we assumed that the
parameter $d$ in \eqref{redGGsys} is larger than one, which seems to be
the most relevant situation in cancerology, see \cite{McGiEtAl14}.
For completeness, we now consider the opposite case where $0 < d < 1$.
The analysis being very similar, we just indicate how the proof of
Theorem~\ref{main1} can be modified to obtain the conclusions of
Theorem~\ref{main2}.
Our starting point is again the desingularized system \eqref{Ode3},
which has now the following nontrivial equilibria\thinspace : the infected state
$S_- = (0,1,0)$, the healthy state $S_+ = (1,0,0)$, the coexistence
state $S_d = (1-d,1,0)$, and the artificial equilibria
$(1,v_\infty,0)$ where $v_\infty \neq 0$. The first important
observation is that there exists no traveling wave connecting $S_-$ to
$S_+$ in that case. Indeed, it is clear from the linearization
\eqref{linS-} that the unstable manifold of the infected state $S_-$
is one-dimensional when $d < 1$. Solutions on that manifold are of
the form $(0,v,v')$, where $v$ solves the Fisher--KPP equation
\eqref{FKPP} and $v(y) \to 1$ as $y \to -\infty$.
Since $u$ is equal to $0$ on the unstable manifold, we never obtain a
heteroclinic connection between $S_-$ and $S_+$.
We now consider solutions on the unstable manifold of the
coexistence state $S_d = (1-d,1,0)$. Linearizing \eqref{Ode3}
at $S_d$, we obtain
\begin{equation}\label{linSd}
\tilde u' \,=\, \frac{d(1-d)}{c}\,\bigl(\tilde u - d\tilde v\bigr)\,,
\qquad \tilde v ' \,=\, - w\,, \qquad w' \,=\, -cw -dr\tilde v\,,
\end{equation}
where $\tilde u = u - 1 + d$ and $\tilde v = 1 - v$. We thus find
two positive eigenvalues
\begin{equation}\label{lamudef2}
\lambda \,=\, \frac12\bigl(-c + \sqrt{c^2 + 4dr}\bigr) \,>\, 0\,,
\qquad \mu \,=\, \frac{d(1-d)}{c} \,>\, 0\,,
\end{equation}
as well as one negative eigenvalue $-\frac12\bigl(c + \sqrt{c^2 + 4dr}
\bigr) < 0$. So we again have a two-dimensional unstable manifold,
and the analogue of Lemma~\ref{lem:unstab} is\thinspace :
\begin{lem}\label{lem:unstab2} For any $\alpha \in \mathbb{R}$,
the ODE system \eqref{Ode3} has a unique solution such that
\begin{equation}\label{asym3}
\begin{aligned}
u(y) \,&=\, 1 - d + \alpha\,e^{\mu y} + \frac{d\mu}{\mu-\lambda}
\Bigl(e^{\lambda y} - e^{\mu y}\Bigr) + \mathcal{O}\Bigl(e^{(\mu + \eta)y}
\Bigr)\,, \\
v(y) \,&=\, 1 - e^{\lambda y} + \mathcal{O}\Bigl(e^{(\lambda + \eta)y}\Bigr)\,,
\quad
w(y) \,=\, - \lambda\,e^{\lambda y} + \mathcal{O}\Bigl(e^{(\lambda + \eta)y}\Bigr)\,,
\end{aligned}
\end{equation}
as $y \to -\infty$, where $\lambda,\mu$ are given by \eqref{lamudef2}
and $\eta = \min(\lambda,\mu) > 0$.
\end{lem}
Of course, in the particular case where $\lambda = \mu$, the first
equation in \eqref{asym3} should read
\[
u(y) \,=\, 1 - d + \bigl(\alpha - d\mu y\bigr)\,e^{\mu y}
+ \mathcal{O}\Bigl(e^{2\mu y}\Bigr)\,, \qquad \hbox{as }y \to -\infty\,.
\]
The main difference with Lemma~\ref{lem:unstab} is that the shooting parameter $\alpha$
can take arbitrary values in $\mathbb{R}$, and is not requested to be positive. The reason is that
we look for solutions of \eqref{Ode3} that lie in the region $\mathcal{D}$ defined by
\eqref{Ddef}, which is the case of all solutions \eqref{asym3} in the asymptotic regime
$y \to -\infty$, even if $\alpha < 0$.
As in the proof of Theorem~\ref{main1}, the strategy is to find an appropriate value of
the shooting parameter $\alpha \in \mathbb{R}$ so that the solution of \eqref{Ode3} defined by
\eqref{asym3} converges to $S_+$ as $y \to +\infty$. We first observe that
Lemma~\ref{lem:invariance} still holds, so that we can define $T(\alpha,c)$ by
\eqref{Tdef} for all $\alpha \in \mathbb{R}$. Next, as in Lemma~\ref{lem:monotone}, we claim that
$T(\alpha,c)$ is an increasing function of $\alpha$ and that inequalities \eqref{comp1}
hold when $\alpha_2 > \alpha_1$ and $y \in (-\infty,T(\alpha_1,c))$. The first part of the
proof of Lemma~\ref{lem:monotone} uses a Taylor approximation of system \eqref{Ode3} near
$S_-$ and must therefore be modified since the starting point is now the coexistence state
$S_d \neq S_-$. It is clear from \eqref{asym3} that $u_{\alpha_2,c}(y) > u_{\alpha_1,c}(y)$
when $y < 0$ is sufficiently large, and straightforward calculations show that the
expression \eqref{omexp} of $\omega(y) = e^{-\lambda y}\bigl( v_{\alpha_2,c}(y) -
v_{\alpha_1,c}(y)\bigr)$ has to be replaced by
\begin{equation}\label{omexp2}
\omega(y) \,=\, \frac{r(\alpha_2 - \alpha_1)}{\mu(\mu+
\sqrt{\mu^2 + 4rd})}\,e^{\mu y} + \mathcal{O}\Bigl(e^{(\mu + \eta)y}\Bigr)\,,
\qquad \hbox{as }y \to -\infty\,.
\end{equation}
We deduce as before that inequalities \eqref{comp1} holds when $y < 0$ is large
enough, and the second part of the proof is unchanged.
As in \eqref{alpha0def}, we define
\begin{equation}\label{alpha0def2}
\alpha_0(c) \,=\, \inf\bigl\{\alpha \in \mathbb{R} \,|\, T(\alpha,c) = +\infty
\bigr\} \,\in\, [-\infty,+\infty]\,,
\end{equation}
and we have the following analogue of Lemma~\ref{lem:alpha0}\thinspace :
\begin{lem}\label{lem:alpha02}
If $c \ge 2\sqrt{r}$, then $\alpha_0(c) = -\infty$. If $0 < c < 2\sqrt{r}$,
then $-\infty < \alpha_0(c) < +\infty$.
\end{lem}
\begin{proof}
If $(u_{\alpha,c},v_{\alpha,c},w_{\alpha,c})$ denotes the solution of \eqref{Ode3}
satisfying \eqref{asym3}, and $v$ is the solution of the Fisher--KPP equation
\eqref{FKPP} normalized so that $e^{-\lambda y}(1-v(y)) \to 1$ as $y \to -\infty$,
we first observe that $v_{\alpha,c}(y) > v(y)$ as long as $v(y) > 0$, because
\[
v_{\alpha,c}'' + cv_{\alpha,c}' + rv_{\alpha,c}(1-v_{\alpha,c})
\,>\, v_{\alpha,c}'' + cv_{\alpha,c}' + rv_{\alpha,c}(1-u_{\alpha,c})
(1-v_{\alpha,c}) \,=\, 0\,.
\]
If $c \ge 2\sqrt{r}$, we know that the Fisher--KPP front $v$ remains positive, and this
implies that $T(\alpha,c) = + \infty$ for all $\alpha \in \mathbb{R}$.
In the weakly damped case where $0 < c < 2\sqrt{r}$, we use the same arguments as in the
proof of Lemma~\ref{lem:alpha0}, with suitable modifications. First, if $\alpha < 0$ is
large enough, one can prove verify \eqref{asym3} that the quantity $u(y) + d v(y) - 1$
takes negative values for some (large) $y < 0$. This is obvious when $\mu < \lambda$,
because any sufficiently large $y < 0$ has the desired property, but if $\mu > \lambda$
one has to choose $y$ such that $-(\log|\alpha|)/(\mu{-}\lambda) \ll y \ll
-(\log|\alpha|)/\mu$ (the details being left to the reader). Therefore, assuming that
$T(\alpha,c) = +\infty$, we deduce as in the proof of Lemma~\ref{lem:limits} that
$u_{\alpha,c}(y) \to 0$ as $y \to +\infty$. This in turn implies, as in the proof of
Lemma~\ref{lem:alpha1}, that $v_{\alpha,c}(y)$ satisfies a weakly damped Fisher--KPP
equation for large $y$, and must therefore change sign, which gives a contradiction. So
$T(\alpha,c) < \infty$ if $\alpha < 0$ is sufficiently large.
Finally, if $\alpha > 0$ is large enough, we prove as in Lemma~\ref{lem:alpha0} that the
function $u_{\alpha,c}$ converges to $1$ so rapidly that the non-linearity in the equation
for $v_{\alpha,c}$ becomes totally depleted before $v_{\alpha,c}(y)$ leaves a small
neighborhood of the initial point. Thus $v_{\alpha,c}$ remains close to a solution of the
linear equation $v'' + cv' = 0$, hence converges to a nonzero limit $v_\infty$ as
$y \to +\infty$. In particular, we have $T(\alpha,c) = +\infty$ if $\alpha > 0$ is large
enough. We leave the details to the reader.
\end{proof}
The rest of the proof of Theorem~\ref{main2} follows the arguments given in
Sections~\ref{subsec24}--\ref{subsec26} without substantial modifications. In particular,
Lemma~\ref{lem:limits} is unchanged, so that we can define $\alpha_1(c)$ as in
\eqref{alpha1def}, and the analogue of Lemma~\ref{lem:alpha1} asserts that
$-\infty < \alpha_1(c) < +\infty$ for any $c > 0$. If $\alpha = \alpha_1(c)$, we have
$T(\alpha,c) = +\infty$ and $u_\infty(\alpha,c) = 1$ as in Remark~\ref{rem:alpha1}, and
finally $v_\infty(\alpha,c) = 0$ because the analysis on the center manifold of the healthy
state, which is given in Section~\ref{subsec25}, does not depend on the value of the
parameter $d > 1$. This proves the existence of a (unique) heteroclinic trajectory of
system~\eqref{Ode3} connecting the coexistence state $S_d$ to the healthy state $S_+$,
when $0 < d < 1$.
When returning to the original variables, we have to keep
in mind that the change of variables \eqref{xidef} is not
close to identity for large negative values of $y$, because
$u(y) \to 1-d$ as $y \to -\infty$. Instead of \eqref{xiexp}, we
thus define
\[
\xi(y) \,=\, \Phi^{-1}(y) \,=\, dy - \int_{-\infty}^y
\Bigl(u(y') + d -1\Bigr)\,{\rm d} y'\,, \qquad y \in \mathbb{R}\,,
\]
and we observe that the function $\Phi$ satisfies\thinspace :
\[
\Phi(\xi) \,=\, \begin{cases}
\frac{1}{d}\,\xi + \mathcal{O}\Bigl(e^{\eta\xi/d}\Bigr)
& \hbox{as} \quad \xi \to -\infty\,, \\
e^{\gamma(\xi-\xi_0)} + \mathcal{O}(1)
& \hbox{as} \quad \xi \to +\infty\,, \\
\end{cases}
\]
where $\xi_0 \in \mathbb{R}$, $\gamma = r/c$, and $\eta = \min(\mu,\lambda)$.
Setting $\mathcal{U}(\xi) = u(\Phi(\xi))$, $\mathcal{V}(\xi) = v(\Phi(\xi))$, we
obtain the desired solution of \eqref{Ode1} satisfying the boundary
conditions \eqref{BC2}. Note that
\begin{align*}
\mathcal{U}(\xi) \,&=\, 1 - d + \alpha e^{\mu \xi/d} + \frac{d\mu}{\mu-\lambda}
\Bigl(e^{\lambda \xi/d} - e^{\mu \xi/d}\Bigr) + \mathcal{O}\Bigl(e^{2\eta\xi/d}
\Bigr)\,, \\
\mathcal{V}(\xi) \,&=\, 1 - e^{\lambda \xi/d} + \mathcal{O}\Bigl(e^{(\lambda+\eta)\xi/d}
\Bigr)\,, \qquad \hbox{as }\xi \to -\infty\,,
\end{align*}
for some $\alpha \in \mathbb{R}$, whereas the asymptotic behavior
\eqref{AsymUV2} as $\xi \to +\infty$ is unchanged. This concludes
the proof of Theorem~\ref{main2}. \mathbb{Q}ED
\section{Asymptotic analysis of slowly propagating fronts}\label{sec3}
Perhaps the most striking aspect of Theorems~\ref{main1} and \ref{main2} is the
absence of a minimal speed for the monotone traveling waves of
system~\eqref{redGGsys}. To understand what happens in the singular limit
$c \to 0$, we compute in this section the leading term of a (formal) asymptotic
expansion of the front profile. We do not feel the necessity of rigorous proofs
at this stage, but we provide numerical illustrations supporting our
arguments. We always assume that $d > 1$, and we consider propagation fronts
connecting the infected state $(\mathcal{U}_-,\mathcal{V}_-) = (0,1)$ and the healthy state
$(\mathcal{U}_+,\mathcal{V}_+) = (1,0)$ of system~\eqref{Ode1}. As is explained in
Section~\ref{sec2}, such fronts correspond to solutions $(u,v,w)$ of the
desingularized system \eqref{Ode3} satisfying the asymptotic conditions \eqref{BC3}.
If the parameter $c > 0$ is very small, the first equation in \eqref{Ode3} suggests
that the function $u$ is a {\em fast variable} in the sense of geometric singular
perturbation theory \cite{Fen79}. Its transition from the initial value $0$ to the
final value $1$ should occur in a small interval of size $\mathcal{O}(c)$ centered at some
point $y \in \mathbb{R}$, which we assume to be the origin $y = 0$. So, in a first approximation,
we expect that the function $v$ is close to a function $v_0$ satisfying
\begin{equation}\label{v0def}
\begin{array}{lll}
v_0''(y) + c\,v_0'(y) + r v_0(y)\bigl(1-v_0(y)\bigr) \,=\, 0\,,
& \hbox{ if} & y < 0\,, \\[1mm]
v_0''(y) + c\,v_0'(y) \,=\, 0\,, & \hbox{ if} & y > 0\,.
\end{array}
\end{equation}
\begin{lem}\label{lem:v0}
If $0 < c < 2\sqrt{r}$, there exists a unique decreasing function $v_0 : \mathbb{R} \to
(0,1)$ of class $C^{1,1}$ satisfying Eq.~\eqref{v0def} as well as the boundary
conditions $v_0(-\infty) = 1$, $v_0(+\infty) = 0$. Moreover, one has
\begin{equation}\label{v00}
v_0(0) \,=\, 1 - \frac{c}{c+\lambda} + \mathcal{O}(c^2)\,, \qquad \hbox{as }~
c \to 0\,,
\end{equation}
where $\lambda$ is given by \eqref{lamudef}.
\end{lem}
\begin{proof}
Let $\phi$ be a decreasing solution of the Fisher--KPP equation \eqref{FKPP} such
that $\phi(y) \to 1$ as $y \to -\infty$. Since $c < 2\sqrt{r}$, we know that
$\phi$ does not stay positive, so there exists a unique $y_0 \in \mathbb{R}$ such that
$\phi(y_0) = 0$ and $\phi(y) > 0$ for all $y < y_0$.
We next consider the smooth function $\psi : (-\infty,y_0] \to \mathbb{R}$ defined by
$\psi(y) = \phi'(y) + c\phi(y)$. We have $\psi'(y) = -r\phi(y)(1-\phi(y)) < 0$
for all $y < y_0$, whereas $\psi(-\infty) = c > 0$ and $\psi(y_0) = \phi'(y_0) < 0$.
So there exists a unique $y_1 < y_0$ such that $\psi(y_1) = 0$, and after
a suitable translation of the variable $y$ we can assume that $y_1 = 0$.
If we now define
\begin{equation}\label{v0exp}
v_0(y) \,=\, \begin{cases} \phi(y) & \hbox{if } y \le 0\,,\\
\phi(0)e^{-cy} & \hbox{if } y \ge 0\,,
\end{cases}
\end{equation}
we see that $v_0 \in C^{1,1}(\mathbb{R})$, because $\phi'(0) + c\phi(0) = \psi(0) = 0$,
and that $v_0$ satisfies \eqref{v0def} together with the desired boundary conditions.
Finally, we have as in \eqref{asym1}
\begin{equation*}
v(y) \,=\, 1 - e^{\lambda (y+y_2)} + \mathcal{O}\Bigl(e^{2\lambda(y+y_2)}\Bigr)\,,
\qquad \hbox{as }~ y \to -\infty\,,
\end{equation*}
for some translation parameter $y_2 \in \mathbb{R}$. Neglecting the higher order
terms, we obtain the relation $0 = v'(0) + cv(0) = c - (c+\lambda)e^{\lambda y_2}$
which determines $y_2$, and we arrive at \eqref{v00}.
\end{proof}
\begin{rem}\label{rem:v0}
There is no explicit formula for the function $v_0$ in Lemma~\ref{lem:v0},
but in the asymptotic regime where $c \ll 1$ one has $v_0 = \hat v_0 +
\mathcal{O}(c^2)$ where
\begin{equation}\label{v0hat}
\hat v_0(y) \,=\, \begin{cases} 1 - {{\rm d}S\frac{c}{c+\lambda}}
\,e^{\lambda y} & \hbox{if } y \le 0\,,\\[2mm]
{{\rm d}S\frac{\lambda}{c+\lambda}}\,e^{-cy} & \hbox{if } y \ge 0\,.
\end{cases}
\end{equation}
Note that $\hat v_0 \in C^{1,1}(\mathbb{R})$ and $\hat v_0(-\infty) = 1$,
$\hat v_0(+\infty) = 0$.
\end{rem}
We next construct the leading order approximation of the function $u$.
We assume that $c > 0$ is small enough so that $v_0(0) > 1/d$, which
is possible in view of \eqref{v00}, and we denote $b = d v_0(0) - 1 > 0$.
Observing that $dv_0(y) \approx dv_0(0) = 1 + b$ if $|y| = \mathcal{O}(c)$, we
postulate that $u$ is well approximated by a function $u_0$ satisfying
the simplified equation
\begin{equation}\label{u0eq}
u_0'(y) \,=\, \frac{1}{c}\,u_0(y)(1-u_0(y))\bigl(b + u_0(y)\bigr)\,,
\qquad y \in \mathbb{R}\,,
\end{equation}
together with the boundary conditions $u_0(-\infty) = 0$, $u_0(+\infty) = 1$.
The solution of \eqref{u0eq} is implicitly given by the relation
\begin{equation}\label{u0exp}
\frac{u_0(y)^{1+b}}{\bigl(1-u_0(y)\bigr)^b \bigl(b + u_0(y)\bigr)}
\,=\, \frac{\alpha^{1+b}}{b}\,\exp\biggl(\frac{b(1+b)}{c}\,y\biggr)\,,
\qquad y \in \mathbb{R}\,,
\end{equation}
where $\alpha > 0$ is an integration constant which amounts to fixing the
value $u_0(0) \in (0,1)$. This constant can be determined, for instance, by
imposing the relation
\begin{equation}\label{capp}
c \,=\, r \int_{\mathbb{R}} \hat v_0(y)\bigl(1 - \hat v_0(y)\bigr)
\bigl(1 - u_0(y)\bigr)\,{\rm d} y\,,
\end{equation}
which is the analogue of \eqref{cformula} at our level of approximation.
For later use, we also note that $u_0(y) = \alpha\,e^{by/c} + \mathcal{O}(e^{2by/c})$
in the asymptotic regime where $y \to -\infty$.
The approximate solution $(u_0,v_0)$ of \eqref{Ode2} constructed so
far describes relatively well the asymptotic region $y \to -\infty$
and the central region where the transition occurs from a neighborhood
of $(0,1)$ to the vicinity of $(1,0)$. However, this first-order
approximation is not realistic when $y > 0$ is large, because
$1-u_0(y)$ and $v_0(y)$ decay exponentially to zero as $y \to +\infty$,
in sharp contrast with \eqref{asym2}. Nevertheless, it is highly interesting
at this point to return to the original variables and to compute the
corresponding approximate solution $(\mathcal{U}_0,\mathcal{V}_0)$ of \eqref{Ode1}.
First of all, it is important to realize that $(\mathcal{U}_0,\mathcal{V}_0)$ is
a {\em sharp front}, associated with some finite value $\bar\xi < +\infty$.
Indeed, in view of \eqref{u0eq} the change of variables \eqref{xidef} becomes
\begin{equation}\label{chang1}
\frac{{\rm d} \xi}{{\rm d} y} \,=\, 1 - u_0(y) \,=\, \frac{c u_0'(y)}{
u_0(y)(b+u_0(y))}\,, \qquad y \in \mathbb{R}\,,
\end{equation}
so that
\begin{equation}\label{xiapp}
\xi \,=\, \Phi^{-1}(y) \,=\, \frac{c}{b}\,\log\biggl(\frac{(1{+}b)
u_0(y)}{b+u_0(y)}\biggr)\,, \qquad y \in \mathbb{R}\,.
\end{equation}
Here we have normalized things so that $\bar\xi = 0$, which means that the map
$\Phi : (-\infty,0) \to \mathbb{R}$ is a diffeomorphism. Moreover $\Phi^{-1}(y)
\approx y + \kappa$ as $y \to -\infty$, where $\kappa = \frac{c}{b}\log\bigl(
\frac{1+b}{b}\,\alpha\bigr)$. It follows immediately from \eqref{xiapp} that
\begin{equation}\label{U0exp}
\mathcal{U}_0(\xi) \,:=\, u_0(\Phi(\xi)) \,=\, \frac{b\,e^{b\xi/c}}{1+b -
e^{b\xi/c}}\,, \qquad \xi \in (-\infty,0)\,.
\end{equation}
Remarkably, this expression does not involve the constant $\alpha$ in \eqref{u0exp}.
Using \eqref{U0exp}, we can in turn compute the map $\Phi$ more explicitly. To
this end, we write \eqref{chang1} in the equivalent form
\begin{equation}\label{chang2}
\frac{{\rm d} y}{{\rm d} \xi} \,=\, \frac{1}{1 - \mathcal{U}_0(\xi)} \,=\, \frac{1}{1+b}
\,\frac{1+b - e^{b\xi/c}}{1 - e^{b\xi/c}}\,, \qquad \xi \in (-\infty,0)\,,
\end{equation}
and we easily deduce
\begin{equation}\label{Phiapp}
y \,=\, \Phi(\xi) \,=\, \xi - \frac{c}{1+b}\,\log\Bigl(1 - e^{b\xi/c}\Bigr)
- \kappa\,, \qquad \xi \in (-\infty,0)\,.
\end{equation}
It follows that
\begin{equation}\label{V0exp}
\mathcal{V}_0(\xi) \,:=\, \hat v_0(\Phi(\xi)) \,=\, \begin{cases}
1 - {{\rm d}S\frac{c}{c+\lambda}}\,e^{\lambda\Phi(\xi)} & \hbox{if } \xi \le \xi_*\,,\\[2mm]
{{\rm d}S\frac{\lambda}{c+\lambda}}\,e^{-c\Phi(\xi)} & \hbox{if } \xi_* \le \xi < 0\,,
\end{cases}
\end{equation}
where $\xi_* = \Phi^{-1}(0) \in (-\infty,0)$. Note that $\xi_*$ depends on
$\kappa$, hence on the constant $\alpha$ in \eqref{u0exp}. Figure~\ref{fig4}
shows that the approximations \eqref{U0exp}, \eqref{V0exp} are remarkably
accurate, even at moderately small speeds such as $c = 0.2$.
\begin{figure}
\caption{{\small The sharp profile of the propagation front $(\mathcal{U}
\label{fig4}
\end{figure}
Let $\phi_0 : (0,1) \to (0,1)$ be the approximate diffusion coefficient defined
by
\begin{equation}\label{Deff2}
1 - \mathcal{U}_0(\xi) \,=\, \phi_0\bigl(\mathcal{V}_0(\xi)\bigr)\,, \qquad \xi \in (-\infty,0)\,.
\end{equation}
Equivalently, we have $1 - u_0(y) = \phi_0(\hat v_0(y))$ for all $y \in \mathbb{R}$.
The function $\phi_0$ can be evaluated using the formulas \eqref{U0exp}, \eqref{V0exp},
and is expected to give a good approximation of the effective diffusion coefficient
\eqref{Deff} when $c \ll 1$. It is straightforward to verify that
\begin{equation}\label{Dasym}
\phi_0(v) \,\approx\, \beta \biggl(\frac{c+\lambda}{\lambda}\,v\biggr)^{\frac{1+b}{c^2}}
\quad \hbox{as } v \to 0\,, \qquad \hbox{where}\quad \beta^b \,=\,
\frac{b}{b+1}\,\frac{1}{\alpha^{1+b}}\,.
\end{equation}
Since $1+b = d + \mathcal{O}(c)$, this means that the exponent $(1+b)/c^2$ in
\eqref{Dasym} is very large when $c \ll 1$, so that the function $\phi_0$ is
extremely flat near the origin, see Figure~\ref{fig4}b. This in turn
explains why Theorem~\ref{main1} does not conflict with classical results
establishing the existence of a minimal speed for the traveling waves of
scalar equations with degenerate diffusion. To see this, consider the
model equation
\begin{equation}\label{Dm}
\partial_t V \,=\, D\,\partial_x \bigl(V^m \partial_x V\bigr) +
r V (1 - V)\,,
\end{equation}
where $D,r$ are positive constants and $m \in \mathbb{N}\setminus\{0\}$. It is known
\cite{AtkiReutRidl81} that the minimal speed $c_*$ of the traveling waves
for \eqref{Dm} satisfies
\[
\frac{2Dr}{(m+1)(m+2)} \,\le\, c_* \,\le\, \frac{2Dr}{m(m+1)}\,,
\]
so that $c_* \sim \sqrt{2Dr}/m$ as $m \to +\infty$. Although \eqref{Dasym} is
only an asymptotic formula valid for $v \to 0$, this suggests that the minimal
speed for the scalar equation \eqref{GGscalar} where $\phi = \phi_0$ can be
compared to the minimal speed for \eqref{Dm} where $m = (1+b)/c^2$. The
latter is proportional to $1/m \approx c^2/d$, and should therefore become
smaller than $c$ when $c \ll 1$. Summarizing, given any $c > 0$ (no matter how
small), the effective diffusion coefficient $\phi$ defined by \eqref{Deff} is so
flat near the origin that the minimal speed $c_*$ associated with the scalar
equation \eqref{GGscalar} always satisfies $c_* \le c$.
\section{Conclusions and perspectives}\label{sec4}
We conclude this paper with a list of possible questions
that are, in our opinion, worth investigating in the future.
\subsection{External parameters $d$ and $r$}\label{subsec41}
Tumor growth is dependent on the complex interactive dynamics of many different
factors, including competitive effects (here, described by the parameter $d$)
and growth factors (here, by the parameter $r$). Invasion fronts for the reduced
Gatenby--Gawlinski model \eqref{redGGsys} have been explored in detail,
providing a complete existence result for all positive values of $d$ and
$r$. The critical threshold $d=1$ separates two different scenarios
(heterogeneous versus homogeneous invasion) with a bifurcation appearing already
at the level of the equilibria. In contrast, varying $r$ does not lead to
qualitatively different behaviors. These parameters are both relevant from an
``oncological'' point of view, as they describe two distinct properties of the
system: increasing $d$ enhances the competitivity of the cancerous cells against
the healthy tissue, while $r$ describes the reproduction activity of the tumor
cells alone. In principle, one should be able to fix appropriate values for these
parameters by comparing the shape of the propagation fronts of \eqref{redGGsys}
with experimental data or predictions from more complete models.
\subsection{Stability and minimal speed}\label{subsec42}
While our results prove the existence of propagation fronts for any positive
value of the speed parameter $c$, this does not mean that there is no
minimal speed for system~\eqref{redGGsys}. First, we do not have any information
so far on the stability of the fronts constructed in Theorems~\ref{main1}
and \ref{main2}. In fact, there are even mathematical issues concerning the
Cauchy problem itself, see Section~\ref{subsec43} below. So, it may well be
that the propagation fronts of system~\eqref{redGGsys} are unstable in some
parameter regimes, for instance when $c > 0$ is sufficiently small. Also,
we do not know which propagation front is selected from Heaviside-type
initial data, and it is therefore conceivable that a minimal speed arises
in that context too. This last equation is of course much more difficult
than in the scalar case, as system~\eqref{redGGsys} has no maximum principle.
\subsection{Well-posedness of the Cauchy problem}\label{subsec43}
Due to the presence of degeneracy in the second equation of \eqref{redGGsys},
establishing the well-posedness of the Cauchy problem on the real line $\mathbb{R}$
is a delicate issue. The crucial question is of course whether the threshold
value $\bar U$ such that $f(\bar U)=0$ (in our case, $\bar U=1$) is reached
somewhere. In that case, heuristic arguments suggest that the problem is not
well-posed in the classical sense, so that some appropriate weak formulation has
to be used. It happens that our reduction from \eqref{GGsys} to
\eqref{redGGsys}, which eliminates the intermediate agent $W$, drastically
increases the stiffness of the diffusion degeneracy. In particular, if $V=0$ and
$U\equiv 1$ in some region, i.e. tumor cells are absent and healthy tissue is at
carrying capacity, propagation is expected to be completely blocked, thus
preventing any invasion mechanism. To our knowledge, well-posedness in some appropriate
weak framework has not been explored yet, but partial results can be found in
\cite{BarrNurn02, BarrDeck12}. Of course if the critical value $\bar U = 1$
is never reached, existence of a unique classical solution is expected, and
can be proved by standard techniques.
On the other hand, an extended version of the Gatenby-Gawlinski model (see
\cite{McGiEtAl14}) has been analyzed in \cite{TaoTell16} for the case of a
multi-dimensional bounded domain with smooth boundary and zero-flux boundary
conditions. In view of the correspondence \eqref{redGGgenGG}, the assumptions in
\cite{TaoTell16} reduce, in the case of \eqref{redGGsys}, to the single hypothesis
$d<1$, which corresponds to heterogeneous invasion. Under such conditions, it
can be proved that, for any positive time $t$, the component $U$ is bounded away
from the critical value $1$, so that the problem possesses a unique classical
solution for initial data $U_0\in(0,1)$ and $V_0>0$. Incidentally, let us remark
that the assumption that $V_0 > 0$ corresponds to the initial presence of tumor
spread everywhere in the healthy tissue, which is clearly questionable from a
biological perspective. A different approach has been proposed in
\cite{MarkMeraSuru13}, where the authors show local and global existence
invoking an iterative strategy. This approach imposes no restriction on the
values of the coupling parameter $d$, but it is crucial to assume that
$U_0\leq \theta$ for some $\theta < 1$. Summarizing, the fundamental question of
well-posedness for system \eqref{redGGsys} remains currently unsolved in its
full generality.
Ideally, the target is to come back to the complete Gatenby--Gawlinski model
\eqref{GGsys}. Actually, the results quoted above
\cite{MarkMeraSuru13,TaoTell16} do apply to system \eqref{GGsys}. The mediation of
the acid variable --satisfying a linear parabolic equation with dissipation and
external forcing-- increases the possibility of recovering some sort of
classical framework, even if we cannot quote any result of this nature.
Some weak formulation may also be needed to prove well-posedness in the
sense of Hadamard --i.e. existence, uniqueness and continuous dependence--,
but we are not aware of any complete result in that direction either.
\subsection{Propagating fronts for the complete model}\label{subsec44}
A comprehensive study of existence of traveling waves for the original
Gatenby--Gawlinski model \eqref{GGsys} is currently not available in the
literature. Some partial results, based on singular perturbation theory,
have been presented in \cite{DaviEtAl18}. In any case, there is a clear
computational evidence of existence of such fronts, see
\cite{McGiEtAl14,MoscSime19}. In addition, numerical simulations for
\eqref{GGsys} indicate that the coupling with the acid equation is crucial
for the existence of a strictly positive minimal speed, which should
correspond to a sharp front in the regime $d>1$. As a final remark, let us
observe that many properties used in the present work --for example, the
monotonicity in Lemma~\ref{lem:monotone}-- are specific to the reduced model
\eqref{redGGsys} and cannot be easily generalized to the original
Gatenby--Gawlinski system \eqref{GGsys}.
{\small
}
\end{document} | math |
- शहर में और महंगी हो गई प्रॉपर्टी, गाज़ियाबाद न्यूज इन हिन्दी -अमर उजाला बेहतर अनुभव के लिए अपनी सेटिंग्स में जाकर हाई मोड चुनें।
गाज़ियाबाद शहर में और महंगी हो गई प्रॉपर्टी
लागू हुए प्रस्तावित डीएम सर्किल रेट की बढ़ोतरी गाजियाबाद। शहर में प्रॉपर्टी के दामों में जबर्दस्त उछाल आ गया है। शनिवार को शहर में नए डीएम सर्किल रेट लागू हो गए हैं। डीएम ने सर्किल रेट बढ़ाने के प्रस्ताव को मंजूरी दे दी है। जिला प्रशासन के इस फैसले के बाद कौशांबी सबसे मंहगी कालोनी हो गई है। यहां का डीएम सर्किल रेट ५५ हजार रुपये प्रतिवर्गमीटर हो गया है। डीएम सर्किल रेट बढ़ने से जीडीए की कालोनियों के सेक्टर रेट भी बढ़ गए हैं।शहर की जमीनों के सर्किल रेट बढ़ाने के लिए आईजी स्टांप ने प्रस्तावित रेट को ३१ मई तक तैयार करने के निर्देश दिए थे। हालांकि २५ मई से निकाय चुनाव की आचार संहिता लागू हो जाने के कारण मामला ठंडे बस्ते में चला गया था। इसी बीच मुख्य सचिव जावेद उस्मानी ने डीएम और मेरठ मंडलायुक्त को पत्र लिखकर चुनाव बाद डीएम सर्किल रेट बढ़ाने के निर्देश दिए थे। शासन के निर्देशों के क्रम में शनिवार को बढ़ोतरी लागू की गई है। सर्किल रेट में १० से ७५ फीसदी के बीच बढ़ोतरी की गई है। राज नगर के रेट २० हजार से बढ़कर ३६ हजार रुपये प्रति वर्गमीटर हो गए हैं। एआईजी स्टांप केपी यादव ने बताया कि डीएम ने नए सर्किल रेट लागू करने पर सहमति दे दी है। | hindi |
Forbes doesn’t name a single woman among Canada’s 45 billionaires.
There’s more to helping the world beyond putting on a suit.
Who said dubstep was dead?
Cymbal might have the answer—with help from Spotify and SoundCloud's libraries.
The annual report from IMS shows flatlining record sales and moderate gains in streaming while the live sector holds steady.
The dating app's biggest stakeholder, InterActiveCorp (also known as IAC), is looking for an "Eric Schmidt-like person" to replace the 28-year-old, who's had a year marked by business triumphs and personal tribulations.
Who Are This Year’s Lowest Paid DJs?
You've seen the tops, now see the trots.
According to FORBES, Calvin is the most powerful DJ in the world. Here's how he reached the top. | english |
using System;
using Microsoft.Extensions.Configuration;
using Microsoft.Extensions.Logging;
using Microsoft.Extensions.Primitives;
namespace Logging.Memory.Settings
{
/// <summary>
/// IConfiguration IMemoryLoggerSettings realization
/// </summary>
public class ConfigurationMemoryLoggerSettings : IMemoryLoggerSettings
{
private const int DefaultMaxLogCount = 200;
private readonly IConfiguration _configuration;
/// <summary>
/// constractor
/// </summary>
public ConfigurationMemoryLoggerSettings(IConfiguration configuration)
{
_configuration = configuration;
ChangeToken = configuration.GetReloadToken();
}
#region IMemoryLoggerSettings implementation
/// <inheritdoc />
public IChangeToken ChangeToken { get; private set; }
/// <inheritdoc />
public int MaxLogCount
{
get
{
int maxLogCount;
var value = _configuration["MaxLogCount"];
if (string.IsNullOrEmpty(value))
{
return DefaultMaxLogCount;
}
else if (int.TryParse(value, out maxLogCount))
{
return maxLogCount;
}
else
{
throw new InvalidOperationException($"Configuration value '{value}' for setting '{nameof(MaxLogCount)}' is not supported.");
}
}
}
/// <inheritdoc />
public IMemoryLoggerSettings Reload()
{
ChangeToken = null;
return new ConfigurationMemoryLoggerSettings(_configuration);
}
/// <inheritdoc />
public bool TryGetSwitch(string name, out LogLevel level)
{
var switches = _configuration.GetSection("LogLevel");
if (switches == null)
{
level = LogLevel.None;
return false;
}
var value = switches[name];
if (string.IsNullOrEmpty(value))
{
level = LogLevel.None;
return false;
}
else if (Enum.TryParse<LogLevel>(value, out level))
{
return true;
}
else
{
var message = $"Configuration value '{value}' for category '{name}' is not supported.";
throw new InvalidOperationException(message);
}
}
#endregion
}
}
| code |
---
title: "Noticias breves"
header:
overlay_image: /img/NotiEnBlancoV2.jpg
layout: single
categories:
- 'Persona 3 FES'
- 'Ace Combat 3: Electrosphere'
- 'Policenauts'
- 'Broken Sword 2.5'
tags:
- 'Persona 3 FES'
- 'Ace Combat 3: Electrosphere'
- 'Policenauts'
- 'Broken Sword 2.5'
---
Saludos. Hoy quiero traer algunas noticias breves sobre el estado de mis proyectos abiertos.
- Persona 3 FES sigue en proceso de revisión previa al testeo. La revisión es lenta, aunque no debería ser tan lenta como la traducción, así que nos tomaremos el tiempo que sea necesario para que todo quede limpio.
- Policenauts sigue en su situación anterior. Recapitulando, he encontrado a un nuevo programador que me está ayudando con las herramientas, Kaplas, que ha estado arreglando y terminando el programa para editar los subtítulos en los vídeos de la versión de PlayStation. La herramienta está casi acabada, pero a diferencia de otros afortunados por el COVID-19, él ha estado cargadito de trabajo, así que no hay muchos avances.
- Broken Sword 2.5 está parado porque ha habido problemas con uno de los actores, que hacía a uno de los personajes que aparecían en los juegos originales, lo que me ha llevado a tener que montar otra vez casting. Va a llevar un tiempo.
- Y dejo lo mejor para el final: Ace Combat 3 ha pegado un buen estirón desde la última vez que hablé de él en profundidad:
- Se ha terminado la retraducción preliminar, literal y acotada al inglés con la que estamos trabajando los equipos italiano y español. Ahora la traducción inglesa tendrá que pasar por un proceso de edición, revisión y adaptación.
- La traducción española está a la par que la inglesa, es decir, **los textos están traducidos al 100%**, pero falta darles una buena revisión, ya que al haber ido traduciendo por tandas en un espacio de año y pico, hay fallos de consistencia.
- La parte de programación también ha pegado un estirón: La herramienta que necesitábamos para importar los textos de vuelta al juego (en este caso, convertir textos a gráficos) ha avanzado lo suficiente como para poder reimportar todos los subtítulos del juego (que son los que utilizan este formato). Ahora mismo quedarían por pulir algunas cosas de este programa y hacer uno nuevo para editar los videocorreos del Data Swallow (en concreto, la entrevista con Rena, ya que tiene textos sobreimpuestos).
Por desgracia, no puedo mostrar capturas nuevas de Ace Combat 3, no hasta tener la revisión en un estado algo avanzado.
Y eso es todo por ahora. Os deseo lo mejor en estos tiempos tan revueltos.
Seguiremos informando. | code |
Tying a design all together with unique accessories is accomplished through experience and wide variety of resources. Those resources are ever expanding as we love to seek and uncover unique and undiscovered treasures. We also offer Custom Upholstery Services and a wide range of specialty items including Tapestries and Area Rugs. | english |
होम सिटी & स्टेट्स यूजीसी नेट में फिर छात्राओं ने बाजी मारी
यूजीसी नेट में फिर छात्राओं ने बाजी मारी
चंडीगढ़। कालेज और यूनिवर्सिटी में असिस्टेंट प्रोफेसर के लिए अनिवार्य यूजीसी नेट में ट्राइसिटी के होनहारों का दबदबा जारी है। दिसंबर २०१२ में यूजीसी नेट में पंजाब यूनिवर्सिटी सेंटर से अपीयर होने वाले ९३८ युवाओं ने यूजीसी नेट और जेआरएफ क्लीयर कर लिया है। देशभर में नेट का पास प्रतिशत ६.३७ रहा, जबकि ट्राइसिटी का ४.६9 प्रतिशत। ८५८ ने यूजीसी नेट और ८० ने जेआरएफ (जूनियर रिसर्च फैलोशिप) में सफलता हासिल की है। पीयू सेंटर से २० हजार युवा अपीयर हुए थे और नेट में इस बार भी ९० फीसदी छात्राएं ही सफल रहीं।
सेक्टर-१५ की ब्राइट एकेडमी के डायरेक्टर आरके महाजन ने कहा कि इस बार का रिजल्ट उम्मीद से काफी बेहतर रहा है। उनके ७५ स्टूडेंट्स ने नेट क्लीयर किया है। यूजीसी नेट में मैनेजमेंट विषय में सबसे अधिक २१४ ने नेट और २४ ने जेएफआर क्लीयर किया है।
जून २०१२ से कम पास प्रतिशत
यूजीसी नेट में हर बार पीयू का औसत पास प्रतिशत काफी बेहतर रहता है। दिसंबर २०११ में ५२४ (३९५ नेट, १२९ जेआरएफ) जून २०१२ में ११६४ (१०५३ नेट, १११ जेआरएफ) ने पास किया है। यूजीसी नेट में तीनों पेपर आब्जेक्टिव आने से पास प्रतिशत बढ़ा है। उधर, देशभर में दिसंबर २०१२ में आयोजित नेट में ३६६९ ने जेआरएफ और ३५५५७ ने नेट क्लीयर किया है।
किस विषय में कितने उत्तीर्ण
विषय नेट जेआरएफ
मैनेजमेंट २१४ २४
कामर्स १५७ ९
इकोनामिक्स २१ कोई नहीं
एजूकेशन ८५ ३
इंग्लिश १५ २
कंप्यूटर साइंस ४० ४
पंजाबी ३७ ८
लॉ ५० ५
मास कम्यूनिकेशन ५ १
यूजीसी नेट का रिजल्ट काफी बेहतर रहा है। आब्जेक्टिव पेपर आने से विद्यार्थियों को काफी फायदा मिला है। कामर्स और मैनेजमेंट विषयों का रिजल्ट बेहतर है।
- आरके महाजन, डायरेक्टर, ब्राइट एकेडमी, सेक्टर-१५ चंडीगढ़ | hindi |
We work with Epstein-Barr Virus (EBV) because it causes several different cancers in people. EBV is a herpesvirus that causes the common, benign infectious mononucleosis, as well as lymphomas such as Burkitt's Lymphoma, most B-cell lymphomas in immunocompromised hosts, and carcinomas such as nasopharyngeal carcinoma. We study EBV both to understand its contributions to these diseases molecularly and to develop rational means to treat them.
Our research focuses on two facets of EBV pivotal to its inducing and maintaining human tumors. One gene product of EBV, LMP1, mimics cellular signaling pathways but in a ligand-independent manner. Its signaling drives proliferation of EBV-infected B-cells, but at high levels inhibits that proliferation. We are dissecting the mechanisms by which LMP1 regulates its host cell both positively and negatively. A second gene product of EBV, EBNA1, binds several elements of EBV's origin of plasmid synthesis, oriP, to mediate the synthesis and maintenance of the viral replicon in proliferating cells. EBV's replicon replicates once per S-phase and uses the cell's DNA synthetic machinery to do so. We study EBNA1 and oriP to elucidate the mechanisms by which EBV DNA is synthesized and segregated to daughter cells. We also study this viral replicon to gain insights into how EBV subverts its host's synthetic machinery to support extrachromosomal DNA synthesis. Finally we are studying EBNA1 which not only mediates replication of EBV's replicon, but also inhibits apoptosis in infectious B-cells to understand its roles in supporting survival of EBV-associated tumors. We want to target EBNA1's survival functions to develop treatments for tumors caused by EBV.
Yang YC, Liem A, Lambert PF, Sugden B. Dissecting the regulation of EBV's BART miRNAs in carcinomas. Virology. 2017 Mar 1;505:148-154. doi: 10.1016/j.virol.2017.02.013. PubMed PMID: 28259048; PubMed Central PMCID: PMC5504693.
Albanese M, Tagawa T, Bouvet M, Maliqi L, Lutter D, Hoser J, Hastreiter M, Hayes M, Sugden B, Martin L, Moosmann A, Hammerschmidt W. Epstein-Barr virus microRNAs reduce immune surveillance by virus-specific CD8+ T cells. Proc Natl Acad Sci U S A. 2016 Oct 18;113(42):E6467-E6475. PubMed PMID: 27698133.; PubMed Central PMCID: PMC5081573.
Shrestha, P., and Sugden, B. Identification of Properties of the Kaposi’s Sarcoma-Associated Herpesvirus Latent Origin of Replication That Are Essential for the Efficient Establishment and Maintenance of Intact Plasmids. J. Virol., 88(15): 8490-8503, 2014. | english |
ژنہوا نیوز ایجنسی ہٕنٛدِ رپورٹَس مُطٲبِق چھُ خیال یِوان کرنہٕ زِ نار لوٚگ بجلی کہِ خرٲبی سٟتؠ | kashmiri |
/*
* Copyright (c) 2008-2020, Hazelcast, Inc. All Rights Reserved.
*
* Licensed under the Apache License, Version 2.0 (the "License");
* you may not use this file except in compliance with the License.
* You may obtain a copy of the License at
*
* http://www.apache.org/licenses/LICENSE-2.0
*
* Unless required by applicable law or agreed to in writing, software
* distributed under the License is distributed on an "AS IS" BASIS,
* WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
* See the License for the specific language governing permissions and
* limitations under the License.
*/
package com.hazelcast.multimap.impl.txn;
import com.hazelcast.core.EntryEventType;
import com.hazelcast.internal.nio.IOUtil;
import com.hazelcast.multimap.impl.MultiMapContainer;
import com.hazelcast.multimap.impl.MultiMapDataSerializerHook;
import com.hazelcast.multimap.impl.MultiMapRecord;
import com.hazelcast.multimap.impl.MultiMapService;
import com.hazelcast.multimap.impl.MultiMapValue;
import com.hazelcast.multimap.impl.operations.AbstractKeyBasedMultiMapOperation;
import com.hazelcast.nio.ObjectDataInput;
import com.hazelcast.nio.ObjectDataOutput;
import com.hazelcast.internal.serialization.Data;
import com.hazelcast.spi.impl.operationservice.BackupAwareOperation;
import com.hazelcast.spi.impl.operationservice.Operation;
import com.hazelcast.spi.impl.operationservice.MutatingOperation;
import java.io.IOException;
import java.util.Collection;
public class TxnPutOperation extends AbstractKeyBasedMultiMapOperation implements BackupAwareOperation, MutatingOperation {
private long recordId;
private Data value;
private transient long startTimeNanos;
public TxnPutOperation() {
}
public TxnPutOperation(String name, Data dataKey, Data value, long recordId) {
super(name, dataKey);
this.recordId = recordId;
this.value = value;
}
@Override
public void run() throws Exception {
startTimeNanos = System.nanoTime();
MultiMapContainer container = getOrCreateContainer();
MultiMapValue multiMapValue = container.getOrCreateMultiMapValue(dataKey);
if (multiMapValue.containsRecordId(recordId)) {
response = false;
return;
}
response = true;
container.update();
Collection<MultiMapRecord> coll = multiMapValue.getCollection(false);
MultiMapRecord record = new MultiMapRecord(recordId, isBinary() ? value : toObject(value));
coll.add(record);
}
@Override
public void afterRun() throws Exception {
long elapsed = Math.max(0, System.nanoTime() - startTimeNanos);
MultiMapService service = getService();
service.getLocalMultiMapStatsImpl(name).incrementPutLatencyNanos(elapsed);
if (Boolean.TRUE.equals(response)) {
publishEvent(EntryEventType.ADDED, dataKey, value, null);
}
}
public long getRecordId() {
return recordId;
}
@Override
public boolean shouldBackup() {
return Boolean.TRUE.equals(response);
}
@Override
public Operation getBackupOperation() {
return new TxnPutBackupOperation(name, dataKey, recordId, value);
}
@Override
protected void writeInternal(ObjectDataOutput out) throws IOException {
super.writeInternal(out);
out.writeLong(recordId);
IOUtil.writeData(out, value);
}
@Override
protected void readInternal(ObjectDataInput in) throws IOException {
super.readInternal(in);
recordId = in.readLong();
value = IOUtil.readData(in);
}
@Override
public int getClassId() {
return MultiMapDataSerializerHook.TXN_PUT;
}
}
| code |
विशेष खबर : मतदान खत्म होने के बाद खबर है कि मंगलवार को अमित शाह करेंगे एनडीए नेताओं के साथ डिनर - सीनियर जर्नलिस्ट पीयूष जैन
होम पॉलिटिक्स विशेष खबर : मतदान खत्म होने के बाद खबर है कि मंगलवार को अमित शाह करेंगे एनडीए नेताओं के साथ डिनर
नई दिल्ली। लोकसभा चुनाव के लिए मतदान खत्म हो चुका है और एग्जिट पोल्स में भाजपा नित सरकार भी बनती नजर आ रही है। हालांकि, सच्चाई का पता २३ मई को ही चलेगा जब मतगणना के बाद नतीजे आएंगे। इस बीच भाजपा के राष्ट्रीय अध्यक्ष अमित शाह ने मंगलवार शाम को एनडीए के नेताओं को डिनर पर बुलाया है। इस दौरान डिनर पर शाह सभी नेताओं से भविष्य की रणनीति पर चर्चा कर सकते हैं।
जानकारी के अनुसार, इस बैठक में राजग के सभी दलों के प्रमुख नेताओं के शामिल होने की उम्मीद जताई जा रही है। बता दें कि मतदान खत्म होने के बाद आए एग्जिट पोल्स में ज्यादातर नतीजे भाजाप नित राजग के पक्ष में जा रहे हैं और दूसरी बार मोदी सरकार की तरफ इशारा कर रहे हैं। इन एग्जिट पोल्स को लेकर जहां भाजपा में भारी उत्साह है वहीं विपक्षी दलों ने इन एग्जिट पोल्स को खारिज कर दिया है। | hindi |
वैष्णो देवी श्राइन बोर्ड को सर्वश्रेष्ठ स्वच्छ आइकोनिक स्थान पुरस्कार - मदगाय थे गवर्नमेंट जॉब आप्प
राष्ट्रपति रामनाथ कोविंद ने ६ सितम्बर २०१९ को नई दिल्ली में आयोजित एक कार्यक्रम में स्वच्छ भारत मिशन में असाधारण योगदान के लिए पुरस्कार प्रदान किये।
सर्वश्रेष्ठ स्वच्छ आइकोनिक स्थान:
जम्मू कश्मीर के वैष्णों देवी श्राइन बोर्ड को सर्वश्रेष्ठ स्वच्छ आइकोनिक स्थान पुरस्कार दिया गया। श्राइन बोर्ड को स्वच्छता में समग्र सुधार के आधार पर चुना गया था।
स्वच्छता कार्ययोजना श्रेणी:
रेल मंत्रालय को स्वच्छता कार्ययोजना श्रेणी में स्वच्छता पुरस्कार प्रदान किया गया।
स्वच्छता पखवाड़ा पुरस्कार:
रक्षा विभाग को स्वच्छता पखवाड़ा पुरस्कार दिया गया।
सार्वजनिक क्षेत्र के उपक्रम की श्रेणी में पुरस्कार:
पावर ग्रिड कारपोरेशन को सार्वजनिक क्षेत्र के उपक्रम की श्रेणी में पुरस्कार दिया गया।
ओडीएफ तथा व्यवहार परिवर्तन की श्रेणी में पुरस्कार:
गुजरात और सिक्किम को ओडीएफ तथा व्यवहार परिवर्तन की श्रेणी में पुरस्कार मिला।
भारतीय रेल को सर्वश्रेष्ठ मंत्रालय का पुरस्कार:
राष्ट्रपति श्री रामनाथ कोविंद ने २०१८-१९ के लिए स्वच्छता कार्य योजना के कार्यान्वयन के लिए भारतीय रेल को सर्वश्रेष्ठ मंत्रालय का पुरस्कार प्रदान किया। भारतीय रेल की ओर से रेलवे बोर्ड की चैयरमेन श्री विनोद कुमार यादव ने पुरस्कार प्राप्त किया।
राष्ट्रपति ने स्वच्छ भारत मिशन के तहत छत्रपति शिवाजी महाराज टर्मिनस (सीएसटी), मुंबई को सर्वश्रेष्ठ स्वच्छ प्रतिष्ठित स्थल का पुरस्कार प्रदान किया।
२०१८ के स्वच्छता सर्वेक्षण के तीन सबसे स्वच्छ स्टेशनों- जोधपुर, जयपुर और तिरुपति को भी पुरस्कार प्राप्त हुए।
श्री के. पारासरन को सर्वाधिक प्रतिष्ठित वरिष्ठ नागरिक पुरस्कार प्रदान किया गया
विश्व बांग्ला शरद सम्मान २०१९
बुकर पुरस्कार २०१९
संजीव नंदन सहाय को नया उर्जा सचिव नियुक्त किया गया
राष्ट्रपति ने साईं नो सातो में श्री सत्य साईं सनातन संस्कृति...
भारत में अपराध रिपोर्ट २०१७
पंकज कुमार बने उईदाई के नए सीईओ
सौरव गांगुली बने ब्क्सी के ३९वें अध्यक्ष
लक्ष्मीकांत मोहम्मद रफी लाइफटाइम अचीवमेंट अवार्ड से सम्मानित | hindi |
یۅس یٕہ بُلاک چین ٹؠکنٔولِجی منٛزیُس یٕہ بُلاکس چِھ آسن | kashmiri |
झालावाड़ में भी कोरोना की दस्तक / एक ही परिवार के ८ लोग पॉजिटिव मिले, इंदौर से संक्रमित होकर आने की आशंका डाग न्यूज
नगरपालिका क्षेत्र पिड़ावा के १५ वार्डों के २२०० घरों में १२८११ व्यक्तियों का सर्वे किया गया
इस परिवार में ४ दिन पहले एक महिला की हार्ट अटैक से मौत हो गई थी, जिनमें सर्दी जुकाम, बुखार के लक्षण थे
झालावाड़. कोरोना से अछूते चल रहे झालावाड़ पिछले २४ घंटे में ८ केस मिले। जिसमें गुरुवार सुबह ७ केस पॉजिटिव पाए गए। वहीं बुधवार रात एक केस सामने आया था। ये सभी केस झालावाड़ के पिड़ावा कस्बे में सामने आए हैं। जो एक ही परिवार के हैं। जिसके बाद मेडिकल स्टाफ सहित करीब १२० लोगों आइसोलेशन के लिए भेजे गए। इन मरीजों की इंदौर से संक्रमित होकर आने की आशंका है। इनमें से दो शादी की खरीदारी के लिए 1८ मार्च को इंदौर गए थे। पिड़ावा के आठ मरीजों की जांच रिपोर्ट पॉजिटिव आने के बाद पूरे नगरपालिका क्षेत्र में कर्फ्यू लगा दिया गया है। यह कर्फ्यू १५ अप्रैल रात १२ बजे तक रहेगा। संपूर्ण क्षेत्र को जीरो मोबिलिटी क्षेत्र घोषित किया गया है।
४ दिन पहले एक महिला की हार्ट अटैक से हुई थी मौत
पिड़ावा के दललेपुरा मोहल्ले में ४ दिन पहले एक महिला की मौत हो गई थी, हालांकि महिला की मौत का कारण हार्ट अटैक होना बताया गया था, लेकिन उसे भी सर्दी जुकाम, बुखार के लक्षण थे। साथ ही परिवार के अन्य लोगों में भी आसपास के लोगों ने यह लक्षण देखे थे। इसके बाद उन्होंने स्थानीय प्रशासन व चिकित्सा विभाग को सूचना दी। इसके बाद मेडिकल टीम और पुलिस सोमवार रात को दललेपुरा मोहल्ला पहुंची और चार जनों को स्थानीय अस्पताल लेकर आई। यहां जांच करने पर चारों को संदिग्ध मानते हुए उसी दिन झालावाड़ रैफर कर दिया गया। मंगलवार को झालावाड़ मेडिकल कॉलेज में चारों की कोरोना वायरस की स्क्रीनिंग जांच की गई। स्क्रीनिंग जांच में तीन जने कोरोना के संदिग्ध मिले। इस पर तीनों को कन्फर्मेट्री टेस्ट के लिए दुबारा सैंपल लेकर जयपुर भेजा गया। इसके बाद तीनों मरीजों को कोटा रैफर कर दिया गया। बुधवार को जयपुर से रिपोर्ट आने पर एक व्यक्ति पॉजिटिव मिला। गुरुवार सुबह ७ अन्य पॉजिटिव मिले।
पिड़ावा के २२०० घरों में १२८११ लोगों का सर्वे
नगरपालिका क्षेत्र पिड़ावा के १५ वार्डों के २२०० घरों में १२८११ व्यक्तियों का सर्वे किया गया। टीम में डॉक्टर व अन्य स्टाफ सहित ४१ मौजूद थे। सर्वे के पश्चात आने वाले सभी सर्वे टीम सदस्यों का सेनेटाइज किया गया तथा उनके द्वारा पहने गए ग्लब्स, मास्क, कैप, पीपीई किट को बायोमेडिकल वेस्ट की गाइड लाइन के अनुसार संकलित कर निस्तारण के लिए भिजवाए गए। सर्वे टीम एवं मैनेजमेंट संभालने वाले सभी को खाना खिलाने के बाद हाईड्रोक्सी क्लोरोक्विन गोली भी खिलवाई गई।
ट्रैवल हिस्ट्री : शादी की खरीदारी के लिए गए थे इंदौर
पिड़ावा में पॉजिटिव मिले मरीज की ट्रैवल हिस्ट्री सामने आई है। इसमें सामने आया है कि युवक के घर में २३ मार्च को शादी थी, इसकी खरीदारी के लिए १८ मार्च को इंदौर गए थे। इसी दौरान इनका एक रिश्तेदार कोटा से बारां-छबड़ा होता हुआ पिड़ावा आया था, वह भी संक्रमित था। इस कारण ये सभी इस वायरस से संक्रमित हो गए।
कर्फ्यू में लोग घरों में, चप्पे-चप्पे पर पुलिस
पिड़ावा में मंगलवार रात १२ बजे जिला प्रशासन द्वारा कर्फ्यू लगाने के बाद किसी भी व्यक्ति को बाहर निकलने की इजाजत नहीं है। इधर, कस्बे की सीमा से लेकर हर चौराहे पर पुलिस जवान तैनात रहे। डीएसपी धन्नाराम चौधरी, सीआई महेश सिंह ने कस्बे में राउंड लगाकर हालात का जायजा लिया। डीएसपी धन्नाराम ने बताया कि कस्बे में कानून व्यवस्था के लिए ८० पुलिसकर्मी तैनात किए गए हैं।
दूध के लिए लगानी पड़ी लाइनें
पिड़ावा कस्बे में कर्फ्यू लगने के बाद गुरुवार सुबह लोगों को दूध के लिए परेशानी उठानी पड़ी। दूध के लिए लोगों को लाइनों में लगना पड़ा। कहीं पर दूध पहुंचा तो कहीं पर लोग बिना दूध के रहे। हालांकि जिला प्रशासन ने सरस दूध की एक गाड़ी मंगवाई, लेकिन उसके वितरण में अव्यवस्था की सूचना के बाद एडीएम ने घर-घर जाकर दूध वितरण करवाने के निर्देश दिए। इसके बाद एक पटवारी रविन्द्र सिंह को व्यवस्था के लिए लगाया गया। हालांकि दूध आधा घंटा कस्बे में बंटा और खत्म हो गया। गलियों में रहने वाले लोगों को काफी मुसीबतों का सामना करना पड़ा।
कानून व्यवस्था के लिए ५ मजिस्ट्रेट नियुक्त
कस्बे में कानून व्यवस्था के लिए कलेक्टर ने ५ मजिस्ट्रेट नियुक्त किए हैं। तहसीलदार लक्ष्मीनारायण प्रजापत, बीडीओ ब्रजेश पराशर, नायब तहसीलदार रघुवीर स्वामी, सहायक उप वन संरक्षक दीपक गुप्ता व पीडब्ल्यूडी के एईएन सुनील सोनी को ड्यूटी मजिस्ट्रेट नियुक्त किया गया है।
पूरे पिड़ावा कस्बे में करवाया स्प्रे
नगरपालिका पिडावा की ओर से कोरोना संदिग्ध मरीज सामने आने के बाद पूरे नगरपालिका क्षेत्र के १५ वार्डों में सोडियम हाइपो क्लोराइड का स्प्रे करवाया गया। इसके लिए झालावाड़ से एक दमकल पिड़ावा के लिए भेजी गई। दमकल से पूरे कस्बे में स्प्रे करवाया गया।
प्रेवियस पोस्ट: राजस्थान में कोरोना के ४१३ मामले / ३० नए पॉजिटिव में झालावाड़ा, झुंझुनू और टोंक में ७-७ संक्रमित, बाड़मेर में भी पहला केस आया; एक की मौत
नेक्स्ट पोस्ट: #फाइट वित कोरोना / सलमान ने शेयर की शॉर्ट फिल्म वास्तव २, महेश और उनकी बेटी सई मांजरेकर ने घर में की शूटिंग | hindi |
// Dimensions of sunburst.
var width = 1500;
var height = 1000;
var radius = Math.min(width, height) / 2;
// Breadcrumb dimensions: width, height, spacing, width of tip/tail.
var b = {
w: 130, h: 30, s: 3, t: 10
};
// Mapping of step names to colors.
var color = d3.scale.category20c();
var colors = {
"home": "#5687d1",
"product": "#7b615c",
"search": "#de783b",
"account": "#6ab975",
"other": "#a173d1",
"end": "#bbbbbb"
};
// Total size of all segments; we set this later, after loading the data.
var totalSize = 0;
var vis = d3.select("#chart").append("svg:svg")
.attr("width", width)
.attr("height", height)
.append("svg:g")
.attr("id", "container")
.attr("transform", "translate(" + width / 2 + "," + height / 2 + ")");
var partition = d3.layout.partition()
.size([2 * Math.PI, radius * radius])
.value(function(d) { return d.size; });
var arc = d3.svg.arc()
.startAngle(function(d) { return d.x; })
.endAngle(function(d) { return d.x + d.dx; })
.innerRadius(function(d) { return Math.sqrt(d.y); })
.outerRadius(function(d) { return Math.sqrt(d.y + d.dy); });
// Use d3.text and d3.csv.parseRows so that we do not need to have a header
// row, and can receive the csv as an array of arrays.
d3.json("taxonomy.json", function(json) {
// var csv = d3.csv.parseRows(text);
// var json = buildHierarchy(text);
createVisualization(json);
});
// Main function to draw and set up the visualization, once we have the data.
function createVisualization(json) {
// Basic setup of page elements.
initializeBreadcrumbTrail();
// drawLegend();
// d3.select("#togglelegend").on("click", toggleLegend);
// Bounding circle underneath the sunburst, to make it easier to detect
// when the mouse leaves the parent g.
vis.append("svg:circle")
.attr("r", radius)
.style("opacity", 0);
// For efficiency, filter nodes to keep only those large enough to see.
var nodes = partition.nodes(json)
.filter(function(d) {
return (d.dx > 0.005); // 0.005 radians = 0.29 degrees
});
var path = vis.data([json]).selectAll("path")
.data(nodes)
.enter().append("svg:path")
.attr("display", function(d) { return d.depth ? null : "none"; })
.attr("d", arc)
.attr("fill-rule", "evenodd")
.style("fill", function(d) { return color((d.children ? d : d.parent).name); })
.style("opacity", 1)
.on("mouseover", mouseover);
// Add the mouseleave handler to the bounding circle.
d3.select("#container").on("mouseleave", mouseleave);
// Get total size of the tree = value of root node from partition.
totalSize = path.node().__data__.value;
};
// Fade all but the current sequence, and show it in the breadcrumb trail.
function mouseover(d) {
var percentage = (100 * d.value / totalSize).toPrecision(3);
var percentageString = percentage + "%";
if (percentage < 0.1) {
percentageString = "< 0.1%";
}
d3.select("#percentage")
.text(percentageString);
d3.select("#explanation")
.style("visibility", "");
var sequenceArray = getAncestors(d);
updateBreadcrumbs(sequenceArray, percentageString);
// Fade all the segments.
d3.selectAll("path")
.style("opacity", 0.3);
// Then highlight only those that are an ancestor of the current segment.
vis.selectAll("path")
.filter(function(node) {
return (sequenceArray.indexOf(node) >= 0);
})
.style("opacity", 1);
}
// Restore everything to full opacity when moving off the visualization.
function mouseleave(d) {
// Hide the breadcrumb trail
d3.select("#trail")
.style("visibility", "hidden");
// Deactivate all segments during transition.
d3.selectAll("path").on("mouseover", null);
// Transition each segment to full opacity and then reactivate it.
d3.selectAll("path")
.transition()
.duration(1000)
.style("opacity", 1)
.each("end", function() {
d3.select(this).on("mouseover", mouseover);
});
d3.select("#explanation")
.style("visibility", "hidden");
}
// Given a node in a partition layout, return an array of all of its ancestor
// nodes, highest first, but excluding the root.
function getAncestors(node) {
var path = [];
var current = node;
while (current.parent) {
path.unshift(current);
current = current.parent;
}
return path;
}
function initializeBreadcrumbTrail() {
// Add the svg area.
var trail = d3.select("#sequence").append("svg:svg")
.attr("width", width)
.attr("height", 50)
.attr("id", "trail");
// Add the label at the end, for the percentage.
trail.append("svg:text")
.attr("id", "endlabel")
.style("fill", "#000");
}
// Generate a string that describes the points of a breadcrumb polygon.
function breadcrumbPoints(d, i) {
var points = [];
points.push("0,0");
points.push(b.w + ",0");
points.push(b.w + b.t + "," + (b.h / 2));
points.push(b.w + "," + b.h);
points.push("0," + b.h);
if (i > 0) { // Leftmost breadcrumb; don't include 6th vertex.
points.push(b.t + "," + (b.h / 2));
}
return points.join(" ");
}
// Update the breadcrumb trail to show the current sequence and percentage.
function updateBreadcrumbs(nodeArray, percentageString) {
// Data join; key function combines name and depth (= position in sequence).
var g = d3.select("#trail")
.selectAll("g")
.data(nodeArray, function(d) { return d.name + d.depth; });
// Add breadcrumb and label for entering nodes.
var entering = g.enter().append("svg:g");
entering.append("svg:polygon")
.attr("points", breadcrumbPoints)
.style("fill", function(d) { return color((d.children ? d : d.parent).name); });
entering.append("svg:text")
.attr("x", (b.w + b.t) / 2)
.attr("y", b.h / 2)
.attr("dy", "0.35em")
.attr("text-anchor", "middle")
.text(function(d) { return d.name; });
// Set position for entering and updating nodes.
g.attr("transform", function(d, i) {
return "translate(" + i * (b.w + b.s) + ", 0)";
});
// Remove exiting nodes.
g.exit().remove();
// Now move and update the percentage at the end.
d3.select("#trail").select("#endlabel")
.attr("x", (nodeArray.length + 0.5) * (b.w + b.s))
.attr("y", b.h / 2)
.attr("dy", "0.35em")
.attr("text-anchor", "middle")
.text(percentageString);
// Make the breadcrumb trail visible, if it's hidden.
d3.select("#trail")
.style("visibility", "");
}
function drawLegend() {
// Dimensions of legend item: width, height, spacing, radius of rounded rect.
var li = {
w: 75, h: 30, s: 3, r: 3
};
var legend = d3.select("#legend").append("svg:svg")
.attr("width", li.w)
.attr("height", d3.keys(colors).length * (li.h + li.s));
var g = legend.selectAll("g")
.data(d3.entries(colors))
.enter().append("svg:g")
.attr("transform", function(d, i) {
return "translate(0," + i * (li.h + li.s) + ")";
});
g.append("svg:rect")
.attr("rx", li.r)
.attr("ry", li.r)
.attr("width", li.w)
.attr("height", li.h)
.style("fill", function(d) { return d.value; });
g.append("svg:text")
.attr("x", li.w / 2)
.attr("y", li.h / 2)
.attr("dy", "0.35em")
.attr("text-anchor", "middle")
.text(function(d) { return d.key; });
}
function toggleLegend() {
var legend = d3.select("#legend");
if (legend.style("visibility") == "hidden") {
legend.style("visibility", "");
} else {
legend.style("visibility", "hidden");
}
}
// Take a 2-column CSV and transform it into a hierarchical structure suitable
// for a partition layout. The first column is a sequence of step names, from
// root to leaf, separated by hyphens. The second column is a count of how
// often that sequence occurred.
function buildHierarchy(csv) {
var root = {"name": "root", "children": []};
for (var i = 0; i < csv.length; i++) {
var sequence = csv[i][0];
var size = +csv[i][1];
if (isNaN(size)) { // e.g. if this is a header row
continue;
}
var parts = sequence.split("-");
var currentNode = root;
for (var j = 0; j < parts.length; j++) {
var children = currentNode["children"];
var nodeName = parts[j];
var childNode;
if (j + 1 < parts.length) {
// Not yet at the end of the sequence; move down the tree.
var foundChild = false;
for (var k = 0; k < children.length; k++) {
if (children[k]["name"] == nodeName) {
childNode = children[k];
foundChild = true;
break;
}
}
// If we don't already have a child node for this branch, create it.
if (!foundChild) {
childNode = {"name": nodeName, "children": []};
children.push(childNode);
}
currentNode = childNode;
} else {
// Reached the end of the sequence; create a leaf node.
childNode = {"name": nodeName, "size": size};
children.push(childNode);
}
}
}
return root;
};
| code |
Digital Generalists - Digital Generalists offers website creation, design, and application development services from our Denver, Colorado headquarters.
Crafting a digital presence requires a set of interconnected skills. Digital Generalists has the competencies needed to help you navigate the internet’s varied landscape. We develop custom mobile and web applications, consult on branding, and offer a broad range of design skills. | english |
<?php
namespace IMI\Contao\Command\Developer\Module\Rewrite;
use IMI\Contao\Command\AbstractContaoCommand;
use Symfony\Component\Finder\Finder;
abstract class AbstractRewriteCommand extends AbstractContaoCommand
{
protected $_rewriteTypes = array(
'blocks',
'helpers',
'models',
);
/**
* Return all rewrites
*
* @return array
*/
protected function loadRewrites()
{
$return = array(
'blocks',
'models',
'helpers',
);
// Load config of each module because modules can overwrite config each other. Globl config is already merged
$modules = \Mage::getConfig()->getNode('modules')->children();
foreach ($modules as $moduleName => $moduleData) {
// Check only active modules
if (!$moduleData->is('active')) {
continue;
}
// Load config of module
$configXmlFile = \Mage::getConfig()->getModuleDir('etc', $moduleName) . DIRECTORY_SEPARATOR . 'config.xml';
if (! file_exists($configXmlFile)) {
continue;
}
$xml = \simplexml_load_file($configXmlFile);
if ($xml) {
$rewriteElements = $xml->xpath('//rewrite');
foreach ($rewriteElements as $element) {
foreach ($element->children() as $child) {
$type = \simplexml_import_dom(dom_import_simplexml($element)->parentNode->parentNode)->getName();
if (!in_array($type, $this->_rewriteTypes)) {
continue;
}
$groupClassName = \simplexml_import_dom(dom_import_simplexml($element)->parentNode)->getName();
if (!isset($return[$type][$groupClassName . '/' . $child->getName()])) {
$return[$type][$groupClassName . '/' . $child->getName()] = array();
}
$return[$type][$groupClassName . '/' . $child->getName()][] = (string) $child;
}
}
}
}
return $return;
}
/**
* Check codepools for core overwrites.
*
* @return array
*/
protected function loadAutoloaderRewrites()
{
$return = $this->loadAutoloaderRewritesByCodepool('community');
$return = array_merge($return, $this->loadAutoloaderRewritesByCodepool('local'));
return $return;
}
/**
* Searches for all rewrites over autoloader in "app/code/<codepool>" of
* Mage, Enterprise Zend, Varien namespaces.
*
* @param string $codePool
* @return array
*/
protected function loadAutoloaderRewritesByCodepool($codePool)
{
$return = array();
$localCodeFolder = \Mage::getBaseDir('code') . '/' . $codePool;
$folders = array(
'Mage' => $localCodeFolder . '/Mage',
'Enterprise' => $localCodeFolder . '/Enterprise',
'Varien' => $localCodeFolder . '/Varien',
'Zend' => $localCodeFolder . '/Zend',
);
foreach ($folders as $vendorPrefix => $folder) {
if (is_dir($folder)) {
$finder = new Finder();
$finder
->files()
->ignoreUnreadableDirs(true)
->followLinks()
->in($folder);
foreach ($finder as $file) {
$classFile = trim(str_replace($folder, '', $file->getPathname()), '/');
$className = $vendorPrefix
. '_'
. str_replace(DIRECTORY_SEPARATOR, '_', $classFile);
$className = substr($className, 0, -4); // replace .php extension
$return['autoload: ' . $vendorPrefix][$className][] = $className;
}
}
}
return $return;
}
} | code |
\begin{document}
\subjclass[2020]{Primary 54F15; Secondary 54F16}
\title{Some theorems on colocally connected continua }
\begin{abstract}
We show that each refinable map preserves colocal connectedness of the domain while a proximately refinable map does not necessarily. Also, we prove that colocal connectedness is a Whitney property and is not a Whitney reversible property.
\end{abstract}
\section{Introduction}
In this paper, unless otherwise stated, all spaces are assumed to be metrizable. When we use the term $function$, we do not assume it to be continuous necessarily while we require $map$ to be continuous.
Let $X$ be a continuum and $x \in X$. We say that $X$ is {\it colocally connected} if for each $x \in X$ and each neighborhood $V \subseteq X$ of $x$, there exists an open neighborhood $U \subseteq X$ of $x$ such that $x \in U \subseteq V$ and $X \setminus U$ is connected. A continuum $X$ is said be $aposyndetic$ if for any two distinct points $x,y \in X$, there exists a subcontinuum $T \subseteq X$ such that $x \in {\rm Int}_X T \subseteq T \subseteq X \setminus \{y\}$, where ${\rm Int}_X T$ denotes the interior of $T$ in $X$. Jones introduced aposyndetic continua in \mathcal{CI}te{jonesap}. Since then, aposyndetic continua have been studied for many years.
It is known that every colocally connected continuum is aposyndetic \mathcal{CI}te[Remark 5.4.15]{macias}.
As the consequence, colocal connectedness implies many properties of continua (see \mathcal{CI}te[Figure 6]{D}. See also \mathcal{CI}te[p.239]{bobok} for other properties derived from colocal connectedness).
If $(X,d)$ is a space and $A \subseteq X$, then we denote ${\rm sup}\{d(a,b) \ | \ a,b \in A \}$ by ${\rm diam}_d A$. Let $(X,d_X)$ and $(Y,d_Y)$ be continua and let $\varepsilon > 0$. A surjective map $f: X \to Y$ is called an $\varepsilon$-$map$ if for each $y \in Y$, ${\rm diam}_{d_X} f^{-1}(y) < \varepsilon$. If $g, ~ g_{\varepsilon} : X \to Y$ are surjective maps such that $g_{\varepsilon}$ is an $\varepsilon$-map and $d_Y(g(x), g_{\varepsilon}(x)) < \varepsilon$ for each $x \in X$, then $g_{\varepsilon}$ is called an $\varepsilon$-$refinement$ $of$ $g$. A surjective map $r : X \to Y$ is called a $refinable ~ map$ if for each $\varepsilon > 0$, there exists an $\varepsilon$-refinement $r_{\varepsilon} : X \to Y$ of $r$. The notion of a refinable map was introduced in \mathcal{CI}te{ford}.
If $X$ is
a continuum, then we denote the space of all nonempty subcontinua of $X$ endowed with the Hausdorff metric by $C(X)$. $C(X)$ is called the $hyperspace$ $of$ $X$. A $Whitney$
$map$ is a map $\mu : C(X) \to [0,\mu(X)]$ satisfying $\mu(\{x\})=0$ for each $x \in X$ and $\mu(A) < \mu(B)$ whenever $A, B \in C(X)$ and $A \subsetneq B$. It is well-known that for each Whitney map $\mu: C(X) \to [0,\mu(X)]$
and each $t \in [0, \mu(X)]$, $\mu^{-1}(t)$ is a continuum (\mathcal{CI}te[Theorem 19.9]{illanes}).
A topological property $P$ is called a {\it Whitney property} if a continuum $X$ has property $P$, so does $\mu^{-1}(t)$ for each Whitney map $\mu$ for $C(X)$ and each $t \in [0, \mu(X))$. Also, a topological property $P$ is called a {\it Whitney reversible property} provided that whenever $X$ is a continuum such that $\mu^{-1}(t)$ has property $P$ for each Whitney map $\mu$ for $C(X)$ and {for} each $t \in (0, \mu(X))$, then $X$ has property $P$. Many researchers have studied these properties so far. As for information about Whitney properties and Whitney reversible properties, for example, see \mathcal{CI}te[Chapter 8]{illanes}.
In \mathcal{CI}te{hosokawa}, Hosokawa proved that each refinable map defined on a continuum preserves aposyndesis. Also, in \mathcal{CI}te{petrus} Petrus proved that aposyndesis is a Whitney property and is not a Whitney reversible property. In this paper, we show that each refinable map preserves colocal connectedness of the domain while a proximately refinable map does not necessarily (for the definition of a proximately refinable map, see section 2). Also, we prove that colocal connectedness is a Whitney property and is not a Whitney reversible property.
\section{refinable maps and proximately refinable maps defined on colocally connected continua}
In this section, we deal with topics on refinable maps. First, we show an
example of a refinable map between colocally connected continua which is not a homeomorphism.
\begin{example}
Take a continuum $X$ and a refinable map $f : X \to f(X)$ such that $X$ and $f(X)$ are not homeomorphic (for an example of a refinable map which is not a homeomorphism, see \mathcal{CI}te{ford}). Let $Y$ be a nondegenerate continuum. By \mathcal{CI}te[Lemma 3.5]{loncar3}, $X \times Y$ and $f(X) \times Y$ are colocally connected. Then, a map $F : X \times Y \to f(X) \times Y ; (x,y) \mapsto (f(x),y)$ is a refinable map which is not a homeomorphism.
\end{example}
The following theorem is the main result in this section.
Before the theorem, we give a notation. If $X$ is a space and $A \subset X$, then ${\rm Cl}_X A$ denotes the closure of $A$ in $X$.
\begin{theorem}
Let $(X,d_X)$ and $(Y,d_Y)$ be continua and let $f : X \to Y$ be a refinable map. If $X$ is colocally connected, then so is $Y$.
\label{refinableco}
\end{theorem}
\begin{proof}
Let $y \in Y$ and let $V \subseteq Y$ be an open neighborhood of $y$. Since $f$ is a refinable map, there exists a sequence $\{f_{\frac{1}{n}}\}_{n=1}^{\infty}$ of $\frac{1}{n}$-refinements of $f$. We may assume that $\lim f_{\frac{1}{n}}^{-1}(y)$ exists. Let $\lim f_{\frac{1}{n}}^{-1}(y)=\{x\}$. Then, it is easy to see that $x \in f^{-1}(y)$. Since $X$ is colocally connected, there exists an open neighborhood $B \subseteq X$ of $x$ such that $x \in B \subseteq {\rm Cl}_X B \subseteq f^{-1}(V)$ and $X \setminus B$ is connected. Let $\delta = {\rm inf} \{d_Y(b,c) \ | \ b \in f({\rm Cl}_X B), \ c \in Y \setminus V \}$. Then, there exists $n_0 \in \mathbb{N}$ such that $f_{\frac{1}{n_0}}^{-1}(y) \subseteq B$ and $d_Y(f(x), f_{\frac{1}{n_0}}(x)) < \frac{\delta}{2}$ for each $x \in X$. Let $U=Y \setminus f_{\frac{1}{n_0}}(X \setminus B)$. Then, we see that $Y \setminus U=f_{\frac{1}{n_0}}(X \setminus B)$ is connected and $y \in U \subseteq f_{\frac{1}{n_0}}( {\rm Cl}_X B) \subseteq V$. Therefore, we see that $Y$ is colocally connected. \end{proof}
A continuum is said to be $semilocally ~ connected$ if for each $x \in X$ and each neighborhood $V \subseteq X$ of $x$ there exists an open neighborhood $U \subseteq X$ of $x$ such that $x \in U \subseteq V$ and $X \setminus U$ has finitely many components.
\begin{theorem}
Let $X$ and $Y$ be continua and let $f : X \to Y$ be a refinable map. If $X$ is semilocally connected, then so is $Y$. \label{refinablesemi}
\end{theorem}
\begin{proof}
The proof is similar to the proof of the previous result. In fact, change the proof of Theorem \ref{refinableco} as follows:
$\bullet$ In the proof of Theorem \ref{refinableco}, we took an open neighborhood $B \subseteq X$ of $x$ such that $X \setminus B$ is connected. Instead of it, take an open neighborhood $B \subseteq X$ of $x$ such that $X \setminus B$ has finitely many components.
$\bullet$ Also, in the same proof, we stated that $Y \setminus U$ is connected. However, by taking $B$ as above, we can easily see that $Y \setminus U$ has finitely many components.
By these two remarks, we can prove Theorem \ref{refinablesemi}. \end{proof}
It is known that a continuum $X$ is aposydetic if and only if $X$ is semilocally connected (see \mathcal{CI}te{jonesap}). Hence, Theorem \ref{refinablesemi} implies the following result proven by Hosokawa \mathcal{CI}te{hosokawa} and vice versa.
\begin{theorem}{\rm (\mathcal{CI}te[Corollary (p.368)]{hosokawa})}
Let $X$ and $Y$ be continua and let $f : X \to Y$ be a refinable map. If $X$ is aposyndetic, then so is $Y$.
\end{theorem}
If $(X,d)$ is a space, $x \in X$ and $\varepsilon > 0$, then we denote the set $\{ y \in X \ | \ d(x,y) < \varepsilon\}$ by $U_d(x,\varepsilon)$.
A function $f: (X,d_X) \to (Y,d_Y)$ between spaces is said to be $\varepsilon$-$continuous$ if for each
$x \in X$ there exists an open neighborhood $U \subset X$ of $x$ such that $f(U) \subseteq U_{d_Y}(f(x), \varepsilon)$. A surjective function $g:(X,d_X) \to (Y,d_Y)$ is called a {\it strong $\varepsilon$-function} if for each $y \in Y$, there exists an open neighborhood $V \subseteq Y$ of $y$ such that ${\rm diam}_{d_X} g^{-1}(V) < \varepsilon$.
Let $f:(X,d_X) \to (Y,d_Y)$ be a surjective function between continua.
A surjective
function $g: X \to Y$ is called a {\it proximate $\varepsilon$-refinement of $f$}
if $g$ is $\varepsilon$-continuous, $g$ is a strong $\varepsilon$-function
and $d_Y(f(x), g(x)) < \varepsilon$ for each $x \in X$.
A surjective function $p: X \to Y$ is said to be {\it proximately refinable}
if for any $\varepsilon > 0$ there exists a proximate $\varepsilon$-refinement of $p$. We can easily see that every proximately refinable function is a map. The notion of a proximately refinable map was introduced in \mathcal{CI}te{grace}.
The following result was proven by Grace and Vought in \mathcal{CI}te{grace2}.
\begin{theorem}{\rm (\mathcal{CI}te[Theorem 2]{grace2})}
A surjective map defined on a graph is proximately refinable if and only if it is monotone.
\label{proximate}
\end{theorem}
By the following example, we see that a proximately refinable map does not preserve colocal connectedness of the domain necessarily. Before the example, we give a notation. If $X$ is a space and $A \subset X$, then ${\rm Bd}_X A$ denotes the boundary of $A$ in $X$.
\begin{example}
Let $X$ be the subcontinuum in $\mathbb{R}^2$ defined by $X = {\rm Bd}_{\mathbb{R}^2} [0,1]^2 \cup \{(\frac{1}{2},y) \ | \ 0 \le y \le 1\}$. Let $Y$ be the quotient space obtained from $X$ by shrinking $\{(\frac{1}{2},y) \ | \ 0 \le y \le 1\} $ to the
point and let $f : X \to Y$ be the quotient map. Then, it is easy to see that $f$ is a surjective monotone map, $X$ is a colocally connected graph, and $Y$ is not colocally connected. By Theorem \ref{proximate}, $f$ is proximately refinable. Hence, colocal connectedness of the domain is not necessarily preserved by a proximately refinable map.
\end{example}
\section{A Whitney property and a Whitney reversible property}
Let $X$ be a continuum and $p \in X$. We say that $p$ is a $weak$ $cut$ $point$ $of$ $X$ if there exist distinct points $x,y \in X \setminus \{p\}$ such that for each subcontinuum $C \subseteq X$ with $x,y \in C$, $p \in C$. If a point of $X$ is not a weak cut point, then the point is called a $non$-$weak$ $cut$ $point$. It is easy to see that if a continuum $X$ is colocally connected, then $X$ is a continuum having only non-weak cut points.
As mentioned earlier, aposyndesis is a Whitney property and is not a Whitney reversible property. Also, it is known that the property of having only non-weak cut points is a Whitney property and is not a Whitney reversible property (\mathcal{CI}te[Theorem 2.3 and Theorem 2.10]{bautista}). In this section, we prove that colocal connectedness is a Whitney property and is not a Whitney reversible property.
The main aim of this section is to prove Theorem \ref{whitneyproperty}. To prove the theorem, we need Lemma \ref{exe}. Before stating those results, we give notation. If $(X,d)$ is a continuum and $A$ is a closed subset of $X$, then we denote the set $\{x \in X \ | \ {\rm there \ exists }\ a \in A \ {\rm such \ that } \ d(x,a) < \varepsilon \}$ by $N_d(A, \varepsilon)$. Also, $H_d$ denotes the Hausdorff metric on $C(X)$ induced by $d$. Finally, if $\mathcal{A}$ is a family of subsets of $X$, then we denote ${\rm sup} \{{\rm diam}_d A \ | \ A \in \mathcal{A}\}$ by mesh$_d\mathcal{A}$.
\begin{lemma}{\rm(\mathcal{CI}te[Exercise 4.33 (b)]{nadler1})}
Let $(X,d)$ be a continuum and let $\mu : C(X) \to [0, \mu(X)]$ be a Whitney map. Then, for each $\varepsilon > 0$, there exists $\delta > 0$ such that if $A,B \in C(X)$ satisfy $B \subseteq N_d(A, \delta)$ and $|\mu(A) - \mu(B)| < \delta$, then $H_d(A,B) < \varepsilon$.
\label{exe}
\end{lemma}
\begin{theorem}
Colocal connectedness is a Whitney property.
\label{whitneyproperty}
\end{theorem}
\begin{proof}
Let $(X,d)$ be a colocally connected continuum, let $\mu: C(X) \to [0,\mu(X)]$ be a Whitney map and let $t \in (0,\mu(X))$. Let $A \in \mu^{-1}(t)$ and let $\varepsilon > 0$. We will find an open neighborhood $\mathcal{O} \subseteq \mu^{-1}(t)$ of $A$ such that $\mathcal{O} \subseteq U_{H_d}(A, \varepsilon)$ and $\mu^{-1}(t) \setminus \mathcal{O}$ is connected.
Take $\delta > 0$ as in the statement of Lemma \ref{exe}. Since $X$ is colocally connected, for each $a \in A$, there exists an open neighborhood $O_a \subset X$ such that ${\rm diam}_d O_a < \delta$, $X \setminus O_a$ is connected and $\mu(X \setminus O_a) > t$. Then, $\{O_a\}_{a \in A}$ covers $A$. Also, since $X$ is colocally connected and $A$ is compact, we can find a finite collection $\mathcal{H}=\{H_i\}_{i=1}^n$ of open subsets of $X$ such that
(1) $\mathcal{H}$ covers $A$,
(2) for each $i=1,2,\ldots,n$, $A \cap H_i \neq \emptyset$,
(3) for each $i=1,2,\ldots,n$, $X \setminus H_i$ is connected, and
(4) if $H, H' \in \mathcal{H}$ and $H \cap H' \neq \emptyset$, then there exists $a \in A$ such that $H \cup H' \subseteq O_a$.
We may assume that if $H_i, H_j \in \mathcal{H}$ and $|i-j| \le 1$, then $H_i \cap H_j \neq \emptyset$. In this case, note that it is possible $H_i=H_j$ despite $i \neq j$. For each $i=1,2,\ldots,n$, let $\mathcal{H}_i = \{C \in \mu^{-1}(t) \ |\ C \subseteq X \setminus H_i\}$. Now, we show the following:
\begin{itemize}
\item[$\bullet$] $\bigcup_{i=1}^n \mathcal{H}_i$ is a subcontinuum of $\mu^{-1}(t)$.
\end{itemize}
First, by \mathcal{CI}te[Exercise 27.7]{illanes}, each $\mathcal{H}_i$ is a subcontinuum of $\mu^{-1}(t)$ (note that each $\mathcal{H}_i$ is nonempty by the fact that $\mu(X \setminus O_a)>t$ for each $a \in A$ and \mathcal{CI}te[Theorem 14.6]{illanes}). Hence, it is enough to show that $\mathcal{H}_i \cap \mathcal{H}_{i+1} \neq \emptyset$ for each $i=1,2,\ldots,n-1$. Let $i=1,2.\ldots,n-1$. Since $H_i \cap H_{i+1} \neq \emptyset$, there exists $a \in A$ such that $H_i \cup H_{i+1} \subseteq O_a$. Since $\mu(X \setminus O_a)>t,$ by \mathcal{CI}te[Theorem 14.6]{illanes} we see that there exists a subcontinuum $K \subseteq X \setminus O_a$ such that $\mu(K)=t$. Note that $K \in \mathcal{H}_i \cap \mathcal{H}_{i+1}$. Therefore, we see that $\bigcup_{i=1}^n \mathcal{H}_i$ is a continuum.
Let $\mathcal{O}= \mu^{-1}(t) \setminus \bigcup_{i=1}^n \mathcal{H}_i$. By the above argument, $\mu^{-1}(t) \setminus \mathcal{O} = \bigcup_{i=1}^n \mathcal{H}_i$ is connected. Also, by (2), it follows that $A \notin \bigcup_{i=1}^n \mathcal{H}_i$. Therefore, $A \in \mathcal{O}$. Thus, $\mathcal{O} \subseteq \mu^{-1}(t)$ is an open neighborhood of $A$. Finally, we show that $ \mathcal{O} \subseteq U_{H_d}(A, \varepsilon)$. Let $B \in \mathcal{O}$. Then, $B \notin \bigcup_{i=1}^n \mathcal{H}_i$. Hence, for each $i=1,2,...,n$, $B \cap H_i \neq \emptyset$. Since $\mathcal{H}$ covers $A$ and ${\rm mesh}_d \mathcal{H} < \delta$, it follows that $A \subseteq N_d(B,\delta)$. Note that $\mu(A)=\mu(B)=t$. Hence, by Lemma \ref{exe}, we see that $H_d(A,B) < \varepsilon$. Therefore, $\mathcal{O} \subseteq U_{H_d}(A, \varepsilon)$.
Thus, we see that $\mu^{-1}(t)$ is colocally connected. This completes the proof. \end{proof}
The following example is appeared in \mathcal{CI}te[Example 2.10]{bautista} to show that the property of having only non-weak cut points is not a Whitney reversible property. By the same example, we see that colocal connectedness is not a Whitney reversible property.
\begin{example}{\rm (cf. \mathcal{CI}te[Example 2.10]{bautista})}
Let $X$ be a dendrite whose branch points are dense in $X$ and let $\mu : C(X) \to [0,\mu(X)]$ be a Whitney map. By \mathcal{CI}te[Theorem 4.8]{good}, for each $t \in (0, \mu(X))$, $\mu^{-1}(t)$ is homeomorphic to the Hilbert cube. Hence, $\mu^{-1}(t)$ is colocally connected for each $t \in (0, \mu(X))$. Since $X$ is a dendrite, $X$ is not colocally connected. Therefore, we see that colocal connectedness is not a Whitney reversible property.
\end{example}
\end{document} | math |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.